应用地脉动的三维速度结构进行数值建模的研究

陈运飞

（北京市路政局道路建设工程项目管理中心，北京100031）

·岩土工程·

应用地脉动的三维速度结构进行数值建模的研究

陈运飞*

（北京市路政局道路建设工程项目管理中心，北京100031）

进行数值模拟的前提就是具备一个良好的数值模型，好的三维模型不仅仅要与真实的地理地质情况相匹配，而且还需要具有一定的平滑度。建模的关键在于确定目标区内各控制点所对应的各物理层或地质层的深度。另外，也需要确定各层对应的介质物理力学参数。提出以地脉动实测值为目标函数，通过调整模型与介质物理力学参数，拟合地脉动实测点解析波谱，从而确定数值模型的方法，为数值模拟建模提供了一条新思路。最后结合宝鸡市长寿沟黄土边坡的建模实例，应用地脉动的三维速度结构进行了建模尝试，拓展了地脉动的应用空间。

地脉动；数值建模；解析波谱；拟合

岩土力学数值模拟中，模型的正确建立与介质物理力学参数的合理选取对于整个模拟结果的准确性起着至关重要的作用，否则进行数值模拟的结果只能是“垃圾进，垃圾出”［1］。好的三维模型不仅仅要与真实的地理地质模型相匹配，而且还需要具有一定的平滑度（由于大量的科学计算的要求）［2］。然而，由于岩土体的复杂性，在进行数值模拟的过程中，合理力学模型的建立往往是非常困难的一个环节。利用地脉动观测和数据解析来推断地下构造一直作为一种可靠有效、方便快捷的方法，在国外（尤其是日本）广泛应用于各个城市的抗震减灾工作中。

1　地脉动及用其于建模的理论性研究

1.1地脉动研究概况

地脉动（micro tremors）是一种稳定的非重复性的空间随机波场，简单地将其看作一时间域的平稳随机过程，蕴涵了大量的、丰富的地球物理信息［3］。地脉动的频谱特性既能反映场地土层特征，又能反映工程场地的动力特性，在工程场地地震安全评价和地震小区划、场地类别的划分、场地选择和评价等工作中有广泛的应用［4］。

本文所提出的新的建模方法，即以地脉动为实测值为目标函数，通过调整模型与介质物理力学参数，拟合地脉动实测点解析波谱，从而确定数值模型的方法，是一种尝试性的方法。

1.2应用地脉动建模的方法体系和具体步骤

1.2.1应用地脉动频谱特性进行数值建模的具体的方法体系

（1）数值模型的初建。利用物探资料、地质资料和地理资料确定目标区各物理层的地下分层情况及各层的深度，以及确定目标区内任意一点所对应的各层的深度值。

根据场地基本周期估算公式：

式中：T——场地的卓越周期，s；

hi——第i层土的厚度，m；

vsi——第i层土的横波波速，m/s；

i——土层数。

对场地的基本周期进行粗略估计，保证理论基本周期值与实测解析波谱基本周期值大致吻合，初步建立边坡的初始三维数值模型，由于占有的地理地质资料的有限性及对该三维数值模型进行了较大程度的概化，因而初建的三维数值模型将十分粗略，而且常常会出现突兀点。这就需要利用地脉动的数据进行不断的修改和完善。

（2）地脉动数据的应用。在利用地脉动观测结果时，每一个观测点都对应有各层的深度值。根据前面提到的反演计算方法，对每个测点进行反演计算，将反演的理论计算值Tt与相应点解析波谱的卓越周期Tm进行比较，观察其卓越周期是否一致。如果一致，则说明已经建立的数值模型上该点对应的各层深度值及介质物理力学参数是合理的，反之，需要对数值模型进行比例粗调或微调模型的深度值，或者对模型介质物理力学参数进行调整，重新反演，一直使其理论计算卓越周期与该点的地脉动解析波谱所对应的卓越周期一致。至此，数值模型及介质物理力学参数初步确定。

（3）地脉动观测点解析波谱的拟合。采用已建立的边坡初始模型及介质物理力学参数，以一系列频率不同、振动强度相同的微振荷载激励模型，使边坡数值模型进入弹性微振状态，监测数值模型上地脉动实测点相应测点的波谱，与实测解析波谱进行比较，观察其卓越周期是否一致，如果不一致，可以通过调整激励大小或者再次调整初始数值模型介质物理力学参数实现。

地脉动不同测点的观测解析波谱实质上为数值模型的合理建立提供了一系列的物理约束条件，数值模型对实测地脉动的拟合过程，就是模型介质的调参过程。必须要通过假设—修改—再假设这个反复的过程，直到每一个观测点全部拟合上，从而建立完整的三维速度结构数值模型。

1.2.2具体步骤（见流程图1）

图1　应用地脉动三维速度结构进行建模流程图

2　建模实例

2.1初建三维模型

长寿沟黄土边坡位于宝鸡市金河乡朱家崖村东部，地理坐标为东经107°06′，北纬34°24′。地脉动测试长寿沟测线为近东西向布设，工作区取为东经107°06′15″～107°06′26″，北纬34°24′07″～34°24′07″。共布设测点5处，编号分别为D5-1、D5-2、D5-3、D5-4、D5-5。如图2所示。

该测线所在地形为由东向西逐渐抬升的单面缓坡黄土塬地形，随着地形的抬升，覆盖层厚度也呈逐渐加厚趋势。根据该边坡岩土勘察试验，长寿沟黄土边坡物理力学参数见表1。

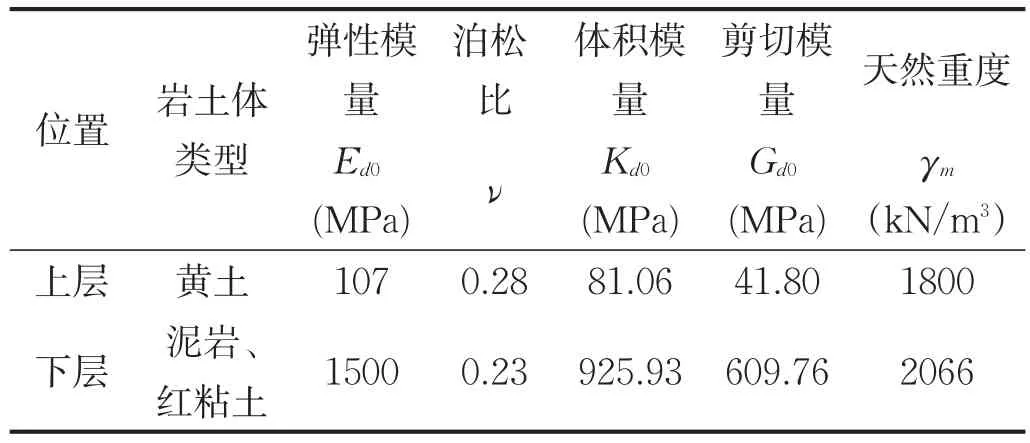
表1　长寿沟黄土边坡物理力学参数表

根据地理、地质资料，并依据场地卓越周期估算的结果，粗略建立以下初始模型。见图3。

2.2地脉动波谱拟合

为实现对现场实测地脉动过程的拟合，首先参考边坡岩土勘察试验得到的岩土物理力学参数，为边坡数值模型赋与初值。以一系列频率不同、振动强度相同的微振荷载激励模型，使边坡模型进入弹性微振状态。并适时监测地脉动实测点相应测点的脉动谱。下文以测点D5-5 EW方向为例，介绍参数调整的思路与方法。

通过微振荷载激励模型，记录测点D5-5 EW方向的振动波谱（即拟合谱），通过实测解析谱与拟合谱的对比情况（见图4）可知，初始的理论拟合频谱图所得到的主频比实测谱解析频率要小，实测脉动谱揭示边坡在测点D5-5 EW方向微振主频率约为2.0Hz，而模拟微振的测点D5-5 EW方向的主频率为1.0Hz。这说明，边坡初始数值模型的物理力学参数与边坡的实际状态还有一定差距，数值模型的初始参数需要调整。

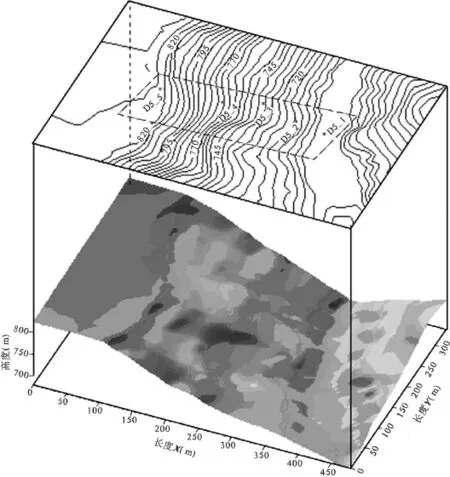
图2　长寿沟黄土边坡DEM模型

图3　长寿沟黄土边坡初始数值模型

经过以上调整方案调整后，测点D5-5拟合频谱和实测解析谱最终达到了一致，如图5所示。调整后的参数见表2。其他各点模拟值与实测值也都取得较好的对应关系。

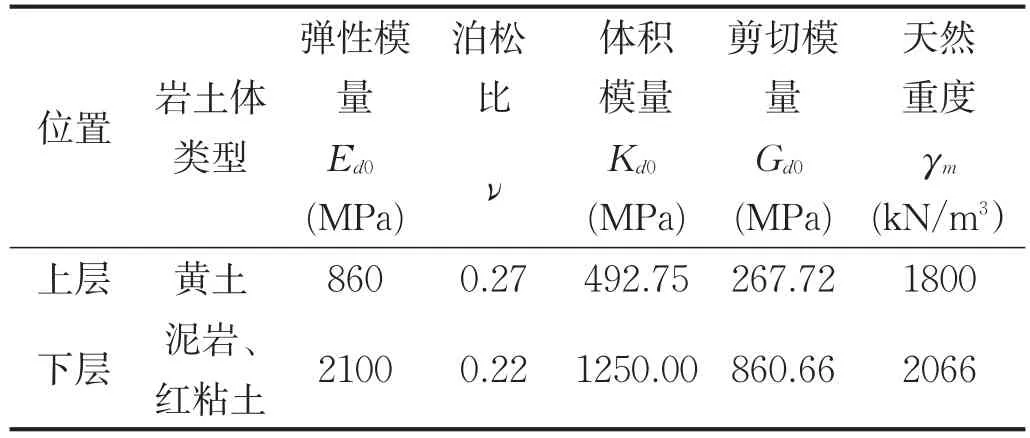
表2　边坡微振数值模拟模型物理力学参数调整值

在模型介质参数调整的过程中，要时刻注意将反演的频谱图与实际观测解析频谱图相比较，同时要兼顾模型的三维速度结构状况，最大化的使实际观测的情况和理论得出的频谱情况一致。如果差距较大，则需要再次对数值模型进行比例粗调或微调模型深度，重新得到反演频谱图，直到反演得到的频谱图与实际观测的结果一致。通过对各个观测点的反复修改，就可以得到地脉动的各个观测点对应的正确层深及介质物理力学参数。

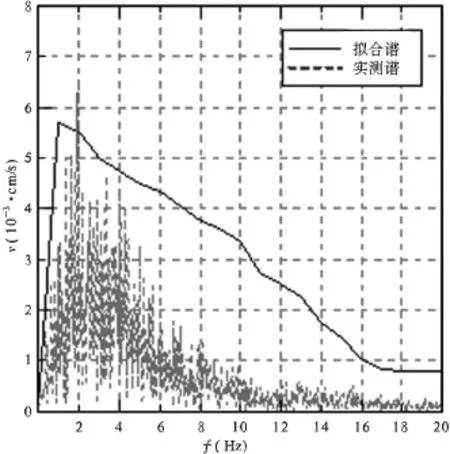
图4　参数调整前实测谱与拟合谱

图5　参数调整后实测谱与拟合

通过对现场测试地脉动的拟合，可以调整获得相对合理的模型与介质物理力学参数，同时为下一步数值模拟的有效性提供了保障。

根据数值模拟结果，计算模拟微振卓越频率与实测脉动卓越频率值基本符合。可见，数值模型及介质力学参数已经调整到了一个合理的取值范围。同时证明，采用该数值模型及介质力学参数可以对该黄土边坡进行有效的数值模拟。地脉动数据就是这样间接地运用于建模之中的。

3　结论

应用地脉动的三维速度结构，进行数值建模的具体步骤如下：

（1）在目标区范围内进行地脉动的观测，获得场地的脉动信息。

（2）对观测的地脉动数据进行解析，得出测点的卓越频率与速度结构谱。

（3）对目标区内的地理资料、地质资料和物探资料进行整理，建立粗略的场地三维速度结构模型。

（4）利用地脉动频谱信息对己建立场地三维速度结构模型进行修补，使之大致与初建模型相符。

（5）采用微振荷载激励模型，拟合实测地脉动解析波谱，根据拟合情况，适时调整模型及介质物理力学参数。

（6）对最后建好的地下三维速度结构模型进行优化，满足数值模拟的需要。

上述工作拓展了地脉动的应用领域，为数值模拟建模提供了新思路，这样建立起来的三维速度结构模型具有良好的地理、地质匹配性，可以运用于各种数值模拟计算。如果地脉动数据足够充分，还可以对大面积区域或城市进行数值建模，进而对大面积区域或城市开展数值模拟计算，然而技巧与方法有待于进一步的深入探索和研究。

［1］兰恒星，伍法权.岩土力学数值模拟中力学参数的确定方法［J］.世界地质，2001（1）：66-71.

［2］王静.应用地脉动的城市地下三维速度结构建模的研究［D］.2008.

［3］郭明珠，谢礼立，高尔根，等.利用地脉动进行场地反应分析研究综述［J］.世界地震工程，1999（3）：14-19.

［4］陶夏新，刘曾武，郭明珠，等.工程场地条件评定中的地脉动研究［J］.地震工程与工程振动，2001（4）：18-23.

Research on Numerical Modeling Using Three-dimensional Velocity Structure of Micro Tremors

CHEN Yun-fei
（Roadway Construction Project Management Center of BeijingMunicipal Roadway Administration Bureau，Beijing 100031，China）

A good three-dimensional model，which is the precondition of numerical simulation，should not only match with real geographical and geological model，but also need certain smoothness. The key of modeling is to determine the depth of each physical or geological layer corresponding with each control point in the target area.In addition，it also needs to make sure the physical and mechanical parameters of media of each layer.The paper uses the analytical spectroscopy of micro tremors as the objective function，by adjusting the model and mechanical parameters of the media，and thus determines the numerical model.This offers a new way for numerical modeling.Finally，combining with the loess slope modeling of Baoji Changshougou，the numerical modeling is attempted with the three-dimensional velocity structure of micro tremors，which expands the applicant space of micro tremors.

micro tremors；numerical model；analytical spectroscopy；fitting

P642

A

1004-5716（2016）05-0001-05

2015-04-30

2015-05-11

陈运飞（1976-），男（汉族），河北邢台人，高级工程师，现从事岩土动力工程学的研究工作。