3-PRRU并联机构自由度分析

柴馨雪，李秦川

(浙江理工大学机械与自动控制学院，杭州 310018)



3-PRRU并联机构自由度分析

柴馨雪，李秦川

(浙江理工大学机械与自动控制学院，杭州 310018)

3-PRRU并联机构具有2个转动和1个移动自由度，是少自由度并联机构中的一个重要分支，具有较大的应用潜力。运用几何代数对3-PRRU并联机构进行自由度分析。首先用几何代数表示了分支和动平台的运动空间；然后通过对分支运动空间求交得到动平台的运动空间，该运动空间的基给出了3-PRRU并联机构自由度的符号表达式。使用几何代数方法所得结果具有几何直观性，且不需要对机构进行约束分析，运算更为简捷。

并联机构；自由度分析；几何代数

0　引　言

两转一移(2R1T)三自由度并联机构是少自由度并联机构中重要的一类，自Hunt[1]于1983年提出3-RPS并联机构以来(R：转动副，P：移动副，S：球铰)，2R1T三自由度并联机构已被用于许多领域，如基于3-PRS并联机构的Z3主轴头[2]、Exechon混联机器人[3]、望远镜姿态控制器[4]、运动模拟器[5]、微操作机器人[6]以及坐标测量机等[7]。各国研究者对该类并联机构开展了大量研究，在运动学分析[8]、尺寸综合[9]、奇异分析[10]、伴随运动[11]等方面取得了重要进展。

自由度指确定机构或运动链位形所需要的独立坐标数[12]。自由度分析是机构应用的前提和基础。少自由度并联机构中多存在冗余约束，其自由度的计算十分困难，各国学者在此方面做了大量工作。黄真等[13]提出了基于约束螺旋理论的自由度分析方法和修正G-K公式，其原理是对各分支施加于动平台的约束系求并，以得到动平台被约束的自由度。该方法适用于全部9类少自由度并联机构。Herve[14]采用基于群论方法的并联机构位移子群求交方法来分析自由度。Staffetti[15]提出一种基于Grassmann-Cayley代数的分支运动空间的交集计算方法。

几何代数又被称为Clifford代数，是一种几何应用方面极具潜力的计算方法，由Clifford[16]在1876年首次提出，故又被称作Clifford代数。Hestenes[17]将Clifford代数进行几何意义上的解释，从而称它为几何代数。在处理几何应用问题时，几何代数在几何解释方面具有其他方法无法比拟的优势，已被广泛应用到物理[18-19]、神经计算[20]、信号及图像处理[21]、机器视觉[22]、计算机图形学[23]和机器人学[24-25]等领域。Hildenbrand和Zamora等[26-27]用共形几何代数方法对机器人的运动学逆解等问题进行了分析。Aristidou和Lasenby[28-29]用几何代数方法求解运动学逆解，并且提出了一种有效的运动学逆解迭代求解器Fabrik。Lasenby等[30]提出了一种基于几何代数的机器视觉结构与运动评估方法。Tanev[31]用几何代数方法对四自由度并联机构进行了奇异分析。

本文运用几何代数对3-PRRU并联机构自由度进行分析。首先用利用几何代数中的外积表达了分支和动平台的运动空间，然后通过对分支运动空间求交得到动平台的运动空间，该运动空间的基给出了3-PRRU并联机构自由度的符号表达式。

1　几何代数基础

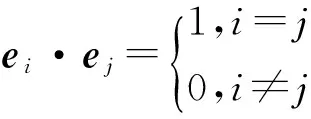
(1)

已知向量a和b，则a和b的几何积可以定义为：

ab=a·b+a∧b

(2)

其中：a·b是向量a和b的内积，a∧b是向量a和b的外积。

2个向量a和b的外积表示一个有方向的平面度量，具体表示为向量b沿着向量a扫过而形成的平行四边形，如图1(a)所示。外积具有反对称性，即a∧b=-b∧a。

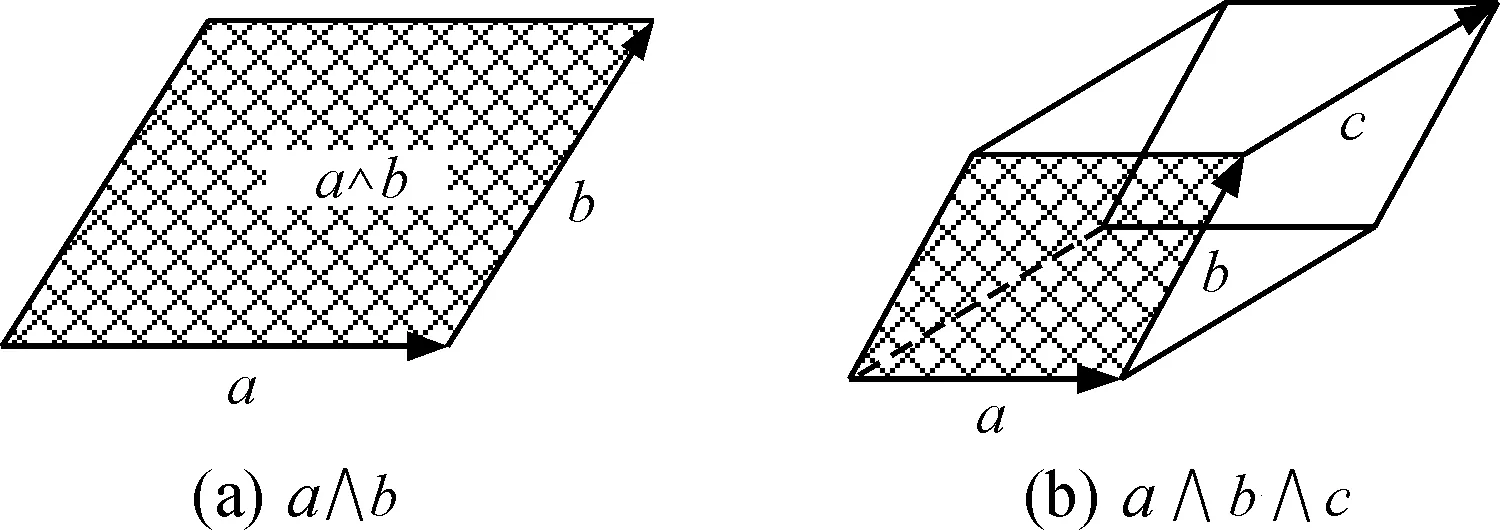
图1　几何积的几何表达

3个向量a、b和c的外积表示一个有方向的空间度量，具体表示为面度量a∧b沿着向量c扫过而形成的空间，如图1(b)所示。外积运算满足结合律，即(a∧b)∧c=a∧(b∧c)。

k个向量a1,a2,…,ak的外积组成一个k维的片积(blade)：

〈A〉k=a1∧a2∧…∧ak

(3)

其中k是片积的阶(grade)。k阶片积的几何意义为一个由k个向量张成的子空间。

In=e1e2e3…en

(4)

k阶片积A的对偶空间为这个k维子空间的正交补空间：

(5)

几何代数可以表示螺旋理论，螺旋理论与几何代数的关系在文献[32]中有详细阐述。本文将螺旋理论与几何代数运算之间关系用表格形式列出，如表1所示。

表1　螺旋理论与几何代数的关系

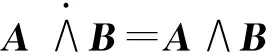
(6)

(7)

交集可以看作是向量空间交集的代数表达形式。

A和B的交集还满足德摩根定律，即：

(8)

2　自由度分析方法

串联运动链的运动空间可以表示为组成该串联运动链的每个关节的运动子空间的并集。因此第i个分支上的运动空间可以表示为分支上mi个关节运动子空间的并集：

Ai=Si1∧…∧Sij∧…∧Simi

(9)

其中Sij表示并联机构第i个分支上第j个运动螺旋。

mi阶的片积Ai表示第i个分支上所有mi个关节张成的运动空间。如果式(9)中的向量Sij和Sij+1线性相关，需要在移除线性相关项后再进行计算。

相反地，并联机构动平台的运动空间是所有分支运动链的运动空间的交集。根据式(7)可得到分支运动子空间Ai和Ai+1的交集为：

(10)

如果机构的分支数目为n，则动平台的运动空间M为所有n个分支运动子空间的交集，即：

M=A1∨…∨Ai∨…∨An

(11)

其中动平台的运动空间M的阶数即为机构自由度的数目。

3　3-PRRU并联机构自由度分析

图2为一个3-PRRU并联机构，其中U表示虎克铰。分支一及分支二的R副轴线相互平行，且与分支一及分支二上的P副轴线垂直。分支三上的R副轴线与前两个分支上的R副轴线相互垂直，且与分支三上的P副轴线垂直。R副经过点Ai(i=1,2,3)和Bi。3个U副的中心分别经过点Ci(i=1,2,3)，且这3点都在动平台上为共线关系，如图2所示。该机构中3个P副为驱动副。

图2　3-PRRU并联机构

定平台是一个等腰三角形△DEF，其形心为点o，且满足DF=FG。固定坐标系oxyz如图2所示建立，其中x轴沿着OG，y轴沿着OF，z轴朝上。一般位形下的结构参数如图3所示。

假设3-PRRU并联机构在一般位形下且未达到奇异位形。建立从动坐标系o′x′y′z′相对于固定坐标系oxyz的Y-X-Z欧拉角姿态变换，即：首先绕初始位形的y轴转θ角度，其次绕着当前的x轴转过ψ角度，最后绕着当前z轴转ψ角度。旋转变换矩阵如下：

图3　3-PRRU并联机构结构参数

(12)

机构中点A1、A2、A3、B1、B2、B3、C1、C2、C3的坐标及U副的转动轴线相对于固定坐标系的方向矢量如表2所示。

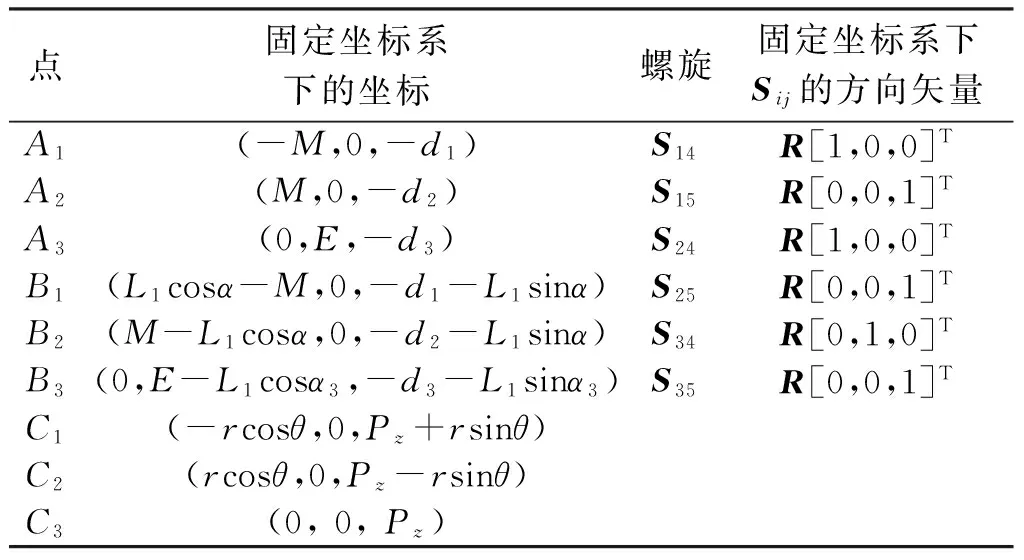
表2　3-PRRU并联机构的结构参数

sinψ(Pz+rsinθ)e4+cosψ(r+Pzsinθ)e5+

rcosθsinψe6

(13)

分支一上运动空间为组成该串联分支的所有关节运动子空间的并集：

=S11∧S12∧S13∧S14∧S15

=a(e1∧e2∧e3∧e4∧e6-rcosθe1∧e2∧e4∧e5∧e6+(rsinθ-PZ)e2∧e3∧e4∧e5∧e6)

(14)

其中a是一个非零标量系数，对自由度分析没有影响，可以忽略。

同理，分支二上的每个关节螺旋在Γ6中的表达式为：

sinψ(Pz-rsinθ)e4-cosψ(r-Pzsinθ)e5-

rcosθsinψe6

(15)

分支二上运动空间为组成该串联分支的所有关节运动子空间的并集：

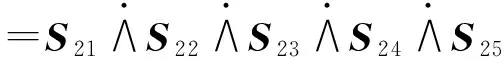
=S21∧S22∧S23∧S24∧S25

=b(e1∧e2∧e3∧e4∧e6+rcosθe1∧e2∧e4∧e5∧e6+(rsinθ-PZ)e2∧e3∧e4∧e5∧e6)

(16)

其中b是一个非零标量系数，对自由度分析没有影响，可以忽略。

分支三上的每个关节螺旋在Γ6中的表达式为：

Psinψe4+Pzsinθcosψe5

(17)

分支三上运动空间为组成该串联分支的所有关节运动子空间的并集：

=S31∧S32∧S33∧S34∧S35

=c(e1∧e2∧e3∧e5∧e6+Pze1∧e3∧e4∧e5∧e6)

(18)

其中c是一个非零标量系数，对自由度分析没有影响，可以忽略。

根据式(10)可以得到分支一和分支二的运动子空间的交集：

A12=A1∨A2

=d(PZcosθe2∧e4∧e5∧e6+sinθe2∧e3∧e4∧e6+cosθe1∧e2∧e4∧e6)

(19)

其中d是一个非零标量系数，对自由度分析没有影响，可以忽略。

根据式(11)，可以得到分支一、分支二和分支三的运动子空间的交集，即：

M=A1∨A2∨A3

=A12∨A3

=M1∧M2∧M3=f(cosθe1-sinθe3+Pzcosθe5)∧(e2-Pze4)∧e6

(20)

其中f是一个非零标量系数，对自由度分析没有影响，可以忽略不计。

式(20)表示分支一、分支二和分支三的运动子空间的交集是一个阶数为3的片积。这个3阶片积表示3-PRRU并联机构动平台上的运动空间，表明该机构具有3个自由度，分别为M1=cosθe1-sinθe3+Pzcosθe5,M2=e2-Pze4,M3=e6。M1是一条与C1C3重合的直线，表示一个绕线C1C3的转动自由度。M2是一条经过点C3且与y轴平行的直线，表示一个绕这条线的转动自由度。M3表示沿z轴移动的移动自由度。

4　结　论

本文运用几何代数对3-PRRU并联机构进行自由度分析，通过对3条PRRU支链的运动空间求交得到动平台运动空间的解析表达式。从该解析表达式中可以看出，该机构有3个自由度，分别为绕C1C3的转动、绕过点C3且与y轴平行的直线的转动以及沿z轴移动。使用几何代数可直接对3-PRRU并联机构分支运动空间进行求交计算，这种方式更符合人对并联机构自由度的思维习惯，并且避免了约束方程的求解，使得计算过程更加简单。

[1]HUNTKH.Structuralkinematicsofin-parallel-actuatedrobotarms[J].JournalofMechanisms,Transmissions,andAutomationInDesign,TransactionsoftheASME,1983, 105(4)：705-712.

[2]WAHlJ.Articulatedtoolhead：US6431802B1 [P]. 2000-11-05.

[3]BIZM,JINY.KinematicmodelingofExechonparallelkinematicmachineoriginalresearcharticle[J].RoboticsandComputer-IntergratedMunufacturing, 2011, 27 (1)：186-193.

[4]CARRETEROJA,NAHONM,GOSSELINCM,etal.Kinematicanalysisofathree-dofparallelmechanismfortelescopeapplications[C]//ASMEDesignAutomationConference,September15-20, 1997,Sacramento,CA,California：1-8.

[5]POULIOTNA,NAHONMA,GOSSELINCM.Motionsimulationcapabilitiesofthree-degrees-of-freedomflightsimulators[J].JournalofAircraft, 1998, 35(1)：9-17.

[6]YUJJ,HUYD,BISS,etal.Kinematicsfeatureanalysisofa3DOFin-parallelcompliantmechanismformicromanipulation[J].ChineseJournalofMechanicalEngineering, 2004, 17(1)：127-131.

[7]LIUD,CHER,LIZ,LUOX.Researchonthetheoryandthevirtualprototypeof3-DOFparallel-linkcoordinating-measuringmachine[J].IEEETransInstrumMeas, 2003, 52(1)：119-25.

[8]LEEK,SHAHDK.Kinematicanalysisofathreedegreesoffreedomin-parallelactuatedmanipulator[J].IEEEJournalofRoboticsandAutomation, 1988, 4(3)： 354-360.

[9]TSAILW,KIMHS.Kinematicsynthesisofaspatial3-RPSparallelmanipulator[J].JournalofMechanicalDesign, 2003, 125(1)：92-97.

[10]JOSHISA,TSAILW.Jacobiananalysisoflimited-DOFparallelmanipulator[J].JournalofMechanicalDesign, 2002, 124(2)：254-258.

[11]CARRETEROJA,PODHORODESKIRP,NAHONMA,etal.Kinematicanalysisandoptimizationofanewthreedegree-offreedomspatialparallelmanipulator[J].JournalofMechanicalDesign, 2000, 122(1)：17-24.

[12]IONESCUTG.Terminologyformechanismsandmachinescience[J].MechanismandMachinetheory, 2003, 38(7-10): 819-825.

[13] 黄真, 刘婧芳, 曾达幸. 基于约束螺旋理论的机构自由度分析的普遍方法[J]. 中国科学 技术科学, 2009, 39(1): 84-93.

[14]HERVEJM.TheLiegroupofrigidbodydisplacements,afundamentaltoolformechanismdesign[J].MechanismandMachineTheory, 1999, 34(5): 719-730.

[15]STAFFETTIE.KinestaticanalysisofrobotmanipulatorsusingtheGrassmann-Cayleyalgebra[J].RoboticsandAutomation,IEEETransactionson, 2004, 20(2): 200-210.

[16]CLIFFORDWK.ElementsofDynamic:anIntroductiontotheStudyofMotionandRestinSolidandFluidBodies[M].London：MacMillanandCompany, 1878.

[17]HESTENESD.NewFoundationsforClassicalMechanics[M]. 2nded.Dordrecht:Springer, 1999.

[18]BAYLISWE.Clifford(Geometric)Algebras:withApplicationsinPhysics,Mathematics,andEngineering[M].Boston:BirkhluserBoston, 1996.

[19]DESABBATAV,DATTABK.GeometricAlgebraandApplicationstoPhysics[M].Florida:CRCPress, 2006.

[20]BUCHHOLZS.ATheoryofNeuralComputationwithCliffordAlgebras[D].Kiel:UniversityofKiel, 2005.

[21]TIRKKONENO,HOTTINENA.Square-matrixembeddablespace-timeblockcodesforcomplexsignalconstellations[J].InformationTheory,IEEETransactionson, 2002, 48(2): 384-395.

[22]SOMMERG.Applicationsofgeometricalgebrainrobotvision[C]//LIH,OLVERPJ,SOMMERG.ComputerAlgebraandGeometricAlgebrawithApplications.Berlin:Springer-Verlag, 2005: 258-277.

[23]SOMMERG.GeometricComputingwithCliffordAlgebras:TheoreticalFoundationsandApplicationsinComputerVisionandRobotics[M].Berlin:Springer-VerlagBerlinHeidelberg, 2001.

[24]HILDENBRANDD-ID.GeometricComputinginComputerGraphicsandRoboticsUsingConformalGeometricAlgebra[D].Tübingen:UniversitätTübingen, 2006.

[25]DORSTL,LASENBYJ.GuidetoGeometricAlgebrainPractice[M].London:Springer-VerlagLondon, 2011.

[26]HILDENBRANDD,ZAMORAJ,BAYRO-CORROCHANOE.Inversekinematicscomputationincomputergraphicsandroboticsusingconformalgeometricalgebra[J].AdvancesinAppliedCliffordAlgebras, 2008, 18(3-4): 699-713.

[27]ZAMORAJ,BAYRO-CORROCHANOE.Inversekinematics,fixationandgraspingusingconformalgeometricalgebra[C]//Proceedingof2004IEEE/RSJInternationalConferenceonIntelligentRobotsandSystems.Sendai, 2004: 3841-3846.

[28]ARISTIDOUA,LASENBYJ.Inversekinematicssolutionsusingconformalgeometricalgebra[M]//DORSTL,LASENBYJ.GuidetoGeometricAlgebrainPractice.London:Springer-VerlagLondon, 2011: 47-62.

[29]ARISTIDOUA,LASENBYJ.FABRIK:afast,iterativesolverfortheinversekinematicsproblem[J].GraphicalModels, 2011, 73(5): 243-260.

[30]LASENBYJ,FITZGERALDWJ,LASENBYAN,etal.Newgeometricmethodsforcomputervision:anapplicationtostructureandmotionestimation[J].InternationalJournalofComputerVision, 1998, 26(3): 191-213.

[31]TANEVTK.Singularityanalysisofa4-DOFparallelmanipulatorusinggeometricalgebra[M]//LENARCICJ,ROTHB.AdvancesinRobotKinematics:Springer, 2006: 275-284.

[32]LiQ,ChaiX.Mobilityanalysisoflimited-DOFparallelmechanismsintheframeworkofgeometricalgebra[J/OL].JournalofMechanismsandRobotics, 2015. (2015-11-23)[ 2015-12-31].http://mechanismsrobotics.asmedigitalcollection.asme.org/article.aspx?articleid=2475687.DOI:10.1115/1.4032210.

(责任编辑： 康锋)

Mobility Analysis of a 3-PRRU Parallel Mechanism

CHAIXinxue，LIQinchuan

(Faculty of Mechanical Engineering and Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

The 3-DOF parallel mechanism (PM) with one translational and two rotational (1T2R) DOFs is an important category of the lower-mobility PM. Mobility is a basic property of a mechanism. This paper analyzes the mobility of a 3-PRRU PM based on geometric algebra (GA). Firstly, the twist space of the limb and moving platform are represented by geometric algebra. Then, the twist space of the moving platform is obtained by taking the intersection of the twist space of all the limbs. Finally, the symbolic expression of mobility of a 3-PRRU PM is given by the basis of the twist space on the moving platform. Using GA-based method, geometric intuition is the advantage of this method. Without resorting constraint equation, the calculation is more convenient and fast.

parallel mechanism；mobility anlaysis；geometric algebra

10.3969/j.issn.1673-3851.2016.03.007

2015-12-31

国家自然科学基金项目(51525504)

柴馨雪(1988-)，女，内蒙古赤峰人，博士研究生，主要从事并联机器人方面的研究。

李秦川，E-mail：lqchuan@zstu.edu.cn

TP24

A

1673- 3851 (2016) 02- 0192- 06 引用页码： 030401