基于Pro/E的船舶运动试验台运动仿真与控制分析

党　琪，叶建华，胡中望，蔡佳俊

(上海振华重工(集团)股份有限公司a.陆上重工设计研究院；b.科技管理部，上海，200125)



基于Pro/E的船舶运动试验台运动仿真与控制分析

党琪，叶建华，胡中望，蔡佳俊

(上海振华重工(集团)股份有限公司a.陆上重工设计研究院；b.科技管理部，上海，200125)

为检验船载设备在海浪扰动下工作性能，研制模拟船舶运动的试验平台，应用Pro/ENGINEER建立试验平台模型，采用骨架模型完成其三维实体装配，再进行运动仿真。通过MATLAB对控制系统进行仿真分析。与用实船测试相比，认为该平台具有可控性，无破坏性、经济性等优点。

船舶运动；试验平台；运动仿真

Stewart机构具备精度高、承载力强等优点，目前其广泛应用于运动模拟、空间飞行器对接、舰艇观测台等系统。

本文应用Pro/E软件建立试验平台的模型，由动平台、定平台和6根阀控液压缸通过铰链将他们连接起来组成船舶运动试验平台。该平台经控制器实时控制，能提供6自由度的瞬时过载，完成船舶的艏摇、横摇、纵摇、垂荡等运动的模拟[1]。曾有一种4自由度的试验台，由水平移动台、垂直升降台、旋转台和摆动台组成，其可在实验室条件下模拟出在不同海况下船舶及其上通讯系统的运动[2]，其升降距离和摆动角度均很有限。而本文中的船舶运动试验台的工作空间较大，并针对特定海况，对该试验平台进行合理的轨迹规划，使其能反映船舶实际的运动姿态，为波浪补偿控制器的性能检测提供试验环境，还可检查船载设备在海浪影响下的工作情况。

1　试验台的位置分析及结构

船舶运动试验平台机构原理见图1。有学者提出一种较简单的位置正解方法[3]，为方便起见,分别在下平台和上平台上建立坐标系，坐标系坐标系S0固连于下平台，坐标系SN固连于上平台，从坐标系SN到S0的变换矩阵0TN为

图1　试验平台的机构简图

(1)

式中：P=[x,y,z]T为ON坐标系S0中的位置向量；矩阵R是一个3×3的方向余旋矩阵，其每一列为坐标系SN的XN、YN、ZN轴在坐标系S0中的方向余弦。

经过简化，得到包含21个方程的方程组，可以写成下列形式：

AX=0

(2)

式中：A——21×21的矩阵，其元素为my的多项式；

X——21×1的列向量。

对其求解较复杂，采用计算机辅助推导软件求解。

在运动平台的结构设计中工作空间分析是主要考虑因素之一。工作空间的大小决定了平台的活动空间。由于并联机构位置和姿态具有复杂的耦合性，工作空间是一个六维空间。

影响并联机器人工作空间的因素主要有杆长的限制,运动副转角的限制及连杆的干涉[4]。

平台的运动过程中会遇到特殊的位置，在这些位置机构或者处于死点不能运动、或者失去稳定，甚至自由度也发生改变、还会出现受力状态变坏，损坏机构的情况。这种位形称为机构的奇异位形[5]。平台的支链应适当布置以提高其性能，如通过合理布局提高其工作空间同时减少奇异位形，结构设计中支链的布置要避免结构奇异[6]。

伺服缸为并联平台提供驱动力输入，设计伺服缸必须满足在整个运动过程中能够驱动负载按期望的速度运动，能满足最大负载以内，液压缸活塞杆的强度满足要求。根据试验平台对伺服缸缸行程和载荷要求，确定液压缸的负载力及行程。阀控非对称液压缸，其往返特性不—致。实验证明，非对称液压缸考虑负载重力影响的情况下，应取面积比ε=0.67，根据液压伺服系统的负载匹配条件以及活塞杆的强度，确定液压缸的结构尺寸。上平台铰点分布圆半径920 mm，下平台铰点分布圆半径950 mm，上平台短边夹角15°，下平台短边夹角15°，各支链的初始长度1 400 mm，中位高度1 220 mm。

2　试验平台的虚拟装配及运动仿真

2.1试验平台的虚拟装配

在试验平台的装配中首先要建立骨架模型[7]。骨架模型在自顶而下的设计中具有极其重要的地位，包含了用以控制全部零件的设计需求，是设备组装的基础。在Pro/ENGINEER中提供的骨架模型，对于复杂装配是一个非常有用的功能。他允许使用者在加入零组件之前，先设计好每个零件在空间中的静态位置，可以利用此骨架模型将每个零件装配上去。

选择“骨架模型”单选按钮，保持系统自动给骨架模型命的名称，单击“确定”按钮，在“创建方法”选项组中保持“复制现有”单选按钮，单击该对话框的“浏览”按钮，骨架模型被自动装配进组件。在模型树上右击该骨架模型，在弹出的菜单中选择“打开”命令，在新窗口中打开该文件。在当前窗口中完成并联平台的骨架的设计，结构尺寸与实际完全一致。然后单击“将元件添加到组件”按钮，选择首先要装配的零件，零件出现在图形窗口中。在弹出的“元件放置”对话框内，合理设置约束和连接的类型，使零件准确地装配在骨架上，同理完成其余零件的装配。

2.2试验平台的运动仿真

先完成试验平台的各零部件的实体设计，再进行平台的虚拟装配，最后应用Mechanism模块进行平台的运动仿真。能够生动形象地进行该平台的运动模拟，并制作出清晰的动画，从而了解其运动能力，平台的极限位置，揭示机构的合理运动方案及有效的控制算法，从而解决在试验平台设计及运动过程中的问题，避免了直接操作实物，可能会造成的机械故障和对设备的损坏。

根据6自由度并联机器人的支链选取的系统方法[8]，得到数种可行支链形式供后续优化设计。由于6-SPS型机构含有6个局部自由度，所以其与6-UPS型机构的运动等效。下面就采用等效机构来进行运动分析，这样可以简化运动副的定义步骤。建立好的运动模型如图2所示。

图2　运动仿真过程

举例说明某海况下的船舶偏航运动的仿真过程。在主菜单中选择“应用程序”中的“Mechanism命令”即可进入该模块环境。

建立伺服电动机能够为机构提供“动力”，通过设置伺服电动机可以实现旋转及平移运动，并且能以函数的方式定义运动轮廓。在“轮廓”选项卡中，可以指定伺服电动机的位置、速度及加速度随时间变化而变化的规律。设置界面如图3所示。目前供了9种定义方式，这里先给第一个伺服电动机选择余弦方式，其方程式为

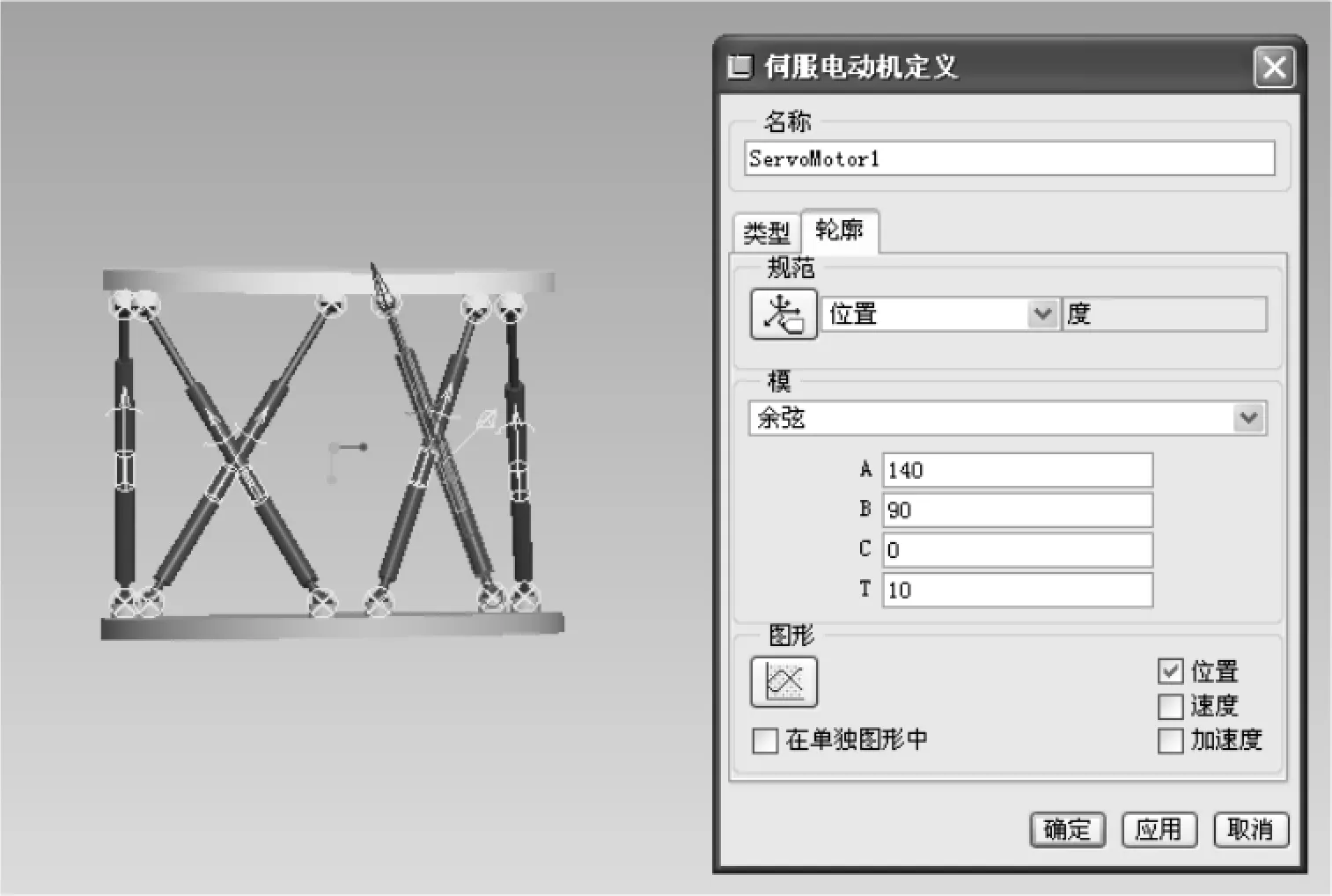
图3　设置伺服电动机

y=Acos(360×t/T+B)+C

(3)

根据轨迹要求合理设置振幅A、相位B、偏距C以及周期T。待模拟的航行海域的海况参数为波浪幅值A=1.2 m，周期T=8 s，波浪速度v=0.94 m/s，波浪加速度a=0.74 m/s2。

采用相同步骤，分别设置其余的伺服电动机，以满足其各种运动的要求。这里6个电动机均采用“余弦”方式，为使平台能按特定轨迹而运动，即准确的模拟特定海况，那么各个电动机的A、B、C、T这4个数值的设置就要参考由位置反解公式计算出的各缸位移。然后进行运动分析，察看分析结果。回放分析结果可以播放建立的分析并输出成为动画文件。播放动画的同时可以进行干涉检查、动画进度表的设置，单击“捕获”按钮，进行必要的设置后即可进行动画的录制。

先在上平台中心加上载荷，单击“生成分析的测量结果”按钮，在“图形类型”选项里选择“测量与时间”，单击“创建新测量”按钮，弹出如图4所示的窗口。分别定义出要分析的各个点和连接轴，在“类型”选项里选择“位置”，在“评估方法”选项里选择“每个时间步长”。

图4　创建新测量

选择好“测量”和“结果集”后，单击“绘制所选测量的图形”按钮，弹出如图5所示的测量图形。从图5可以看出0～20 s内各轴运动较平稳，20 s后各轴开始产生剧烈的振动。

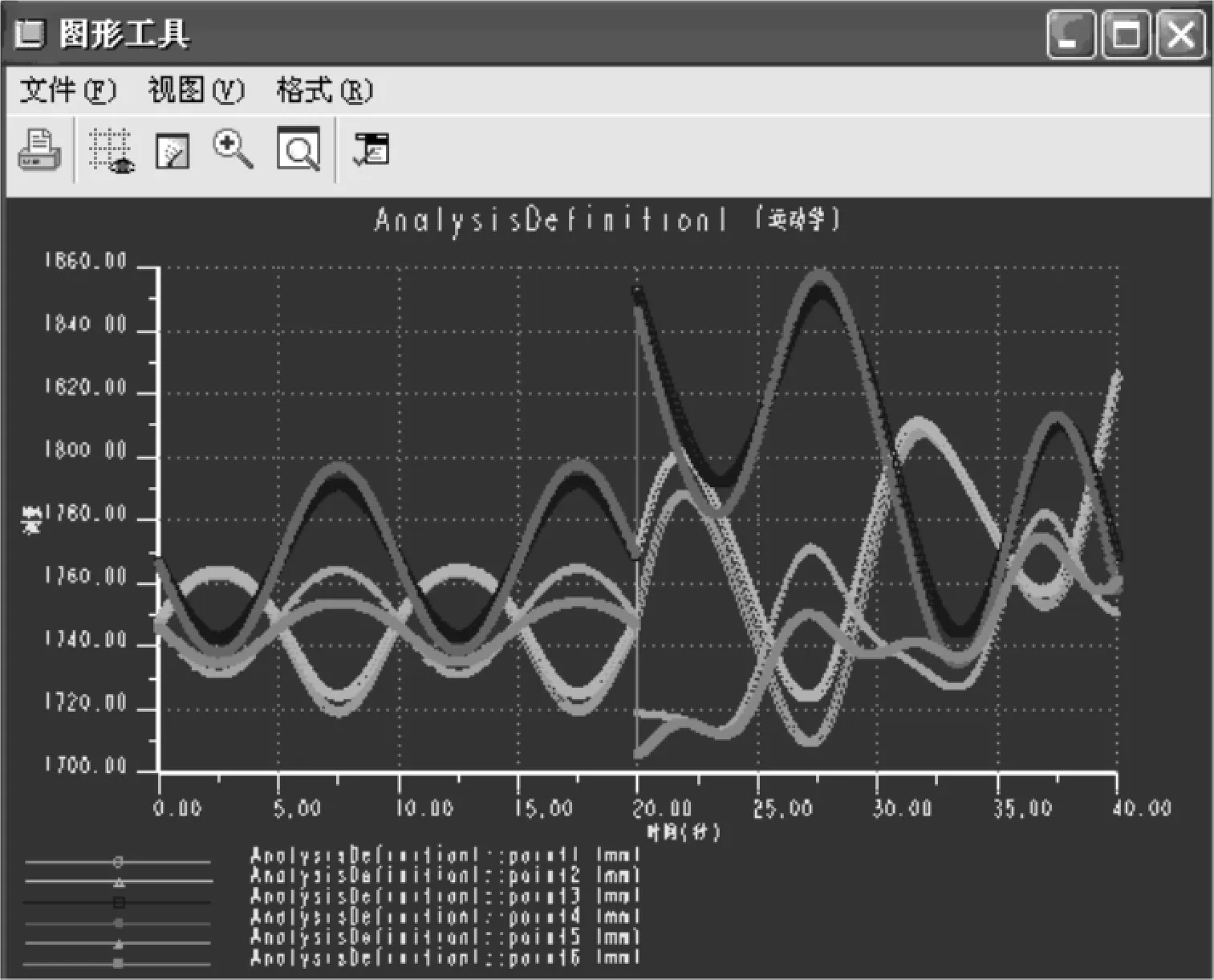
图5　各液压缸顶点随时间的位置曲线

3　控制系统分析及应用

3.1控制系统分析

液压系统液体体积可压缩、泄漏系数等因素的改变，使得液压系统往往是非线性的。要对其线性化，用线性化传递函数在操作点附近近似表达系统的特性[9]。由于试验平台各液压缸的控制是互相独立的，并且各轴线的结构和控制系统是相同的，故此处仅对单轴线的液压伺服系统的数学模型进行分析，建立其控制系统的模型，过程如下。

1)液压缸的传递函数。可通过从伺服阀输出流量QL和液压缸位移XP求得。

(4)

式中：ζh——阻尼比，

ωh——液压缸固有频率。

计算参数：有效体积弹性模量700 MPa，活塞面积0.005 027 m2，流量压力系数0.83×10-12，活塞及负载的粘性阻尼系数6×105，液压缸的固有频率358.47，阻尼比0.2。

2)阀的传递函数。

(5)

式中：ωsv——自然频率；

ζsv——阻尼比；

Ksv——阀的流量增益。

经过计算，传函参数分别为：ωsv=815.2，ζsv=0.6，Ksv=9.373 2×10-5。

在MATLAB软件中对该系统进行仿真，输入信号幅值为1、信号输入时间为0.5 s的阶跃信号。通过ZN整定方法，先使系统只受纯比例作用，将积分时间调到最大，微分时间调到最小。再将比例增益由较小的值逐渐增大，直到系统出现等幅振荡的临界稳定状态，随后再由频率响应整定公式计算出比例增益、积分增益和微分增益。经过调试得到响应速度快、超调量较小的系统阶跃响应，见图6。

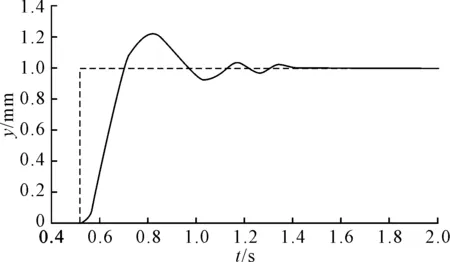
图6　PID控制的阶跃响应

3.2试验平台的应用

该试验台可用于检验波浪补偿绞车控制系统的性能，其步骤为：首先，在试验平台上安装好被试绞车和MRU(运动参考单元)。其次，给船舶运动试验平台控制器设定好运动参数后，试验平台就能模拟出绞车在海上起吊作业的工况，MRU检测并反馈试验台的运动参数给AHC(主动波浪补偿)控制器。最后，经过程序计算并对绞车马达发出控制指令，使绞车能根据运动平台的运动而调整旋向，即运动平台向上运动时，绞车快速放绳；运动平台向下运动时，绞车快速收绳。

4　结论

该船舶运动试验平台与其他试验平台相比，具有6个自由度、结构尺寸合理、响应速度快，满足模拟船舶运动的要求。在测试带波浪补偿功能的绞车时，与租用工程船装载被试绞车，到特定海域做实船试验相比，船舶模拟平台不受天气和风浪的影响，具有较高的经济性，并且安全可靠。此外，该试验平台还可用于检验船载设备的性能及航海驾驶训练。

[1] 尹茜,陈红卫.随机海浪下船舶摇荡的计算机仿真[J].微电子学与计算机,2007,24(6):191-192.

[2] 汪亭玉,梁忠诚.船舶大气激光通信用模拟平台研究与实验[J].船海工程,2008,37(6):96-99.

[3] ZHANG C D, SONG S M. Forward position analysis of nearly general stewart platforms[J]. Spatial Mechanisms and Mechanical Systems,1992,45(12):81-84.

[4] 黄真.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.

[5] 黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.

[6] MA O. Architecture singularities of platform manipulators[A]. Proceedings of the IEEE International Conference on Robotics and Automation[C]∥Sacramento, 1991,30(5)：1542-1547.

[7] 韩玉龙.Pro/ENGINEER Wildfire 组件设计与运动仿真[M].北京:清华大学出版社,2004:264-327.

[8] 陈峰,费燕琼,赵锡芳.六自由度并联机器人的支链选取[J].机器人,2005,27(5):65-72.

[9] 刘俊,覃刚,王强，等.基于AMESim-Simulink的电液伺服系统的控制器设计[J]. 船海工程,2015,44(1):122-125.

Motion simulation of ship's motion platform based on Pro/E and control analysis

DANG Qi, YE Jian-hua, HU Zhongwang, CAI Jia-jun

(a. Land Heavy Industry Design & Research Institute,b. Dept. of Technology Management, Shanghai ZhenHua Heavy Industries Co. Ltd., Shanghai 200125, China)

In order to test the performance of the shipboard equipment in offshore, the test platform is developed for simulating ship motions. The model of test platform is established by Pro/ENGINEER, and the platform is assembled through the skeleton model function, then the motion simulation is carried out. The control system of the platform is analyzed by MATLAB simulation. Compared with test the equipment by using real ship, the proposed test platform has advantages of controllability, no damage and economy.

ship's motion; test platform; motion simulation

10.3963/j.issn.1671-7953.2016.01.004

2015-09-21

2015-10-14

党琪(1980-)，男，硕士，工程师。

U666.16

A

1671-7953(2016)01-0019-04

研究方向:波浪补偿及机电系统智能控制

E-mail:dangqi6@163.com