基于MDD的多状态网络二端可靠性算法
郭晓勇,董荣胜,朱阳阳
(桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004)
基于MDD的多状态网络二端可靠性算法
郭晓勇,董荣胜,朱阳阳
(桂林电子科技大学 计算机与信息安全学院,广西 桂林541004)
为解决多状态网络二端可靠性问题,提出了多值离散概率模型MDD_WS2TR,基于该模型给出了MFMC_MDD算法。该算法基于最大流最小割思想,对最小割中的边进行合并,过滤掉稠密网络中无关紧要的边,降低了计算量。在构建网络MDD的过程中,定义了操作算子TBoolean,该算子对MDD进行剪枝,压缩了最大流的状态组合空间,降低了MDD之间进行合并操作的复杂度。在一组随机流网络图上对MFMC_MDD算法进行测试,验证了MFMC_MDD算法的有效性。
多状态;最大流;最小割;MDD;可靠性
在传统的二状态网络中,系统的组件只有工作和失效2种状态,系统的可靠性往往指的是源点s和终点t的连通概率。当组件的状态为容量时,也只有0和另外一个正整数作为2种状态。但是,在多状态网络中,每个节点或边都有若干可能的容量,近几年来,许多研究者对多状态网络模型做了大量的研究。给定需求水平d,此类具有离散、随机容量的多状态二端网络的可靠性被定义为:从源点s到终点t,最大流大于等于需求水平d的概率[1]。针对该问题,现有的研究方法主要基于完全枚举法和分解法。其中,完全枚举法需要枚举所有边的状态组合,计算复杂度很高。Doulliez等[2]提出一种著名的分解算法,将状态空间不断地分解,直至找到所有能够满足要求的状态集合。而Alexopoulos[3]指出这个方法存在错误,可能得到一个不正确的答案。针对复杂系统,Ramirez-Marquez 等[4]提出了一个蒙特卡洛仿真的近似方法来计算多状态网络二端可靠性,但该方法的错误率达20%。还有一些学者[5-10]基于最小路集(minimal paths,简称MPs)或最小割集(minimal cuts,简称MCs)提出一种间接的方法寻找多状态向量集(d-MPs/d-MCs),再通过容斥原理计算多状态网络二端可靠性。然而,寻找MPs/MCs、d-MPs/d-MCs以及容斥原理都是NP-hard问题。2008年Jane等[11]首次提出基于d-flows的分解方法,无需预先求出d-MPs/d-MCs。2010年Jane等[1]提出一种基于d-cuts的分解算法,但该算法中的d-flows/d-cuts本质上类似于一个d-MPs/d-MCs,并且需要预先用最大流算法求得所有能够传输d个需求的状态向量,以这些状态向量作为临界向量,低于这个临界向量的集合被继续分解,直到筛选出所有满足要求的状态向量,复杂度依然很高。
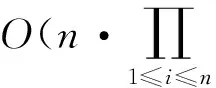
因此,结合多值决策图(multi-valued decision diagram,简称MDD)技术,提出一种可以更大程度地降低计算复杂度的MFMC_MDD算法。该算法利用MDD固有的特性,实现对状态组合空间的隐式表示与搜索,提高了算法的执行效率。相比于现存的d-MPs/d-MCs的研究方法,避免了求多状态向量集d-MPs/d-MCs,也避免了用容斥原理计算可靠度。为了构建网络的MDD,基于最大流最小割思想定义了OrSum、AndMin、TBoolean三个操作算子。其中,TBoolean操作算子对MDD进行剪枝,压缩状态空间,有效缓解了状态空间爆炸。求解网络可靠度时,采用递归的方法遍历网络的MDD,遍历时间为O(n),其中n表示生成的MDD的节点个数。为了检验MFMC_MDD算法的可行性,在一组随机流网络图上对算法进行测试,验证了算法的有效性。这种新的研究方法为多状态网络二端可靠性求解提供了新的思路。
1 多状态网络二端可靠性的多值离散概率模型
1.1多状态网络
定义1多状态二端网络的形式化模型为

其中:N为节点集合;s为源点;t为终点;E={ei|1≤i≤n}为边的集合;M={M1,M2,···,Mn},Mi为边ei的最大容量。
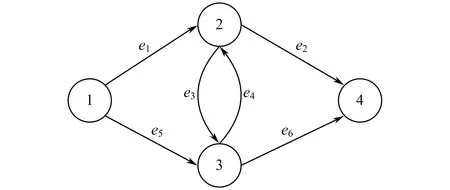
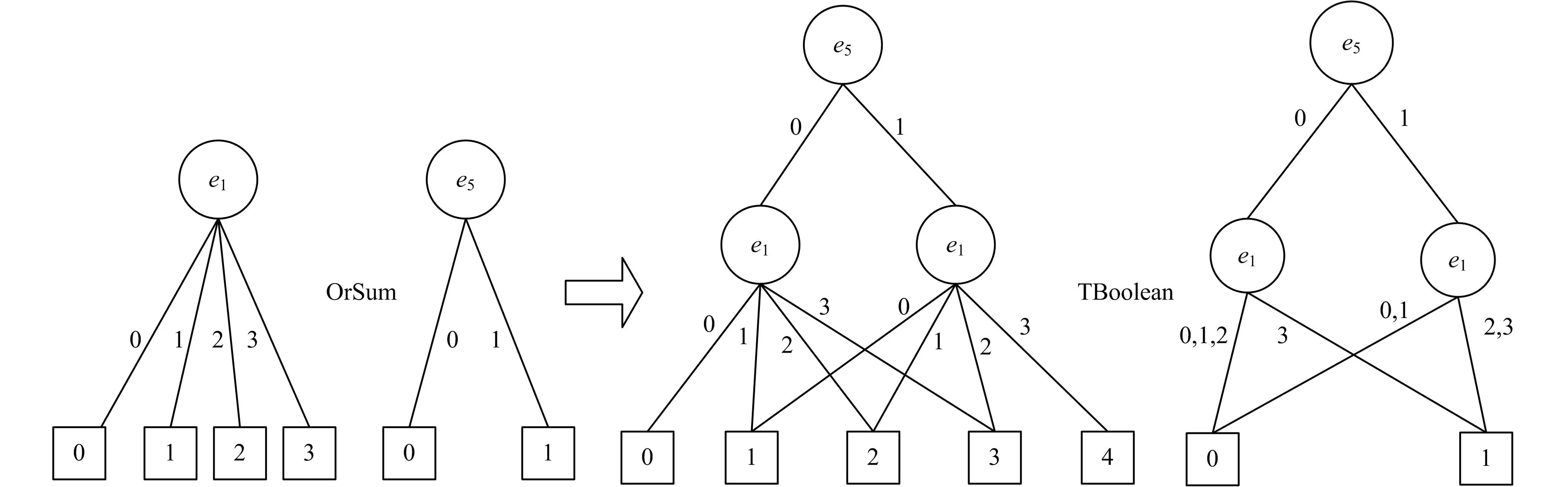
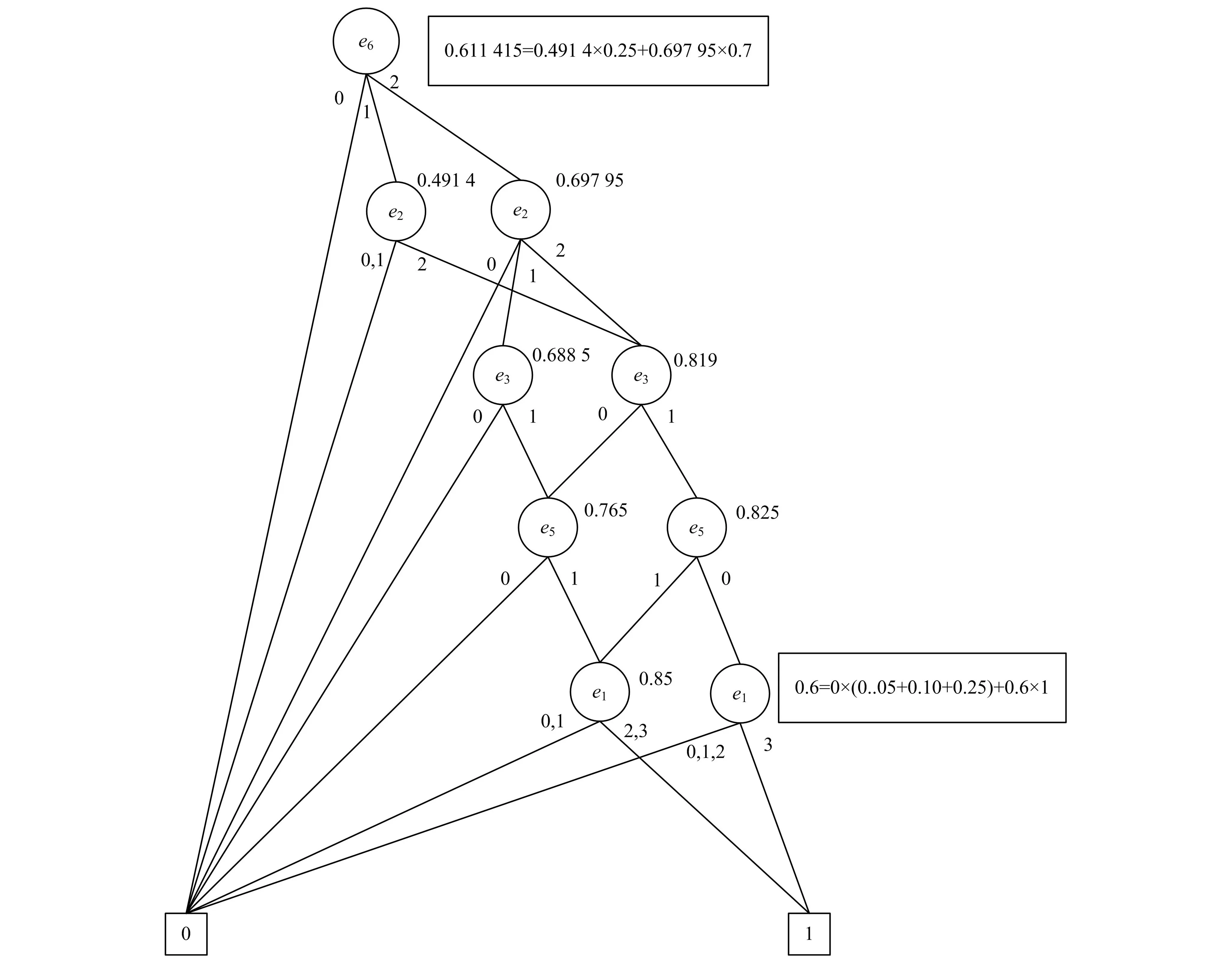
令wi表示边ei的当前流量,则wi的取值范围为0=ci0 针对多状态二端网络进行可靠性分析,问题的定义基于如下假设: 1)节点是可靠的; 2)每条边的容量以一定的概率随机分布; 3)每条边的容量相互独立; 4)遵循流量守恒定律。 最大流问题是运筹学和网络分析的一个标准问题,最小割和最大流是一对对偶问题。针对边上有多种整型容量的多状态网络,为了评估通过该网络最大流不小于给定的需求水平d的概率,给出如下最大流最小割定理。 定理1若一个多状态网络的最小割集为{K1,K2,…,Kq},则从源点s到终点t的最大流Fmax等于所有割中的最小流量: (1) 1.2多值离散概率模型MDD_ WS2TR MDD是一个多终端的有向无环图形化数据结构[12],表示一个多值输入与输出的离散函数F,如式(2)。针对多状态网络G,其离散概率模型MDD_WS2TR用MDD结构表示,如图1所示。网络的每条边都相当于一个多值变量,输出的值代表每个状态下对应的流量。 图1 MDD_WS2TRFig.1 MDD_WS2TR (2) 其中:Di={0,1,…,mi}为变量ei的取值范围;S={0,1,…,m}为函数的输出集合。 1.2.1操作算子 为了构建网络的MDD,定义OrSum、AndMin、TBoolean三个操作算子。依据最大流最小割思想,OrSum用于合并最小割内的边,对最小割内边上的流量求和;AndMin用于合并最小割,取所有最小割中最小的流量;TBoolean用于将每个最小割的MDD转换为布尔类型(终节点只有0或1),该操作可以简化MDD结构,将状态空间进一步压缩,减少节点个数,压缩了状态空间。此外,将该操作用于OrSum之后,在算法执行过程中使用,降低了AndMin操作的复杂度,提高了算法的执行效率。各操作算子的操作规则如表1所示。 表1 OrSum、AndMin、 TBoolean操作规则 1.2.2计算可靠度 通过操作算子构建网络的MDD,在生成了网络的MDD结构后,通过递归方法: (3) 遍历所有的节点求可靠度P(F),遍历过程只需要自顶而下遍历一次,时间复杂度为O(n),其中n为生成的MDD节点个数。 寻找最小割是一个NP-hard问题[11],求解最优变量序是一个NP-complete问题[13]。所以,预先求出最小割集和变量序,基于此,提出了评估多状态网络二端可靠性的MFMC_MDD算法。假设最小割集为{K1,K2,…,Kq},算法的执行步骤分为2步: 1)将预先求出的最小割集存于邻接表中,依次访问最小割Ki中的每一条边ei,并利用操作算子OrSum合并Ki中的每条边的MDD,从而构建出最小割Ki的MDD;通过TBoolean算子对Ki的MDD进行剪枝,进而简化为布尔类型;利用操作算子AndMin合并所有最小割的MDD,进而生成整个网络的MDD。伪代码为: 2)自顶而下递归遍历生成的网络MDD,利用式(3)求网络的可靠度。伪代码为: 为了简单直观地阐述MFMC_MDD算法,以图2作为基准测试网络对算法进行分析。通过求解该基准网络的二端可靠性,边上有若干随机的整型容量,说明了MFMC_MDD算法的计算过程,验证了算法的可行性。测试网络各个边上的数据如表2所示。 图2 测试网络Fig.2 Test network 边状态状态概率e101230.05550.100.250.60e2012-0.10000.300.60-e301--0.10000.90--e401--0.10000.90--e501--0.10000.90--e6012-0.05000.250.70- 已知需求水平d=3,最小割集MCs为: 变量序为: 求网络的最大流不小于3的概率。求解步骤为: 1)利用操作算子OrSum依次构建最小割K1、K2、K3、K4的MDD;通过算子TBoolean对最小割Ki的MDD进行剪枝,进一步缩减状态空间;再利用操作算子AndMin合并这些最小割的MDD,生成网络的最终MDD。图3为最小割K1的MDD。图4为最终生成的多状态网络MDD,节点旁的数字代表可靠度,方框中为计算方法,顶端的节点可靠度为整个网络的可靠度。 图3 K1的MDDFig.3 MDD of K1 图4 多状态网络的MDDFig.4 MDD of the multi-state network 2)遍历最终生成的MDD,求得需求水平d=3时的可靠度为0.611 415,与文献[1]中的可靠度一致。 为了验证MFMC_MDD算法的性能,从精确度、空间、时间3个方面对算法进行了测试。MFMC_MDD算法基于爱荷华州立大学开发的meddly库,实现语言为C++。实验环境为:Intel Xeon 2.13 GHz CPU,2 GB RAM,CentOS 5.5系统。 文献[4]对图2所示网络的边赋予了4组不同的概率值测试其可靠性,为了检验算法的正确性,同样使用文献[4]提供的4组数据对图2的网络可靠性进行测试。结果表明,得出的可靠性值与真实值完全一致,说明了MFMC_MDD算法能够精确计算多状态网络的二端可靠性。 为了检验MFMC_MDD算法的时间和空间性能,使用随机图生成器生成一组有向的随机流网络对算法进行测试,因为研究的是节点可靠的多状态网络,所以生成的这组网络均为10个节点,边分别为21、23、26、30。假设网络的边的容量分别为0、1、3,各个容量对应的概率分别为0.05、0.25、0.70。算法的测试结果如表3所示。实验结果表明:1)算法的执行时间依赖于需求水平d。其中,当状态空间达到330,d=1时,算法运行时间小于1 s;d=3时,算法运行时间小于90 s。2)随着需求水平d的增大,MDD的节点个数增多,但是与呈指数级的状态空间相比,MDD的节点个数少了很多,节省了大量的状态存储空间,与完全枚举法相比,MFMC_MDD算法是快速有效的。 表3 实验结果 计算多状态网络二端可靠性是一个典型的网络可靠性问题,针对该问题,提出了求解多状态二端可靠性的多值离散概率模型,并给出了MFMC_MDD算法。该算法基于最大流最小割思想来构建网络的MDD。通过OrSum操作算子对最小割中的边进行合并,构建最小割的MDD; TBoolean操作算子将最小割的MDD转换为布尔类型,对MDD进行剪枝,压缩了状态空间;AndMin算子对最小割进行合并,构建出整个网络的MDD。遍历网络的MDD,可以求得网络的可靠性。实验结果表明,MFMC_MDD算法可以精确有效地评估多状态网络的二端可靠性。 [1]JANE C C,LAIH Y W.Computing multi-state two-terminal reliability through critical arc states that interrupt demand[J].IEEE Transactions on Reliability, 2010,59(2):338-345. [2]DOULLIEZ P,JAMOULLE E.Tansportation networks with random arc capacities[J].Recherche Operationnelle, 1972,6(3):45-59. [3]ALEXOPOULOS C.A note on state-space decomposition methods for analyzing stochastic flow networks[J].IEEE Transactions on Reliability,1995,44(2):354-357. [4]RAMIREZ-MARQUEZ J E,COIT D W.A Monte-Carlo simulation approach for approximating multi-state two-terminal reliability[J].Reliability Engineering and System Safety,2005,87(2):253-264. [5]YEH W C.A simple MC-based algorithm for evaluating reliability of stochastic-flow network with unreliable nodes[J].Reliability Engineering and System Safety,2004, 83(1):47-55. [6]YEH W C.A novel method for the network reliability in terms of capacitated-minimum-paths without knowing minimum-paths in advance[J].Journal of the Operational Research Society,2005,56(10):1235-1240. [7]LIN Y K.Using minimal cuts to evaluate the system reliability of a stochastic-flow network with failures at nodes and arcs[J].Reliability Engineering and System Safety,2002,75(1):41-46. [8]LIN Y K.Reliability of a stochastic-flow network with unreliable branches and nodes,under budget constraints[J]. IEEE Transactions on Reliability,2004,53(3):381-387. [9]LIN Y K.System reliability evaluation for a multistate supply chain network with failure nodes using minimal paths[J].IEEE Transactions on Reliability,2009,58(1): 34-40. [10]LIN Y K.A simple algorithm for reliability evaluation of a stochastic-flow network with node failure[J].Computers and Operations Research,2001,28(13):1277-1285. [11]JANE C C,LAIH Y W.A practical algorithm for computing multi-state two-terminal reliability[J].IEEE Transactions on Reliability,2008,57(2):295-302. [12]SRINIVASAN A,HAM T,MALIK S,et al.Algorithms for discrete function manipulation[C]//IEEE International Conference on Computer-Aided Design,1990:92-95. [13]BOLLIG B,WEGENER I.Improving the variable ordering of OBDDs is NP-complete[J].IEEE Transactions on Computers,1996,45(9):993-1002. 编辑:梁王欢 An MDD-based algorithm for computing multi-state two-terminal reliability GUO Xiaoyong, DONG Rongsheng, ZHU Yangyang (School of Computer and Information Security, Guilin University of Electronic Technology, Guilin 541004, China) In order to compute the multi-state two-terminal reliability, a multi-valued discrete probability model MDD_WS2TR is defined. MFMC_MDD algorithm based on max-flow min-cut theorem is proposed, which combines the edges in the minimal cuts without considering the insignificant edge in the dense network. Especially, in the process of building MDD of the network, the operator TBoolean is defined to prune the MDD. Then the state space is compressed and the complexity of merging MDD is reduced. Finally MFMC_MDD algorithm is tested on a group of stochastic flow networks. The experimental results show that the proposed algorithm is effective. multi-state; maximum flow; minimal cut; MDD; reliability 2015-12-29 国家自然科学基金(61363070) 董荣胜(1965-),男,湖北黄冈人,教授,研究方向为计算思维、网络可靠性、形式化技术。E-mail:ccrsdong@guet.edu.cn TP302.7 A 1673-808X(2016)04-0305-06 引文格式:郭晓勇,董荣胜,朱阳阳.基于MDD的多状态网络二端可靠性算法[J].桂林电子科技大学学报,2016,36(4):305-310.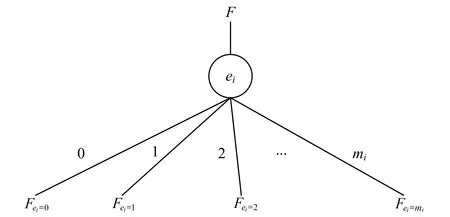

2 算法设计


3 实例分析

4 实验结果及分析

5 结束语

