第四讲 回归分析中的变量筛选技术及统计检验
徐静安 徐淑惠
技术讲坛
第四讲回归分析中的变量筛选技术及统计检验
徐静安徐淑惠
回归分析中的变量筛选技术是回归分析技术得到广泛应用的一个突破,它将方差分析中的F检验和回归分析技术进行集成,形成一个新的算法,为工程应用开拓了广泛的前景。
在笔者藏书中,涉及回归分析中变量筛选技术的专著有:《概率统计计算》(中国科学院计算中心概率统计组编著,科学出版社,1979);《回归分析及其试验设计》(上海师范大学数学系概率统计教研组编,上海教育出版社,1978);《回归分析方法》(中国科学院数学研究所数理统计组编,科学出版社,1974);《试验优化技术》(任露泉主编,机械工业出版社,1987);《应用回归分析》(盛承懋、李慧芬、钱君燕编译,上海科学技术文献出版社,1989);《技术数理统计方法》(曾秋成编著,安徽科学技术出版社,1982);《均匀设计与均匀设计表》(方开泰著,科学出版社,1994);《正交与均匀试验设计》(方开泰、马长兴著,科学出版社,2001);《生物统计学》(李春喜、姜丽娜、邵云、王文林编著,科学出版社,2005)。
上述专著讨论变量筛选技术均采用逐步回归法,从逐步回归的基本思想、数学模型、线性代数、计算框架、源程序等不同角度加以描述,各有侧重。对于非应用数学专业的工程技术人员,其遇到的困难可能在线性代数方面。20世纪70年代末笔者自学,初次接触矩阵转置、求逆……时,也是“一头雾水”。为了知道一点“所以然”,自行编写程序,进行工程应用,花了不少时间、精力学习线性代数。
新世纪,随着数据处理软件的推广应用,逐步回归法筛选变量技术得到进一步的普及应用,现已不需要自行编写计算程序,所以从应用角度推荐水泥凝固放热的案例,资料摘录自《六西格玛管理统计指南——MINITAB使用指导》(马逢时、周暐、刘传冰编著,中国人民大学出版社,2007)。
该案例是著名统计学家Hald于1952年给出的,被多本专著引用,采用不同的软件计算,结果相同。该案例把逐步回归的基本思想、自变量的筛选过程、回归模型的评价等描述得比较清晰,所以本文仅作简单解读。
一、案例简介

计算响应值y的发热量。
13组不同成分组合水泥凝固时的发热量数据见表1。首先要对自变量有专业的认识,自变量之间可能存在相关性。
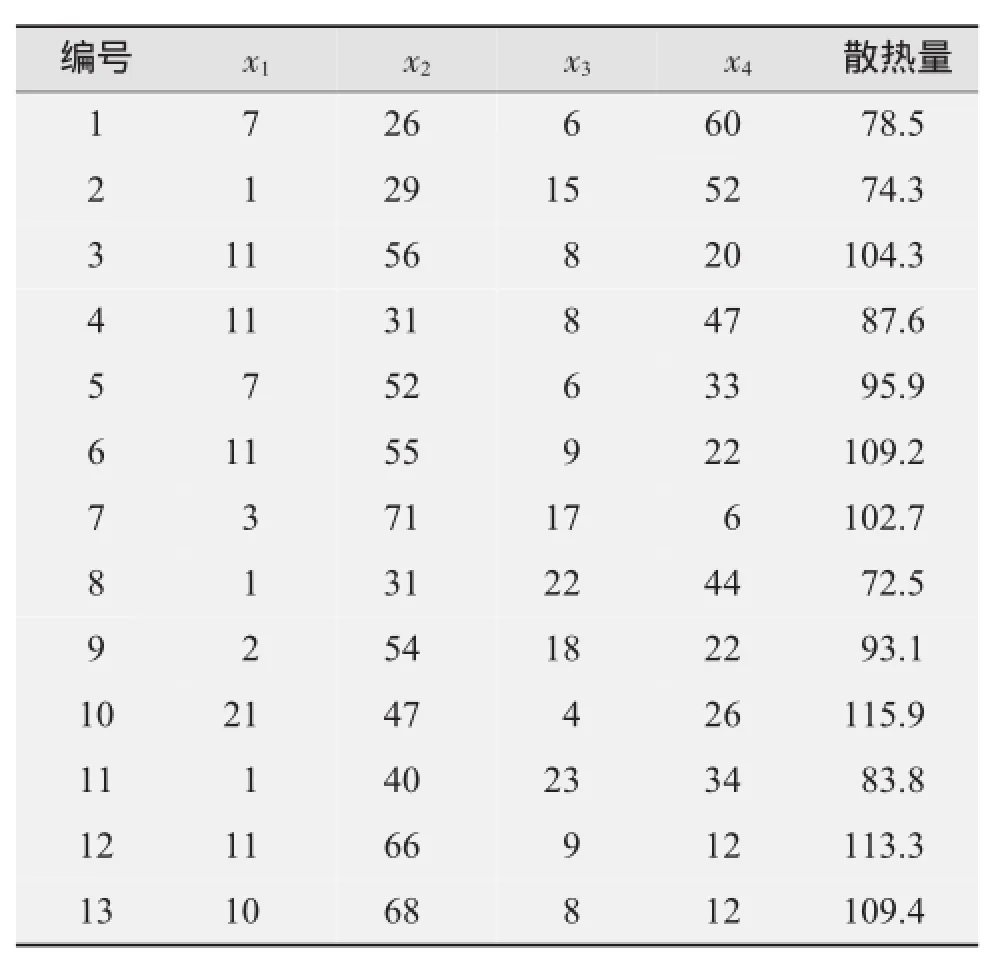
表1 不同成分组合水泥凝固时散热量数据记录
方法一:采用一般的多元回归分析方法
线性全回归方程为:
散热量=62.4+1.55x1+0.510x2+0.102x3-0.144x4回归系数显著性检验:

回归总效果度量:

回归方程显著性检验:

从对回归方程的显著性检验结果来看,P值=0<α=0.05,说明回归方程总效果是显著的。但从回归系数检验输出来看,自变量x1,x2,x3,x4的P值都大于α=0.05,都不显著,这就牵涉到如何分析各回归变量系数检验结果的问题。在各回归变量的系数检验中,P>0.05为不显著,相对应变量x应予删除,而不进入统计模型。本例先删除x3,又删除x4,修整后回归方程为:
散热量=52.6+1.47x1+0.662x2

方法二:采用逐步回归法
逐步回归分析方法的基本思想就是让计算机参与多元回归分析中的自变量筛选工作。筛选的方法有三种:
(1)“向前选择法”。思路是:逐个引入自变量,先选入对y影响最大(P值最小)者,再从其余自变量中寻找影响次最大(P值次最小)者,直到无任何变量P值小于指定的“选入α值”可以被引入为止。在向前选择方法中,自变量一旦被加进回归模型就不再被删除。
(2)“向后消除法”。思路是:一开始引入全部自变量,对于P值大于指定的“删除α值”者,进行逐个删除,直至不能再删除为止(该方法就如同方法一的修整)。
(3)“逐步法(向前和向后)”。思路是:自变量逐个引入,边引入边检查已引入自变量中最大的P值是否已大于指定的“删除α值”,若大于,则从模型中删除该项,再重复上述过程。如果没有任何自变量可以删除,则会尝试再加入一个新的自变量,重复上述过程,直至不能再引入乜不能再删除为止。
分析证明,几种方法的最终结果可能略有不同,以逐步法为最优。该案例是采用MINITAB软件进行计算。
逐步回归:散热量与x1,x2,x3,x4
入选用Alpha:0.15;删除用Alpha:0.15(计算机默认)
响应为4个自变量上的散热量,N=13
二、案例解读
原案例采用多元线性(一次项)回归方法,对计算机输出解读非常重要、非常精彩,值得一读,本文不重复。现对回归方程显著性检验、回归总效果度量、回归系数、显著性检验的相关指标进行说明(数据取自方法一线性全回归模型)。
(1)P值一般和显著性水平一致,取其值为α=0.05,0.01,P>0.05,不显著。
(2)回归方程的方差为:

按回归方程变量自由度DFA=4,误差自由度DFE=8,查F分布表,其相应临界值为:,高度显著。
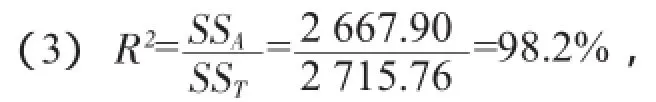
R(2决定系数)是传统回归总效果变量值,其临界值也可查相关系数临界值表。
回归方程自变量个数m=4,样本量n=13,

查表得R=0.811,R2=0.652<0.982,回归方程有显著意义。

此处P为进入模型的变量个数(包括常数项)。当前,度量回归模型的拟合效果时,很看重R2(调整)值,它能反映模型总项数的影响。

此处,S为回归方程拟合残差标准差。
概念上,在同类型回归模型拟合时,希望S越小越好;数量上,它是上述讨论的各指标中唯一没有临界值的一个指标。但相对指标还是有的,由于正态分布的误差,在(y±2S)范围内包含95%的数据;同时变异系数,不同专业有不同的要求,本案例为CV=2%~4%,可以接受。
(6)该案例回归总效果变量、回归方程显著性检验均有显著性意义,但自变量回归系数显著性检验均不显著,原因在于自变量之间存在相关性。相关分析:x1,x2,x3,x4

结果说明:x1与x3,x2与x4都高度负相关,原本在4个变量都包含在方程中时,删除任何一个变量对整个方程的影响都不大,但删除x3之后,x1就是显著的了;同理,删除x4之后,x2可能就显著了。
从案例的相关分析可以看出,X1与X3相关系数r=-0.824、P值=0.001<0.05;X2与X4的相关系数r=-0.973、P值=0,都是高度显著负相关。相关分析结果和化学组分的专业认识是一致的。
三、求取“最优”回归模型解析
1从所有可能的变量组合中人工挑选最优我们首先估计工作量,本案例有4个变量。如果按普适性的二次多项式考虑,可形成项,可能形成的回归方程有214-1=16 383个组合,事实上难以操作。案例根据经验只考虑一次项的多项式回归,可能形成24-1=15个回归方程。计算结果见资料《回归分析及其试验设计》、见表2。在15个方程中σ2=S2=MSE最小的为第12个方程,但b2有一定的影响,b4不显著,经过综合检验,确定第5个方程为“最优”。

2逐个删除不显著变量
案例方法一很清晰地演示、解读了删除过程,得到了:
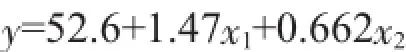
这里需要强调指出的是,如果按普适性的二次多项式考虑,形成m=14大于实验样本量n=13,就无法进行逐个删除。案例仅考虑一次项m=4,小于n=13,可逐个删除不显著变量。
由此可以看出,如果自变量较多,再考虑二次多项式,人工逐个删除不显著变量的工作量也是非常大的。

表2 考虑一次项的多项式回归方程计算结果
3采用逐步回归法
前进法是“只进不出”,后退法是“只出不进”,在自变量相关性复杂的情况下,还是“有进有出”的逐步法为优选。
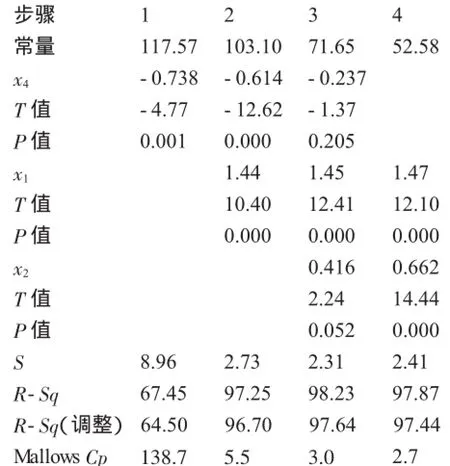
MINITAB软件在逐步回归计算结果输出时,有一个Mallows Cp值。该值以接近进入模型的变量项数(包括常数项)为好。
案例采用逐步回归法,Mallows Cp值的变化为138.7→5.5→3.0→2.7,此时进入模型的量有x1,x2及常数项共3项,Cp值最为接近。Cp值可以辅助判断变量的引入或删除。
案例采用前进法、后退法及逐步法时,选用了不同的引入、删除变量F检验的显著性水平α值,分别为0.25,0.10,0.15,事实上不同软件设置的默认值也不相同。但是不影响回归方程显著性及回归系数显著性检验时,公认的标准为p=α≤0.05。
对于离散性较大的工程数据、宏观统计数据,也有α=0.10的报道。
逐步回归法获得模型y=52.58+1.47x1+0.662x2,结果见表3。
为了进一步的讨论,笔者和在读研究生徐淑惠同学采用DPS软件进行计算、解读。

表3 DPS逐步回归法计算结果
四、用DPS软件进行验证性计算
点击:多元分析——回归分析——逐步回归,计算输出结果和MINITAB等计算结果一致。
需要说明的是:
(1)DPS系统在逐步回归计算时,采用浮动Fα临界值的方法,计算软件自动调整Fα值以保证选入一个自变量因子。然后软件在α=0.10条件下逐步引入或剔除变量。
如果入选的自变量数目不多,可以人为干预降低引入门槛,如在α=0.15等条件下筛选变量,反之亦然。
(2)DPS系统在逐步回归计算输出时,除了①回归系数显著性检验;②回归总效果变量;③回归方程显著性检验;还给出了④拟合误差(残差)表。在统计检验具有显著性意义的前提下,由拟合误差表可以大致分析出是否存在可疑的异常点、特殊地位的杠杆点,以免影响模型的稳定性。本案例拟合误差最大的样本6拟合误差的绝对值为4.047 5<2~2.5 S,且CV=s=2%~4%,相对于本模型观察数据y¯正常。如果不正常,则需要进行进一步的分析讨论。
(3)DPS系统在逐步回归计算输出时,还输出了Durbin-Watson统计量d,这是当前回归分析统计检验中残差诊断的一个重要统计量(0<d<4)。如果d接近0,表示残差存在正相关;d接近4,表示残差存在负相关;d接近2,表示残差相互独立。本案例d=1.92,模型正常。如果不正常,就要对自变量进行变换,修正模型,如选用高次方程等。结果见表4。
五、模型预测结果的整体估计
讨论解读至此,本文的重点是在多元回归分析中如何采用一种较优的方法——逐步回归法筛选因子变量,获得“最优”的回归统计模型。多项统计检验证明,本模型是有显著性意义的、正常的、合理的。这些讨论解读还只是局限在模型对实验观察值的拟合效果范围内的。我们求取统计模型(求取理论模型、半经验模型的相应系数)的目的一是求得极值,二是将模型用于控制或仿真,这均涉及到模型预测结果的整体估计。

表4 拟合结果
拟合不好的模型,预报效果一定不好;拟合好的模型,预测效果可能好,也可能不好。对于模型预测结果的整体估计Press及验证实验,另有案例讨论。此外,本案例统计建模没有混料配才约束∑xi=1,甚为可惜,另行专题讨论。

