穿透非均质储层的复杂轨迹井产量计算新方法
陈志海,董广为,廉培庆
(中国石化 石油勘探开发研究院,北京 100083)
穿透非均质储层的复杂轨迹井产量计算新方法
陈志海,董广为,廉培庆
(中国石化 石油勘探开发研究院,北京 100083)
解析法和半解析法计算水平井产量的公式一般要求油藏储层均质,且井轨迹平行于油藏边界,难以准确地计算复杂轨迹井的产量。根据井轨迹和储层渗透率把油藏划分为若干区域,不同区域渗透率取值不同,且井轨迹可不平行边界。通过引入点源函数法,基于定压油藏边界建立了非均质性储层复杂轨迹井的产量分段积分相似解,利用Ouyang模型计算了井筒内流动的沿程压力损失。该方法避免了数值模拟中数值弥散的发生,只需输入较少的参数就可以对复杂轨迹井进行快速产能评价。实例计算结果表明:①复杂轨迹井井筒内的流量从指端到跟端逐渐增大;②由于储层的非均质性,各段流量分布并不均匀,渗透率高的部位流量也高;③井筒压降从指端到跟端同样逐渐增大,由于流量分布不均匀,因此不同轨迹段在井筒内压降也不相等。该方法计算结果与Eclipse数模方法一致,表明该方法是可行的。应用该方法计算的油井产量与油田现场生产对比,预测油井产量相对误差小于5%,能满足现场油藏工程研究的需要。
非均质储层;点源函数;复杂轨迹井;产量计算
近十年来,复杂轨迹井开发技术在油气田开发领域取得突飞猛进的发展,已经由单一的水平段发展为极大限度接触油藏面积的复杂轨迹井段(又称复杂结构井技术)。该技术不仅在常规油气藏开发的剩余油挖潜应用广泛,而且已成为包括页岩油气、致密油气、深水油田等非常规油气藏开发不可或缺的主导技术之一[1-3]。现场实践表明,复杂轨迹井技术不仅能提高单井产量,而且能提高油田的采收率,使很多无法开发的油田获得经济有效地开发。复杂轨迹井与油藏接触面积大,克服油藏储层非均质性对油井产量的制约,实现单井经济效益最大化[4]。
目前,水平井已具有较为配套的单井产量计算公式包括计算定压边界油藏的稳态法和计算封闭边界油藏的拟稳态法。对于定压边界油藏水平井产量的经典公式主要包括Joshi 模型[5]、Bulter模型[6]、范子菲模型[7]和Furui模型[8]。Joshi 模型要求水平段长度相对于油藏边界长度小,即低穿透比能满足压力等势线呈椭圆形。其余几个模型要求水平段的穿透比为1,即满足垂直于水平段的流线相互平行地流入井筒。国内很多学者在这些模型基础上进一步推导了一些改进公式[9-12],这些公式的多假设油藏呈箱型、均质,且水平段与某一边界平行。
复杂轨迹井与传统水平井有很大的差异,主要体现在长井眼段与油藏接触,穿透多段非均质性储层,且在油藏内的井身轨迹复杂多变,此类井的产量计算未能得到较为满意地解决。国内很多学者也开展了很多探索,主要集中在结构简单水平井的井筒摩阻计算、多分支井间干扰、射孔方式对产量的影响等方面,但大多考虑单一因素对产量的影响[13-14]。考虑多因素对计算复杂轨迹井产量的方法在文献中比较少见。
1 复杂轨迹井流动模型建立
假定油藏形状为箱型,油藏上、下边界封闭,其余4个外边界定压(图1)。复杂结构井井眼轨迹在油藏内可以为任意曲线形状,沿程流动阻力不断发生变化。为精确地描述油藏流入井筒的渗流和井筒内的流体管流分布,依据油藏非均质性和井眼轨迹,将复杂轨迹井的井筒分段计算,使得每一微段井筒近似为直线并且考虑微井段对应储层的非均质性。
假定连续的井眼曲线轨迹可离散为N个微井段,第1个微段为复杂轨迹井的指端,而第N个微段为复杂轨迹井的跟端(图2)。每个微井段都能穿越对应油藏的非均质储层段,微井段的节点压力受井筒内沿程摩阻分布的影响,假设第i个井筒微段所在储层x,y,z方向渗透率分别为Kx,i,Ky,i,Kz,i,微段长度为Li,应井筒内流量为qi,井筒压力为pi。
每一微井段相当于一个独立的线汇,由一系列点汇连接而成。点汇位于井筒横截面圆心位置,并且过点汇的井筒横截面上压力均相等。因而点汇处的压力代表了和油藏接触的井筒外边界的油藏压力。在进行空间上的压力叠加时,考虑各微井段间相互干扰,则i个微井段的压力降为:pR-pi

图1 油藏与井筒物理模型示意图Fig.1 Reservoir and wellbore trajectory model

图2 非均质储层内复杂轨迹井的管流模型Fig.2 Pipe flow model of complex trajectory well in heterogeneous reservoirs

(1)式中:pR为油藏初始压力,MPa;pi为第i个微井段中心点压力,MPa;B为原油体积系数,m3/m3;qj为第j个微井段的流量,m3/d;a,b,h分别为模拟油藏的长、宽、高,m;Lj为第j个微井段的长度,m;Φ为孔隙度,%;Ct为综合压缩系数,MPa-1;xi,yi,zi为第i个微井段的中点坐标;lj为第j个微井段轨迹;t为生产时间,d;τ为时间积分变量。
公式(1)中G[(xi,yi,zi),lj,τ]为Green函数,根据Newmann积原理可以表示
(3)
(4)

以y方向为例,介绍Green函数的简化过程。把Green函数代入公式(1),可得:
(6)
对于拟稳态状态下的流动,令t→∞,可得:
(7)
方便起见,令Aij为第j个微井段对第i个微井段中心点的影响因子:
(8)
则公式(7)可表达为:
(9)
公式(9)矩阵表达式为:

井筒内流体流动存在摩阻,考虑重力、粘滞摩阻和加速度摩阻的影响,目前许多学者开展了井筒压降模型的研究[17-19]。本文采用Ouyang单相模型计算由重力、摩擦、加速度3部分构成的压降,并通过摩擦系数经验修正公式融入了射孔粗糙度造成的压降。压降方程表达式为:
译者是翻译的主体,也是民族文化建构的重要参与者。从功能角度看,中国文化外译属于外宣翻译。在外宣翻译中,译者的主体性体现尤为重要,因为中国在国际社会的形象很大程度上取决于外宣翻译的质量(张健,2013)。为达到传播和接受效果,需要译者在翻译过程中时刻考虑目标读者的阅读感受。在中国文化外译过程中,译者主体性影响、制约和支配着文化翻译的效果。

(11)

fj为第j微井段摩阻因子,无因次,可表示如下:
(12)
式中:f0为没有流体流入时摩阻因子,无因次;qI为单位长度的流量,m2/d;D为井筒直径,m;NRe,NRe,w分别为雷诺数和流入雷诺数,无因次。
因此,井筒内部每两个相邻微井段中心点之间的压降,可以由Ouyang模型算得,数学表达式为:
(13)
代入前一方程组可得以下矩阵形式:
(14)
当井底流压给定,此方程组为关于(q1,q2,…,qN)的非线性方程组,可由Newton-Raphson迭代法求解。
2 应用实例
安哥拉某深水油田浊积岩油藏为渗透率各向异性的非均质油藏,油藏上、下边界封闭,四周为边底水定压边界,压力值为16.55 MPa。油藏长度1 524 m,宽度为610 m,有效厚度为61 m。复杂轨迹井在油藏内裸眼段井筒长1 219 m,跟端井底流压为13.79 MPa,沿井筒轨迹穿越油藏储层的渗透率分布如表1所示,井筒粗糙度0.000 6,其他参数见表1。
2.1井筒流量及压力分布
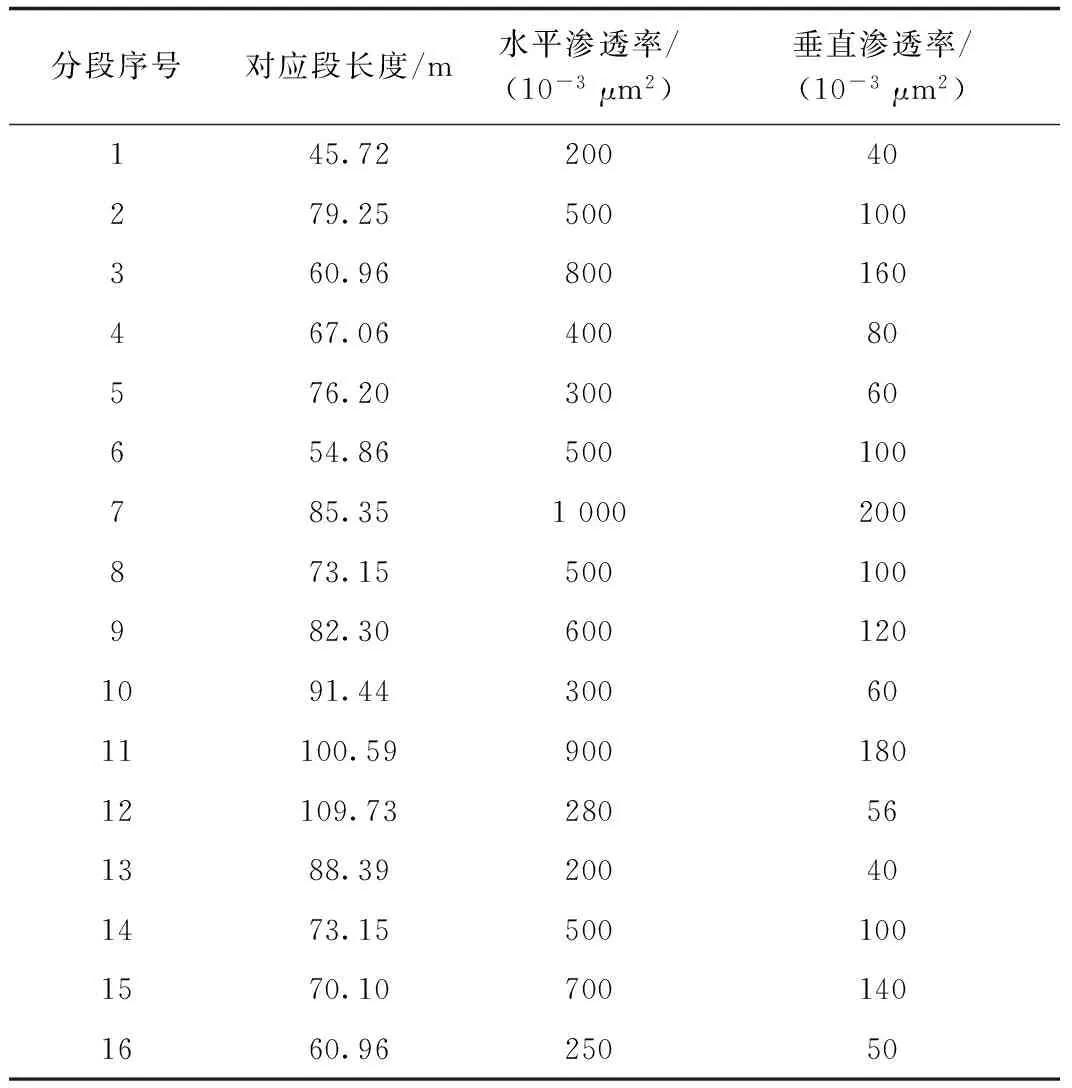
表1 各井段长度和渗透率
对于长井段复杂轨迹井,考虑渗透率差异性,分段赋值计算从油藏流入井筒的流量,并沿程计算井筒摩阻压降对产量的影响是必要的。该计算方法能够更准确地计算复杂轨迹井的产量,更好地考虑工程和地质的需要。
2.2与Eclipse结果对比
采用相同油藏、流体和复杂轨迹井参数,对比了该方法计算结果和Eclipse软件计算结果,由图5可知,各节点的流量与渗透率值呈现正相关性,计算结果与Eclipse模拟结果基本一致,井筒中间段较好吻合,两端吻合稍差,Eclipse结果偏低,这是因为Eclipse设定的边界条件难以满足定压边界,更接近于封闭边界。
点源函数法的优势在于避免了数值模拟中数值弥散的发生,只需输入较少的参数就可以对复杂轨迹井进行快速产能评价。而油藏数值模拟方法的数值发散现象,以及需要输入较为准确的油藏参数,限制了该方法在油藏评价阶段的应用。

图3 分段流入量及累计流入量分布Fig.3 Inflow rate of different segments and cumulative pipe flow rate

图4 分段井筒摩阻压降及累计压降分布Fig.4 Pipe flow pressure drop of different segments and cumulative pressure drop

图5 点源函数与数模方法结果对比Fig.5 Results comparison between point source function method and Eclipse simulation
2.3计算结果与油田现场对比
应用该方法计算了安哥拉某深水油田A1井在不同井底流压下的产量(图6),井底流压越小,生产压差越大,单井日产油量也就越高。通过与油田现场测量的产量数据进行对比可以看出,预测的油井产量稍低于实际产量,这主要是模型做了简化造成的,但总体相对误差小于5%,能满足现场油藏工程研究的需要。

图6 新方法计算产量与现场产量对比Fig.6 Comparison of the calculated well production rate with the metered oil production in oilfield
3 结论与认识
应用点源函数方法计算复杂轨迹井产量,不仅考虑了油藏储层的非均质性和沿程井筒的压降损失,而且适用条件和应用范围更广,克服了传统水平井产量计算方法的不足。通过计算实例表明,该方法能准确地计算复杂轨迹井的产量,在油藏评价阶段能发挥快速便捷的作用。通过与油藏数值模拟结果对比,表明该方法是切实可行的。
[1]Lian Peiqing,Cheng Linsong,Tan Xuequn,et al.A reservoir/wellbore coupling flow model for fishbone wells[J].Petroleum Science,2012,9(3):336-342.
[2]李龙龙,姚军,李阳,等.分段多簇压裂水平井产能计算及其分布规律[J].石油勘探与开发,2014,41(4):457-461.
Li Longlong,Yao Yun,Li Yang,et al.Productivity calculation and distribution of staged multi-cluster fractured horizontal wells[J].Petroleum Exploration and Development,2014,41(4):457-461.
[3]苏玉亮,王文东,周诗雨,等.体积压裂水平井三线性流模型与布缝策略[J].石油与天然气地质,2014,35(3):435-440.
Su Yuliang,Wang Wendong,Zhou Shiyu,et al.Trilinear flow model and fracture arrangement of volume-fractured horizontal well[J].Oil & Gas Geology,2014,35(3):435-440.
[4]陈卫东,Hill A D.多分支井产能预测方法[J].中国海上油气,2006,18(6):394-396.
Chen W D,Hill A D.Development of multilateral well deliverability model [J].China Offshore Oil and Gas,2006,18(6):394-396.
[5]Joshi S D.Augmentation of well productivity using slant and horizontal wells[J].Journal of Petroleum Technology,1988,40(6):729-739.
[6]Butler R M.Horizontal wells for the recovery of oil,gas and bitumen[M].Australia:Petroleum Society of CIM,1996:121-135.
[7]范子菲,林志芳.边水驱油藏水平井产能公式研究[J].大庆石油地质与开发,1994,18(2):55-62.
Fan Zifei,Lin Zhifang.Productivity formula of horizontal well in
reservoirs with edge water drive [J].Petroleum Geology & Oilfield Development in Daqing,1994,18(2):55-62.
[8]Furui K,Zhu D,Hill A D.A rigorous formation damage skin factor and reservoir inflow model for a horizontal well[J].SPE Production & Facilities,2002,18(18):151-157.
[9]韩国庆,吴晓东,陈昊,等.多层非均质油藏双分支井产能影响因素分析[J].石油大学学报,2004,28(4):81-85.
Han Guoqing,Wu Xiaodong,Chen Hao,et al.Influence factors for production of dual-lateral well in multilayer heterogeneous reservoir [J].Journal of the University of Petroleum,China,2004,28(4):81-85.
[10]廉培庆,程林松,张继龙,等.考虑表皮影响的底水油藏水平井非稳态流动分析[J].石油钻探技术,2010,38(4):94-98.
Lian Peiqing,Cheng Linsong,Zhang Jilong,et al.Analysis of horizontal well flow with skin effect in bottom water driven reservoir[J].Petroleum Drilling Techniques,2010,38(4):94-98.
[11]廉培庆,陈志海,董广为,等.水平井与非均质盒式油藏耦合模型[J].深圳大学学报理工版,2015,32(3):266-271.
Lian Peiqing,Chen Zhihai,Dong Guangwei,et al.A coupling model for horizontal well in heterogeneous box-shaped reservoir [J].Journal of Shenzhen University Science and Engineering,2015,32(3):266-271.
[12]曾凡辉,郭建春,尹建.井筒与油藏耦合的压裂水平井非稳态产能计算模型[J].现代地质,2011,25(6):1159-1166.
Zeng Fanhui,Guo Jianchun,Yin Jian.An unsteady state computation model of fractured horizontal well coupling with reservoir[J].Geos-cience,2011,25(6):1159-1166.
[13]何军,范子菲,赵伦,等.点汇离散法在压裂水平井产能评价中的应用[J].天然气地球科学,2016,27(1):134-141.
He Jun,Fan Zifei,Zhao Lun,et al.Application of point sink discretization in the productivity evaluation of fracture horizontal well[J].Natural Gas Geoscience,2016,27(1):134-141.
[14]Dong Guangwei,Chen Zhihai,Lian Peiqing.Calculation method on complex-structure well rate in heterogeneous reservoirs with constant pressure boundary[C]//International Conference on Reservoir Surveillance and Management.Beijing:2014:1-10.
[15]Gringarten A C,Ramey H J.The use of source and green’s functions in solving unsteady-flow problems in reservoirs”[J].SPE Journal,1973,13(5):285-296.
[16]刘波涛,李清泉,张福祥,等.致密油藏多级压裂水平裂缝井不稳态产能分析[J].石油与天然气地质,2014,35(1):138-142.
Liu Botao,Li Qingquan,Zhang Fuxiang,et al.Rate transient analysis of multistage fractured wells with horizontal fractures in tight oil reservoirs[J].Oil & Gas Geology,2014,35(1):138-142.
[17]Ouyang L B,Arbabi S,Aziz K.General wellbore flow model for horizontal,vertical and slanted well completions[J].SPE Journal,1998,2(2):124-133.
[18]Ouyang L B,Thomas L K,Evans C E,et al.Simple but accurate equations for wellbore pressure drawdown calculation[C]//SPE Western Regional Meeting,1997:1-14.
[19]刘想平,张召顺,刘翔鹗,等.水平井筒内与渗流耦合的流动压降计算模型[J].西南石油学院学报,2000,22,(2):36-39.
Liu Xingping,Zhang Zhaoshun,Liu Xiange,et al.The pressure drop calculating model coupling flow in the horizontal wellbore with fluid flow in reservoirs [J].Journal of Southwest Petroleum Institute,2000,22(2):36-39.
(编辑张亚雄)
A new method for production calculation of complex trajectory wells in heterogeneous reservoir
Chen Zhihai, Dong Guangwei, Lian Peiqing
(Exploration&ProductionResearchInstitute,SINOPEC,Beijing,100083,China)
Analytical and semi-analytical formulas for production calculation of horizontal wells generally require the reservoirs being homogeneous and well trajectory parallel reservoir boundary,which make them unsuitable for complex trajectory wells.In this paper,the reservoir is divided into several regions based on well trajectory and permeability.Each region has different permeability,and the well trajectory within the region may be unparallel with the boundary.The point source function method is introduced to establish the segmented integral similarity solution for the production of complex-trajectory well in heterogeneous and constant-pressure-boundary reservoir,and the Ouyang model is used to calculate the pressure loss along the wellbore.This method can avoid numerical dispersion in simulation,and provide a fast production evaluation with fewer input parameters.Case study result shows that flow rate in wellbore with complex trajectory increases from toe to heel,the reservoir inflow rate is different in each segment due to reservoir heterogeneity and is high in the high permeability reservoir region,the pressure drop within the wellbore also increases from toe to heel and is different in each wellbore segment due to the uneven distribution of flow rate.The result of this method is consistent with that of Eclipse,confirming its feasibility.In comparison with the metered oil production in field,the calculated production of complex trajectory well has an error of less than 5%,showing that it can satisfy the demand of real-field reservoir engineering research.
heterogeneous reservoir,point-source function,complex-trajectory well,production calculation
2015-02-13;
2016-04-15。
陈志海(1970—),男,博士、教授级高级工程师,油气藏渗流理论及数值模拟。E-mail:chenzh.syky@sinopec.com。
国家科技重大专项(2016ZX05033-003);中石化科技部项目(P12100)。
0253-9985(2016)03-0444-06
10.11743/ogg20160319
TE312
A

