永磁同步电机参数自动辨识方法研究

陈志锦，马艳

（中国兵器工业第58研究所 四川 绵阳 621000）

永磁同步电机参数自动辨识方法研究

陈志锦，马艳

（中国兵器工业第58研究所 四川 绵阳 621000）

针对不同电机参数上存在差异只适用于某种特定参数的交流伺服驱动器的特点，提出了一种基于Smith预估补偿和RBF神经网络与PID控制器相结合的永磁同步电机自动辨识控制算法。该方法利用了Smith预估补偿能克服纯滞后和RBF能处理非线性问题、在线自学习整定PID参数的优点，在调速模块的伺服控制系统中更加有效。通过系统建模和仿真实验结果表明，该算法能够有效辨识定子电阻、电感，并得到较为理想的实验结果。

永磁同步电机；Smith预估补偿；RBF神经网络；PID控制

伺服系统常用的电机类型有永磁直流电机、交流永磁同步电机、异步伺服电机等。交流永磁同步电机（permanent magnet synchronous motor，PMSM）具有体积小、质量轻、效率高、惯性低及转子无发热等优点，在伺服系统中得到广泛的应用。永磁同步电机在高精度位置伺服系统中应用广泛，传统上一般采用位置环、速度环和电流环的3环控制，控制器一般采用PID控制器或其改进型［1］。

目前，矢量控制技术使永磁同步电机越来越广泛地进入到高性能工业或军事应用领域中。矢量控制技术一般使用PI或者PID作为电流控制器，在矢量控制系统中，电流环是调速系统中响应最快的一环，其控制器参数的优劣将直接影响到整个调速系统的性能，而根据经典控制理论方法可知，对电流控制器参数影响最为直接的便是电机的定子电阻和电感［2］。电机的电阻和永磁体供磁能力会因为温度的变化而发生变化［3］；d-q轴电感值会因不同运行条件下电流变化所引起的不同程度磁饱和而发生变化［4］，这些参数的变化将导致电流控制器PI参数与实际运行条件不匹配，导致系统性能明显下降。因此，对电机参数进行准确的辨识将直接决定电流控制器控制性能的好坏，进而影响到整个系统的性能［5］。

由于不同电机在极对数、编码器线数和安装位置等参数上存在差异，通常的交流伺服驱动器只能适配固定型号或品牌的电机，当交流伺服系统采用新电机时，一般都需要重新烧写相应软件对电机参数进行修改。而具备电机自动辨识功能的交流伺服驱动器则可方便的对电机进行辨识并自动进行参数匹配及存储。

1 永磁同步电机调速系统数学模型

永磁同步电机调速如图1所示。由于电机转速的变化比电流的变化慢得多，可以认为电机电流在调节时，电机的转速是常数值，于是电机的电流环控制对象可以简化为如下的一阶惯性环节：

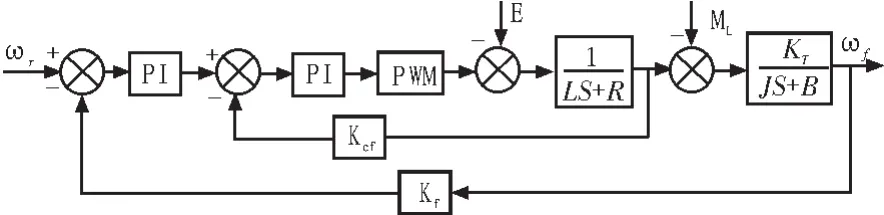
图1 永磁同步电机调速系统框图Fig.1 Speed control system diagram of PMSM

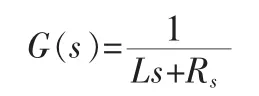
当电流环采用电流反馈解耦PI控制时，PI控制器的传递函数为：

如果取Ki/Kp=L/Rs，则闭环系统传递函数为：

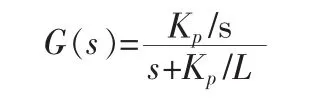
闭环传递函数还是为一阶惯性环节，其电流环的带宽Wb=Kp/L。

2 永磁同步电机参数自动辨识算法

2.1 RBF网络PID整定原理

RBF网整定PID控制参数采用增量式PID控制器，控制误差为：error（k）=rin（k）-yout（k）

神经元PID控制器的三项输入为：

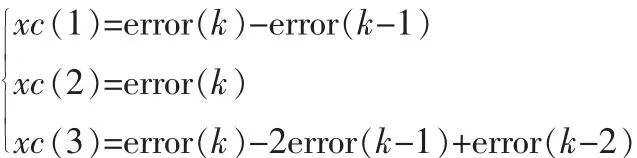
控制算法为：

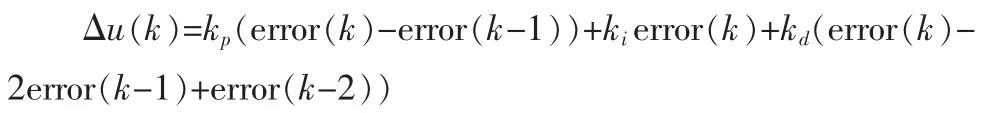
神经网络整定指标为：

kp，ki，kd的调整采用梯度下降法：

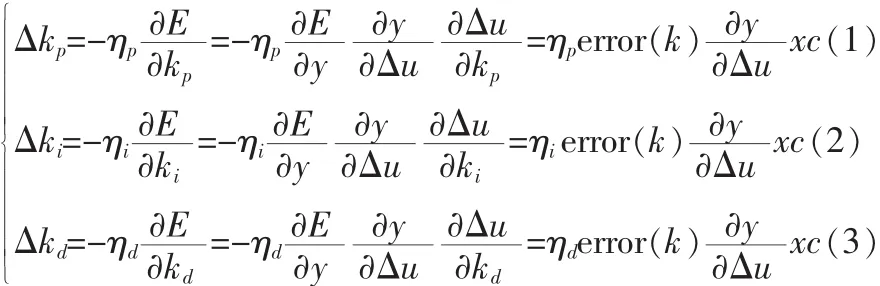
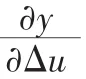
2.2 Smith预估补偿控制原理

Smith预估补偿控制系统框图如图2所示。Smith预估补偿是在PID控制器中引入预估补偿器DC（s），将其并联在控制器DC（s）上。其传递函数为：DC（s）=GC（s）（1-e-τms）。

图2 Smith预估补偿控制系统框图Fig.2 Control system diagram of Smith predictive compensation

图中虚线部分是带纯滞后补偿控制的控制器，其传递函数为

如果模型精确，可令其等于GC（s）=GP（s），τm=τ且不存在负荷扰动，r（s）=0，

经过纯滞后补偿控制后系统的闭环传递函数为

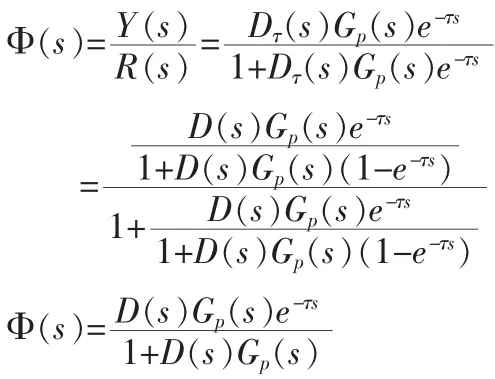
经补偿后，实现了将纯滞后环节移到闭环控制回路之外，纯滞后环节e-τs已经不出现在分母中，从而有效地消除了纯滞后对控制系统的影响。

2.3 Smith预估补偿与RBF神经网络PID控制算法

Smith预估补偿与RBF神经网络PID控制结构图如图3所示。利用RBF神经网络不依赖于控制对象的精确模型的优点和在线学习方法，利用Smith预估补偿器对纯滞后系统的良好控制，以及利用PID控制能实现小偏差范围内实现精确控制，达到优势互补的作用。

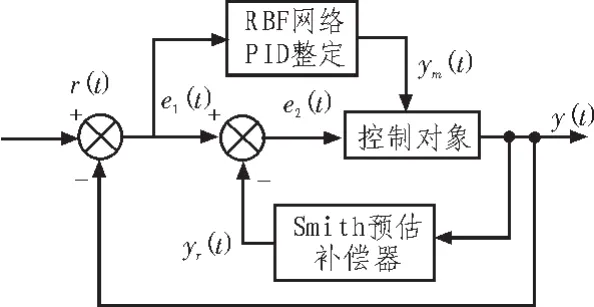
图3 Smith预估补偿与RBF神经网络PID控制框图Fig.3 Control diagram of Smith predictive compensation and RBF neural network setting PID

2.4 算法仿真

3 系统建模及仿真

本系统调用了Matlab/Simulink中的PMSM模块，功率电子IGBT模块，测量模块以及相关的控制模块来完成系统仿真平台的搭建。PMSM参数设置如表1所示。

根据仿真平台和上面介绍的辨识方法，依次对永磁同步电机的定子电阻、电感进行辨识，这样的辨识顺序可以保证每一个参数辨识完成后的电机状态、辨识结果可以为下一个参数的辨识提供依据和便利。

辨识定子电阻与电感过程中，由于避开了上下管交替开通关断的时刻，所以不存在死区效应，不需要对死区进行补偿。

图4 MATLAB仿真Fig.4 The simulation of MATLAB

表1 PMSM仿真参数Tab.1 The simulation parameters of PMSM

3.1 辨识定子电阻仿真实验

首先进行相对容易辨识的定子电阻参数辨识，验证前面的分析结论。

仿真系统直流母线电压为310 V，系统的开关频率为10 kHz。开始施加占空比为5%的电压矢量（1，0，0），这样一方面可以根据d轴电流为稳态值计算出定子电阻值，另外也确定了转子的位置。

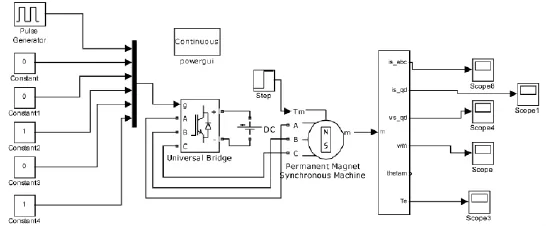
图5 参数辨识仿真模型Fig.5 Simulation model of parameter identification

在辨识电阻时主要关注电流的稳态波形，于是放大第一次上升过程后d轴电流的稳态波形得到图6。

由图可以看到由于施加PWM开关等效的电压矢量，稳态电流波形存在固定开关频率的抖动，于是对稳态波形增加一个滤波环节而得到一个较为平滑的电流稳态波形，如图7所示。

电流大小为3.9 A，可以得到定子电阻为：

这与真实结果相比误差为0.37%，比较微小。

图6 电流波形Fig.6 The current waveform

图7 平滑后电流波形Fig.7 The smooth current waveform

3.2 辨识定子电感仿真实验

在较为准确的辨识了电阻值之后进行电感的辨识。从图8中看到施加固定电压矢量使得电流达到稳态值从而辨识完定子电阻后，关闭PWM信号使得电流归零。然后在0.2 s时施加占空比为5%的电压矢量（1，0，0），观察d轴上升曲线，从而开始对定子电感进行辨识。

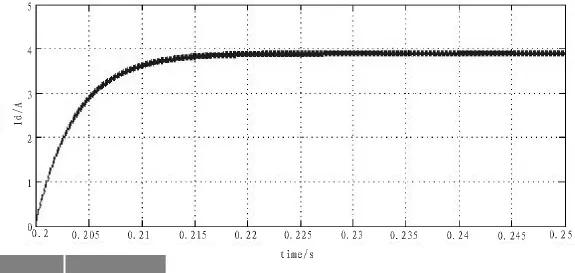
图8 上升波形Fig.8 The rising waveform

根据对电机模型的理论推导，这一上升曲线应为标准的指数曲线，时间常数为Ld/R，分别取不同时刻采样电流值计算定子电感：

结果误差都在2%以内，验证了之前理论推导的正确性。

4 结 论

文中提出一种基于Smith预估补偿与RBF神经网络PID控制算法的永磁电机参数自动辨识方法，通过系统建模和仿真实验结果表明，该算法能够有效辨识定子电阻、电感，并得到较为理想的实验结果。

［1］王宏，于泳，徐殿国.永磁同步电动机位置伺服系统［J］.中国电机工程学报，2004，24（7）:151-155.

［2］Antonio Visioli.Practical PID control［M］.London:Springer，2006.

［3］Wilson S D，Stewart P，Taylor B P.Methods ofresistance estimation in permanent magnet synchronousmotors for realtime thermal management［J］.IEEETransactions on Energy Conversion，2010，25（3）:698-707.

［4］Tilak Gopalarathnam，Roy Mc Cann.Saturation andarmature reaction effects in surface-mount PMACmotors［C］.IEEE International Conference on ElectricMachines and Drives，2001:618-621.

［5］杨立永，张云龙，陈智刚，等.基于参数辨识的PMSM电流环在线自适应控制方法 ［J］.电工技术学报，2012，27（3）：86-91.

［6］李兵强，吴春，林辉.基于参考输入学习的永磁同步电机高精度位置伺服系统［J］.中国电机工程学报，2012，32（3）：96-101.

［7］飞思科技产品研发中心.神经网络理论与MATLAB7实现［M］.北京：电子工业出版社，2002.

Research on parameter automatic identification of PMSM

CHEN Zhi-jin，MA Yan
（N0.58 Research Institute of China Ordnance Industries，Mianyang 621000，China）

According tothe characteristics of different parameters of AC servo drive motor difference is only applicable to a specific parameter，a permanent magnet synchronous motor （PMSM）parameter automatic identificationcontrol algorithm which based on Smith predictive compensation and RBF neural network combined with PID controller is introduced in the study.The method uses a Smith predictor to overcome the pure lag and RBF can deal with nonlinear problems，online learning setting PID parameter advantages，is more effective in PMSM parameter automatic identification control system.Finally，the paper establishesthesimulationmodeofthecontrol algorithm，experimental results show that，the algorithm can effectively identify the stator resistance，inductance，and get ideal experimental results.

PMSM；Smith predictive compensation；RBF neural network；PID control

TN-9

A

1674－6236（2016）04-0144-04

2015-07-27 稿件编号：201507174

国家自然科学基金项目（61133016）

陈志锦（1979—），男，云南丽江人，硕士，高级工程师。研究方向：数控技术。