辅助变量纯方位目标跟踪算法

蔚 婧1，文 珺2，李彩彩3，李亚安1

（1.西北工业大学航海学院，陕西西安 710072；2.广西大学计算机与电子信息学院，广西南宁530004；3.西安电子科技大学电子工程学院，陕西西安 710071）

辅助变量纯方位目标跟踪算法

蔚 婧1，文 珺2，李彩彩3，李亚安1

（1.西北工业大学航海学院，陕西西安 710072；2.广西大学计算机与电子信息学院，广西南宁530004；3.西安电子科技大学电子工程学院，陕西西安 710071）

为克服伪线性估计方法在纯方位目标跟踪中估计参数的有偏性，提出了一种改进的辅助变量算法.该算法通过曲线拟合前几个时刻的方位角测量序列来获得当前时刻目标方位角的估计值，并将此作为辅助变量，通过最小二乘方法对目标参数进行估计，理论上可以获得目标参数的无偏估计.针对单、双观测站两种不同情况，推导出了系统观测模型，并给出了具体实现步骤.仿真实验的结果表明，与已有的研究相比，该算法具有更快的收敛速度和更高的估计精度，在工程实践中具有广泛的应用.

目标跟踪；伪线性估计；辅助变量；控制理论

纯方位跟踪（Bearings-Only Tracking，BOT）是一种被动跟踪方式，它只利用获得的目标方位角信息来对目标运动参数进行估计，具有相当好的隐蔽性，近年来已成为我国跟踪预警系统中的重要组成部分［1-2］.量测方程的非线性和目标不完全可观测性是纯方位目标跟踪存在的难点问题［3-5］.

目前应用于纯方位目标跟踪的典型方法主要包括:极大似然估计器（Maximum Likelihood Estimator，MLE）［6-7］，伪线性估计器（Pseudo-Linearing Estimator，PLE）［8-9］，扩展卡尔曼滤波方法（Extended Kalman Filter，EKF）［10］等.其中，伪线性估计器是解决非线性估计的有效方法，它计算量小，便于工程实现，缺点是该方法会产生有偏估计，但由于其在工程上的实用性，仍然受到众多学者的关注.为了消除伪线性估计器方法的有偏性，基于辅助变量的伪线性估计器算法被提出，它可以获得理论上的无偏估计，其中核心问题是辅助变量的选择.

在研究现有算法的基础上，笔者提出一种改进的辅助变量构造方法.该方法通过曲线拟合前几个时刻的方位角测量序列来获得当前时刻目标方位角的估计值，并将此作为辅助变量，通过最小二乘方法估计目标参数，理论上可以获得目标参数的无偏估计.

1 纯方位目标跟踪系统模型

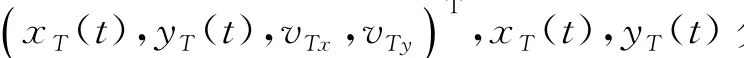
分别为目标在t时刻位于X，Y轴方向上的坐标分量，vTx，vTy表示目标在X，Y轴方向上的速度分量.观测站1位于坐标原点，观测站2位于X轴上，观测站间距为d，目标距坐标原点的初始距离为D0.

β1（k），β2（k）分别为观测站1和观测站2观测到的方位角序列，以Y轴顺时针旋转0～2π:

由于存在“距离模糊”［4］的问题，仅依靠静止单观测站所获得的目标方位信息，无法同时解算出目标的距离、航向、速度等全部参数.为了获得目标的所有运动参数，必须使用两个以上的观测站，或者使观测站机动.虽然单观测站不能获得目标的所有参数，但是却可以获得目标速度与初始距离的比值，在这种情况下，若对目标速度具有一定先验知识，同样可通过先验知识对目标参数进行解算，实现完全观测.为此，以下分别对单、双观测站的辅助变量伪线性估计算法进行分析.

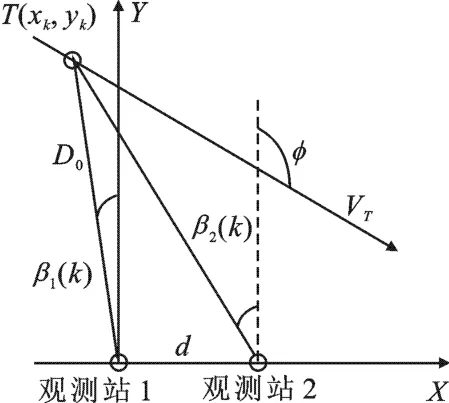
图1　双观测站纯方位目标跟踪几何关系示意图

2 单观测站辅助变量伪线性估计算法

以图1中位于坐标原点的观测站为例进行分析.在任意时刻j，有

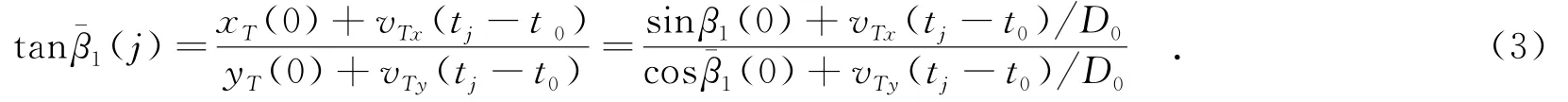
将式（2）代入式（3），可得

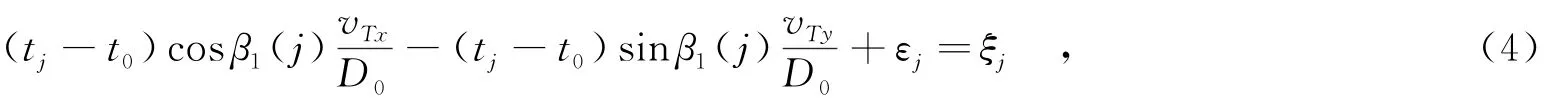
其中，ξj=sin（β1（j）-β1（0））；εj为等效的测量误差.

定义目标状态矢量X0=［vTxD0，vTyD0］T，并将式（4）改写成矩阵形式，可得伪测量方程为

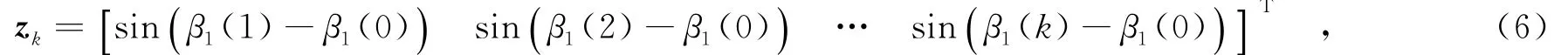
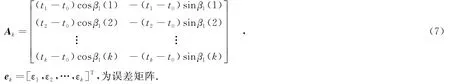
其中，可得式（5）的最小二乘解为

对式（8）取数学期望，得

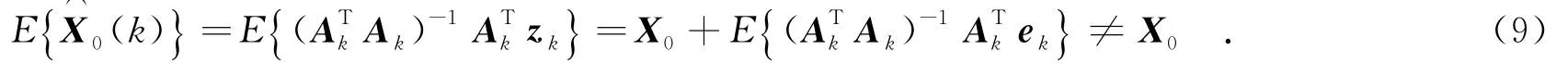
可知式（8）为有偏估计，为此引入辅助变量来消除有偏估计.可选取上式的最优辅助变量估计，为

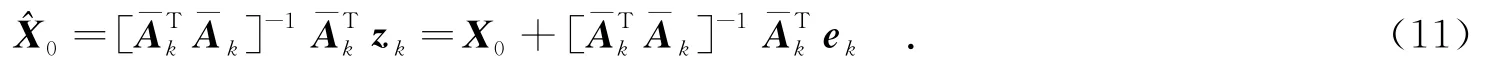
采用最小二乘曲线拟合算法，利用前3个时刻测量的方位角β1（j-3），β1（j-2），β1（j-1），进行n次曲线拟合.由于拟合的精度并不正比于拟合曲线的次数，并且考虑到每次观测的时间间隔较短，因此在实际应用中选取二次曲线拟合.

设β1（j-3），β1（j-2），β1（j-1）确定了如下的二次曲线:

其中，a0，a1，a2为多项式系数.

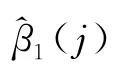
3 双观测站辅助变量伪线性估计算法

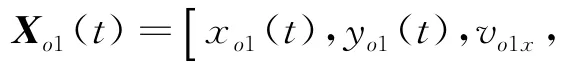
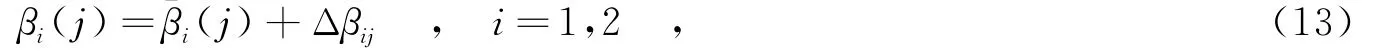
同理，可以得到

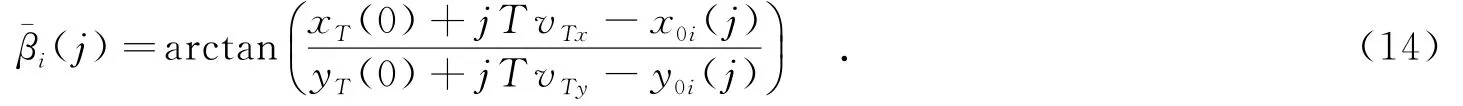
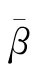
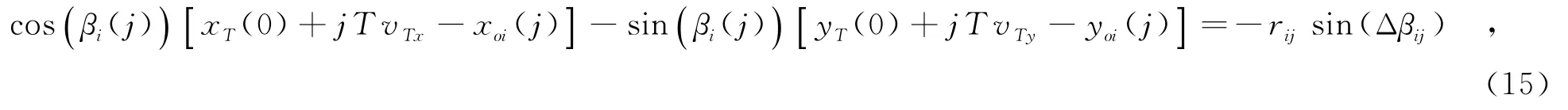
其中，rij表示在j时刻目标与观测站i的径向距离.由式（15）得到伪线性测量方程为

其中，

同理，可得基于辅助变量的最小二乘估计为

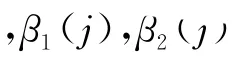
4 计算机仿真与分析

为验证上述方法的有效性，进行了计算机仿真实验，具体参数如下:目标速度V=10 m/s，目标航向ϕ=140°，目标与坐标原点的初始距离D0=40 km，初始方位角β1（0）=30°，采样周期T=1 s.每条曲线均经过40次蒙特卡罗实验获得.

4.1单观测站情况

观测站静止于坐标（0，0）处，观测噪声的均方差Δβ1=2°.由于静止单站对目标的观测属于不完全观测，因此只能获得目标速度与初始距离的比值.为了对估计结果进行定量分析，引入均方误差进行比较.

图2比较了用笔者提出的方法和文献［8］中的方法构造辅助变量获得目标参数估计值的均方误差曲线.从图2（a）和图2（b）对目标速度与初始距离的比值估计可以看出，笔者提出的方法只需十几次采样就可获得参数的稳定估计，而文献［8］中的方法则需要50次左右的采样才可以达到稳定估计，而且均方误差也较文献［8］中的方法有所降低.图2（c）为目标航向角均方误差曲线，可以看出笔者提出的方法无论是收敛速度还是估计精度均优于文献［8］中方法的.

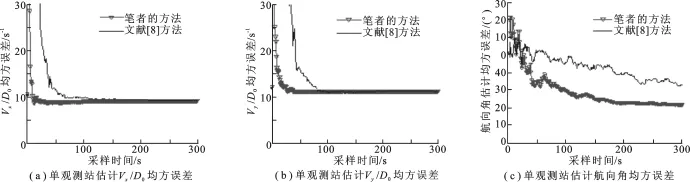
图2　单观测站估计均方误差

4.2双观测站情况

观测站分别静止于（0，0）和（500，0）处，观测噪声的均方差Δβ1=Δβ2=2°.由于双观测站可以实现对目标的完全观测，图3分别给出了两种方法对目标参数估计的对比.

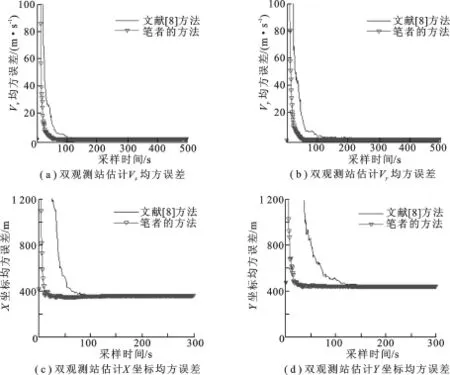
图3　双观测站估计均方误差

从仿真结果可以看出，与单观测站情况类似，笔者提出的方法获得的目标参数估计值均能快速收敛到稳定值，而且具有较低的估计误差，便于在工程应用中快速对目标进行定位.

5 总 结

笔者结合纯方位观测的系统模型，提出了一种改进的基于辅助变量的纯方位目标跟踪方法.该方法通过曲线拟合前几个时刻的方位角测量序列获得当前时刻目标方位角的估计，并作为辅助变量，得到目标参数的最小二乘估计，可获得理论上的无偏估计.笔者针对单、双观测站的不同情况，对算法的具体实现步骤进行了推导.仿真实验表明，笔者提出的方法相较于文献［8］中的方法具有更快的收敛速度和更小的估计误差，便于快速实现对目标的准确定位，在工程实践中具有重要的应用价值.

［1］NORTHARDT E T，BILIK I，ABRAMOVICH Y.Bearings-only Constant Velocity Target Maneuver Detection via Expected Likelihood［J］.IEEE Transactions on Aerospace and Electronic Systems，2014，50（4）:2974-2988.

［2］周红波，万福，蔡祥.基于改进Rao-Blackwellized粒子滤波的WSN被动目标跟踪［J］.火力与指挥控制，2015，40 （6）:44-47. ZHOU Hongbo，WAN Fu，CAI Xiang.Passive Target Tracking Using Modified Rao-blackwellized Particle Filter［J］. Fire Control&Command Control，2015，40（6）:44-47.

［3］胡子军，张林让，赵珊珊，等.组网无源雷达高速多目标初始化及跟踪算法［J］.西安电子科技大学学报，2014，41 （6）:25-30. HU Zijun，ZHANG Linrang，ZHAO Shanshan，et al.Joint Initialization of High-speed Targets via Multistatic Passiveradar Measurements and Its Tracking Algorithm［J］.Journal of Xidian University，2014，41（6）:25-30.

［4］许志刚，盛安冬.二维单站纯方位运动目标跟踪的可观测性［J］.兵工学报，2007，28（5）:617-620. XU Zhigang，SHENG Andong.Observability for Two-dimensional Single Observer Tracking Based on Bearing-onlyMeasurements［J］.Acta Armamentarii，2007，28（5）:617-620.

［5］时银水，姬红兵，杨柏胜.组网无源雷达变数目多目标跟踪算法［J］.西安电子科技大学学报，2010，37（2）:218-223. SHI Yinshui，JI Hongbing，YANG Baisheng.Multiple Passive-radar Based Time-varying Number Targets Tracking ［J］.Journal of Xidian University，2010，37（2）:218-223.

［6］FONG L W.Multi-sensor Track-to-track Fusion Using Simplified Maximum Likelihood Estimator for Maneuvering Target Tracking［C］//2007 IEEE International Symposium on Industrial Electronics.Piscataway:IEEE，2007:36-41.

［7］NIU R X，BLUM R S，VARSHNEY P K，et al.Target Localization and Tracking In Noncoherent Multiple-input Multiple-output Radar Systems［J］.IEEE Transactions on Aerospace and Electronic Systems，2012，48（2）:1466-1489.

［8］石章松，刘忠，王树宗.一种单站纯方位目标跟踪算法研究［J］.系统工程与电子技术，2005，27（2）:349-352. SHI Zhangsong，LIU Zhong，WANG Shuzong.Study of the Single Platform Bearing-only Target Tracking Algorithm ［J］.Systems Engineering and Electronics，2005，27（2）:349-352.

［9］CHAN Y T，RUDINCK S W.Bearings-only and Doppler-bearing Tracking Using Instrumental Variables［J］.IEEE Transactions on Aerospace and Electronic Systems，1992，28（4）:1076-1083.

［10］CHEN J G，WANG N，MA L L，et al.Extended Target Probability Hypothesis Density Filter Based on Cubature Kalman Filter［J］.IET Radar，Sonar&Navigation，2015，9（3）:324-332.

（编辑:郭 华）

Modified instrumental variable method for bearings-only target tracking

YU Jing1，WEN Jun2，LI Caicai3，LI Ya’an
（1.College of Marine Science and Technology，Northwestern Polytechnical Univ.，Xi’an 710072，China；2.School of Computer&Electrical Information，Guangxi Univ.，Nanning 530004，China；3.School of Electronic Engineering，Xidian Univ.，Xi’an 710071，China）

To overcome the biased estimation of the pseudo-linear algorithm in bearings-only target tracking，a modified instrumental variable algorithm is proposed.In the new algorithm，the current bearings-only estimation angle is acquired by polyfitting several previous bearings angles.Then the estimated angle is used as the instrumental variable to get the motion parameters by applying the leastsquare method.The algorithm can achieve the theoretical unbiased estimation.Simulation results illustrate that the new modified instrumental variable algorithm has a better convergence rate and estimation accuracy than the existing research and that it is more suitable for engineering practice.

target tracking；pseudo-linear estimation；instrumental variable；control theory

TN953

A

1001-2400（2016）01-0167-06

10.3969/j.issn.1001-2400.2016.01.030

2015-05-06

国家自然科学基金资助项目（51409214，51179157，61461007）

蔚 婧（1982-），女，讲师，E-mail:yujing@nwpu.edu.cn.