风屏障透风率对侧风下大跨度斜拉桥车-桥耦合振动的影响

何玮，郭向荣，，邹云峰，，何旭辉，，杨著

（1. 中南大学 土木工程学院，湖南 长沙，410075；2. 中南大学 高速铁路建造技术国家工程实验室，湖南 长沙，410075）

风屏障透风率对侧风下大跨度斜拉桥车-桥耦合振动的影响

何玮1，郭向荣1，2，邹云峰1，2，何旭辉1，2，杨著1

（1. 中南大学 土木工程学院，湖南 长沙，410075；2. 中南大学 高速铁路建造技术国家工程实验室，湖南 长沙，410075）

为研究风屏障透风率对侧风下大跨度斜拉桥车桥系统耦合振动的影响，通过风洞试验得出在桥梁上设置不同透风率风屏障情况下桥梁和桥上不同位置处列车的三分力系数，在此基础上根据弹性系统动力学总势能不变值原理进一步建立考虑风荷载的车桥系统耦合振动方程对侧风作用下大跨度斜拉桥车桥动力响应进行计算。研究结果表明：当风屏障透风率由 10%增大至 40%，迎风和背风工况下跨中处桥面竖向位移最大值均呈现增大趋势；风屏障透风率对迎风工况车辆动力响应的影响较大；当风屏障透风率由 30%增大至 40%时，车辆的脱轨系数、轮重减载率和横向摇摆力增幅较为明显。

风屏障；斜拉桥；耦合振动；动力响应

在大跨度桥梁上设置风屏障的主要目的在于提高桥梁上列车在侧风作用下的行车安全。对设有普通型风屏障的桥梁，如果侧向来流的风速很大，风屏障虽然可以为列车提供一个风速相对较低的行车环境，但它对整个桥梁结构带来了较大的气动作用力，可能超过强度设计规定的风荷载，引起桥梁动力稳定性下降［1］。因此研究风屏障透风率对侧风下大跨度斜拉桥车桥系统耦合振动的影响是十分必要的。国内外学者们以往的研究主要集中在风屏障对列车所受气动力的影响，而风屏障对车桥耦合振动影响的研究并不多：種本勝二等［2-3］通过系列化风洞模型试验研究了风屏障透风率以及高度对侧风作用下列车所受气动力的影响；向活跃［4］通过风洞试验和数值模拟2种方法较为系统地分析了风屏障对桥梁和列车气动性能的影响；李田等［5］通过数值模拟的方法研究了高速列车通过风屏障时的车辆响应。本文作者在以往研究的基础上，先通过风洞试验获得在桥梁上设置不同透风率风屏障情况下桥梁和桥上不同位置处列车的三分力系数，再将三分力系数与脉动风谱生成的脉动风荷载作为外部激励，轨道不平顺作为系统的自激激励源，建立考虑风荷载作用的车桥系统耦合振动方程，对风屏障透风率的变化对侧风下大跨度斜拉桥车桥系统耦合振动的影响进行研究。

1 风洞试验研究

1.1 试验模型

风洞试验在中南大学风洞实验室高速实验段进行，高速段长×宽×高为15 m×3 m×3 m，顺风向湍流度为0.5%。来流风速为10 m/s，风向角为90°，风攻角为-3°，0°和+3°。利用4个测力天平同步测试列车及桥梁所受气动荷载。桥梁模型为钢骨架木质模型，车辆模型为钢骨架塑料模型，模型缩尺比为1/40。桥梁与列车模型长度为2 m，为减少端部绕流的影响，在模型两端加装端板。列车与桥梁模型尺寸如图1所示，桥梁模型采用某大跨度斜拉桥钢箱梁段主梁外形，桥面加装2条宽度为70 mm轨道板，风屏障距桥梁中心处距离为184 mm。列车模型采用地铁A型车，列车模型高度为110 mm、宽度为89 mm，具体尺寸参照GB 50157—2003“地铁设计规范”［6］确定。

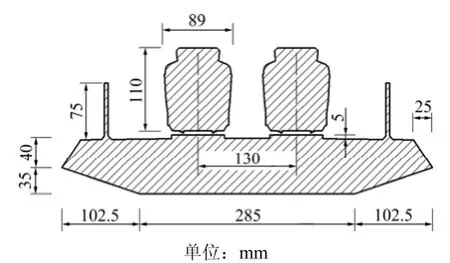
图1 车-桥系统模型尺寸Fig.1 Geometric model of train-bridge system

1.2 风洞试验结果

为研究风屏障透风率对侧风下列车和桥梁三分力系数的影响，在主梁模型两侧上分别加装10%，20%，30%和40%透风率的风屏障，风屏障的开孔方式统一为8 mm×8 mm矩形孔洞，并在风屏障上均匀分布。根据以往的研究［7-12］，桥梁上风屏障高度宜设置在2～4 m之间，本文的风屏障高度为3 m，按缩尺比1/40换算后的风屏障高度为75 mm。风洞试验共测试在4种透风率风屏障下，列车分别处于桥梁迎风侧和背风侧共计8种工况。在考虑了列车与桥梁间气动力相互影响的前提下，通过4个六分量天平测出的数据经过整理得出风攻角为 0°下列车及桥梁的三分力系数见表1。

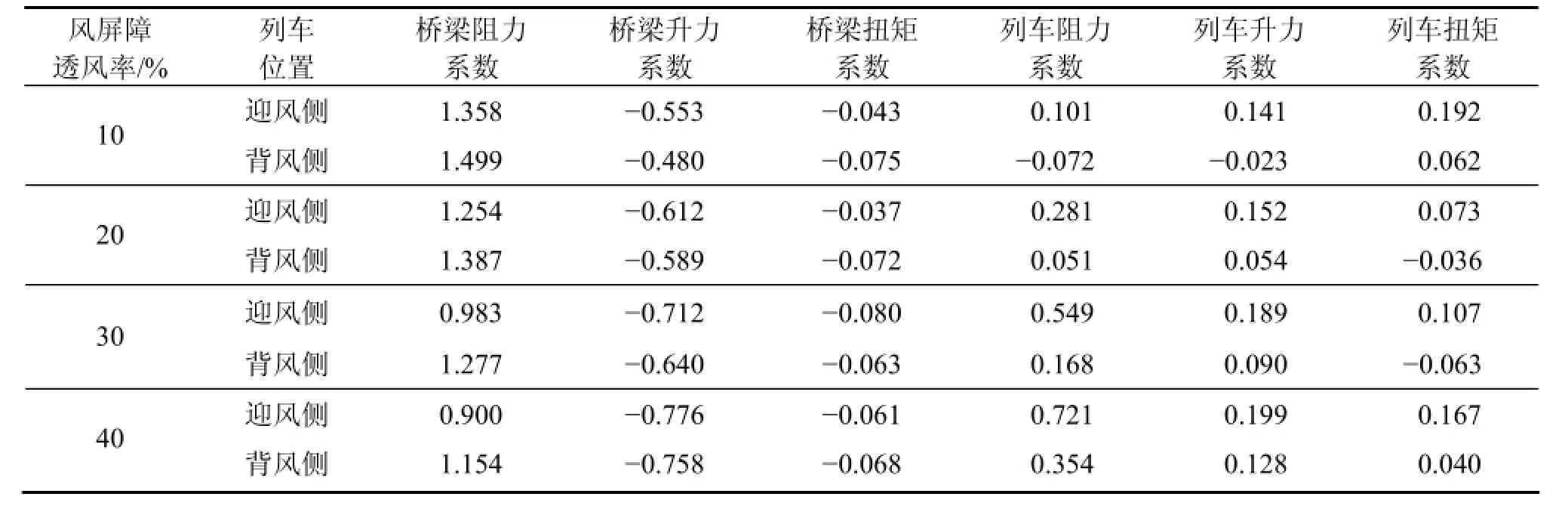
表1 三分力系数Table 1 Aerodynamic coefficients

2 风-车-桥系统动力学计算模型的建立

本文在建立风荷载作用下车桥耦合振动方程时，根据弹性系统动力学总势能不变值原理［13］及形成矩阵的“对号入座”法则［14］，将桥上列车与桥梁视为 1个整体系统，轨道不平顺作为系统的自激激励源，风荷载作为外部激励，建立考虑风荷载作用的车桥耦合系统振动方程。风-车-桥耦合系统的非线性振动方程为

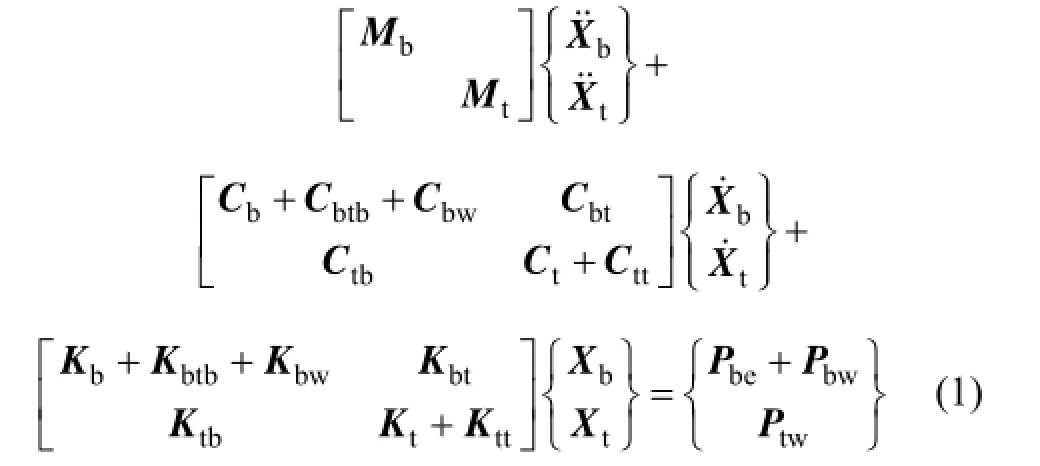
其中：Mb和Mt分别为桥梁和列车的质量矩阵；Cb和Ct分别为桥梁和列车的阻尼矩阵；Cbtb和Ctb为车桥耦合系统中由桥梁振动速度引起的阻尼矩阵；Cbt和 Ctt为车桥耦合系统中由列车振动速度引起的阻尼矩阵；Cbw为由脉动风力所产生的阻尼矩阵；Pbe为作用在桥梁结构上的列车自重荷载；Pbw和Ptw分别为作用在桥梁和列车上的风荷载；Xb和Xt分别为桥梁和列车的位移；K为列车及桥梁的刚度矩阵，其下标的意义和阻尼矩阵一致。

在数值算法上，本文应用Wilson-θ逐步积分法直接求解风荷载作用下车桥耦合系统振动方程。

2.1 脉动风场

对于风-车-桥系统动力学计算模型而言，脉动风场可近似看作沿桥梁顺桥向若干点处随机风波的合成［15］，随机风场可视为一维多变量的平稳高斯随机过程，按Shinozuka理论计算其互谱密度矩阵，并通过对脉动风速谱密度矩阵显式分解和FFT技术的运用，高效率地模拟随机过程的样本［16］。

该方法基本原理为：对于一个零均值的一维n变量高斯过程｛f（t）｝，它包含f1（t），f2（t），…，fn（t）等n个变量，其互谱密度矩阵为S0（ω），参照Shinozuka的相关理论，随机过程｛f（t）｝的样本可以由下式来模拟：

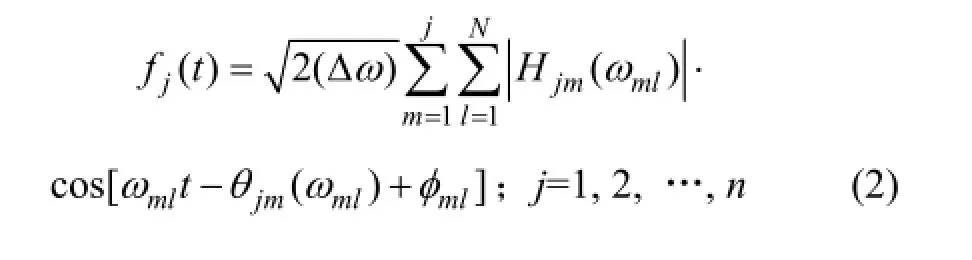
其中：N为足够大的正整数；Δω为计算频率的增量；φml为分布在［0， 2π］之间的随机变量；ωml为双索引频率；Hjm（ωml）为矩阵H（ω）中的元素。

本文在模拟风荷载时，考虑了桥址各点之间的空间相关性，在沿线路方向上共模拟了29个风速点，风速点的水平间距为20 m，两风速模拟点之间的脉动风速时程曲线利用其相邻的2个模拟点进行线性内插求得。风速时程的计算时间步长取0.1 s，样本长度为50 s。图2给出了平均风速为25 m/s时第15点（主跨跨中附近）的脉动风速时程曲线。

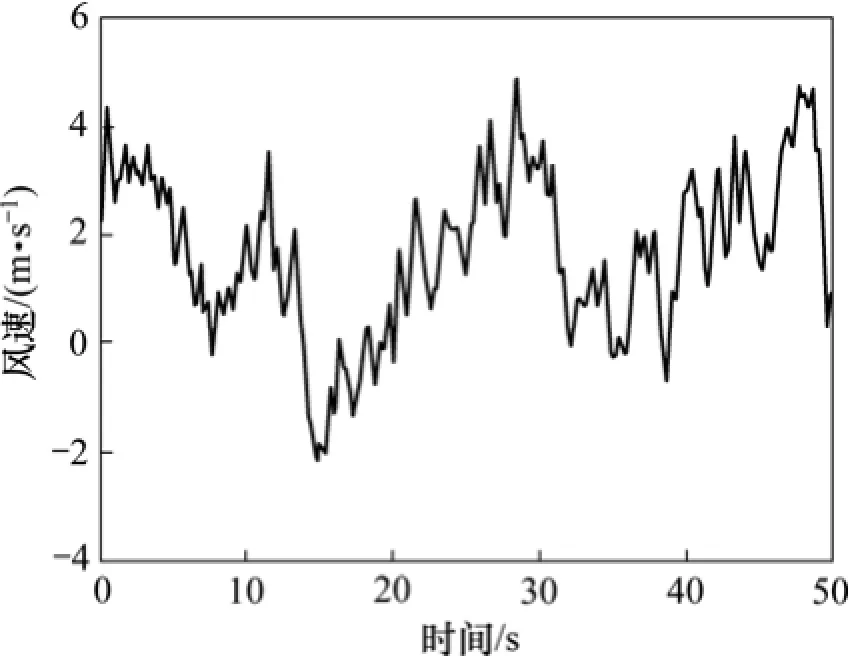
图2 沿主梁方向第15点的脉动风速时程曲线Fig.2 Simulated wind speed curve of the 15th point of bridge deck

2.2 列车计算模型

列车计算模型由车体、构架及轮对共7个刚体以及一、二系悬挂组成，本文进行耦合振动分析时采用以下假定：1） 车体、构架和轮对均为刚体；2） 不考虑列车纵向自由度；3） 不考虑轮对的侧滚、点头的自由度；4） 弹簧、蠕滑力为线性关系，阻尼为粘滞阻尼；5） 轮对与桥上轨道在铅垂方向位移保持一致。这样车体及前后构架在空间上有侧摆、侧滚、点头、摇头以及浮沉等5个自由度，每个轮对则有侧摆、摇头2个自由度，可知四轴机车车辆为23个自由度［17］。

2.3 桥梁计算模型

本文桥梁计算模型采用（51+69+340+69+47） m某双塔双索面混合梁斜拉桥，边跨设置辅助墩，大桥中心线为直线，全桥长583.22 m，中跨主梁采用正交异性桥面板流线型扁平钢箱梁，两行车线间距为5.4 m，斜拉索采用双索面平形布置，每塔共13对斜拉索。

本文中桥梁采用空间梁-索系有限元分析模型。对空间梁单元模型，采用二节点空间直梁单元，考虑其竖向、横向受弯以及扭转变形，每个节点考虑3个线位移与3个转角位移，整个单元有12个自由度；对空间索单元模型，单元节点数为2，节点自由度数为3。墩底处地基基础的刚度分别叠加于相应的节点上。桥梁系统的阻尼按Rayleigh阻尼考虑，材料弹性模量和泊松比按现行桥规取值，二期恒载作为均布质量分配到相应的桥梁单元中。由此建立斜拉桥有限单元模型如图3所示。

图3 桥梁有限元模型Fig.3 Finite element model of bridge

3 风屏障透风率对风-车-桥系统耦合振动的影响分析

3.1 计算工况

本文采用美国六级谱模拟轨道不平顺，列车编组为动+拖+动+动+拖+动6辆编组。列车采用地铁A型车，列车轴重为170 kN，车速为80 km/h，桥面风速为25 m/s。加装不同透风率风屏障的桥梁与列车的三分力系数按表1取值，本文计算了桥梁风屏障透风率分别为10%，20%，30%和40%时，在侧风作用下列车分别处于桥梁迎风侧和背风侧行车共计8种工况的车桥动力响应。

3.2 计算结果及分析

为了研究列车在桥面行车位置对桥梁横向位移动力响应的影响，图4给出了无风情况下迎风与背风行车时桥梁跨中横向位移时程曲线。从图4可以看出：迎风与背风行车时，在行车线相对于桥面中轴线偏心荷载的作用下，跨中处桥面产生横向位移的方向是相反的。

在侧风作用下，列车行驶通过加装不同透风率风屏障的斜拉桥时，自上桥至下桥时域内桥梁的动力响应最大值见表2，从表2可以看出：当风屏障透风率由10%增大至40%时，桥梁跨中处桥面横向与竖向位移最大值变化较明显，而横竖向加速度最大值无变化；随着风屏障透风率增大，列车处于迎风侧与背风侧时跨中处桥面竖向位移最大值均呈现增大趋势，而横向位移最大值的变化趋势则较为复杂。因此为了进一步显示跨中处桥面位移的变化情况，图5和图6所示分别为桥梁跨中处桥面横向和竖向位移的时程曲线。

从图5可以看出：随着风屏障透风率增大，桥面横向初始位移基本保持减小趋势，这是由于此时影响桥面横向位移的外部荷载只有风荷载。当时间t=12.5 s时，列车头车恰好到达桥梁跨中处，此时桥梁横向位移开始出现较大波动，但迎风工况和背风工况的波动趋势有明显差异，其原因在于当列车行驶至桥梁跨中处时，跨中处桥面不仅受风荷载作用还受行车线相对于桥面中轴线偏心荷载的作用，迎风工况下该偏心荷载使桥面产生与侧向风反向的横向位移，而背风工况下该偏心荷载使桥面产生与侧向风同向的横向位移。随着风屏障透风率增大，列车所受风荷载显著增大，其对桥梁横向位移的影响表现在当列车行驶至桥梁跨中处，桥梁横向位移的波动幅度明显增大。

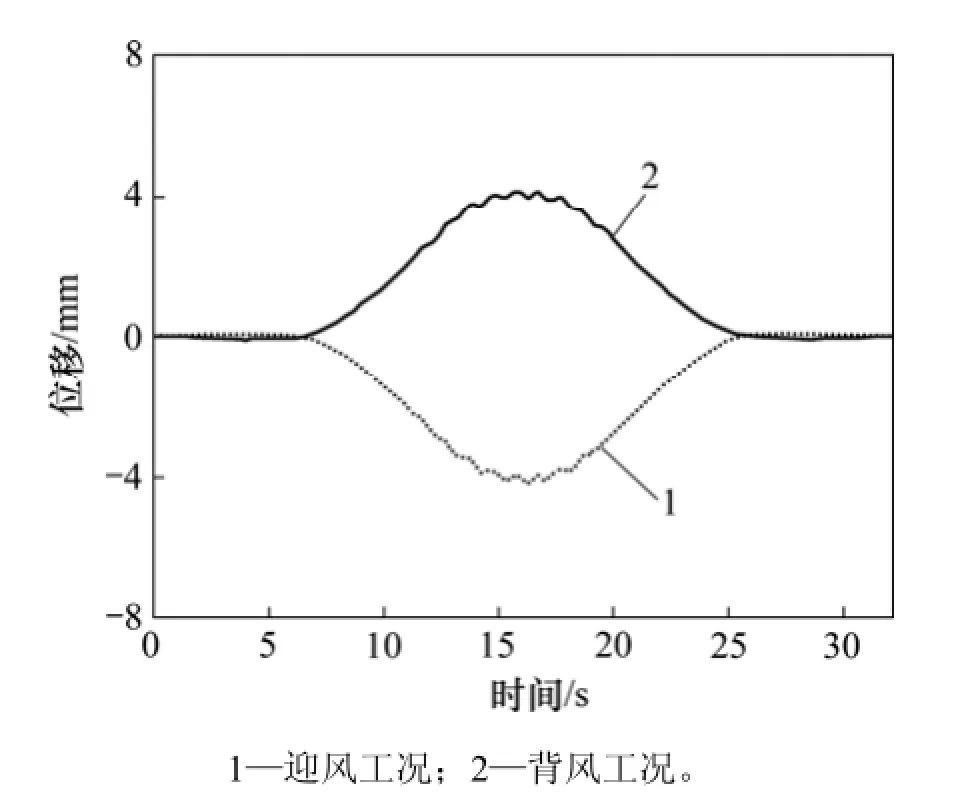
图4 无风情况下桥梁跨中横向位移时程曲线Fig.4 Lateral displacement curves of bridge deck at middle span when U is 0 m/s

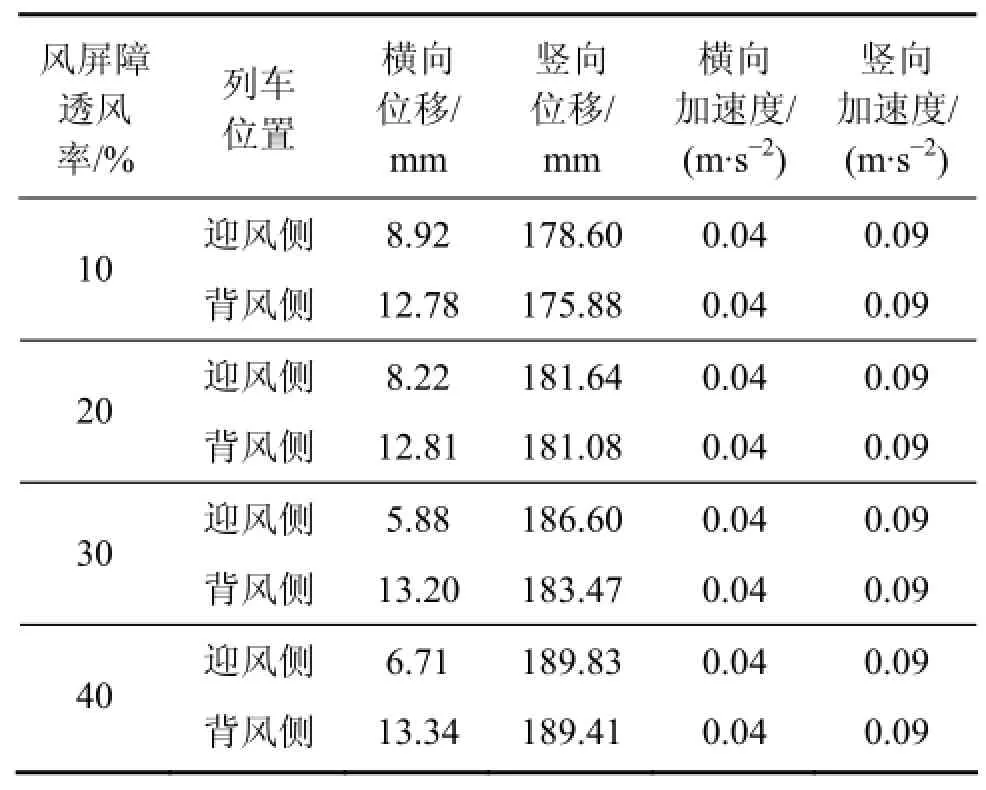
表2 风屏障不同透风率下桥梁响应最大值Table 2 Maximum responses of bridge with different pored wind barriers

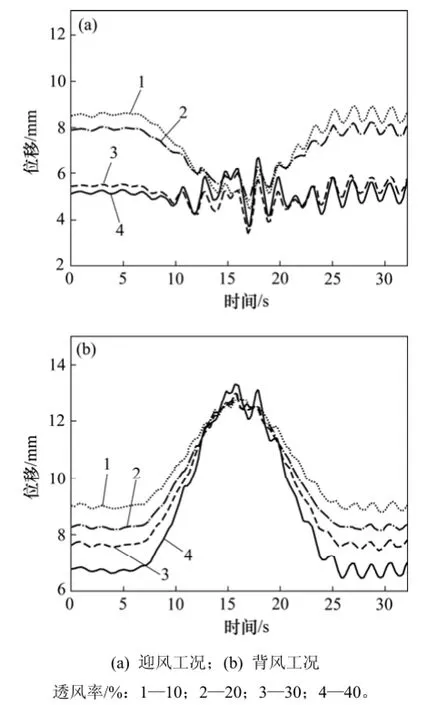
图5 风速U=25 m/s情况下桥梁跨中横向位移时程曲线Fig.5 Lateral displacement curves of bridge deck at middle span when U is 25 m/s

从图6可以看出：迎风行车与背风行车时，跨中桥面竖向位移变化基本保持一致；与横向位移时程曲线相比，并未出现明显上下波动，这是由于行车线荷载对桥梁竖向位移的影响远大于脉动风荷载的作用，且桥梁在侧向风作用下受到的阻力也远大于升力。

在侧风作用下，列车行驶通过加装不同透风率风屏障的斜拉桥时，车辆的动力响应最大值见表 3。从表3可以看出：风屏障透风率的变化对迎风工况下车辆动力响应的影响较大，这是由于列车处于桥梁迎风侧时所受风荷载较大；随着风屏障透风率增大，列车脱轨系数、轮重减载率和横向摇摆力均呈现增大趋势；当风屏障透风率由10%增大至20%时，车辆的动力响应最大值变化不明显，从脱轨系数上看均为0.10，而随着透风率进一步增大，车辆的动力响应最大值的增幅更加明显。

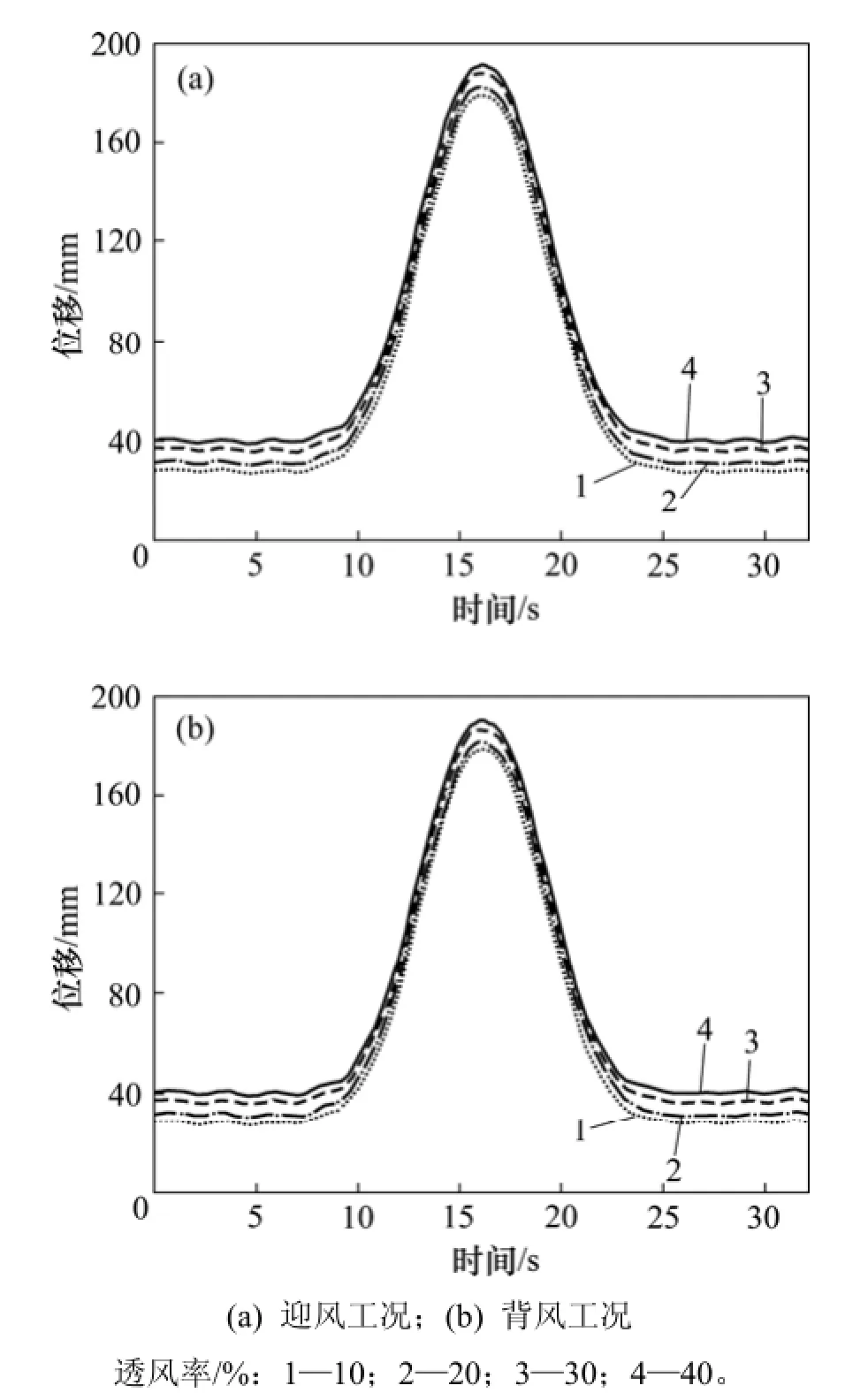
图6 风速U=25 m/s情况下桥梁跨中竖向位移时程曲线Fig.6 Vertical displacement curves of bridge deck at middle span when U is 25 m/s

为了更好地显示设置了不同透风率风屏障情况下车辆响应随时间的变化趋势，图7给出了第1辆列车第1轮对相对于轨面的位移时程曲线。从图7可以看出：风屏障透风率的变化对迎风工况下列车头车第 1轮对相对横向位移时程的影响较为明显；而列车行驶至跨中处时，迎风工况下头车第一轮对相对横向位移比背风工况小，这是由于列车处于迎风侧时，当列车行驶至桥梁跨中处，行车线相对于桥面中轴线的偏心荷载使桥面产生与侧向风反向的横向位移，该位移与列车所受侧向风荷载产生的位移相抵消，因此，迎风工况列车轮对相对横向位移比背风工况的小。

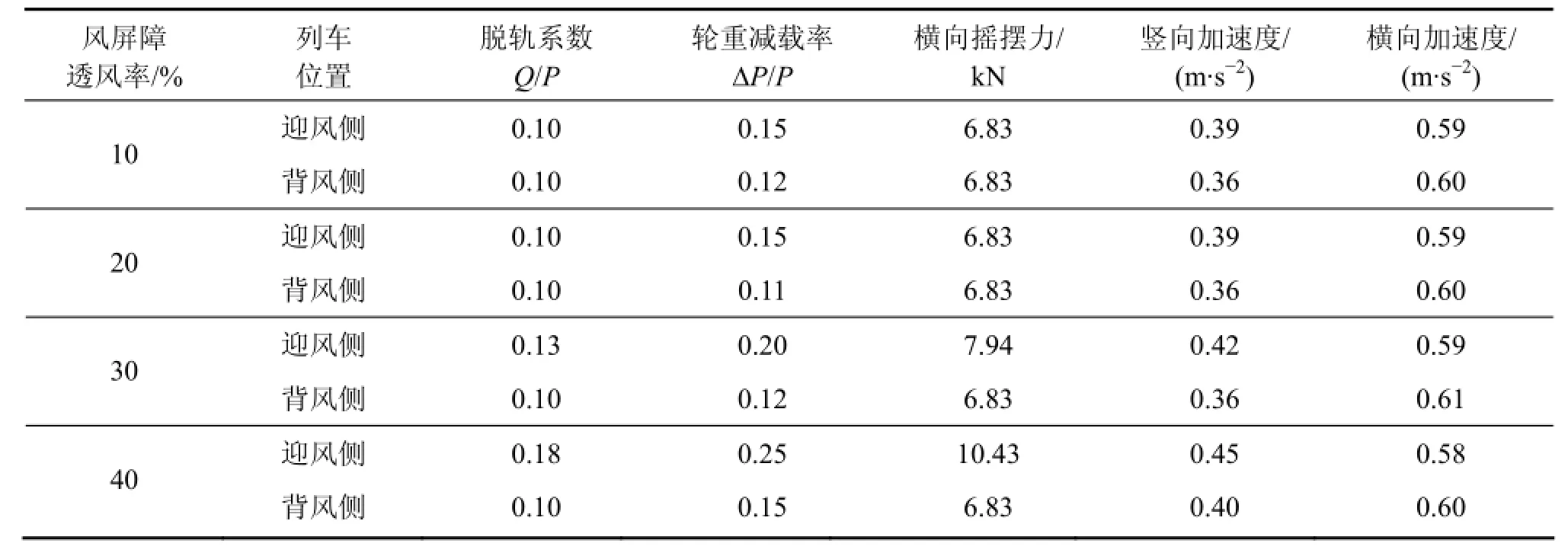
表3 风屏障不同透风率下车辆响应最大值Table 3 Maximum responses of trains with different pored wind barriers

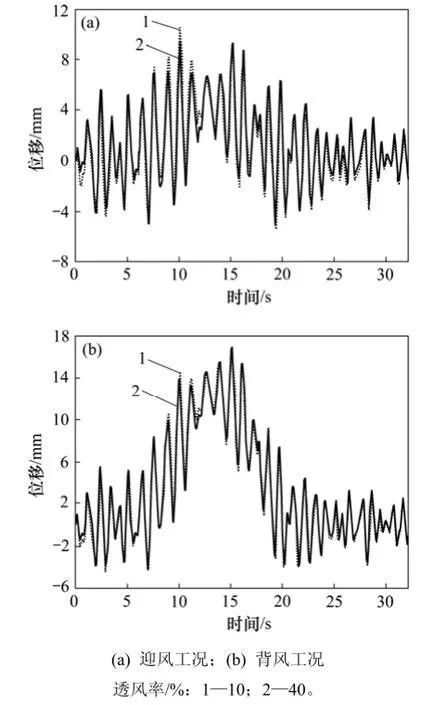
图7 第一辆列车第一轮对相对于轨面位移时程曲线Fig.7 Lateral displacement curves of the first wheel pair relative to rail surface

4 结论

1） 在桥梁上设置不同透风率风屏障时，列车和桥梁的三分力系数风洞试验结果变化均比较明显，因此有必要对设置不同透风率风屏障的桥梁进行风-车-桥耦合振动分析。

2） 当风屏障透风率由10%增大至40%时，桥梁跨中处桥面横向与竖向位移最大值变化较明显，而横竖向加速度最大值无变化；随着风屏障透风率增大，列车处于迎风侧与背风侧时跨中处桥面竖向位移最大值均呈现增大趋势，而横向位移最大值的变化趋势则较为复杂。

3） 随着风屏障透风率增大，跨中桥面横向初始位移基本保持减小趋势，这是由于此时影响桥面横向位移的外部荷载只有风荷载；当列车到达桥梁跨中处，跨中桥面横向位移开始出现较大波动，但迎风工况和背风工况的波动趋势有明显差异，这是由于当列车行驶至桥梁跨中处时，跨中处桥面不仅受风荷载作用还受列车行车线相对于桥面中轴线偏心荷载的作用。

4） 风屏障透风率的变化对迎风工况下车辆动力响应的影响较大，这是由于列车处于桥梁迎风侧时所受风荷载较大。

5） 当风屏障透风率由10%增大至20%时，车辆的脱轨系数、轮重减载率和横向摇摆力基本无变化，而当风屏障透风率由30%增大至40%，车辆的脱轨系数、轮重减载率和横向摇摆力增幅较为明显。

［1］ OSTENFELD K H. Bridge engineering and aerodynamics［C］// BALKEMA A A. Proceeding of the First International Symposium on Aerodynamics of Large Bridges. Copenhagen，1992： 3-22.

［2］ 種本勝二， 铃木実， 前田逹夫， 等. 横風に對する車輛の空氣力學的特性風洞試驗［R］. 東京都： 鉄道総合技術研究所，1999： 47-52. TANEMOTO S， SUZUKI M， MAEDA T， et al. Wind-tunnel test investigations and analysis on aerodynamic performance of train in crosswind［R］. Tokyo： Railway Technical Research Institute，1999： 47-52.

［3］ 種本勝二， 铃木実， 斎藤寛之， 等. 强風下での車輛に动く空氣力と低减對策に關する風洞試驗［R］. 東京都： 鉄道総合技術研究所， 2004： 17-22. TANEMOTO S， SUZUKI M， SAITOH H， et al. Wind-tunnel test investigations and analysis on measures to minimize aerodynamic force of train in strong wind［R］. Tokyo： Railway Technical Research Institute， 2004： 17-22.

［4］ 向活跃. 高速铁路风屏障防风效果及其自身风荷载研究［D］.成都： 西南交通大学土木工程学院， 2013： 22-89. XIANG Huoyue. Protection effect of wind barrier on high speed railway and its wind loads［D］. Chengdu： Southwest Jiaotong University. School of Civil Engineering， 2013： 22-89.

［5］ 李田， 张继业， 张卫华. 横风下高速列车通过挡风墙动力学性能［J］. 铁道学报， 2012， 34（7）： 31-35. LI Tian， ZHANG Jiye， ZHANG Weihua. Dynamic performance of high-speed train passing windbreak in crosswind［J］. Journal of the Chinese Railway Society， 2012， 34（7）： 31-35.

［6］ GB 50157—2003， 地铁设计规范［S］. GB 50157—2003， Code for design of metro［S］.

［7］ 张健. 铁路防风栅抗风性能风洞试验研究与分析［J］. 铁道科学与工程学报， 2007， 4（1）： 13-17. ZHANG Jian. Wind-tunnel test investigations and analysis on wind break performances of wind fences on railway［J］. Journal of Railway Science and Engineering， 2007， 4（1）： 13-17.

［8］ 王厚雄， 高注， 王蜀东， 等. 挡风墙高度的研究［J］. 中国铁道科学， 1990， 11（1）： 14-22. WANG Houxiong， GAO Zhu， WANG Shudong， et al. A study on height of wind break wall［J］. China Railway Science， 1990，11（1）： 14-22.

［9］ 李永乐， 廖海黎， 强士中. 车桥系统气动特性的节段模型风洞试验研究［J］. 铁道学报， 2004， 26（3）： 71-74. LI Yongle， LIAO Haili， QIANG Shizhong. Study on aerodynamic characteristics of the vehicle-bridge system by the section model wind tunnel test［J］. Journal of the China Railway Society， 2004， 26（3）： 71-74.

［10］ 姜翠香， 梁习锋. 挡风墙高度和设置位置对车辆气动性能的影响［J］. 中国铁道科学， 2006， 27（2）： 66-70. JIANG Cuixiang， LIANG Xifeng， Effect of the vehicle aerodynamic performance caused by the height and position of wind-break wall［J］. China Railway Science， 2006， 27（2）： 66-70.

［11］ 何旭辉， 邹云峰， 杜风宇. 风屏障对高架桥上列车气动特性影响机理分析［J］. 振动与冲击， 2015， 34（3）： 66-71. HE Xuhui， ZOU Yunfeng， DU Fengyu. Mechanism analysis of wind barrier’s effects on aerodynamic characteristics of a train on viaduct［J］. Journal of Vibration and Shock， 2015， 34（3）：66-71.

［12］ HE X H， ZOU Y F， WANG H F， et al. Aerodynamic characteristics of a trailing rail vehicles on viaduct based on still wind tunnel experiments［J］. Journal of Wind Engineering and Industrial Aerodynamics， 2014， 135： 22-33.

［13］ 曾庆元， 郭向荣. 列车桥梁时变系统振动分析理论与应用［M］. 北京： 中国铁道出版社， 1999： 35-150. ZENG Qingyuan， GUO Xiangrong. Theory and application of train-bridge time-variant system vibration analysis［M］. Beijing：China Railway Press， 1999： 35-150.

［14］ 曾庆元， 杨平. 形成矩阵的“对号入座”法则与桁段有限元法［J］. 铁道学报， 1986， 8（2）： 48-59. ZENG Qingyuan， YANG Ping. The “set-in-right- position” rule for formulating dynamic system matrix and the finite element method of truss section for spatial analysis of truss girder［J］. Journal of the Chinese Railway Society， 1986， 8（2）： 48-59.

［15］ 曹映泓， 项海帆， 周颖. 大跨度桥梁脉动风场的随机模拟［J］.土木工程学报， 1998， 31（3）： 72-78. CAO Yinghong， XIANG Haifan， ZHOU Yin. Stochastic simulation of wind turbulence field for a long-span bridge［J］. China Civil Engineering Journal， 1998， 31（3）： 72-78.

［16］ YANG W W， CHANG T Y P， CHANG C C. An efficient wind field simulation technique for Bridges［J］. Journal of Wind Engineering and Industrial Aerodynamics， 1997， 67（97）：697-708.

［17］ 郭向荣， 曾庆元. 高速铁路结合梁桥与列车系统振动分析模型［J］. 华中理工大学学报， 2000， 28（3）： 60-62. GUO Xiangrong， ZENG Qingyuan. Analytical model of the system vibration in high speed combination girder bridge and train［J］. Journal of Huazhong University of Science and Technology， 2000， 28（3）： 60-62.

（编辑 杨幼平）

Effect of wind barrier porosity on coupled vibration of train-bridge system for long-span cable-stayed bridge in crosswind

HE Wei1， GUO Xiangrong1，2， ZOU Yunfeng1，2， HE Xuhui1，2， YANG Zhu1

（1. School of Civil Engineering， Central South University， Changsha 410075， China；2. National Engineering Laboratory for High Speed Railway Construction， Central South University，Changsha 410075， China）

In order to study effects of wind barrier porosity on coupled vibration of train-bridge system in crosswind， by using static aerodynamic coefficients of both the trains at different rail positions and the bridge deck with different pored wind barriers measured by the wind tunnel test， according to the principle of total potential energy with stationary value in elastic system dynamics， the coupling vibration equation of train-bridge system considering the wind load was built up to calculate dynamic responses of trains and bridge of a long-span cable stayed bridge in crosswind. The results show that differences in the influence of wind barrier porosity change from 10% to 40% on the lateral displacement of mid-span between windward conditions and leeward conditions are significant. In windward conditions， the influence of wind barrier porosity changing on the dynamic responses of trains is more significant. Compared with the wind barrier porosity increases from 10% to 20%， the increase of derailment coefficient， rate of wheel load reduction and lateral swaying force of train is more significant when the wind barrier porosity increases from 30% to 40%.

wind barrier； cable-stayed bridge； coupling vibration； dynamic response

U441

A

1672-7207（2016）05-1715-07

10.11817/j.issn.1672-7207.2016.05.034

2015-05-05；

2015-07-15

（Foundation item）：国家自然科学基金资助项目（51322808，51508580，U1534206）；中国铁路总公司科技研究开发计划项目（2015G002-C）；中国博士后科学基金资助项目（2014M562133）；中南大学“创新驱动计划”项目（2015CX006） （Projects（51322808， 51508580， U1534206）supported by the National Natural Science Foundation of China； Project（2015G002-C） supported by the China Railway Corporation；Project（2014M562133） supported by the Chinese Postdoctoral Science Foundation； Project（2015CX006） supported by the Innovation-driven Plan in Central South University）

邹云峰，博士，讲师，从事结构风工程研究；E-mail： yunfengzou@csu.edu.cn