电力电缆的自清除瞬时故障测距研究

成志威，夏向阳，李明德，陈善求，王恺，黄海，王瑞琪，唐洁，黄珂琪

（1. 长沙理工大学 电气与信息工程学院，湖南 长沙，410077；2. 湖南电线电缆产品质量监督检验中心，湖南 衡阳，421001；3.金杯电工衡阳电缆有限公司，湖南 衡阳，421000）

电力电缆的自清除瞬时故障测距研究

成志威1，夏向阳1，李明德2，陈善求3，王恺2，黄海2，王瑞琪3，唐洁2，黄珂琪1

（1. 长沙理工大学 电气与信息工程学院，湖南 长沙，410077；2. 湖南电线电缆产品质量监督检验中心，湖南 衡阳，421001；3.金杯电工衡阳电缆有限公司，湖南 衡阳，421000）

针对目前电力电缆的自清除瞬时故障很难通过传统的过电流保护继电器进行监测，提出一种基于电缆电流、电压测量的单相接地瞬时故障测距方法。通过建立电缆故障模型，采用非负最小二乘拟合法求解故障期间的微分方程组进行故障测距，计算故障距离和故障电阻；然后使用统计工具分析历史故障记录作出最终的故障处理决策；最后应用ATP/EMTP软件进行仿真校验，并在小配电网中验证故障测距算法的有效性。研究结果表明：该算法具有较高的精度，为电力电缆瞬时性故障测距提供了一种新的思路。

故障测距；最小二乘法；自清除瞬时故障

自清除瞬时故障被视为电力电缆潜在性故障发生的前兆，它们持续的时间非常短，并且削弱了电缆绝缘介质的强度，在电缆发生永久性故障前增大了其他瞬时故障发生的频率。在一般情况下，电缆三头是电缆线路的薄弱环节，据统计，约有80%的事故发生在电缆三头上。由此可见，监测电缆接头被水渗透的腐蚀情况对电缆线路的安全运行有重要影响［1-3］。自清除瞬时故障是通过放电能量使电缆绝缘劣化处水汽蒸发消除故障，当电缆接头发生放电时，放电能量能在短时间内导致水汽迅速蒸发，然后发展成高压蒸汽使电弧在很短的时间内被熄灭。在许多情况下，瞬时故障最终发展成永久性故障一般需要数周，因此，若这些瞬时故障能及时正确地被监测和定位，则电网运行工作人员有足够的时间修复或更换有缺陷的配件。国内外许多学者对电缆自清除瞬时故障监测进行了研究［4-9］，然而，对于这种类型的故障测距的研究很少。由于瞬时故障持续时间非常短，无法用传统的阻抗法测距，目前一般采用行波法对瞬时故障测距［10-12］，包括低压脉冲反射法、脉冲电压法、脉冲电流法等。行波法的优点是原理简单，不受故障电阻和线路不对称等因素的影响，但由于对采样频率要求较高，所用设备较多，对设备要求也较高，所以经济性较差。同时，也还存在下列无法解决的问题：1） 反射波识别问题。当电缆线路接头处阻抗不匹配时，反射波的识别将非常困难，而且在近区故障时存在无法识别反射波的死区，且因为波形复杂，需要有经验的专业人员才能对其进行解释，影响了方法的推广。2） 波速不确定性问题。行波波速具有不确定性，影响电缆中波速的因素有导体的电导率、绝缘和土壤状况等。同时该技术需要对多个点进行测量，并且需保证采样时间同步，所以增加了设备投资。通过在时域中求解电流和电压方程计算故障距离，得到一种既简单又经济的方法，这种测距技术在国内已有学者提出［12-16］，但这些研究只简单地考虑了电缆带1个负载的情况，没有考虑负载对测距的影响，并且通常忽视了电缆电容的影响。为此，本文作者通过研究电缆分布电容和负载对测距的影响，提出一种改进的最小二乘拟合算法，并且通过1个小型配电网得到验证。

1 故障测距方法

图1所示为10 kV配电网络电缆线路1发生自清除瞬时故障瞬间，三相电流电压变化情况。从图1可以看出：当电缆发生瞬时故障时，电压和电流之间呈现高度非线性关系，且故障持续时间非常短，只有几毫秒，故障消失后，电流和电压随即恢复正常。

假设电缆A相通过电阻Rf发生接地故障，由于故障持续时间很短，可以认为该电阻是恒定不变的，故障点与安装在变电站的传感器之间的距离为 X。图2所示为电缆发生单相接地故障的等效电路图。

分析图2，电缆A相输入电压和输出电压之间的关系可以表示为

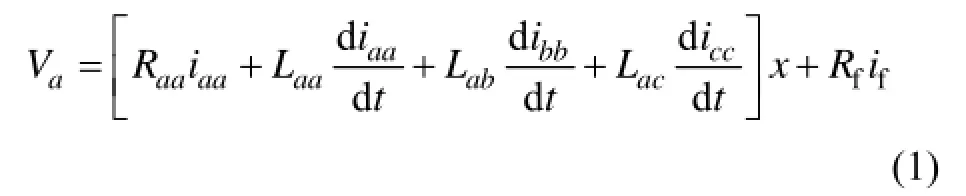
式中： Va为输入端相电压；iaa，ibb和icc分别为A相，B相和C相电流；Raa和 Laa分别为A相单位长度电阻与电感；Lab和 Lac分别为A相与其他相之间单位长度互感；Rf和if分别为故障电阻和故障电流；X为故障点到变电站之间的长度。

另一方面，电流 iaa，ibb和 icc取决于输入端电流ia，ib和ic，如下式所示：

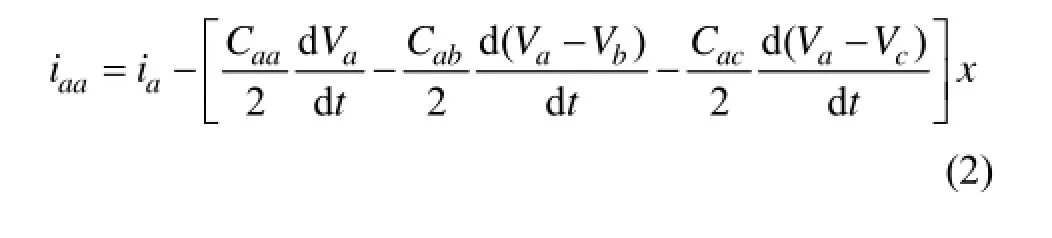
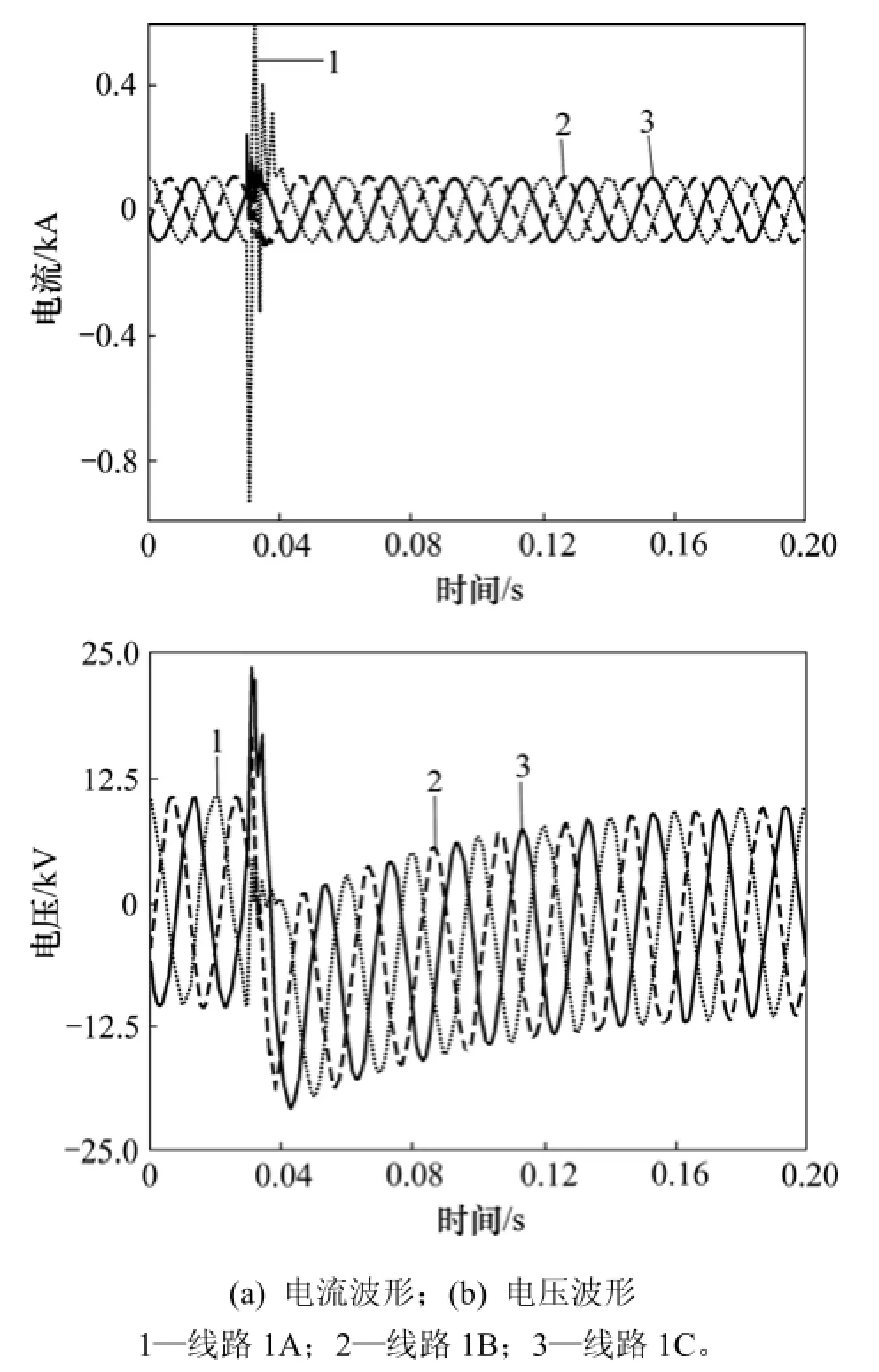
图1 A相自清除瞬时故障电流电压波形图Fig.1 Waveforms of self-clearing transient fault current and voltage for A phase

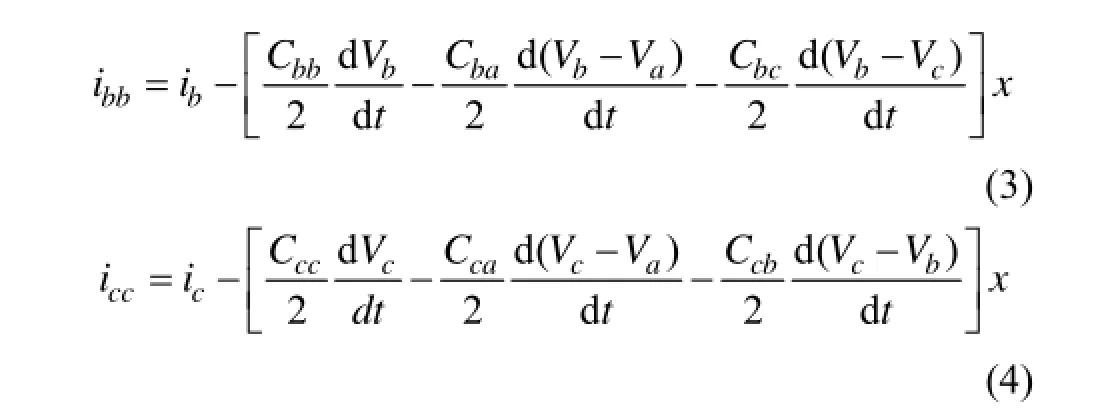
式中： Caa， Cbb和Ccc为单位长度对地电容； Cab， Cac和Cbc为单位长度相间电容； Va， Vb和 Vc为输入端相电压。在电缆发生单相接地故障时，故障电流if等于剩余电流：

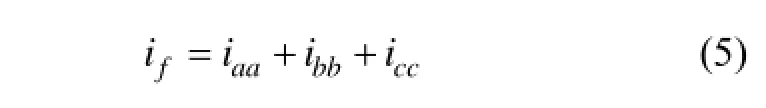
电缆参数Raa， Laa， Lab和Lac可由生产厂家提供或直接测量得到。另一方面，如式（2），（3）和（4）所示，电流iaa，ibb和icc是关于 Va， Vb， Vc，ia，ib，ic和X的函数，其中Va， Vb和Vc以及ia，ib和ic分别通过安装在变电站的电流、电压传感器测量得到。这些参数是故障持续过程中记录存储下的，从故障发生一直到故障消失。式（1）代表1个包含2个未知数（X和Rf）的非线性微分方程系统，微分方程的个数远远大于2，并且取决于故障持续时间和传感器采样频率，因此，要处理1个包含2个未知数的超定方程系统。

采用非负最小二乘法拟合算法计算故障距离，具体流程如图3所示。该迭代方法将非线性微分方程转换为包含2个未知数的线性方程。在每次迭代过程中，方程的数量大于未知参数的数量，2个未知数（X和Rf）可以通过非负最小二乘法拟合得到。然后将计算得到的故障距离与电缆历史故障情况（故障类型、故障时间、故障地点等）进行分析，确定故障发生地点并由控制处理中心采取具体措施，如对故障电缆进行停电检修或进一步监测故障情况。

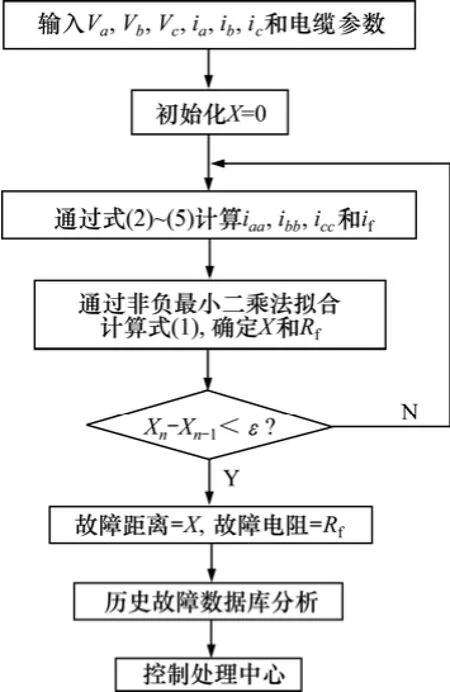
图3 电缆故障测距流程图Fig.3 Flow chart of cable fault location

2 算法有效性检验

为了验证本文提出的故障测距算法，使用ATP/EMTP软件进行仿真。在模型中采用电流、电压测量模块代替电流和电压传感器，然后将所得数据输入Matlab软件进行处理。通过对2种不同情况进行验证：1） 只考虑电缆带1个负载的简单系统，对故障距离、故障阻抗、故障持续时间和传感器采样频率的影响进行研究；2） 考虑负载连接在电缆中间时对测距算法的影响。

通过改变电缆发生单相接地时故障点位置和故障接地阻抗检测算法性能的准确性。

2.1 电缆单端集中负荷

在这个简单的电缆单相接地故障模型中，假设只包含1个大小为 5.0 j5.1+=SMV·A的负载和1根长为10 km的电缆，ATP仿真模型如图4所示。变压器中性点通过1个阻抗为40 Ω的电阻接地。

通过仿真得到的故障测距绝对误差如图5所示，从图5可看出测距绝对误差与故障电阻、故障距离密切相关，其结果取决于故障距离和故障电阻。其中故障电阻与测距绝对误差两者之间线性相关，而故障距离与测距绝对误差则非线性相关，这可由式（1）中非线性变量X进行解释，在最坏的情况下，这个测距算法误差约为0.8 km。

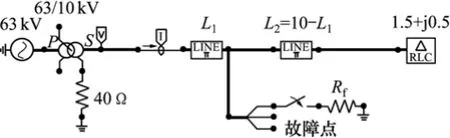
图4 电缆单端集中负荷Fig.4 Load concentrated at cable end

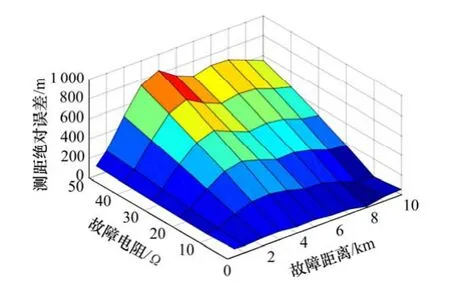
图5 故障距离与故障电阻误差Fig.5 Error versus fault distance and fault resistance

采用非负最小二乘算法计算瞬时性故障距离，方程的数量对算法的性能有重要影响，其数量取决于传感器的采样率和故障持续时间。因此，为了评估传感器采样频率的影响，分别对采样频率为104Hz，105Hz和106Hz进行仿真。图6所示为故障阻抗为0 Ω时获得的结果。从图6可以看出：采样频率越高，所得结果误差越小；当采样频率从104s-1增大到105s-1时，测距误差明显降低，进一步增大采样频率；当采样频率从105Hz增大到106Hz时，误差没有明显降低。对不同的故障阻抗也可以获得相同的结论。

需指出的是：传感器采样频率越高，仿真计算时间也越长，105Hz是兼顾测距性能和计算时间的最佳采样频率，本文的仿真计算都是在这一采样频率下进行的。

图7所示为故障持续时间对故障测距误差的影响。从图7可看出：故障持续时间越长，测距误差越小；故障持续10 ms可以使误差低于0.7 km；当故障持续时间为1 ms时，测距误差可高达1.5 km。

2.2 负载位于传感器和故障点之间

电流、电压传感器安装在变压器低压侧，它们不仅测量故障电流，而且测量负载电流，因此，考虑负载的影响非常重要，尤其是负载位于电流传感器和故障点之间。考虑所带负载位于电缆中间的影响，ATP仿真模型如图8所示。

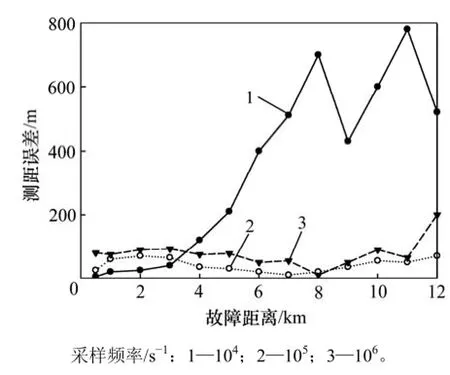
图6 传感器采样频率对测距误差的影响Fig.6 Influence of sensor sampling frequency on location error

图7 故障持续时间对测距误差的影响Fig.7 Influence of fault duration on location error

图9所示为负载连接于图8中位置时对故障计算距离的影响。通过对2个不同故障点F1和F2进行仿真研究，结果显示：随着负载S1的不断增大，故障计算距离都有减小的倾向。

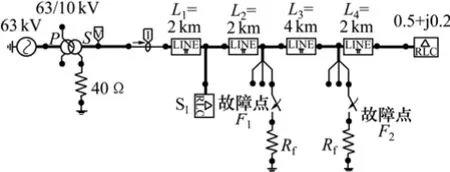
图8 ATP仿真模型Fig.8 Simulation modal of ATP

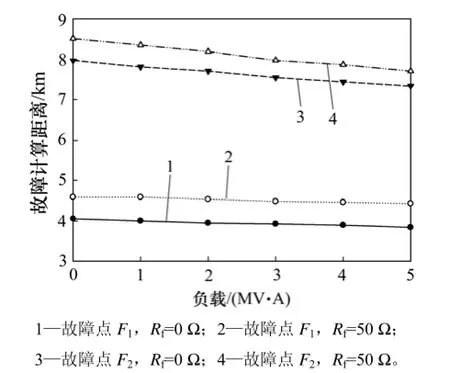
图9 负载连接于传感器和故障点之间的影响Fig.9 Influence of load connected between sensors and fault point

故障发生在F2时，其中故障电阻为50 Ω，当负载从0 MV·A增大到5 MV·A时，故障计算距离减少了0.811 km（从8.549 km至7.738 km），然而，实际故障距离为8.000 km，误差从0.549 km减少到0.262 km。在同等条件下，如果故障电阻接近0 Ω，则计算故障距离从7.990 km减少到7.325 km，在这种情况下误差从0.010 km增加到0.675 km。

从图9可以看出1个几MV·A的负载连接于传感器和故障点之间，可以影响计算故障距离变化几百米，并且由于故障电阻和故障位置的变化，故障测距误差可能变小或者进一步增大。为了考虑负载的影响，可以通过增设电流传感器或者智能电表测量负载电流。

3 小型配电网验证实例

通过1个小型配电馈线（15节点）（如图10所示）对瞬时故障测距算法性能进行研究。系统电压和频率分别为10 kV和50 Hz，变压器（63/10 kV）中性点通过阻抗Z接地，考虑2种接地阻抗：Z=40 Ω和Z=12+j12 Ω，电缆长度和负载如表1所示。分别研究F1～F5等故障点，故障持续时间设定为4 ms，以105s-1采样频率在节点1处测量电压和电流。

表2所示为变压器中性点接地阻抗Z=40 Ω，配电网中电缆不同地点发生瞬时性单相接地故障时，计算的故障距离和故障电阻与实际值的对比结果。从表 2可以看出：各故障点故障距离与故障电阻的计算值与真实值之间误差保持在较小范围内，只有2例测距误差超过1.000 km，分别为点F2（故障电阻为50 Ω时，误差为1.180 km）和 F5（故障电阻为 1 Ω时，误差为1.114 km）。

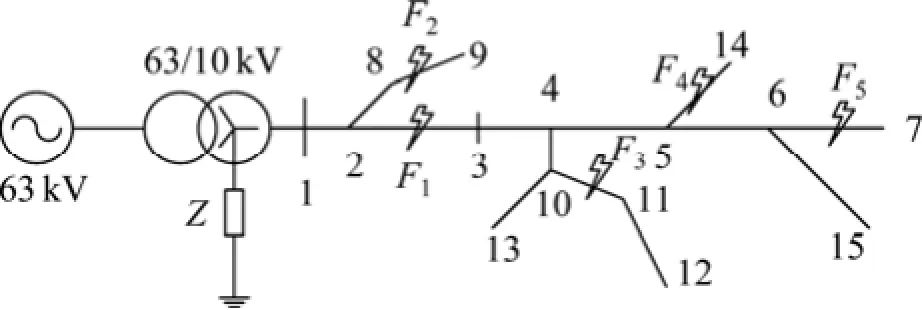
图10 配电馈线分布图Fig.10 Distribution of feeder

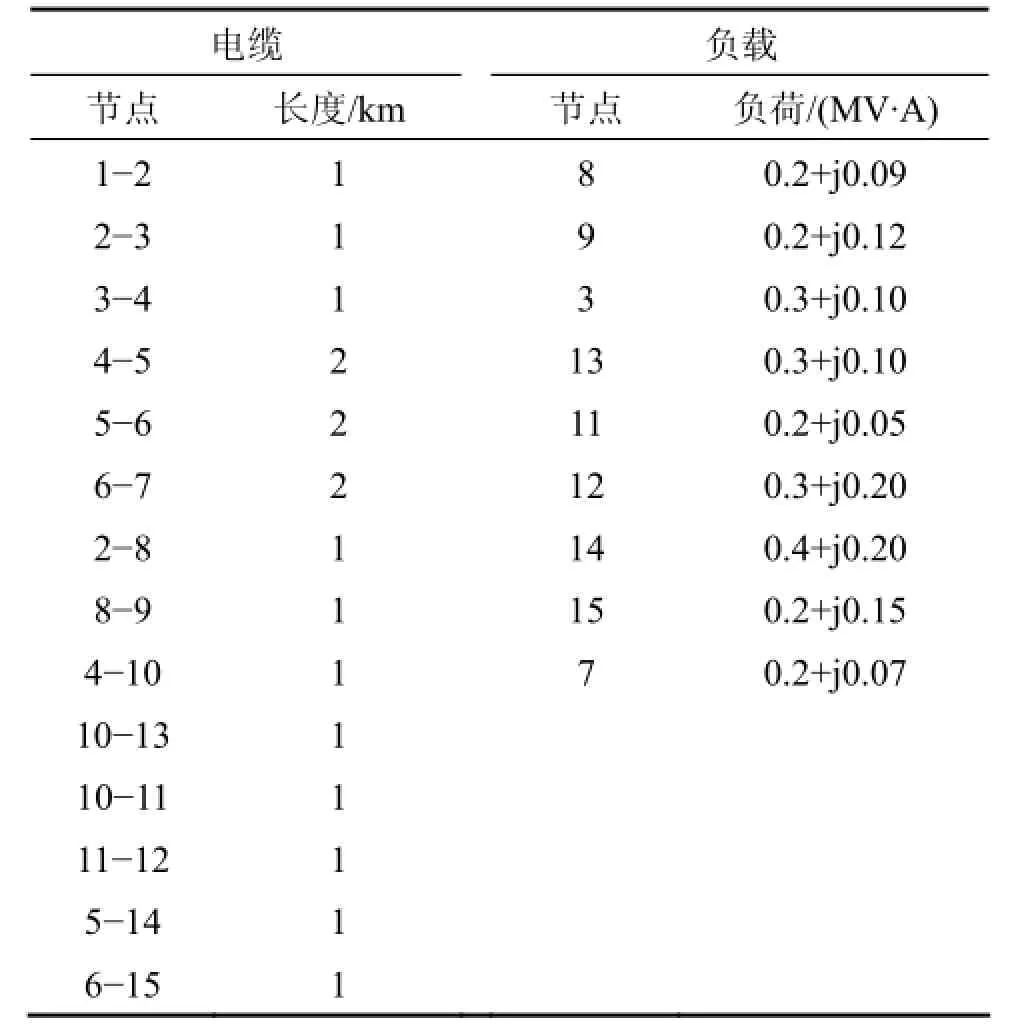
表1 配电馈线参数Table 1 Parameters of configuration feeder

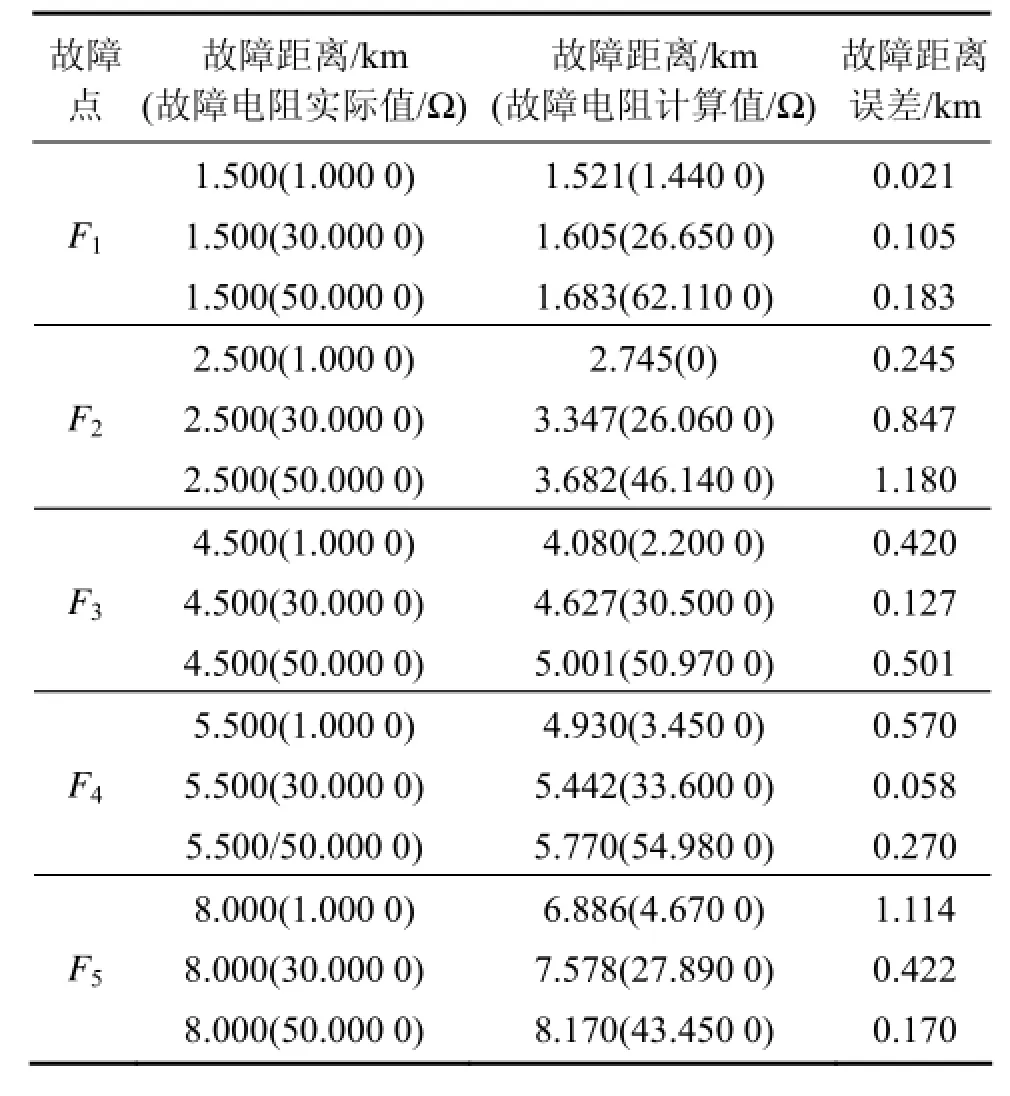
表2 中性点阻抗Z=40 Ω时所得结果Table 2 Results obtained by neutral impedance when Z=40 Ω

当变压器中性点阻抗为Z=12+j12 Ω时，仿真所得结果如表3所示，从表3可见：所得误差大部分低于1.000 km，只有在点F5时，通过1 Ω的故障电阻接地，该算法得到较大误差，为2.750 km。因为上述小型配电网中考虑了负载的影响，所以，仿真计算所得到的测距误差相比于电缆带1个负载时大。

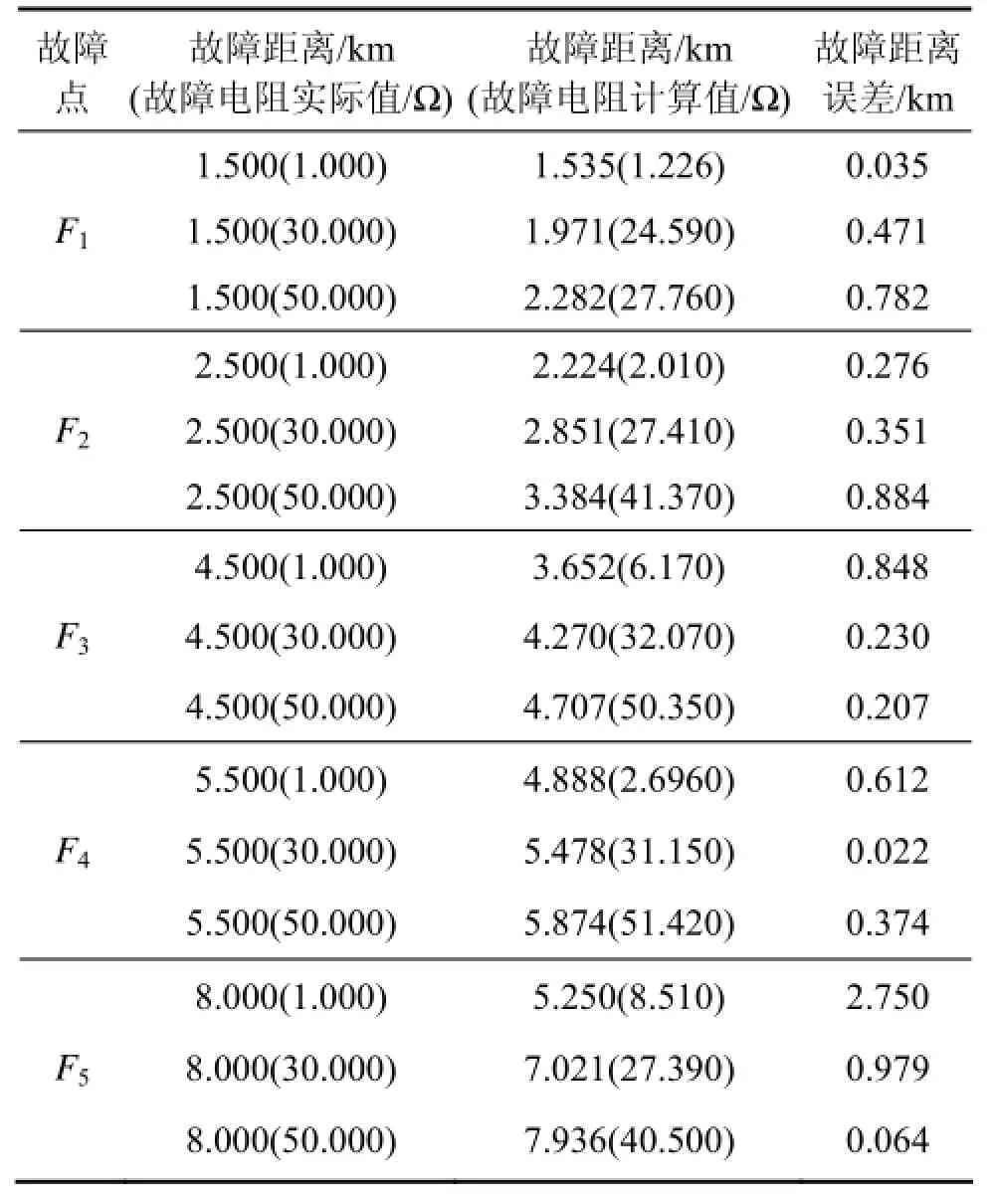
表3 中性点阻抗Z=12+j12 Ω时所得结果Table 3 Results obtained with neutral impedance Z=12+j12 Ω

4 结论

1） 提出一种既简单又经济的方法对电力电缆的自清除瞬时故障测距。采用非负最小二乘拟合算法求解故障期间的微分方程组进行故障测距，并将所得结果结合历史故障情况进行分析，最终由控制处理中心进行决策。其中故障计算距离可以用来确定电缆故障部分，然后采用传统离线方法进一步对故障点精确定位。

2） 通过 ATP/EMTP搭建模型仿真验证了该算法对于不同短路阻抗的准确性，结果表明该算法具有较高的精度，给电力电缆瞬时性故障测距提供了一种新的思路。

［1］ 王新超， 潘贞存. 电力电缆接头故障的预警监测系统［J］. 电力自动化备， 2001， 21（5）： 25-28. WANG Xinchao， PAN Zhencun. Power cable junction monitoring system for fault pre-warning［J］. Electric Power Automation Equipment， 2001， 21（5）： 25-28.

［2］ 古涛， 张乔根. 10 kV交联-油浸电缆中间接头绝缘故障的早期发现［J］. 高电压技术， 2004， 30（36）： 63-64. GU Tao， ZHANG Qiaogen. Early discover of insulation fault of intermediate joint of 10 kV XLPE cable［J］. High Voltage Engineering， 2004， 30（36）： 63-64.

［3］ 杨宁， 姜丰， 孟祥. 基于最小方差温度预报的电缆接头故障预警系统［J］. 电力系统自动化， 2003， 27（24）： 66-69. YANG Ning， JIANG Feng， MENG Xiang， et al. A cable joint fault pre-alarming system based on temperature forecast of minimum variance［J］. Automation of Electric Power Systems，2003， 27（24）： 66-69.

［4］ 刘嫣， 汪梅， 杨存军. 一种新的电缆单端故障测距方法研究［J］. 仪器仪表学报， 2006， 27（6）： 44-45. LIU Yan， WANG Mei， YANG Cunjun. Study on a new method of cable fault location in single terminal［J］. Chinese Journal of Scientific Instrument， 2006， 27（6）： 44-45.

［5］ 张正团， 文锋， 徐丙垠. 基于小波分析的电缆故障测距［J］. 电力系统自动化， 2003， 27（1）： 49-52. ZHANG Zhengtuan， WEN Feng， XU Bingyin. Wavelet analysis based power cable fault location［J］. Automation of Electric Power Systems， 2003， 27（1）： 49-52.

［6］ 郑荣进， 林湘宁， 赵峰. 基于最小相位差全局搜索的高压输电线路故障测距［J］. 电力自动化设备， 2012， 32（3）： 58-61. ZHENG Rongjin， LIN Xianning， ZHAO Feng. Fault location based on global search of minimum phase difference for high voltage transmission lines［J］. Electric Power Automation Equipment， 2012， 32（3）： 58-61.

［7］ EDWARDS A， KANG H， SUBRAMANIAN S. Improved algorithm for detection of self-clearing transient cable faults［C］// IET 9th International Conference on Developments in Power System Protection （DPSP）， Glasgow， United Kingdom， 2008：204-207.

［8］ LONG Zhiling， YOUNAN N H. Underground power cable faul detection using complex wavelet analysis［C］// International Conference on High Voltage Engineering and Application（ICHVE）. Shanghai， China， 2012： 59-62.

［9］ SIDHU T S， XU Zhihan. Detection of incipient faults in distribution underground cables［J］. IEEE Transactions on PowerDelivery， 2010， 25（3）： 1363-1371.

［10］ 熊元新， 刘兵. 基于行波的电力电缆故障测距方法［J］. 高电压技术， 2002， 28（1）： 8-10. XIONG Yuanxin， LIU Bin. Study of fault location method by traveling waves for power cables［J］. High Voltage Engineering，2002， 28（1）： 8-10.

［11］ 张峰， 梁军， 李建超， 等. 基于初始反极性行波检测的单端故障测距算法［J］. 电力系统自动化， 2013， 37（4）： 108-113. ZHANG Feng， LIANG Jun， LI Jianchao， et al. Single ended fault location algorithm based on detection of initial reverse polarity traveling wave［J］. Automation of Electric Power Systems，2013， 37（4）： 108-113.

［12］ 陈玉林， 陈允平， 龚庆武. 基于时频分量相关分析的高压电缆双端行波测距［J］. 电力自动化设备， 2008， 28（12）： 16-20. CHEN Yulin， CHEN Yunping， GONG Qingwu. Double-terminal traveling wave fault location for HV cable based on time-frequency component correlation analysis［J］. Electric Power Automation Equipment， 2008， 28（12）： 16-20.

［13］ 索南加乐， 王增超， 康小宁， 等. 基于线性微分方程参数识别的单端准确故障测距算法［J］. 电力自动化设备， 2011， 31（12）：9-14. SUONAN Jiale， WANG Zengchao， KANG Xiaoning， et al. Accurate fault location algorithm based on parameter identification of linear differential equation with single end data［J］. Electric Power Automation Equipment， 2011， 31（12）：9-14.

［14］ 邢海瀛， 袁汉川， 邓春， 等. 基于分布参数的电力电缆故障定位新型算法研究［J］. 电力系统保护与控制， 2011， 39（14）：16-20. XING Haiying， YUAN Hanchuan， DENG Chun， et al. A novel power cable fault location algorithm based on distributed parameters［J］. Power System Protection and Control， 2011，39（14）： 16-20.

［15］ 刘讯， 黄纯. 蚁群算法在超高压输电线路故障测距的应用［J］.电力系统及其自动化学报， 2012， 24（5）： 132-137. LIU Xun， HUANG Chun. Fault location for EHV transmission line based on ant colony algorithm［J］. Proceedings of the Chinese Society of Universities for Electric Power System and Its Automation， 2012， 24（5）： 132-137.

［16］ 黄小波， 林湘宁， 马晓飞， 等. 适用于集中参数单端测距模型的距离修正方法［J］. 电力系统自动化， 2006， 30（24）： 44-48. HUANG Xiaobo， LIN Xiangning， MA Xiaofei， et al. Improved algorithm for the lump parameter based single-ended fault location models［J］. Automation of Electric Power Systems， 2006，30（24）： 44-48.

（编辑 陈灿华）

Research on self-clearing transient fault location for power cable

CHENG Zhiwei1， XIA Xiangyang1， LI Mingde2， CHEN Shanqiu3， WANG Kai2，HUANG Hai2， WANG Ruiqi3， TANG Jie2， HUANG Keqi1

（1. College of Electrical and Information Engineering， Changsha University of Science &Technology， Changsha 410077， China；2. Hunan Wire and Cable Products Quality Supervision and Inspection Center， Hengyang 421001， China；3. Goldcup Electric Apparatus Hengyang Cables Co. Ltd， Hengyang 421000， China）

Considering that the self-clearing cable transient faults are difficult to be detected by traditional over current protection relays， a method for locating single phase to ground transient faults was proposed based on current and voltage measurements of a power cable. By establishing the model for cable fault system， both distance and fault resistance were estimated. The fault location technique was based on solving a system of differential equations during the fault event， by using nonnegative least square fitting method. The statistical tools and observation history measurement records were used to make fault handling decisions. Finally the algorithm was tested by using ATP/EMTP simulation software， and the proposed fault locating algorithm was validated with a small distribution network. The results show that the algorithm has high accuracy， and provides a new way for transient fault location.

fault location； the least square fitting； self-clearing transient fault

TM247

A

1672-7207（2016）05-1606-07

10.11817/j.issn.1672-7207.2016.05.021

2015-06-10；

2015-08-22

湖南省自然科学基金资助项目（2016JJ5018） （Project（2016JJ5018） supported by the Natural Science Foundation of Hunan Province）

夏向阳，博士（后），教授，硕士生导师，从事电力电子技术在电力系统中的应用和电力设备在线监测等研究；E-mail： xia_xy@126.com