基于坐标变换的无轴承异步电机转子振动前馈补偿控制

杨泽斌，董大伟，孙晓东，金仁，余佩玉

（江苏大学 电气信息工程学院，江苏 镇江，212013）

基于坐标变换的无轴承异步电机转子振动前馈补偿控制

杨泽斌，董大伟，孙晓东，金仁，余佩玉

（江苏大学 电气信息工程学院，江苏 镇江，212013）

为解决无轴承异步电机在高速运行时由机械不平衡引起的转子质量偏心问题，设计一种基于坐标变换的转子振动前馈补偿控制系统。该系统利用旋转坐标变换从位移信号中提取出振动信号，加在原有的径向悬浮力控制系统中，构成1个前馈补偿器，使得控制器给定径向悬浮力信号中同期成分控制力增大，并加大径向悬浮力控制系统对振动信号的刚度，从而强迫转子围绕其几何中心轴旋转，实现转子的振动抑制。研究结果表明：当转速为6 000 r/min时，仿真补偿后转子振动峰-峰值约为11 µm，表明该补偿控制策略能很好地抑制悬浮转子的振动，提高转子旋转精度。该前馈补偿控制方法能够将转子径向位移峰-峰值范围控制在40 μm以内，验证了所提方法的正确性与有效性。

无轴承异步电机；转子质量偏心；振动抑制；前馈补偿控制

无轴承异步电机因具有结构简单、气隙均匀、齿槽脉动转矩低、弱磁范围宽、可采用普通笼型转子等特点，在高速、超高速数控机床、涡轮分子泵、离心泵、高速陀螺、飞轮储能装置等领域具有潜在的应用价值［1-4］。然而由于转子叠片质量分布不均匀以及加工装配精度等机械不平衡原因，都会造成无轴承异步电机转子质量偏心问题，此时会在转子上产生一种与转速同频的激振力。由于这种激振力与转速的平方成正比［5］，当转速达到一定程度时，不仅会使转子发生径向振动，还会造成一部分振动力透过气隙传递到机座上，增大电机噪声，使系统的性能和安全运行受到影响。因此，研究高速转子质量不平衡问题，具有重要的理论价值和现实意义。国内外学者提出了许多质量不平衡补偿方法［6-10］。这些方法可以分为2类：不平衡位移补偿和不平衡力补偿。前者是在一定的转速下减小转子的刚度和阻尼，使转子围绕其惯性轴旋转，而后者是加大悬浮转子的刚度和阻尼，使转子围绕其几何中心旋转。对无轴承电机悬浮转子的振动抑制也取得了一些研究成果［11-14］。年珩等［11］考虑到转子位置偏心问题，采用径向悬浮力闭环控制，缩小了振动位移的峰-峰值，提高了无轴承异步电机悬浮转子稳定悬浮的静、动态性能，但此方法要获得精确的径向悬浮力解析模型；朱熀秋等［12］基于不平衡干扰力的内在特性设计了反馈补偿控制器，在无轴承永磁薄片电机上取得了较好的振动抑制效果，但需要进行大量的数学计算；张倩影等［13］设计了基于最小均方（least mean square，LMS）算法的自适应凹陷滤波器，能够使无轴承开关磁阻电机在不同转速条件下有效补偿转子的同频振动位移，抑制转子的偏心振动，提高了转子悬浮精度，但是决定自适应滤波器稳定性和收敛速度的步长因子难以确定；张涛等［14］基于前馈法设计了不平衡补偿控制系统，对无轴承永磁同步电机转子进行了振动补偿控制，降低了转子振动的幅值，提高了转子的旋转精度，取得了满意效果，但其研究仅仅是在中低速下进行的。本文作者针对无轴承异步电机转子质量偏心振动问题，提出一种基于坐标变换的不平衡前馈补偿器对悬浮转子进行了补偿控制。将坐标变换与前馈补偿器相结合，利用坐标变换提取振动信号，利用前馈补偿器消弱不平衡激振力。在无轴承异步电机转矩和径向悬浮力解耦控制系统的基础上，利用Matlab/Simulink工具箱构建了仿真控制系统，在低速和高速2种状态下进行仿真研究。为进一步验证所提控制策略的有效性和正确性，在无轴承异步电机数字控制系统平台上进行试验研究。

1 无轴承异步电机工作原理及转子动力学模型

1.1 无轴承异步电机的工作原理

在普通的异步电机的定子绕组中再嵌入一套径向悬浮力绕组，其中转矩绕组和径向悬浮力绕组极对数分别为P1和P2；对应的电角频率分别为ω1和ω2。当2套绕组极对数满足P2=P1±1，并且ω1=ω2时，电机中便能产生可控的径向悬浮力［2］。

图1所示为无轴承异步电机（P1=1，P2=2），分别在转矩绕组和径向悬浮力绕组中通入电流I1和I2，则分别产生磁通Ψ1和Ψ2。此时，在气隙上侧Ψ1和Ψ2同向，则此处的气隙磁密增大，而气隙下侧Ψ1和Ψ2反向，故气隙磁密减小，因而产生了沿y正方向的径向悬浮力Fy。当在径向悬浮力绕组中通入反相电流时，便产生沿y反方向的径向悬浮力。同理，如需沿x轴方向的径向悬浮力，则可以通过在径向悬浮力绕组中通入与I2垂直的电流获得。与普通异步电机运行机理一样，无轴承异步电机的转矩也是基于洛仑兹力产生的。

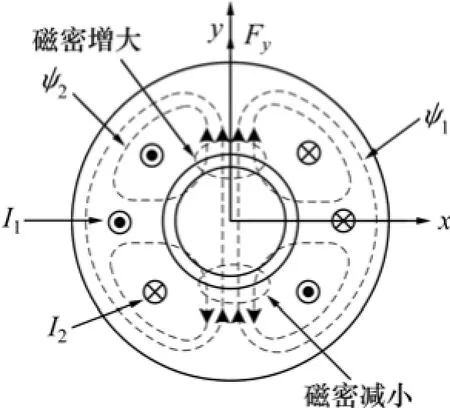
图1 径向悬浮力产生原理图Fig.1 Generation principle of radial levitation force

1.2 悬浮转子动力学模型

对转子进行振动补偿之前，必须对转子的运动轨迹进行分析［8-9］。当转子以角速度ω进行旋转时，若转子存在质量偏心，则会导致惯性轴c和几何中心轴m不重合，图2所示为无轴承异步电机悬浮转子偏心坐标示意图，在xOy坐标系下，转子质心的坐标可以表示为

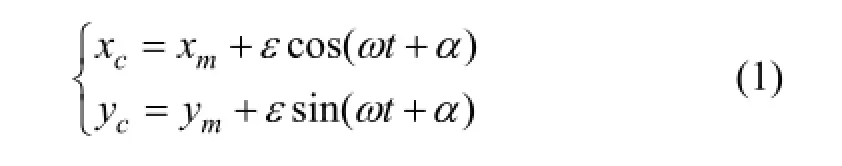
式中：ε为转子惯性轴相对于几何中心轴的偏心距；ω为转子角速度；t为时间；α为初始相角。

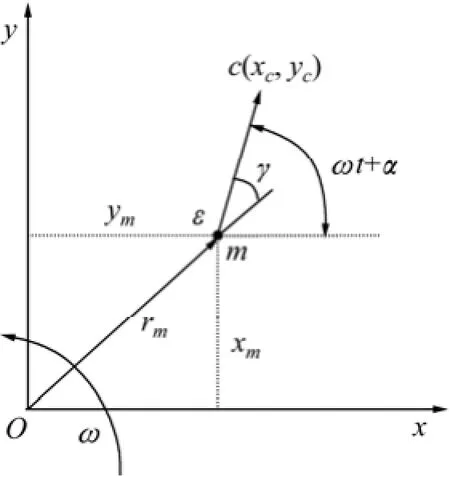
图2 悬浮转子偏心坐标示意图Fig.2 Suspended rotor eccentricity coordinate

为了方便分析，忽略回旋效应，由牛顿运动定律可建立转子的运动方程：

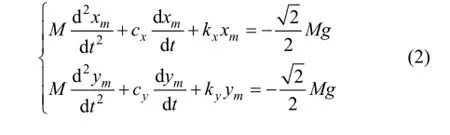
式中：M为转子质量；xm和ym为转子几何中心的运动坐标；cx和cy为耦合参数；kx和ky为刚度系数；等式右边为静态重力项。

当转子质量存在偏心时，式（2）中的右边还要加上离心力项，此时式（2）变为

对式（3）进行求解可得到转子稳定悬浮时的稳态响应：

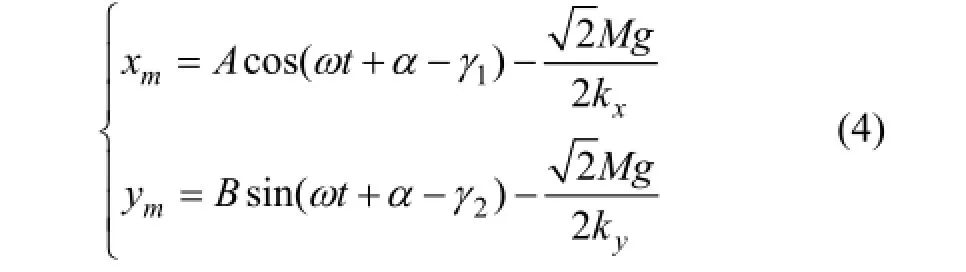
式中：

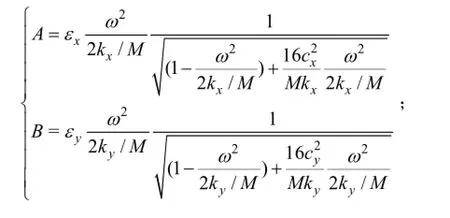
从式（4）可以看出：在转子质量偏心产生的离心力作用下，转子几何中心的运动轨迹为椭圆，当悬浮转子在x和y方向的刚度相等时，转子的运动轨迹为圆。若转子围绕其几何轴旋转时，位移传感器检测得到的偏移信号为零，但当转子质量不平衡存在时，转子在离心力的作用下偏离几何中心轴，位移传感器检测得到的位移信号就包含了转子振动信号。而这个振动信号的幅值与转速的平方成正比关系，当电机在高速或超高速运行时，会有一部分振动力传到机座上，增大电机噪声，影响高速转子系统的性能和安全运行。文中对转子质量不平衡进行补偿控制的原理就是根据位移信号给转子施加1个与不平衡力相反的补偿力，强迫转子围绕几何中心轴旋转，从而实现转子的振动抑制。

2 基于坐标变换的前馈补偿器设计

本文所设计的抑制无轴承异步电机转子振动前馈补偿器，是在气隙磁场定向解耦控制［11，15］的基础上进行的。通过对转子运动轨迹的分析可知：由传感器测得的位移信号中不仅含有与转速同频的振动信号，还有其他一些干扰信号。而所提的补偿控制方法就是将振动信号从位移信号中提出来，加在原有的径向悬浮力控制系统之上，构成1个前馈补偿器，使得无轴承异步电机控制器的给定输出信号Fx*和Fy*中同期成分的控制力增大，从而增大径向控制系统对振动信号的刚度，以达到强迫转子围绕几何中心轴旋转的目的。不平衡补偿控制系统框图如图3所示。

2.1 坐标变换与振动信号的提取

实现转子振动前馈补偿控制的前提就是要从位移信号中提取出与转速同频的振动信号，本文采用旋转坐标变换来实现振动信号的提取。将传感器测得的几何中心位移信号 Xs和 Ys进行从直角坐标到旋转坐标的变换，此时位移信号中与转速同频的振动信号就被

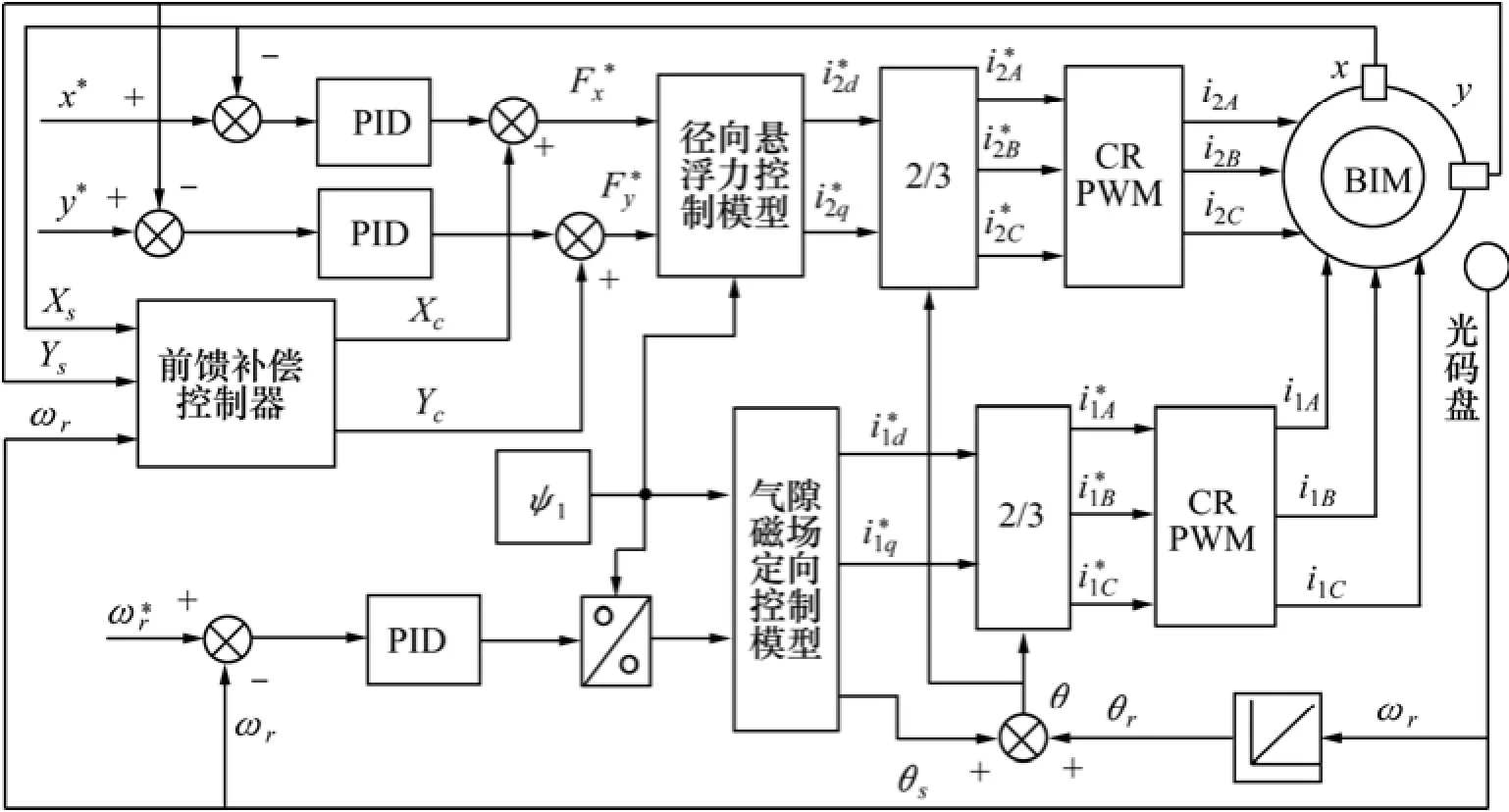
图3 无轴承异步电机转子不平衡补偿控制系统框图Fig.3 Block diagram of rotor unbalance compensation control system for bearingless induction motor

变换为直流量，而与转速不同频的干扰信号经过旋转变换后变为倍频信号，两者之和为 Xr1和Yr1：

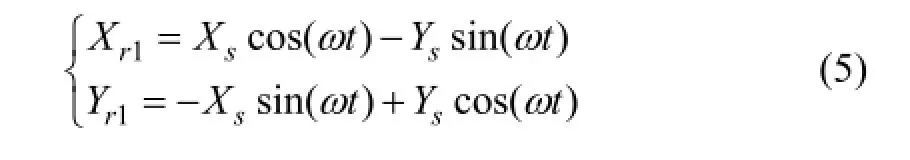
再将上述信号通过低通滤波器，得到输出信号Xr2和 Yr2就只含有直流分量，最后将直流分量进行坐标反变换，便实现了振动信号的提取。

此时的振动信号也就是补偿信号 Xc和 Yc，此信号是与Fzx和Fzy同频同相位的正弦量。通过调节补偿控制器中的比例系数k来改变补偿信号的幅值，从而实现对质量不平衡的补偿。整个过程如图4所示。图4中：T为旋转坐标变换矩阵；T-1为坐标反变换矩阵；C代表低通滤波器。

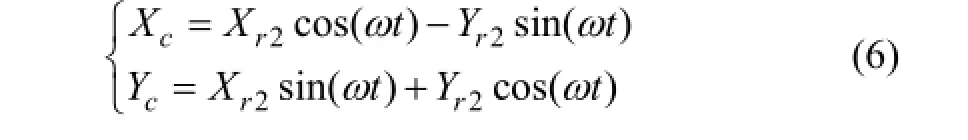
2.2 离心力的计算

由于离心力的存在使转子旋转时偏离其几何中心轴，才导致了振动的产生，所以构建仿真系统时必须考虑离心力的作用。本文只考虑由转子惯性轴与几何中心轴不重合引起的静不平衡，不考虑因惯性轴与几何中心轴有一定角度引起的动态不平衡。假设偏心距为ε，并且电机在x和y方向的位移刚度相同。离心力模块可以根据转子转速的变化，实时地计算出转子角速度ω，作为补偿控制器的输入信号，从而使得离心力的计算具有自适应性。当转子以转速ω旋转时，

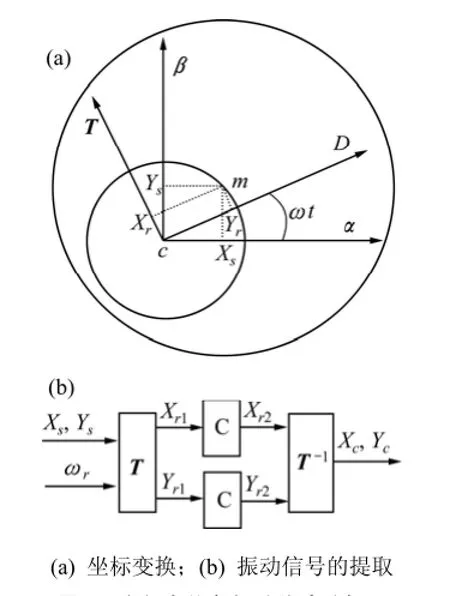
图4 坐标变换与振动信号的提取Fig.4 Coordinate transformation and vibration signal extraction

则作用在转子上的离心力为

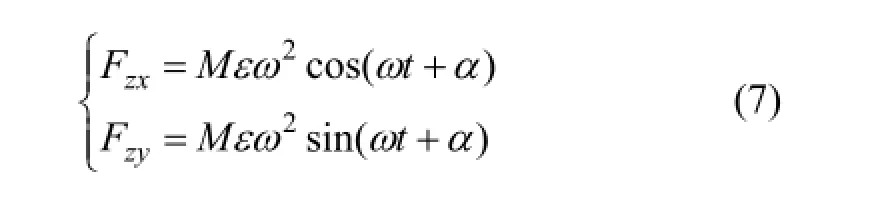
从式（7）可以看出：离心力与转速的平方成正比，即使在偏心距很小的情况下，当转速增大时，离心力也迅速的增大。这也从侧面反映了转子偏心补偿的必要性。

3 仿真和实验研究

3.1 仿真与分析

为验证本文所提基于坐标变换的无轴承异步电机前馈补偿控制方法能在宽速范围内进行振动抑制，利用 Matlab/Simulink工具箱构建了控制系统的仿真模型，在低速和高速2种状态下进行了仿真研究。前馈补偿控制器仿真系统如图5所示，主要包括离心力的计算和振动信号的提取2个部分。

无轴承异步电机的参数为：转子质量M=2.85 kg，转动惯量J=7.69 g·m2；转矩绕组：极对数为P1=1，定子电阻为2.01 Ω，定、转子互感为0.158 56 H，定子漏感为4.54×10-3H；悬浮绕组：极对数P2=2，定子电阻为1.03 Ω，转子电阻为0.075 Ω，定、转子互感为9.32×10-3H，定子漏感为2.67×10-3H，转子漏感为5.42×10-3H；偏心距ε=0.3 mm。仿真结果如图6～8所示。

图6所示为在低速（1 500 r/min）状态下无轴承异步电机转子振动的仿真结果。图6（a）和6（b）所示分别为无补偿控制器转子稳定悬浮时几何中心m在x和y方向的位移波形图，电机转子在稳定悬浮后的振动峰-峰值约为30 µm；图6（c）和6（d）所示分别为有补偿控制器时转子稳定悬浮时几何中心m在x和y方向的位移波形，其振动峰-峰值约为10 µm。从图6可以看出：加上前馈补偿后转子的振动幅值减小，证明了本文所设计控制器的有效性。

图7和图8所示为在高速（6 000 r/min）状态下的仿真结果。图7（a）和7（b）所示分别为无补偿控制器转子稳定悬浮时几何中心m在x和y方向的径向位移波形，电机转子在稳定悬浮后的振动峰-峰值约为 44 µm；图7（c）和7（d）所示分别为有补偿控制器时转子稳定悬浮时几何中心 m在x和y方向的位移波形，其振动峰-峰值约为11 µm。由图7可以得知：当无轴承异步电机运行在高速状态时，本文设计的前馈补偿器能够有效地抑制由悬浮转子质量不平衡而引起的振动，使转子的旋转精度得到大幅度提高。

图8（a）和8（b）所示分别为无前馈补偿器和有前馈补偿器时转子的x和y位移轨迹，由于假设无轴承异步电机在x和y方向的位移刚度相同，从图8可以看出：转子在稳定悬浮后，其几何中心运动轨迹为圆，同时也更清楚地看出所提控制策略的有效性。对比图6和图7的仿真结果还可以发现：无轴承异步电机在低速和高速状态下转子的振动补偿都取得了满意的抑制效果，低速时振动峰-峰值约为未加补偿控制前的1/3，高速状态下转子的振动峰-峰值约为未加补偿控制前的1/4，表明所提抑制方法能在宽速范围内进行补偿控制，尤其在高速时效果显著。

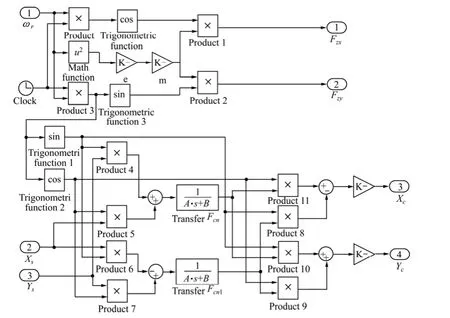
图5 前馈补偿器的仿真模型Fig.5 Simulation model of feedforward compensator

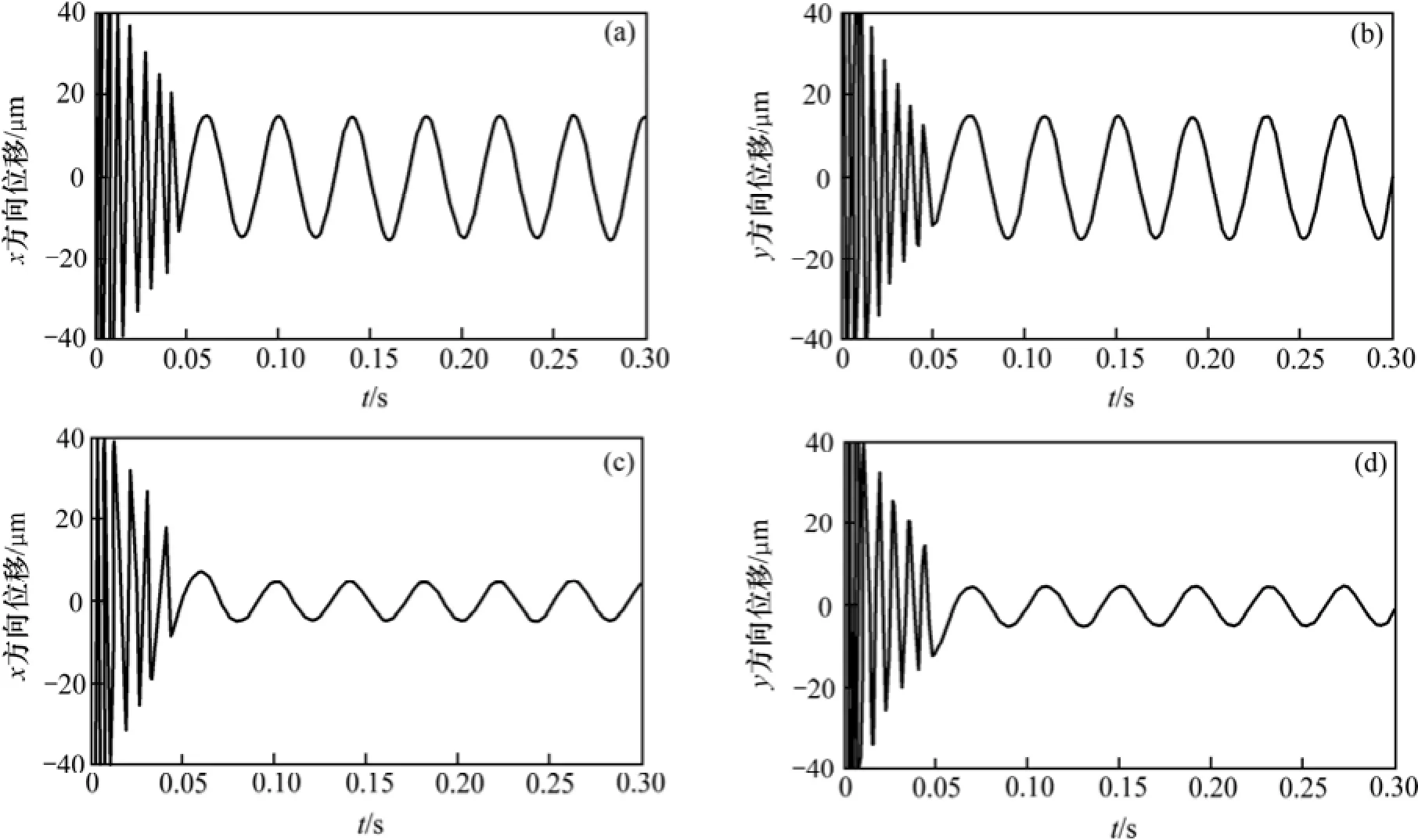
图6 振动抑制仿真结果（1 500 r/min）Fig.6 Vibration suppression simulation results at speed of 1 500 r/min

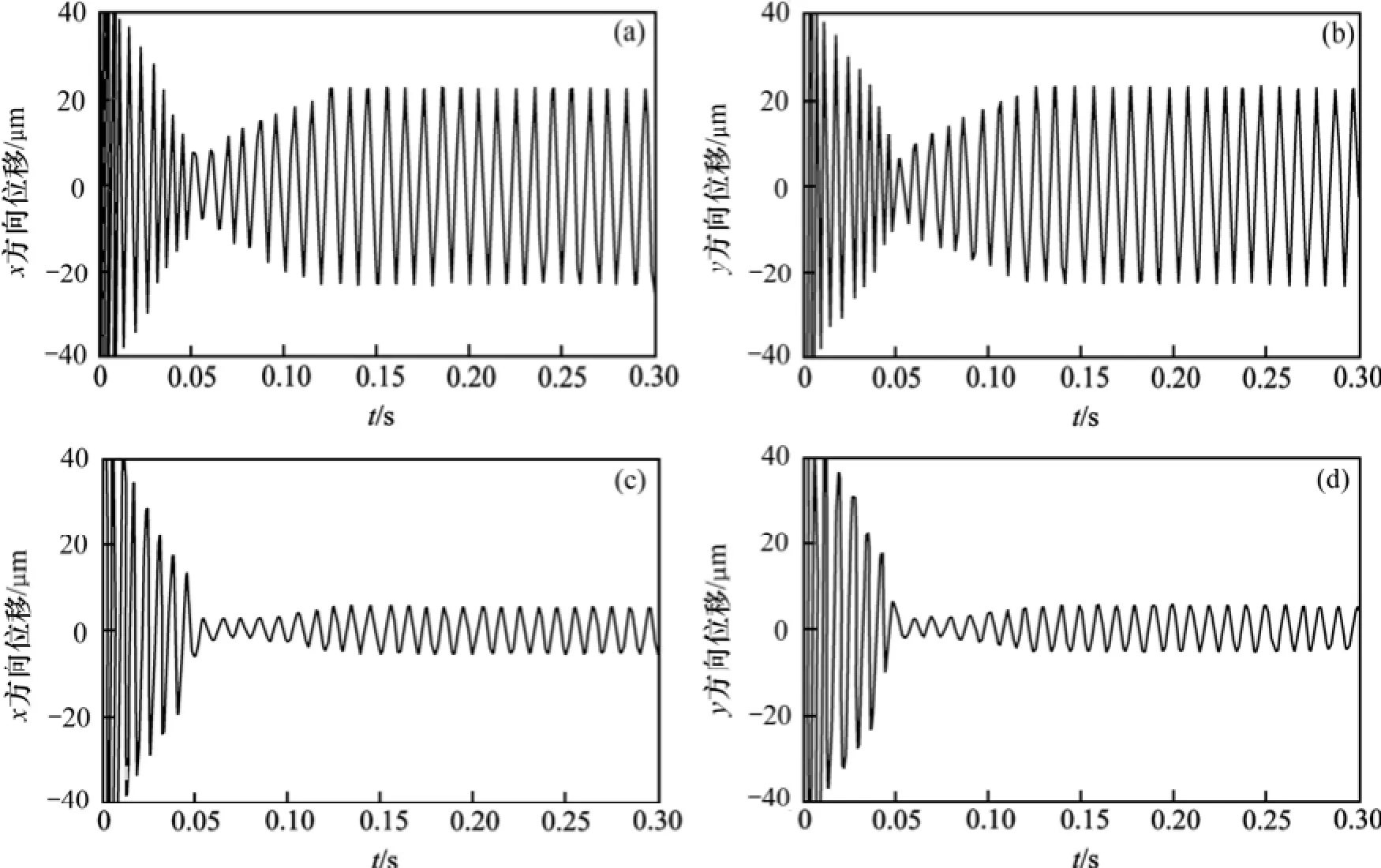
图7 振动抑制仿真结果（6 000 r/min）Fig.7 Vibration suppression simulation results at speed of 6 000 r/min

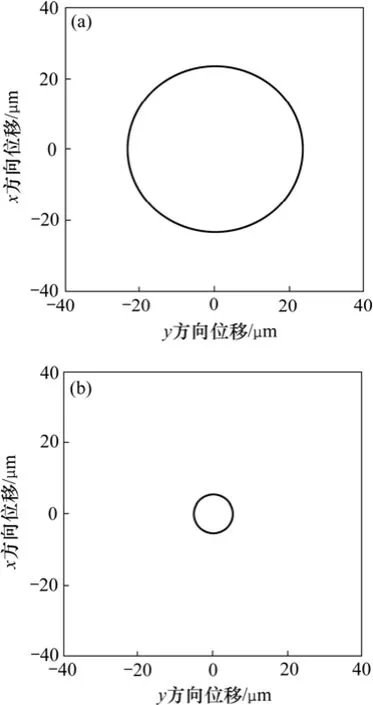
图8 稳定悬浮时转子几何中心的运动轨迹（6 000 r/min）Fig.8 Trajectories of rotor geometry center when stable suspension at speed of 6 000 r/min

3.2 实验与分析

为了进一步证实所提抑制方法的有效性与正确性，以1台二自由度无轴承异步电机样机为实验对象，搭建了以 TMS320F28335为核心的数字控制实验平台，对所提方法进行实验验证，自制样机参数如同仿真参数，实验中电机的给定转速设置为6 000 r/min。实验结构框图如图9所示。

图10（a）所示为无前馈补偿器时x方向上的径向位移。从图10（a）可以看出：振动位移的峰-峰值范围为80 µm，振动范围远小于电机的气隙长度，实现了电机稳定悬浮；图10（b）所示为有前馈补偿器时x方向上的径向位移。由图10（b）可以看出：振动位移的峰-峰值范围在40 µm以内，采用前馈补偿器后，振动幅值减小到原来的1/2左右，抑制效果明显，系统控制精度提高，确保了无轴承异步电机的稳定悬浮工作，验证了所提控制方法的正确性和有效性。

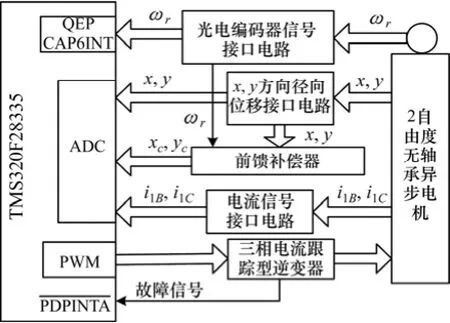
图9 实验结构框图Fig.9 Experimental structure diagram

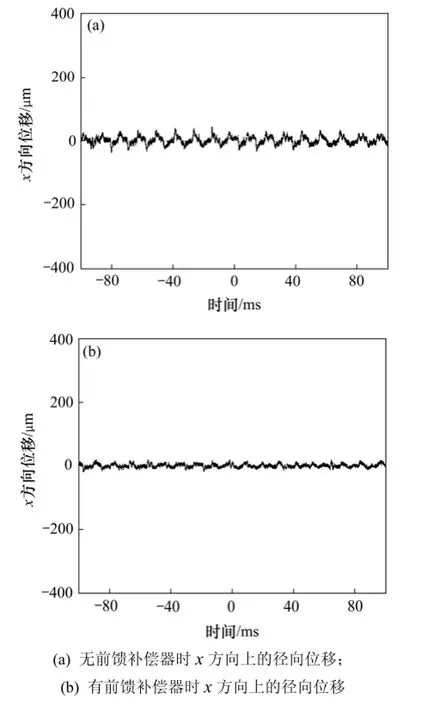
图10 转子振动峰值实验结果Fig.10 Experimental results of rotor vibration peak to peak value

4 结论

1） 采用基于坐标变换的前馈补偿算法对无轴承异步电机转子的质量不平衡进行了补偿控制，该方法能够实时地计算出转子的旋转速度，从而使离心力的计算具有自适应性，实现了对电机的转子质量不平衡进行实时补偿。

2） 该补偿控制方法减小了转子振动峰-峰值，提高了转子的旋转精度，进而验证了前馈补偿控制器对转子振动抑制的有效性。

3） 在低速状态下转子的振动位移约为未加补偿控制前的1/3，高速状态下转子的振动位移约为未加补偿控制前的1/4，6 000 r/min的实验中，转子的振动位移约为未加补偿控制前的1/2，故本文所提方法能在宽速范围内进行振动补偿控制。

［1］ Chiba A， Deido T， Fukao T， et al. An analysis of bearingless AC motors［J］. IEEE Transactions on Energy Conversion， 1994， 9（1）：61-68.

［2］ Chiba A， Power D T， Rahman M A. Characteristics of a bearingless induction motor［J］. IEEE Transactions on Magnetics，1991， 27（6）： 5199-5201.

［3］ SUN Xiaodong， CHEN Long， YANG Zebin. Overview of bearingless induction motors［J］. Mathematical Problems in Engineering， 2014（1）： 1-10.

［4］ 王正齐， 刘贤兴. 基于神经网络逆系统的无轴承异步电机非线性内模控制［J］. 自动化学报， 2013， 39（4）： 432-439. WANG Zhengqi， LIU Xianxing. Nonlinear internal model control for bearingless induction motor based on neural network inversion［J］. Acta Automatic Sinica， 2013， 39（4）： 432-439.

［5］ Sinervo A， Arkkio A. Rotor radial position control and its effect on the total efficiency of a bearingless induction motor with a cage rotor［J］. IEEE Transactions on Magnetics， 2014， 50（4）：1-9.

［6］ Wook J L， Seung S O， Dalho C. Rotor unbalance compensation without angular position sensor for active magnetic bearing［C］// 8th International Conference on Power Electronics-ECCE Asia. The Shilla Jeju， Korea， 2011： 2446-2449.

［7］ Raoul H. Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings［J］. IEEE Transactions on Control Systems Technology， 1996， 4（5）：580-586.

［8］ 虞烈. 可控悬浮转子系统［M］. 北京： 科学出版社， 2003：185-208. YU Lie. Controllable magnetic suspension rotor system［M］. Beijing： Science Press， 2003： 185-208.

［9］ 黄立权， 王维民， 苏奕儒， 等. 基于电磁自愈力的转子自动平衡方法与实验研究［J］. 振动与冲击， 2011， 30（1）： 208-212. HUANG Liquan， WANG Weimin， SU Yirui， et al. Rotor automatical balancing method and test based on electromagnetic self-recovery force［J］. Journal of Vibration and Shock， 2011，30（1）： 208-212.

［10］ 乔晓利， 祝长生. 电主轴-刀具系统不平衡振动的主动控制［J］.振动工程学报， 2012， 25（6）： 651-657. QIAO Xiaoli， ZHU Changsheng. Active control for unbalanced vibration control of electric spindle-tool system［J］. Journal of Vibration Engineering， 2012， 25（6）： 651-657.

［11］ 年珩， 贺益康. 感应型无轴承电机磁悬浮力精确模型及其反馈控制［J］. 中国电机工程学报， 2003， 23（11）： 139-144. NIAN Heng， HE Yikang. Analytical modeling and feedback control of the magnetic levitation force for an induction-type bearingless motor［J］. Proceedings of the CSEE， 2003， 23（11）：139-144.

［12］ 朱熀秋， 郝晓红. 无轴承永磁薄片电机转子不平衡振动补偿控制［J］. 系统仿真学报， 2010， 22（2）： 453-457. ZHU Huangqiu， HAO Xiaohong. Compensation control of rotor unbalance vibration on bearingless permanent magnet slice motors［J］. Journal of System Simulation， 2010， 22（2）： 453-457.

［13］ 张倩影， 邓智泉， 杨艳. 无轴承开关磁阻电机转子质量偏心补偿控制［J］. 中国电机工程学报， 2011， 31（21）： 128-134. ZHANG Qianying， DENG Zhiquan， YANG Yan. Compensation control of rotor mass eccentric in bearingless switched reluctance motors［J］. Proceedings of the CSEE， 2011， 21（31）： 128-134.

［14］ 张涛， 朱熀秋. 无轴承永磁同步电机转子质量不平衡补偿控制［J］. 中国电机工程学报， 2007， 27（15）： 33-37. ZHANG Tao， ZHU Huangqiu. Rotor’s mass unbalance compensation control in bearingless permanent magnet-type synchronous motors［J］. Proceedings of the CSEE， 2007， 27（15）：33-37.

［15］ 王海涛. 无轴承异步电机控制系统研究［D］. 镇江： 江苏大学电气工程学院， 2010： 16-24. WANG Haitao. Control system of bearingless induction motor［D］. Zhenjiang： Jiangsu University. School of Electrical and Information Engineering， 2010： 16-24.

（编辑 杨幼平）

Rotor vibration feedforward compensation control in bearingless induction motor based on coordinate transformation

YANG Zebin， DONG Dawei， SUN Xiaodong， JIN Ren， YU Peiyun

（School of Electrical and Information Engineering， Jiangsu University， Zhenjiang 212013， China）

To solve the rotor mass eccentric problem caused by mechanical imbalance for the bearingless induction motor at high speed， a rotor vibration feedforward compensation control system was designed based on coordinate transformation. The vibration signal was extracted from the displacement signal by rotating coordinate transformation and was added to the original radial suspension force control system. Then， a feedforward compensator was formed，which increased the given period radial suspension force component control signal and amplified the stiffness of the vibration signal of the radial suspension force control system. The rotor vibration was suppressed by forcing the rotor rotating around its geometric center axis. The results show that the compensated rotor vibration peak to peak value in simulation is about 11 µm at the speed of 6 000 r/min. The vibration of suspension rotor can be effectively restrained and the precision of rotor is improved in this control strategy. The presented feedforward compensation control method can make the peak to peak value of rotor radial displacement range within 40 μm. The correctness and effectiveness of the proposed method are verified.

bearingless induction motor； rotor eccentric mass； vibration suppression； feedforward compensation control

TM346

A

1672-7207（2016）05-1543-08

10.11817/j.issn.1672-7207.2016.05.013

2015-05-17；

2015-08-14

国家自然科学基金资助项目（61104016， 51475214， 51305170）；江苏省自然科学基金资助项目（BK20141301， BK20130515，BK20150524）；江苏省“六大人才高峰”项目（2014ZBZZ-017， 2015XNYQC-003）；中国博士后科学基金资助项目（2015T80508， 2014T70482）；江苏大学高级人才科研启动项目（14JDG076）；江苏高校优势学科建设工程项目（2014） （Projects（61104016， 51475214， 51305170） supported by the National Natural Science Foundation of China； Projects（BK20130515， BK20141301， BK20150524） supported by the Natural Science Foundation of Jiangsu Province of China； Projects（2014ZBZZ-017， 2015XNYQC-003） supported by the Six Categories Talent Peak of Jiangsu Province； Projects（2015T80508， 2014T70482） supported by China Postdoctoral Science Foundation； Project（14JDG076） supported by the Professional Research Foundation for Advanced Talents of Jiangsu University； Project（2014） supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions）

杨泽斌，博士，副教授，博士生导师，从事电气装备自动化、磁悬浮传动技术及电机非线性智能控制研究；E-mail： zbyang@ujs.edu.cn