编制数学习题要慎重

戎松魁

《教学月刊·小学版（数学）》2015年第12期刊出了朱学尧老师的题为《续谈人教版教材中“两个习题”的问题——由戎老师〈关〉文引发的思考》一文，文中对笔者发表在《教学月刊·小学版（数学）》2015年第9期上《关于人教版教材中两个习题的探讨》一文进行了质疑。朱老师的质疑精神值得提倡和发扬。

为了说明问题方便，再把两个习题展示如下：

【习题一】 “参赛作品共有125幅，一等奖6幅，二等奖占参赛作品的16%，三等奖的数量比二等奖的数量多4%。提出用百分数解决的问题，并进行解答。”（六年级上册第93页练习19的第10题）

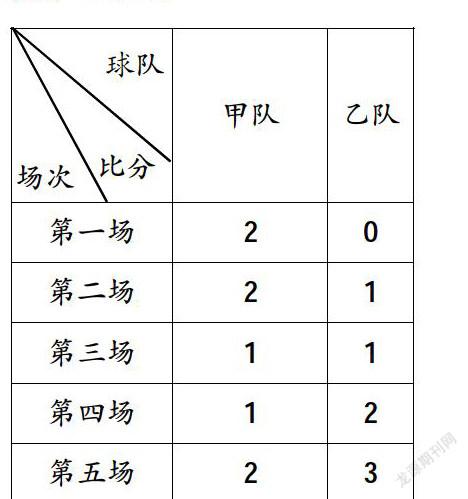
【习题二】 “甲、乙两个足球队之间近期的5场比赛成绩如右表。如果两个队现在进行一场比赛，请预测一下哪个队获胜的可能性大。为什么？”（六年级下册第99页练习21第7题）

一、关于习题一的探讨

对于习题一，已知参赛作品共有125幅，一等奖6幅，由“二等奖占参赛作品的16%”可算得二等奖是20幅。由“三等奖的数量比二等奖的数量多4%”可算得三等奖是20.8幅。对此，笔者提出两点意见：第一点是：“获奖作品数量应当是整数幅，不可能是20.8幅，可见这个习题出了问题。”第二点是：“一般来说，举办一次书法作品或美术作品比赛，在获奖数量分配上，三等奖的数量不可能只比二等奖多4%。”

朱老师对这两点意见都提出了质疑。

对于第一点意见，朱老师提出：“笔者不同意文中所说的，通过列算式：20×（1+4%），计算出三等奖作品数量是个小数，就因此得出习题给的数据有问题的结论。”笔者在仔细阅读朱老师的文章后，并没有找到足以说明习题一“没有问题”的理由。但是文中还是给出了一个解决问题的方法：“即使是先给出一个百分率，但在计算具体数量时，若得不到一个整数，也会采取适当‘取整’的方法。”在很多情况下，这可能也是一个解决问题的好方法。但在习题一中，如果我们将20.8幅适当取整为21幅，然而这样一来，三等奖的数量就比二等奖的数量多5%，而非已知条件中的4%了。如果事先先规定好二等奖（20幅）和三等奖的数量，那也不可能出现“三等奖比二等奖多4%”这样的情况。命题时为什么不直接写“5%”，而要写“4%”，然后再将计算结果“取整”呢？

对于第二点意见，朱老师指出：“戎老师认为，现实生活中三等奖的数量一般要比二等奖数量多。笔者认为，这要取决于评选的方式。”

事实上，在书法作品或美术作品（以“幅”为单位）比赛评奖时，一般来说，评委会会根据参赛作品的数量合理地给出一个一、二、三等奖数量分配的方案，但不管用什么方式评选，一、二、三等奖数量之比不会出现像习题一中“6∶20∶21”（已把“20.8”取整为“21”）那样奇怪的结果，习题一中的数据确实是脱离生活实际的。小学数学练习中有必要编入会得到这样奇怪结果的习题吗？笔者猜测，或许是编者在编写习题时将40%错写成4%了。

事实上，现行教材中出现这种写错数据或写错字的情况也不是“仅此一处”，例如，在六上年级《教