基于工程设计法的移相全桥变换器设计

王 博，赵文春，刘胜道

（海军工程大学 湖北 武汉 430033）

基于工程设计法的移相全桥变换器设计

王 博，赵文春，刘胜道

（海军工程大学 湖北 武汉 430033）

传统的双闭环控制补偿网络的设计依据伯德图进行，工作量大、且需要反复试凑和一定的实践经验，针对以上不足，将调节器的工程设计法引入移相全桥变换器的设计中，进行了系统动态建模并给出了详细的设计过程。利用Matlab/Simulink工具箱对系统输出特性进行了仿真验证分析，同时搭建了试验样机，仿真及试验结果一致，验证了工程设计法在移相全桥变换器的补偿网络设计中的可行性，证明该设计方法合理有效、简化了闭环系统的设计。

移相全桥；工程设计法；平均电流模式；双闭环控制

移相全桥变换器电路结构简洁、控制独特、开关损耗功率小、可实现高功率变换，同时逆变桥开关管的电压和电流应力也可有效降低。闭环系统的建模计算和补偿网络设计是开关电源领域的难点，决定着开关电源的输出电压精度、负载调整率、电源调整率、动态性能等指标，直接关系着系统性能的好坏。开展对该变换器控制补偿网络的研究具有现实意义。

目前设计双闭环补偿网络主要采用借助伯德图设计，需要实践经验和熟练技巧。而变换器各部分可以建立数学模型，简化或近似成低阶系统，经补偿网络实现比例、积分等规律控制，从而处理成少数典型的低阶系统，相关典型环节已做了深入系统的分析，参数计算公式和调节方向都已明确。因而本文将调节器的工程设计方法应用于其中，以简化双闭环移相全桥变换器补偿系统设计，利用Matlab/Simulink工具箱进行了控制系统建模，并对输入电压和负载突变情况进行了仿真。最后制作了试验样机，验证了方法的可行性。

1　基本原理与控制方式选择

图1所示为移相全桥变换器主电路拓扑结构。由超前桥臂（开关管Q1和Q2）和滞后桥臂（开关管Q3和Q4）组成逆变桥，开关管两边分别并联谐振电容（或漏源极电容）和反并联二极管（或开关管的体二极管），Lr是谐振电感（包括串联电感和变压器原边漏感），T是高频变压器。副边采用全波整流，D1和D2是输出整流二极管，Lf和Cf组成了输出滤波电路。超前桥臂超前滞后桥臂一个相位，即移相角，通过闭环控制系统，动态地调节移相角来改变开关管的导通时间，从而调节输出电压电流。控制方式本文选择平均电流模式，移相全桥变换器系统框图如图1所示。

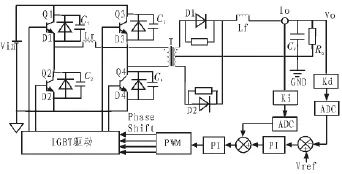
图1　移相全桥变换器系统框图

2　补偿网络的设计

2.1补偿网络结构

图2中，AVR为电压调节器，ACR为电流调节器，α、β为电压，电流采样环节比例系数。Gi（s）为输出电流传递函数，Z（s）为负载。

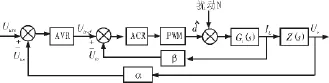
图2　双闭环移相全桥变换器动态结构框图

因PWM装置响应存在延迟，最大时延为一个开关周期T，因此PWM控制和变换器可以看成一个滞后环节。文中开关频率为50 kHz，T=0.02 ms，此滞后环节时间常数较小，可近似认为是一个一阶惯性环节，其传递函数为［3］：

式中：Ks为PWM装置放大系数；Ts为PWM延迟时间，Ts≤T，T为系统周期。

输出电流传递函数为［4］：

式中：n为原副边匝数比，Vin为输入电压，L为滤波电感，Rd为等效电阻。

电流控制环的负载是由输出电容和负载组成的网络，输出电压与电感电流之间的传递函数:

式中C为输出滤波电容，R为负载

2.2电流环补偿网络的设计

从静态要求看，希望系统电流是恒定的，与给定无静差。从动态性能考虑，希望电流环不要有太大的超调，所以电流环应以跟随性能为主，校正成典型Ⅰ型系统，显然应采用PI型电流调节器，其传递函数可写成:

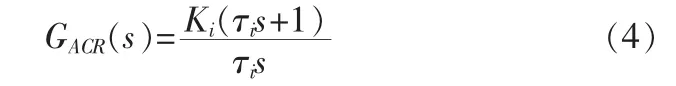
式中：Ki为电流调节器的比例系数，τi为电流调节器超前时间常数。

电流环开环传递函数为：

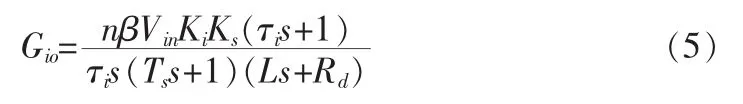
为了让调节器的零点与控制对象的大时间常数极点相消，选择τi=L/Rd

则开环传递函数为：

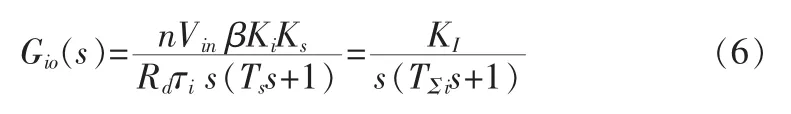
式中：KI为电流环开环增益，TΣi为惯性环节时间常数。

电流调节器参数由Ki和τi决定，τi是控制对象本身固有的，已经选定Ki，可依据系统动态性能的要求选定，其值越大，系统响应速度越快但相角稳定裕度越小，选择参数时需要折衷考虑快速性和稳定性。本系统希望电流环超调量σ≤5％，则选择将工程器设计成二阶最佳系统，选择衰减系数ξ=0.707，代入数字则可得Ki=0.16。电流环的开环传递函数为：

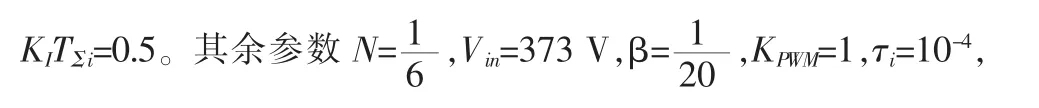
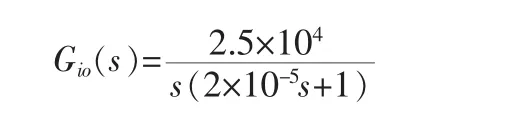
补偿后电流环开环传递函数伯德图如图3所示，电流环的低频段以-20 dB/dec的斜率下降，增益为30 dB；中频段中频段斜率为-20 dB/dec，并且占据较宽的带宽，相角裕度为65.5 deg，符合表 1特性，裕度充足，稳定性良好；高频段以-40 dB/dec下降，系统衰减快，抗干扰能力强。

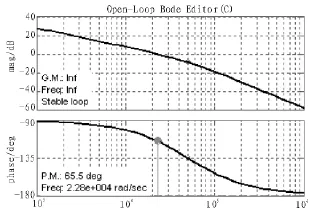
图3　电流环开环传递函数伯德图

电流环等效闭环传递函数为：

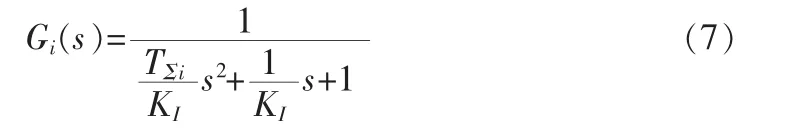
代入数值得：

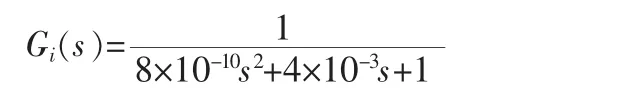
经验证符合近似条件，接入电压环中，因等效环节输入量变化，电流环在电压环中处理为：

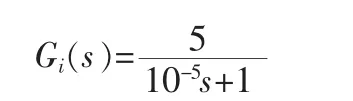
经验证符合斜坡匹配标准，PWM比较器能正常工作。电流环由开环的双惯性系统调整为一阶惯性环节，闭环控制改善了控制对象性能，加快了局部的跟随作用。

2.3电压环控制器设计

考虑电压环稳态和抗扰性能的要求，将其校正成典型Ⅱ型系统。传递函数为：

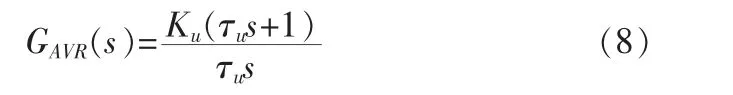
式中：Ku为电流调节器的比例系数，τu为电流调节器超前时间常数。

开环传递函数为：

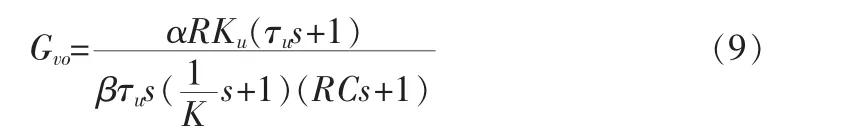
化为：

式中：KU为电流环开环增益，TΣu为惯性环节时间常数。电压调节器参数由KU和τu决定，按照典型Ⅱ型系统参数关系有：

式中h是斜率为-20 dB/dec的中频段宽度。h越小，上升时间tr越快，h越大，超调量σ越小，调节时间ts变化为非线性。h越大，动态降落ΔCmax越大，最大动态降落时间tm和恢复时间tV都越长，抗干扰性能越差。文中综合指标考虑跟随性和抗扰性，选择h=5。依据公式：

代入数据可得KU=7.5×103，则有Ku=0.375，τu=2×10-2，电压环开环传递函数：

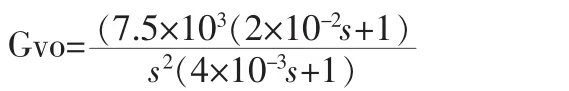
由图4所示电压环开环传递函数伯德图可知系统相角裕度为41.1°，系统的稳定性符合要求。

图4　电压环开环传递函数伯德图

3　仿真与实验

3.1仿真

文中使用Matlab/Simulink建立了移相全桥变换器平均电流模式的双闭环控制仿真模型。移相全桥变换器主电路如前图1所示。输入直流电压Uin=540 V；输出直流电压Uo=28.5 V；输出直流电流Io=400 A；谐振电感13；谐振电容4 nF；输出滤波电感L=160；输出滤波电容C=3 300 μF；工作频率f=50 kHz，负载R为0.071 25 Ω。

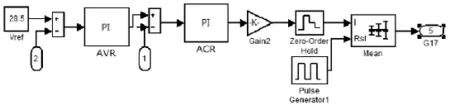
图5　双闭环PI反馈控制模型

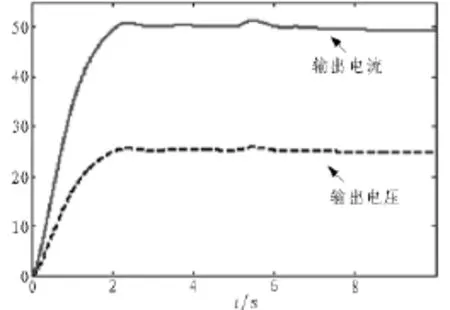
图6　电压突变时输入电压与输出电流波形

平均电流模式双闭环PI反馈控制模块如图5所示，系统输出电压经采样网络采样后 （图5中输入2）与参考信号Vref进行比较、经补偿器AVR补偿后为电流环提供一个参考信号。ACR为电流控制器，将电感电流经电流采样器转换的电压信号（图5中输入1），与参考电压进行比较、补偿，产生控制电压信号，输入PWM移相发生模块调节系统占空比，从而控制系统输出。

输入电压突变时输入电压与输出电流波形如图6所示，系统初始时输入电压为540 V，电压输出最大值为25.45 V，超调量为1.8％，3.7 s达到稳定输出。5 s时系统输入电压突变为600 V，输出电压波形最大值为25.75 V，恢复时间约为1.5 s，调节过程平滑且无波动。

3.2实验

为进一步验证系统设计的正确性，设计了一套移相全桥ZVS变换器，由EMI滤波电路，输入整流滤波电路，主功率变换电路（包括桥式逆变电路、谐振网络、高频变压器）、输出整流滤波电路、反馈控制电路、驱动电路、保护电路等几部分组成。主功率开关管选择MOSFET，型号为HIT公司的K1522，芯片采用移相全桥变换器专用UCC3895，补偿网络的放大器选择LM358，输出整流二极管选用ON公司的MURP20040CT快恢复二极管，其余参数依据仿真结合实际进行部分调整。实验结果如下：

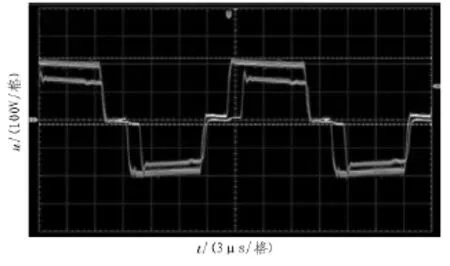
图7　Uab与变压器次级波形

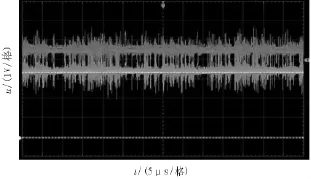
图8　电压和电流反馈信号波形

由图7可以看出，原边波形很干净，副边占空比明显小于原边，这是移相全桥变换器特有的占空比丢失，一个周期占空比丢失时间为1.8 μs，占空比丢失Dloss为8.5％。本电源为抑制输出整流管电压震荡，采用并联RC缓冲支路，以将谐振电感中多余的能量消耗在RC支路上。副边整流管电压波形可以看出，变压器副边整流输出电压的电压尖峰不到输出电压幅值的1/5，震荡次数少，电压尖峰和高频寄生振荡都得到了很好的抑制。图8所示为电压和电流反馈信号波形，上方为电压反馈输出，下方为电流反馈输出。可知系统反馈信号及输出电压电流稳定，系统运行可靠，满足设计需求，但纹波较大，今后需进一步研究处理。

4　结　论

文中介绍了基于调节器工程设计法设计的平均电流模式控制的移相全桥变换器设计过程，同时结合MATLAB软件中的 Simulink仿真平台对其进行了系统建模，并对系统输入电压和负载突变等情况进行了仿真研究和实验验证，仿真和实验结果验证了设计的正确性，表明基于工程设计法设计调节器可依据系统预想的性能指标直接选定参数，过程简便，操作性强，简化了闭环系统的设计。

［1］李宏，荣军.峰值电流控制在移相全桥变换器中的技术研究［J］.电力电子技术，2008，42（1）：81-83.

［2］梁永清，黄志强.双闭环控制的移相全桥软开关变换器的研究［J］.现代电子技术，2014，37（8）：156-158.

［3］陈伯时.电力拖动自动控制系统［M］.北京：机械工业出版社，2003.

［4］阮新波.脉宽调制DC/DC全桥变换器的软开关技术［M］.北京：科学出版社，2012.

［5］Hyuntae Choi，Mihai Ciobotaru，Vassilios G.Aglidis cascaded h-bridge converter with multiphase isolated DC/DC converter for large-scale PV system［J］.IEEE International Conference on Industrial Technology，2014，8（14）:455-461.

［6］张敬南，姚绪梁，张强，等.基于工程设计法的双向直流变换装置的设计［J］.电力电子技术，2010，44（9）：83-26.

Phase-shifted full-bridge converter based on engineering design method

WANG Bo，ZHAO Wen-chun，LIU Sheng-dao
（Naval University of Engineering，Wuhan430033，China）

The traditional double closed-loop control system compensation network design based on the Bode diagram，with heavy workload，trial and some practical experience.The Engineering design method of the regulator is introduced into the design of phase-shifted full-bridge converter.The dynamic modeling of the system is carried out and the design procedure is given.The simulation was carried out with Matlab/Simulink toolbox，and the experimental prototype was constructed.The feasibility of the method is verified，and the design method is proved to have a reasonable and effective design of the closedloop system.

phase-shifted full-bridg；engineering design method；average current mode；double closed-loop control

TN8

A

1674－6236（2016）16-0043-04

2015-08-21稿件编号：201508115

国家自然科学基金资助项目（51377165）

王 博（1990—），男，山西定襄人，硕士研究生。研究方向：开关电源、智能控制。