组合评价模型在医药供应商评级中的应用

陶玉琪，杨立洪

（华南理工大学 数学学院，广州 510640）

组合评价模型在医药供应商评级中的应用

陶玉琪，杨立洪

（华南理工大学 数学学院，广州 510640）

随着医药企业药品购销和管理模式的不断变化，供应商评级作为企业进行供应商选择、管理、监督和改善等一系列活动的基础和标准，显得越来越重要。本文主要从医药供应商入手，提出基于层次分析的有序多分类Logistic组合评价模型，在层次分析模型的基础上，利用有序多分类Logistic模型来修正评价结果并得到相应的概率值。该模型可用于从不同要素间比较系统、全面地评价医药供应商的整体水平。

供应商评级；组合评价模型；层次分析

0　引 言

G企业是一家集科研、生产、销售为一体的大型医药流通企业，有供应商企业1 530家，已经在产权结构、运营模式、管理制度、业务流程上达到了一定水平并形成了自身的特色。但是，G企业对供应商的管理还存在一些需要改进的地方，如：对供应商的淘汰尽管考虑合格率、交货准时率、服务等方面，但多以主观因素为主；多方引进经销商，但多数经销商素质低，且其技术水平不能支持新药品的开发要求；高定位的价格水平不能满足新药品的目标成本等。现G企业急需对这众多供应商进行评价，为G企业分层管理经销商提供有力的决策支持。

由于供应商的评价指标是由定性和定量指标构成，目前企业较多采用的是定量和定性相结合的层次分析法或有序多分类Logistic回归模型，层次分析法简洁实用，容易为决策者所使用，但层次分析法需要行业专家对各层指标的权重进行赋值，因而不同程度地存在人为痕迹；有序多分类Logistic模型因其适应性较高并能得到相应的概率值常被用于解决分类问题，而对供应商的评价属于无监督学习，前人往往会采取专家对一部分供应商进行打分，然后将这一部分供应商的数据作为训练样本建立Logistic回归模型，但当总样本规模过大时，操作起来太过繁琐，最后可能由于训练样本的规模过小而导致模型的拟合效果欠佳。邢鑫鑫在《突发事件铁路应急预案组合评价方法研究》中提出基于层次分析的神经网络组合评价模型，将其应用于铁路应急预案评价中既积累了专家的知识与经验又可以避免评价过程中人为因素导致的失误。本文提出的基于层次分析的有序多分类Logistic组合评价模型不仅综合了之前组合模型的优点，而且还具备有序多分类Logistic模型的优势。

1　供应商评价指标体系模型

通过总结一些先进企业的管理实践，同时考虑到指标的实用性，综合G企业所提供的信息，本文提出了一个具有11项指标的供应商评价体系。该指标体系适用于医药企业的主要供应商的评价，在具体应用中企业可根据实际情况，对细化的指标层进行修改。

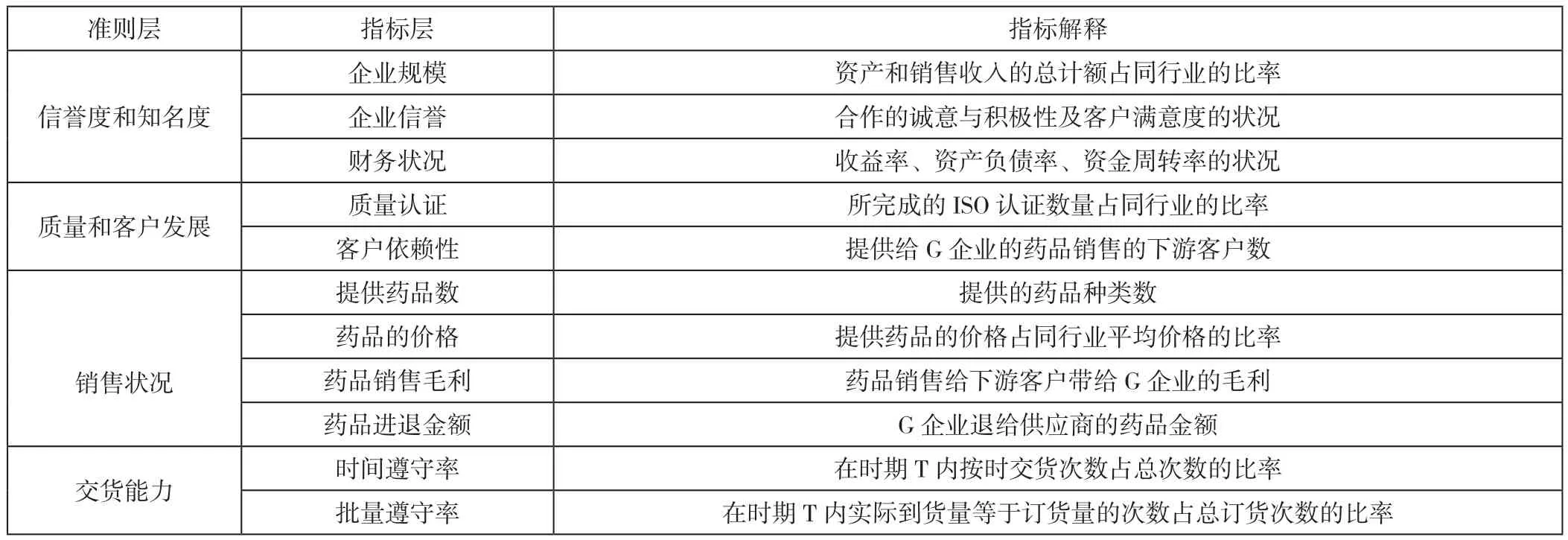
表1　供应商评价指标

2　组合评价模型

该组合评价模型的主要思想为：首先，利用层次分析法确定各个指标的权重，借此得到各个指标的综合评价值。然后，构建Logistic回归模型，把指标值和综合评价值作为回归的解释变量和响应变量的取值，通过最大似然估计所得到的回归系数就积累了专家的知识和经验，这样可以避免评价过程中人为因素导致的失误，提高评价的准确性。

2.1层次分析法

层次分析法（AHP）是一种定性与定量相结合的多目标决策分析方法，能够有效地分析目标准则体系层次间的非序列关系，综合决策者的判断和比较。层次分析法的具体步骤如下。

（1）根据表1的供应商评价指标体系，对应的分为目标层、制约主要素层、制约子要素层。

（2）构造两两判断矩阵。按照层次结构模型，从上到下逐层构造判断矩阵。每一层元素都以相邻上一层次各元素为准则进行两两比较，按重要性程度进行赋值，在赋值时采用AHP方法的创始人T.L. Satty教授提出的1-9标度法，建立制约主要素层相对目标层的判断矩阵A，制约子要素层相对制约主要素层信誉度和知名度、质量和客户发展、销售状况以及交货能力的判断矩阵B1、B2、B3、B4。

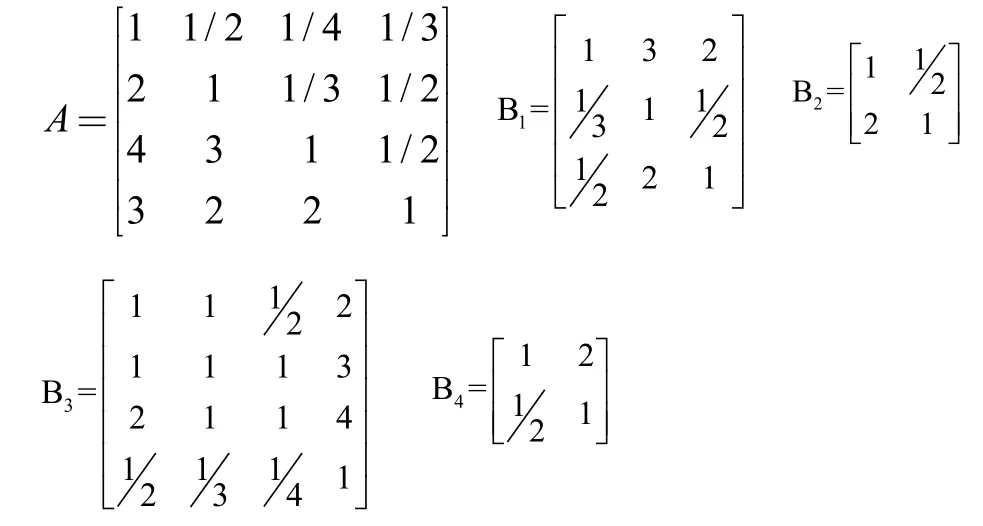
（3）单层次排序及一致性检验通过方根法计算出判断矩阵A的特征向量，确定制约主要素层各指标相对目标层的权重w=（0.0974，0.1638，0.3375，0.4013）T，一致性指标C.I=0.0574＜0.1说明A通过了一致性检验。同理，对制约子要素层的4个判断矩阵B1、B2、B3、B4进行一致性检验并求得相对于制约主要素层的相对权重：

最终确定出制约子要素层的指标对于目标层的综合权重W：

（4）计算综合评价值利用公式，计算综合评价值。公式如下：

式（1）中，Tj表示第j个供应商的综合评价值，Cij表示第j个供应商的第i个指标的指标值，在实际操作中把每项定性或定量评价指标分为差、中、良、优4个等级，对应的Cij分别设为30、50、70、90。

2.2有序多分类Logistic回归模型

Logistic回归分析法作为量化企业信用风险的一种主流方法，不仅灵活简便，而且其许多前提假设比较符合经济现实和金融数据的分布规律。譬如不要求模型变量间具有线性相关关系，不要求变量服从协方差矩阵相等和残差服从正态分布等，这使得模型的分析结果比较客观。

在广泛征询G企业管理员意见的基础上，需要将供应商评为优、良、中、差4个等级。y（y=1，2，3，4）表示供应商的4个等级（4表示优，3表示良，以此类推），此时解释变量就是有序多分类变量。

有序多分类Logistic模型的定义如下：

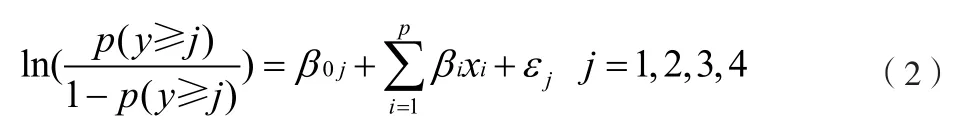
式（2）中，p为影响变量的个数，xi（i=1，2，…，p）为指标值，εj～N（0，1）。

有序多分类Logistic回归模型的建模具体步骤如下：

（1）样本数据规范化处理把各个供应商企业对应的指标值还原为差、中、良、优4个等级，同时对综合评价值采取单指标聚类的方法划分为差、中、良、优4个等级，这4个等级对应的取值为1、2、3、4。将层次分析结构中制约子要素层的变量作为Logistic回归模型的预测变量xi（i=1，2，…，11），层次分析法得到的综合评价结果作为响应变量y。

（2）回归系数的估计及显著性检验利用极大似然估计，可以算出公式（1）中回归系数的估计值，其中7个影响变量的回归系数在显著水平10%下满足检验（P值小于0.1），分析结果如表2所示。

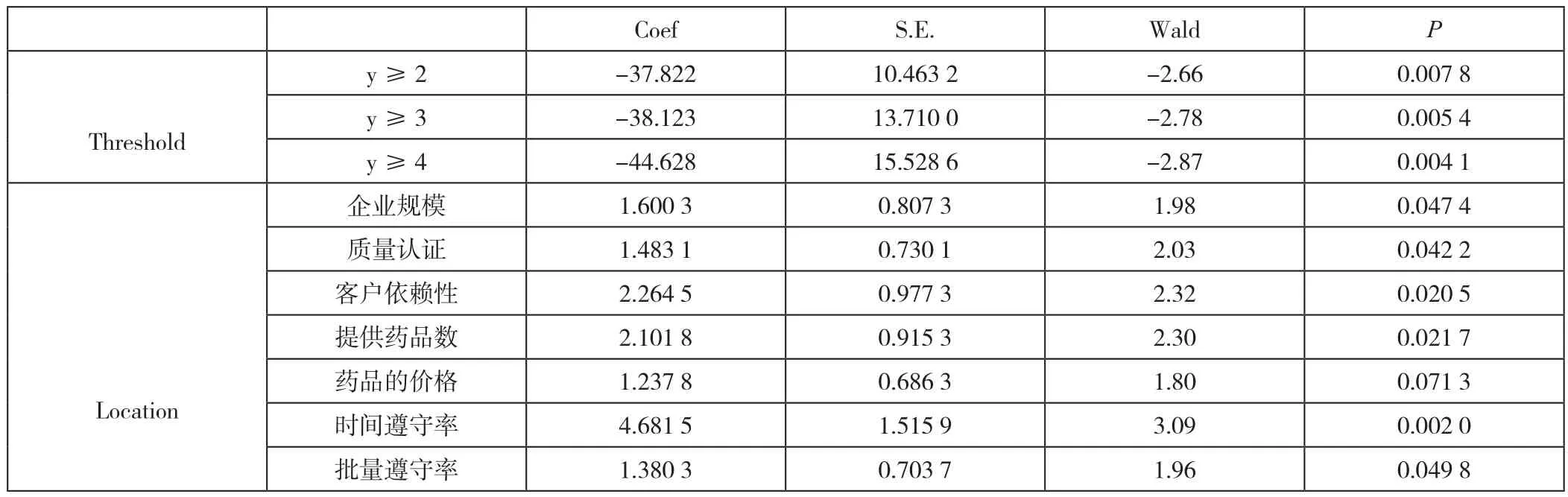
表2　参数估计

（3）计算概率值将各回归系数值带入公式（2）即可估算出：

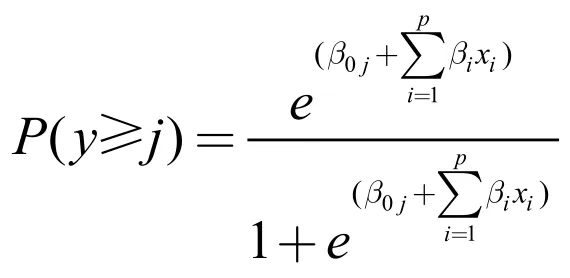
则各供应商属于各个等级的概率值可表示为：

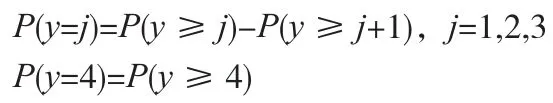
取概率值最大的那个等级即为供应商企业的评级结果。

2.3结果的分析与应用

时间遵守等级的回归系数为4.681 5，在各个预测变量中是最大的，对应的优势比这表明随着时间遵守等级的上升，供应商的综合评价属于较高级别的概率将增大得最快，该结果符合G企业对供应商“时间遵守高于一切”的评价原则。对于企业而言，可将建立好的基于层次分析的有序多分类Logistic组合评价模型可对供应商进行合理的管理，如：G企业计划新药引进以评价等级为优的供应商为主，其他为辅；根据评价等级重新确定药品供应商的销售份额和回款时间，中、差级供应商超销售份额时，超额部分转优、良级供应商配送；每年考评一次，连续三年考评为差级的供应商，原则上进行淘汰。对于供应商企业而言，该组合评价模型不仅能评定出供应商属于哪个等级，还能得到属于各个等级的不同概率值，当属于某两个等级的概率值比较接近时，就需警惕下次进行评价时是否有可能划分到较低的等级并采取相应的措施等。

3　结 语

在当今全球竞争激烈、产品需求日新月异的市场环境下，主导企业为了实现高质量、低成本、快反应、强发展的目标，除了加强自身的综合能力外，还必须站在可持续发展角度上寻求长期战略协作伙伴来提升自身的市场竞争力和地位。因此，如何客观并精确地综合评价、选择供应商是主导企业必须解决的一个重要问题。目前，供应商评价模型众多，但有些模型的单独使用会有一些严苛的前提条件或存在的瑕疵。本文提出了基于层次分析的有序多分类Logistic组合评价模型，综合地、较全面考虑了医药企业供应商定量和定性的4个制约主要素及其子因素，并给出了该模型的具体应用过程。该模型及其应用过程可用于从不同要素上比较系统、全面地评价医药供应商的整体水平，适用于主导企业的供应商选择及管理，为主导企业寻求长期战略协作伙伴及制订药品采购计划提供了一种具有一定理论和应用价值的方法。

主要参考文献

［1］邢鑫鑫.突发事件铁路应急预案组合评价方法研究［D］.兰州：兰州交通大学，2012.

［2］王奇娟，唐晓青，郑联语.基于层次分析法的供应商评价模型［J］.航空制造技术，2008（2）.

［3］许树柏.实用决策方法：层次分析原理［M］.天津：天津大学出版社，1988.

［4］彭建刚，屠海波，何婧，等.有序多分类Logistic模型在违约概率测算中的应用［J］.财经理论与实践，2009（4）.

［5］［美］Robert I Kabacoff.R语言实战［M］.高涛，等，译.北京：人民邮电出版社，2013.

［6］张文彤.SPSS统计分析高级教程［M］.北京：高等教育出版社，2004.

［7］樊震林，黎爱军，等.医疗风险影响因素的有序多分类Logistic回归分析［J］.中国卫生质量管理，2009（4）.

10.3969/j.issn.1673 - 0194.2016.16.041

F274

A

1673-0194（2016）16-0062-03

2016-07-02

国家自然科学基金项目（11271140）。