MIMO系统中改进的LLL格基约减算法

周　围，张　茜，王新贺

(重庆邮电大学 a.移动通信技术重庆市重点实验室；b.光电工程学院，重庆 400065)



MIMO系统中改进的LLL格基约减算法

周围a，b，张茜a，王新贺a

(重庆邮电大学a.移动通信技术重庆市重点实验室；b.光电工程学院，重庆 400065)

针对传统LLL格基约减算法在MIMO系统中的误比特性能较差的问题，提出了一种改进的LLL检测算法。该算法利用后向LLL约减算法和同时对多个初始基进行约减的思想，从问题的多组初始基开始搜索，并对多组初始基进行约减，找到其中最好的一组基，摆脱了传统格基约减算法仅从单组基开始搜索的局限。通过理论分析和计算机仿真，对算法的收敛性及不同收发天线数下不同检测算法的误比特性能进行了对比研究。结果表明，在MIMO系统中本文算法的检测性能比传统的格基约减算法更优，且更接近于ML检测算法。

多输入多输出；格基约减；LLL算法；后向LLL算法

随着社会的发展，现有移动通信系统的业务越来越不能满足人们的要求，因此对系统业务的要求也越来越高，全球无线通信进入高速发展阶段。而多输入多输出(Multiple-InputMultiple-Output，MIMO)技术通过在收发双端同时配置多根天线，充分利用空间资源，在空间产生多个独立的并行信道，从而将多路数据流同时进行传输，因此MIMO无线系统能够在成倍提高系统容量的同时提高频谱资源的利用率，是无线领域关键技术的一个重大突破，吸引了通信领域学术界广大学者的研究兴趣。

目前学术界广泛研究的MIMO系统信号检测算法大致分为非线性与线性两类。非线性检测算法主要有最大似然检测(MaximumLikelihood，ML),球形检测(SphereDetection，SD),K-best,QRDM以及智能检测算法等[1]；线性检测算法主要有ZF、MMSE和半定松弛检测算法。与线性检测方法相比较，非线性检测方法具有优良的检测性能，同时其计算复杂度也比较高，因此难以应用到实际的工程环境中。MIMO系统信号检测算法的性能和复杂度之间呈现一定的正相关关系，但对某一待检测信号进行一定的预处理后，以增加一定的计算复杂度为代价，达到提升系统能检测效果的目的。格基约减作为一种信号检测前的预处理方法，以增加一定的复杂度，能够提升系统的检测性能。因此，将格基约减理论应用到MIMO系统信号检测中可以获得更优的检测效果。文献[2-5]中提及了几种比较经典的格基约减检测算法，主要有LLL算法、HKZ算法和Gauss算法。而在各种格基约减方法当中，LLL格基约减算法因能在性能和复度之间得到很好的折衷而被广泛使用[6-9]，同时也是本文研究的重点。基于LLL的格基约减算法作为一种比较成熟的格基约减技术，不仅能够直接对复数域矩阵进行处理[10]，还能够通过长度规约和列交换操作获得接近正交的约减基，且复杂度较低为多项式时间复杂度。但也存在这样一个问题，随着MIMO系统收发天线数的增加，LLL检测算法的性能也会随之变差，传统的LLL检测算法在MIMO系统中已失效[11]。文献[12-13]中提出一种联合前向后向的LLL格基约减算法，在一定程度上可以改善格基约减在MIMO系统中的性能；文献[14]中提出一种迭代LLL检测算法，该方法在迭代次数较多的情况下可以改善检测算法性能，但是其收敛速度过慢，需进行多次迭代；文献[15-16]中提出一种基于遗传算法的信道矩阵优化，但是在初始种群的选取时复杂度较高，并且对随后的检测带来的利益过小，对子代进行遗传算子操作时其交叉过程会使得约减基维数加倍，对于信号检测而言难以恢复出发送端信号。因此，本文利用前向后向LLL约减联合算法的思想对MIMO系统的信号进行检测，提出一种改进的LLL检测算法。在前向后向LLL约减基的基础上对多个初始基进行LLL约减，进而搜索出一组具有更短长度、更小正交缺陷度的约减基，构成优化矩阵H′，并在该优化矩阵H′下进行信号检测，继而达到改善MIMO系统检测性能的目的。

1　系统模型

在一个发射天线数为Nt，接收天线数Nr的MIMO系统中，接收端模型如式(1)所示

y=Hx+n

(1)

图1　MIMO系统框图

2　格基约减

格的多样性表明一个格可以由多个不同的基来表示，而在信号检测中，则希望能够找到众多基中最短的一组基，以有利于系统接收端信号的恢复。而选择这样一组基的过程称为格基约减，且称这组基为格的一组约减基。在MIMO系统中，格基约减操作的基本原理如式(2)所示

H′=HT

(2)

这里矩阵T为幺模矩阵，由式(2)可知格基约减就是利用幺模变换矩阵将H约减为一个新的、更正交的矩阵H′的过程。根据矩阵的右乘性质可知，矩阵H与幺模矩阵T相乘可以理解为对H的列进行变换，即格基约减就是通过对信道矩阵进行列初等变换，继而获得更优的等效矩阵的过程。

格基约减操作的关键就是如何寻找到最优的等效矩阵H′，本文在传统LLL格基约减算法的基础上引入多个初始基，同时对多个初始基进行格基约减，求解出正交性更好的一组等效约减基H′，从而能够进一步提升系统的检测性能。

A. K. Lenstra， H. W. Lenstra 和L. Lovasz在文献[17]中给出一种可以直接应用于任意维MIMO系统的LLL格基约减算法，该算法与其他格基约减算法相比具有更大的灵活性，且复杂度较低。在MIMO系统中，对Nt维的信道矩阵H进行LLL约减，等效为对H进行QR分解，分解为酉矩阵Q和上三角矩阵R相乘的形式：H=QR，并使矩阵R中的元素满足式(3)和式(4)所示的两个约束条件

(3)

(4)

l=2,…,Nt(1/4<δ≤1)

(5)

(6)

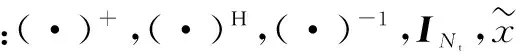
(7)

(8)

式中：Q(·)表示对(·)进行量化处理，通过式(7)、(8)可以恢复出对原始发射信号的估计值

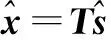
(9)

3　改进LLL算法

传统LLL格基约减算法中，第m(m=1,2,…,Nt)根发射天线的发射符号误码率sm随着下标m逐渐减小,其误码率sm逐渐增大。这意味着第一根发射天线的误码率最大，而第Nt根天线的误码率最小。这是由于LLL算法的整数格点特性，在发射端需要对发射符号x进行格点映射；在接收端经量化判决后，还需经过相应的逆映射过程以恢复原始的发射信号，正是在逆映射恢复原始发射符号的过程中，会左乘一个上三角矩阵，而使得前几根发射天线受到来自其他天线上发射符号的干扰，导致第一根发射天线上发射符号的误码率最大。

传统LLL检测算法是将信道矩阵H的第p列和第q列按一定规则进行迭代列变换(p>q)，而得到新的约减矩阵，这里将传统LLL检测算法进行迭代列变换的操作称为前向约减，称该算法为前向LLL算法；对前向约减的列变换取镜像操作，即将信道矩阵的第p列和q列按一定规则进行列变换(q>p)，得到另一个约减矩阵，将该操作称为后向约减，该算法称为后向LLL算法。

由于采用前向和后向LLL算法之后的信道矩阵相关性较弱，因此能够获得更好的误码率性能，即更可靠的发射符号估计，但仍与最大似然检测差距较大。因此本文引入一种信道矩阵优化技术，将初始信道矩阵与初等变换矩阵相乘，得到多个初始基，对多个初始基进行LLL约减，就会生成多个性能上存在差别的约减基，选取其中最优的一个作为最终输出解。生成初等变换矩阵的具体步骤如下：对经过前向后向LLL算法产生的上三角幺模矩阵和下三角幺模矩阵进行矩阵相乘操作，并对相乘后的矩阵进行随机初等变换，即可生成初等变换矩阵。

改进LLL算法：

1)将输入的初始信道矩阵H分别与M个初等变换矩阵相乘，可产生M组基；

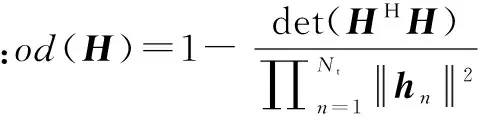
3)将M组新基按正交缺陷度从高到低进行排序；

4)根据正交缺陷度值的大小，按正交缺陷的选取最优即正交缺陷度最小的一组约减基作为输出。

后向LLL算法具体步骤(伪代码)：

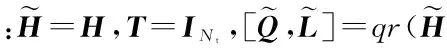
2)令p=Nt-1；

3)whilep≥1；

4)forq=p+1,p+2,…,Nt,do；

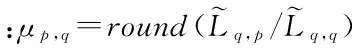
6)ifμp,q≠0，then；

7)更新下三角矩阵和幺模矩阵：

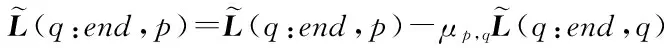
T(:,p)=T(:,p)-μp,qT(:,q)；

8)end if；

9)end；

11)p=p-1；

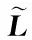
14)p=min{p+1,Nt-1}；

15)else；

16)ifp=Nt-1；

17)end；

18)end；

19)end。

4　仿真结果及分析

图2所示为性噪比SNR=22 dB的情况下，收发天线数为8的MIMO系统中，各天线的BER性能仿真曲线图。其中，LLL曲线表明采用的格基约减方法为传统LLL检测算法，BLLL表示采用的格基约减方法为后向LLL检测算法，FBLLL表示采用的格基约减方法为联合前向后向LLL检测算法。从图中可以看出，传统LLL检测算法，第m(m=1,2,…,Nt)根发射天线的发射符号误码率sm随着下标m逐渐减小其逐渐增大，后向LLL则呈现相反的变化趋势，而前向后向LLL联合检测算法因其较弱的相关性而呈现出各根天线BER性能一致的趋势。证明了联合前向后向LLL检测算法能有效地降低各根天线之间的相关性，得到更优的检测性能。

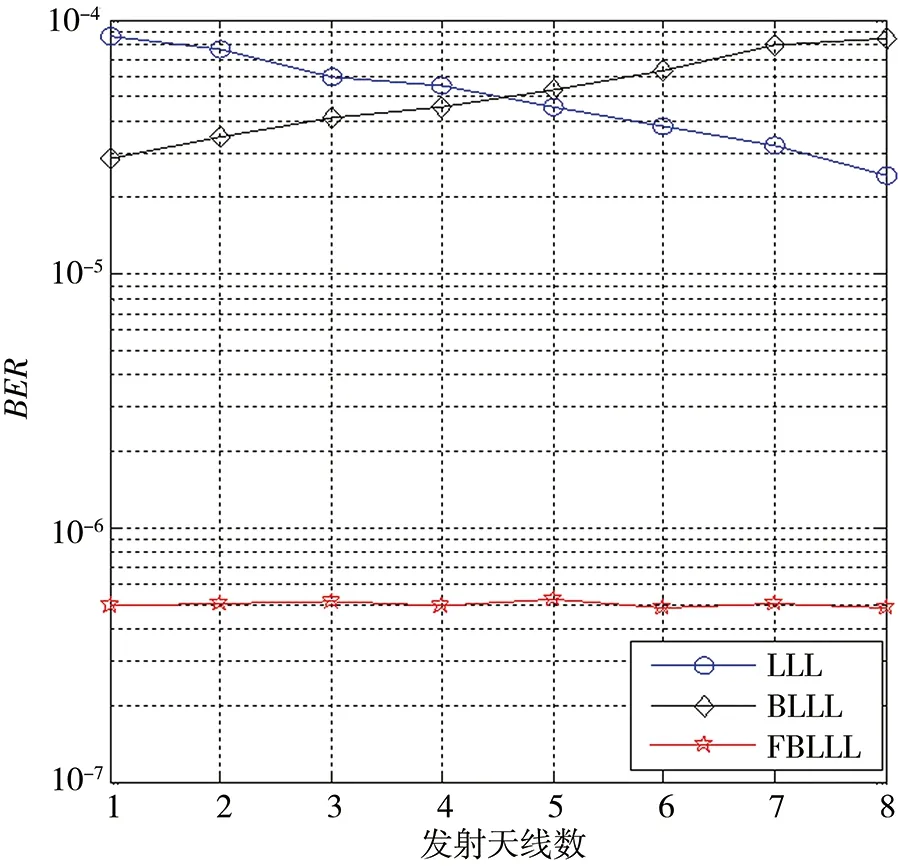
图2　8×8 MIMO系统下各发射天线的误码率率曲线

图3所示为各检测算法在收发天线数为4的MIMO系统中的误码率性曲线图。可以看出，传统的LLL检测算法能够显著地提升线性检测算法的检测性能；而本文算法在BER=10-3时性能相对于传统的LLL线性检测算法只有约1 dB的性能改善。其原因是在4×4 MIMO中，系统规模较小，传统的LLL检测算法能够找到一个足够短的新基来提高检测算法的性能。因此，在收发天线数较小的MIMO系统中，可直接采用传统LLL检测算法来提高检测算法的性能。

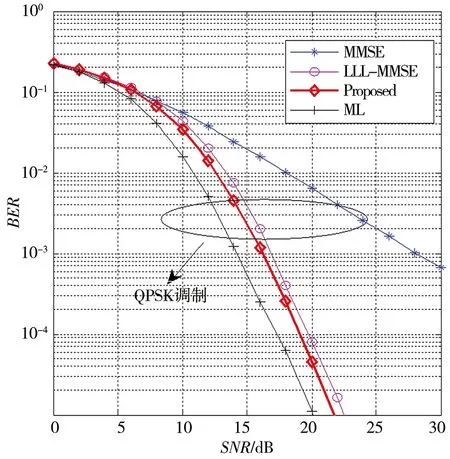
图3　4×4 MIMO下不同检测算法的误比特率曲线

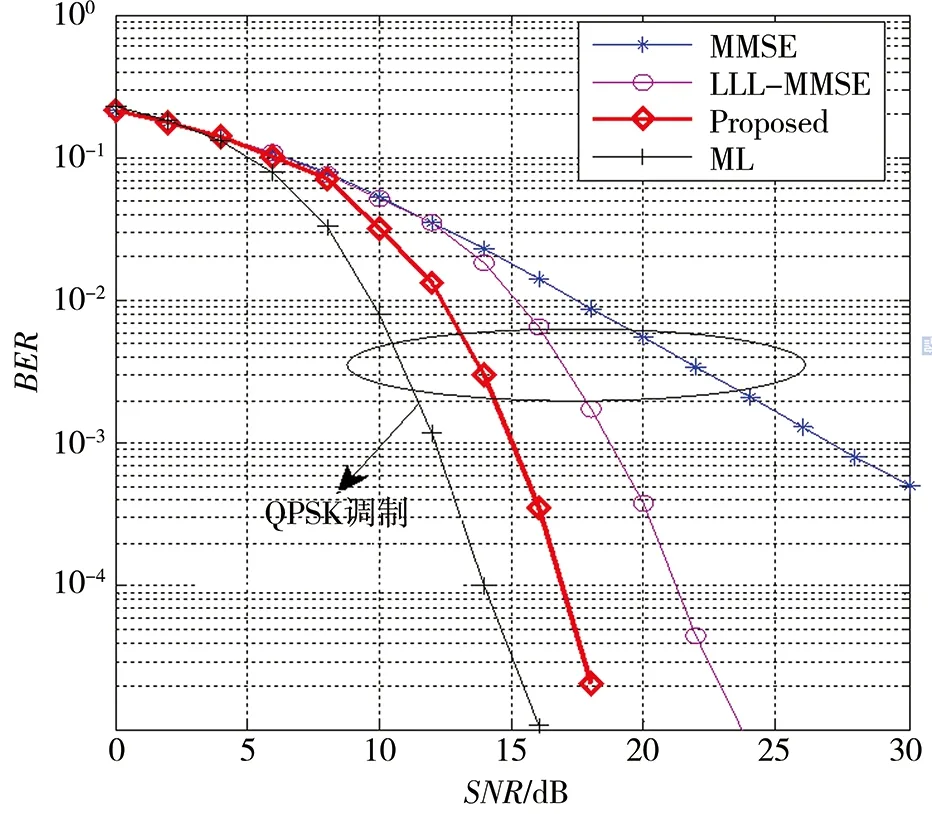
图4　8×8 MIMO下不同检测算法的误比特率曲线

图4所示为8×8 MIMO系统下，各检测算法的BER性能曲线，在BER=10-3时，基于LLL的检测算法相对于线性算法有约7 dB的性能改善；但仍与ML检测存在较大的差距，而改进的LLL检测算法相对于传统LLL检测算法大约有4 dB的性能改善，这样大大缩短了LLL检测算法与ML检测算法之间的差距。原因在于初等变换矩阵的选取时，初等变换矩阵由传统LLL检测算法和后向LLL检测算法生成的上三角和下三角矩阵变化而得，其相关性较小，而后利用初等变换矩阵生成的多个初始基也到达了对信道矩阵进行充分置乱的效果。因此对于生成的多个初始基而言，经LLL约减操作之后能够获得正交性更好、长度更短的等效输出基。使得本文算法的BER曲线更接近于ML检测的BER曲线。

参照文献[19]中提及的格基约减复杂度计算方法，若a取格基中向量长度的最大值，那么LLL格基约减算法的时间复杂度为o(n4lba)；对于一个n×n维的矩阵采用标准的矩阵乘法，其复杂度为o(n3)。假设初始格基的个数为m，那么采用基于本文改进LLL检测算法的整体时间开销为o(n3)+o((m+2)n4lba)。其中主要的时间开销花费在对每组候选初始基进行LLL约减操作上。上述仿真条件中，设定的初始基的数量为4，因此本文的改进LLL约减算法的时间复杂度约为传统LLL约减的6倍。

5　总结

本文提出一种在MIMO系统和MIMO系统下的改进LLL信号检测算法，并且仿真分析表明，在收发天线数为8的MIMO系统中，本文算法能够获得更好的BER检测性能，且更接近ML检测。而在收发天线数为4的MIMO系统中，改进的LLL检测算法相对于传统的LLL检测算法而言，其性能改善得并不明显。因此，本文所提出的改进LLL检测算法更加适用于较大规模的MIMO系统。本文算法以牺牲一定的复杂度为代价，显著地改善了检测算法的性能，使之更接近于ML检测。

[1]吴军， 王绍伟. 改进的K-Best检测算法研究及实现[J]. 电视技术，2013，37(5)：146-149.

[2]WUBBEN D， SEETHALER S， JOAKIM J， et al. Lattice reduction[J]. IEEE transactions on signal processing，2011，28(3)：70-91. DOI：10.1109/MSP.2010.938758.

[3]MUSSI A M， ABRAO T. SDR lattice reduction aided detector[J]. IEEE transactions on latin America，2013，4(11)：1007-1014. DOI： 10.1109/TLA.2013.6601743.

[4]ZHOU Q， MA X L. An improved LR-aided K-best algorithm for MIMO detection[C]// Proc. Wireless Communications and Signal Processing. Huangshan：IEEE，2012：1-5.DOI： 10.1109/WCSP.2012.6542840.

[5]NAJAFI H， DAMEN M O. Lattice reduction aided conditional detection for MIMO systems[J]. IEEE transactions on communications，2014， 62(11)：3864-3873.DOI： 10.1109/TCOMM.2014.2361337.

[6]GESTNER B，MA X L， ANDERSON D V. Incremental lattice reduction： motivation， theory， and practical implementation[J]. IEEE transactions on wireless communications，2012，11(1)：188-198. DOI：10.1109/TWC.2011.120511.102286.

[7]SAKZAD A， HARSHAN J， VITRBO E. Integer-forcing MIMO linear receivers based on lattice reduction[J]. IEEE transactions on wireless communications， 2013， 12(10)：4905-4915. DOI： 10.1109/TWC.2013.090513.121465.

[8]YANG P，XIAO Y，LI S Q， et al. QRD-assisted adaptive modulation-aided MIMO systems[J]. IEEE transactions on vehicular technology，2014，63(1)：446-451. DOI： 10.1109/TVT.2013.2274482.

[9]ZHANG W，QIAO S Z，WEI Y M. A diagonal lattice reduction algorithm for MIMO detection[J]. IEEE transactions on signal processing letters， 2012，19(5)：311-314.DOI： 10.1109/LSP.2012.2191614.

[10]WEN Q S， ZHOU Q， MA X l. An enhanced fixed-complexity LLL algorithm for MIMO detection[C]// Proc. Global Communications Conference. Austin， TX：IEEE，2014：3231-3236. DOI： 10.1109/GLOCOM.2014.7037304.

[11]FUJINO T， SHIMOKAWA T. Combined forward and backward lattice reduction aided MMSE detection in MIMO systems[C]// Proc.Vehicular Technology Conference. Calgary， BC：IEEE，2008：1-6.DOI： 10.1109/VETECF.2008.283.

[12]FUJINO T， SHIMOKAWA T， TRAN X N. A combined forward and backward lattice-reduction aided MMSE list detection[C]// Proc.Advanced Technologies for Communications. Hanoi：IEEE，2008：39-44. DOI： 10.1109/ATC.2008.4760514.

[13]NEGISHI H， WEI H， FUJINO T. MMSE detector using forward and backward reciprocal lattice reduction in MIMO systems[C]// Proc. Signal Processing and Information Technology. Luxor：IEEE，2010：288-292. DOI： 10.1109/ISSPIT.2010.5711796.

[14]HUNUKUMBURE M， SARPERI L. An efficient feed-forward method for lattice reduction MIMO schemes[C]//Proc.22ndInternational Symposium on Personal Indoor and Mobile Radio Communications. Toronto：IEEE，2011：1485-1489. DOI： 10.1109/PIMRC.2011.6139750.

[15]刘金铸， 万翔. 基于遗传算法的无线信道矩阵优化技术[J]. 计算机仿真，2015，32(1)：224-228.

[16]刘向辉，韩文报，权建校. 基于遗传策略的格基约化算法[J]. 电子与信息学报，2013，35(8)：1940-1945.

[17]LENSTRA A K， LENSTRA H W， LOVáSZ L. Factoring polynomials with rational coefficients[J]. Mathematische annalen，1982，261(4)：515-534.

[18]张海波，杨祥红，张嵩. Lovasz条件下LLL算法最简复Givens矩阵形式的研究[J]. 海军航空工程学院学报，2012，27(6)：601-604.

[19]ZHANG W，QIAO S Z，WEI Y M，et al. Reduction algorithm for lattice reduction aided MIMO detection[J]. IEEE transactions on signal processing，2012，60(11)：5963-5976. DOI： 10.1109/TSP.2012.2210708.

周围(1971— )，教授，硕士生导师，博士，主要研究方向为无线移动通信技术、通信系统及信号处理、智能天线技术等；

张茜(1991— )，女，硕士生，主研无线移动通信，信号检测；

王新贺(1989— )，硕士生，主研无线移动通信，阵列信号处理。

责任编辑：闫雯雯

ImprovedLLLlatticereductionalgorithminMIMOsystem

ZHOUWeia，b，ZHANGXia，WANGXinhea

(a. Chongqing Key Laboratory of Mobile Communications Technology;b. College of Optoelectronic Engineering，Chongqing University of Posts and Telecommunications，Chongqing 400065，China)

AimingatthisproblemthatthetraditionalLLLlatticereductionalgorithmachievespoorBERperformanceinMIMOsystems，animprovedLLLalgorithmisproposed.UsingtheLLLalgorithmandreducingmultipleoforiginallatticebasesatthesametime，thealgorithmseeksthesolutionoftheproblemfrommultipleoriginallatticebases.Throughthereductionofthemultipleoriginallatticebases，thebestlatticebasecanbefound.TheimprovedalgorithmcanovercomethelimitationofthetraditionalLLLlatticereductionalgorithm，whichseekingfromasingleoriginallatticebase.Throughtheoreticalanalysisandcomputersimulation，theconvergenceofthealgorithmandtheBERperformanceofdifferentalgorithmsunderdifferentnumberoftransmitandreceiveantennasarestudied.ResultsshowthattheproposedalgorithmachievesbetterperformancethanthetraditionalLLLlatticereductionalgorithm，anditsperformanceisclosertothatofMLalgorithminMIMOsystem.

MIMO；latticereduction；LLLalgorithm；backwardLLLalgorithm

TN929.5

ADOI：10.16280/j.videoe.2016.08.018

国家“863”计划项目(2009AA011302)；重庆邮电大学研究生教育创新计划重点项目(Y201019)；重庆市教委科研项目(K1090513)

2015-12-19

文献引用格式：周围，张茜，王新贺.MIMO系统中改进的LLL格基约减算法[J].电视技术，2016，40(8)：93-98.

ZHOUW，ZHANGX，WANGXH.ImprovedLLLlatticereductionalgorithminMIMOsystem[J].Videoengineering，2016，40(8)：93-98.