基于聚类分析的电缆接线优化设计

席永胜，王丽坤，魏生香

基于聚类分析的电缆接线优化设计

席永胜，王丽坤，魏生香

（兰州寰球工程公司自控室，甘肃兰州 730060）

在石油化工行业的自控工程设计中，使用现场仪表接线箱可以有效减少电缆材料及施工费用，然而实际项目中接线箱的设置一般都是根据主观经验，缺乏科学指导的依据。本文提出一种基于聚类分析的设计方法，从最优化电缆敷设长度的角度出发，进行接线箱数量、位置及电缆分配的优化设计，工程实例验证了所提方法的有效性。

检测技术与自动化装置；聚类分析；电缆接线；优化设计

1　聚类分析基本算法

聚类分析是一种无监督的模式识别方法，目的是将同类数据按照某种相似原则进行划分，力求将相似的数据归于同一类。聚类分析已在诸多工程领域得到广泛应用。温书亮等［1］、邬冬茹等［2］、吕红华等［3］使用聚类分析进行储层的研究，用于油田开发的预测、分析及评价。李燕京等［4］结合图论以及聚类分析中的算法编制了测压点优化选点程序，对长江下游某市供水管网测压点进行优化布置，以确定最优数目和位置的监测点。从优化电缆使用量及确定接线箱布置的角度出发，通过聚类分析研究接线箱及电缆敷设的优化设计方法。

常用的聚类方法有划分法和层次法。层次法不但可以将数据进行类的划分，还可以给决策者提供更为详细的类间所属关系及距离信息，决策者可以根据谱系图对聚类的结果进行进一步的分析。

聚类是一个将数据按照相似性集中的过程，衡量相似性的工具为距离。样品间距离的计算方法有绝对值距离 （Blockdistance）、欧氏距离（Euclidean distance）、闵氏距离（Minkowskidistance）、切比雪夫距离 （Chebychevdistance）、马氏距离（Mahalanobis distance）等。本文所计算距离为三维空间距离，因而选用欧氏距离最为理想。

记X与Y为两个类，Xi与Yi分别是X与Y中的样品。对于X中的两个样品：

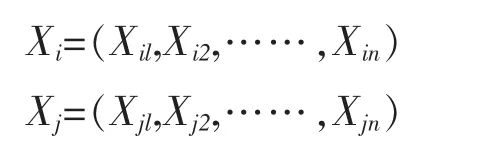
Xi=Yi与之间的欧氏距离为：

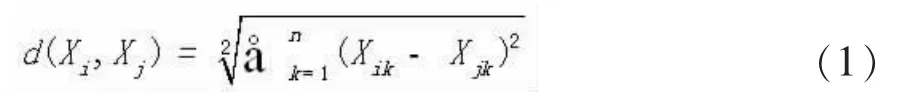
样品经相似性聚集为类，类的进一步聚集同样依据距离。类与类之间的距离有最短距离法（singlelinkage） 、最长距离法（completelinkage）、中间距离法（medianmethod）、类平均法（average linkage）、组平均连接法（Averagegrouplinkage）、可变类平均法（flexible-betamethod）、重心法（centroid method）、Ward离差平方和法 （Ward'sminimumvariancemethod）等，胡雷芳［5］对最短距离法、最长距离法、类平均法、组平均连接法、Ward离差平方和法五中算法从单调性、扭曲性、空间收缩与扩张性及最优性的角度进行了比较与分析，给出了计算类之间距离的建议。重心法使用各类重心的欧式距离表示类与类之间的距离，而重心描述所有样品的均值，因而本文计算类与类之间距离时选用重心法。

1.因变量。农村化学品企业产值(Outputjt)，其中，j和t分别代表省份和年度。本文以《规划》中明确规定的化学品污染重点防控产业中农村化学品企业总产值作为因变量的替代变量。

记

X为类X的重心，Y为类Y的重心，X、Y中分别有［p、q个样品，有：

则类X与Y之间的距离：

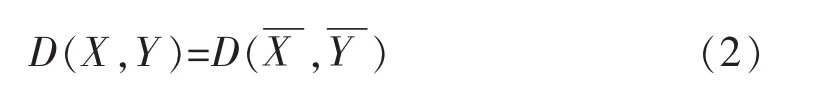
层次划分法聚类的过程为，开始将每个单独样品作为一个类，选择距离最近的两个类，将其合并为一个新的类，重新计算各类之间的距离并再次合并，直至所有类被归为一个类为止。

2聚类分析基本算法

同类信号的分支仪表电缆，从现场仪表接至接线箱，不同信号类型的电缆将按照隔爆、本安、通讯、电源等接入不同的接线箱，因此对分支仪表电缆的聚类，本质上为对同类信号仪表坐标的聚类。对于本文接线箱及电缆敷设优化问题，由于起先并不知道需要聚类的数量（即接线箱的数量），而且每个类中元素的个数有限（每个接线箱能接入电缆的数量有限），因此本文使用层次法进行仪表坐标位置的聚类划分，每个仪表的坐标可由三维辅助设计软件PDMS的QuickReport功能导出。

接线箱一般接入电缆的数量有8、12、16等，实际项目中每个接线箱需要预留不少于10%的备用，因此上述规格接线箱建议最多接入7、11、14根仪表电缆。接线箱个数未知，每根电缆与接线箱之间所属关系未知，接线箱的布置未知。对于上述问题，本文提出一种基于聚类分析进行电缆接线的优化设计方法，确定电缆与接线箱的分配、接线箱的数量、接线箱的位置。过程如下：

1）设共有n根仪表电缆，第根仪表电缆的起始点坐标（既仪表坐标）为xi=（xi1,xi2,xi3,i=1）n，2，3，…，n。每个仪表坐标被划分为一个独立的类，任意两个仪表Xi与Xi坐标间的欧氏距离为：

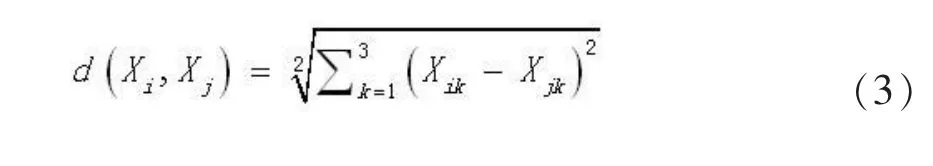
2）根据计算的距离，建立距离矩阵：其中 dij表示类 Xi=（xi1，xi1，xi3）与 Xj=（xj1，xj1，xj3）之间的距离。

3）找出距离最近的两个类Xi与Xj，将其合并为一个新的Xs类，计算每个新类的重心：其中p是当前类中的样品个数。

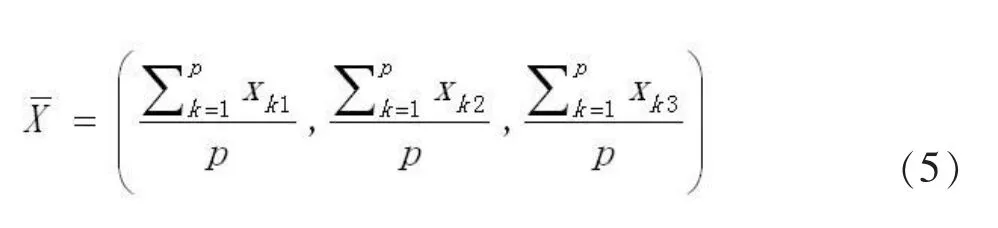
4）计算类与类之间的距离，本文使用重心法，既：

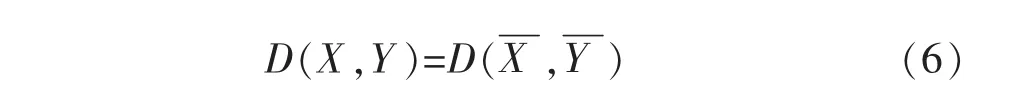
据此得到新的距离矩阵。

5）重复步骤2）～4），直至所有类被合并为一个类，结束聚类过程。

6）建立谱系图。

根据聚类结果建立谱系图，按照接线箱所能容纳的电缆数量进行电缆与接线箱之间的分配，一个类中距离最近的仪表电缆将被分配至同一接线箱，超过接线箱最大容量的电缆，则被分配至下一接线箱。

7）计算最终每个类的重心，以重心为原点，就近设置接线箱的位置。由于接线箱的位置设置要考虑设备布置、人员走道、检修通道等现场实际情况，一般情况下宜就近安装在钢支柱等位置。接线箱距离对应重心位置越近，分支电缆越短。

由于不同信号接入不同的接线箱，因此不同信号电缆的分配互不影响，对不同信号电缆的分配只需独立重复上述过程即可。

基于上述算法，使用VB语言开发出一个简单的应用软件，将PDMS导出的仪表坐标文件导入该软件，对信号进行分类，输入接线箱的规格、类型及允许布置接线箱的位置，软件会自动将分支电缆进行分配，并给出最佳的接线箱布置位置，同时计算出每根电缆至对应接线箱的长度及所有分支电缆的总长度，如果设计者对结果不满意，可以人为进行适当调整，软件将动态计算调整后电缆的重新分配及电缆长度。

3　工程实例

以下实例源于某碳四深加工项目，为使计算简单且具有代表性，仅选取项目中部分数据。仪表电缆均为本安型，接线箱可接入8芯电缆。现场仪表共40个，为展示直观，选择同一平面内仪表，因此坐标为二位向量，仪表位置如图1所示。

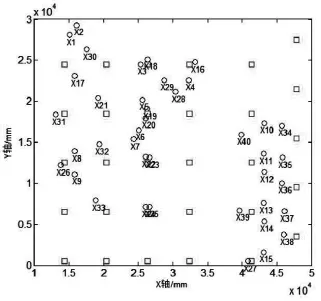
图1　仪表及钢支柱位置分布

其中“○”表示仪表位置，下方数字为仪表编号（仪表所对应电缆编号），“□”表示钢支柱的位置，钢支柱上可布置接线箱。

由于本实例数据量较大，起始距离矩阵为50× 50，因此文中省略中间聚类过程，只给出最终聚类的谱系图，如图2所示。

根据本文所提优化设计方法，仪表分支电缆与接线箱之间的分配结果见表1。

表1　仪表分支电缆与接线箱间的分配

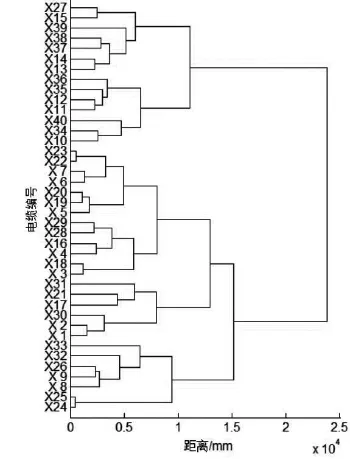
图2　仪表位置聚类谱系图

最后，计算每个类的重心坐标，结合现场钢支柱的位置选择接线箱的安装位置，如图3所示。

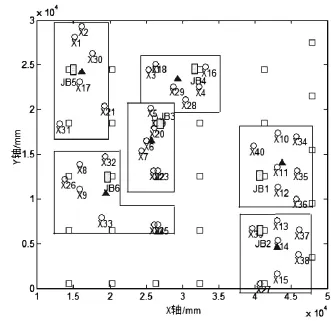
图3　电缆分配划分及接线箱位置分布

其中“△”表示每个类的重心，以重心为圆点就近在钢支柱上布置接线箱，如图3，长方形框表示接线箱的位置，可以看出，相近位置的仪表被接至最近的接线箱。

图4　VB程序电缆分配界面

本实例VB程序运行的结果见图4，可显示每个接线箱的规格、分支电缆分配情况、接线箱坐标及分支电缆的长度。

事实表明，与传统设计方法相比，在某烷基项目中通过使用本文所提设计方法，分支电缆至少减少20%的使用量，从而有效降低工程费用。

4　结论与展望

基于聚类分析，结合自控工程设计实际，提出了一种分支电缆与接线箱的分配及接线箱布置的最优设计方法，帮助设计者进行分支电缆分配及接线箱分布的设计，优化了电缆敷设路径，有效提高了设计质量与效率，减少了施工成本，从而降低项目投资。值得指出，在自控工程设计中，除仪表电缆敷设中可以使用聚类分析进行辅助设计，仪表供气、伴热、供电点的选择也可使用本文所提的优化设计方法。

［1］ 温书亮，刘志斌，何峰.地震多属性聚类分析技术及其在渤海某区块油气预测中的应用［J］.天然气工业，2007，S1：373-374.

［2］ 邬冬茹，朱忠宽.聚类分析在储层微相分析中的应用［J］.汉江石油学院学报，2003，25（z2）：26-26.

［3］ 吕红华，任明达，柳金诚，等.Q型主因子分析与聚类分析在柴达木盆地花土沟油田新近系砂岩储层评价中的应用［J］.北京大学学报（自然科学版），2006，42（6）：740-745.

［4］ 李燕京，吕谋，司鹏敏.给定测点数的管网测压点优化布置方法［J］.供水技术，2009，3（5）：43-46.

［5］ 胡雷芳.五种常用系统聚类分析方法及其比较［J］.浙江统计，2007（4）：11-13.

TP21