水下机器人抗波浪扰动动力定位研究

刘慧婷，张　明，曾庆军，眭　翔，宋振文

(1.江苏科技大学 电子信息学院，江苏 镇江　212003; 2.常州信息职业技术学院机电工程学院，江苏 常州　213164；3.江苏科技大学 计算机科学与工程学院，江苏 镇江　212003)



水下机器人抗波浪扰动动力定位研究

刘慧婷1，张明1，曾庆军1，眭翔2，宋振文3

(1.江苏科技大学 电子信息学院，江苏 镇江212003; 2.常州信息职业技术学院机电工程学院，江苏 常州213164；3.江苏科技大学 计算机科学与工程学院，江苏 镇江212003)

针对水下机器人近水面运动受到波浪干扰而产生的不确定性问题，结合所研制的新型海洋工程模态切换机器人MC-ROV，文章基于CFD法建立动力学模型，进行6DOF动力定位分析；根据定位误差设计力和力矩分配策略，采用非奇异终端滑膜控制(NTSM)对推力予以补偿，以减小由波浪等随机带来的影响，并采用无味卡尔曼(UKF)实时估计水下机器人的状态；仿真结果表明，该方法具有良好的动力定位效果，并且在受扰动后可以迅速调整动力分配策略，减小其带来的负面影响。

水下机器人；动力定位；扰动；非奇异终端滑动模型；无味卡尔曼

0　引言

水下机器人被用于各种水下作业，在探索、检修、监控等方面发挥极为重要的作用。水下机器人动力定位是利用一系列使动装置(主要为推进器)使其保持在某一特定位置和角度。动力定位系统由传感器、控制器、滤波算法和推进器等组成，不仅要克服系统本身的高度非线性和耦合性，还要注意外部干扰如波浪、海流等[1]。由于水下机器人的动态行为在很大程度上决定于推力的大小和方向，因此对推进器实施恰当的控制策略十分重要。

目前，已有众多的学者研究水下机器人动力定位方法，取得了丰硕成果。一直以来，扩展卡尔曼(extended kalman filter，EKF)和PID常被用于动力定位控制，Balchen与Grimble等人都曾提出相关的改进算法并获得良好效果[2]。然而其缺陷在于增益调节较难，无法灵活的适应环境变化，而且鲁棒性难以得到保障。2001年，Tannuri Donha和Pesce应用滑动模型控制(sliding mode control，SMC)理论进行动力定位研究，并证明其可行性和鲁棒性[3]。文献[4]提出一种滑模控制方法，验证与PID相比，其对与多数环境具有良好的特性和稳定性。文献[5]基于一种异步数据算法设计了扩展卡尔曼滤波器，使水下机器人定位误差减小20%。文献[6]介绍了一套包括硬件、软件和算法的水下机器人控制系统，对水下机器人的航向和其他自由度运动分开控制，取得不错的实验效果。文献[7]验证了在有效的动态补偿下，超短基线在水下机器人动力定位中的可行性。文献[8]针对水下机器人推理的动态过程，分析并采用一种模糊滑膜控制方法进行动力补偿，Lyapuno方法证明其可在有限时间内收敛并能保证鲁棒性。其他如模糊控制、神经网络控制及其改进算法等等都已取得不错的成果。

考虑水下机器人水动力特性和环境干扰，本文以自主研制的模态切换水下机器人(Mode-converted ROV，MC-ROV)为对象，建立较为完整的6DOF运动模型，采用终端滑动模型(terminal sliding mode，TSM)、无味卡尔曼(unscented kalman filter，UKF)方法进行动力分配和位置计算，使MC-ROV动态地保持在目标位置。

1　动力学模型

1.1MC-ROV简述

MC-ROV是开架式小型水下机器人，航速3节，重80 kg，具有水中浮游和爬壁两种工作模式，可以根据工作需要进行勘察或清污作业。其模态切换功能依靠一个垂向的吸附推进器和压缩弹簧来实现：吸附推进器为小车轮和清污滚轮提供动力，可以沿壁爬行清污；压缩弹簧解除爬壁模式，此时可以浮游作业。

1.2动力学模型

MC-ROV在水中做6DOF运动，即三轴移动和三轴旋转。为方便计算，水下机器人运动参数定义如表1所示。

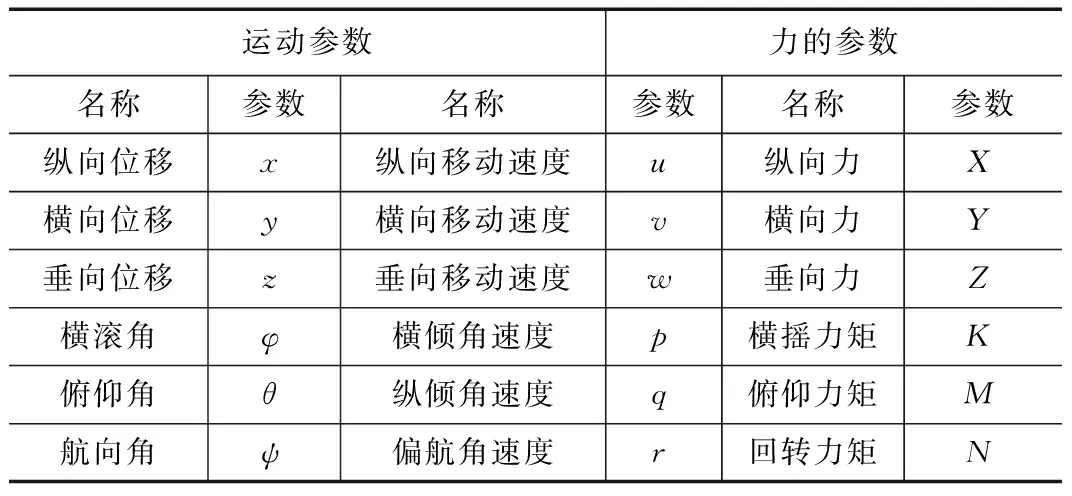
表1　参数定义

在静水中，可用下述方程描述水下机器人动力学特性[9]：

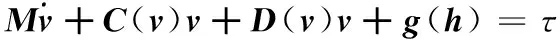
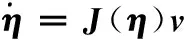
(1)

其中：

η=[xyzφθψ]Τ；

v=[uvwpqr]Τ；

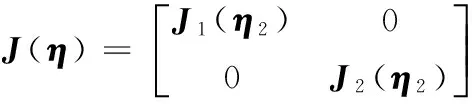
M为水下机器人惯性矩阵，M∈R6×6；

C(v)为水下机器人科氏及向心力矩阵，C(v)∈R6×6；

D(v)是水下机器人流体阻力矩阵，D(v)∈R6×6；

g(η)是由重力和浮力组成的回复力矩阵，g(η)∈R6×1；

τ是水下机器人推进器提供的推力，τ∈R6×1。

而在实际运行时，还要考虑周围环境干扰，如水流、波浪等带来的影响。假设ξd为干扰力，vd表示伴随干扰力产生的速度，则实际动力学模型应调整为[10]

(2)

1.3模型参数

水下机器人动力学模型计算涉及众多的水动力系数，目前主要有3种辨识方法：经验法、试验法和CFD法[11]。由于采用CFD可以方便的在计算机上实现各种流场、速度场等环境下的计算，成本低，速度快，因此这里基于FLUENT软件进行CFD数字模拟辨识参数。水下机器人在水中运动时，主要考虑流体惯性类系数和粘性类系数。其中惯性类水动力系数与加速度线性相关，用附加质量描述，而粘性类水动力系数与速度的一次项和二次项相关。考虑MC-ROV的低速运行、上下对称、开架式结构等，同时选择机体坐标系原点位于重心，浮心与重心基本重合，忽略众多的耦合项和高于三阶的项，可以大大简化水动力模型[12]。

令MC-ROV重心为xG=yG=zG=0，式(a)中惯性矩阵为

M=

(3)

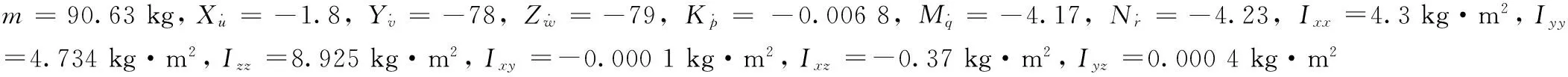
C(v)由科氏向心力矩阵和附加质量矩阵组成，表示为

(4)

式中,

阻尼力D(v)主要由阻力一次项和二次项组成，即

(5)

其中，各自由度二次阻尼系数为：

Xu|u|=-189 N·m-2s2，Yv|v|=-292.98 N·m-2s2，Zw|w|=-314.58 N·m-2s2，

Kp|p|=-46 N·m-2s2，Mq|q|=-76 N·m-2s2，Nr|r|=-38 N·m-2s2。

一次阻力系数为

Xu=-148.18 N·m-2s2，Yv=-785.69 N·m-2s2，Zw=

-414.09 N·m-2s2，

Kp=-79.21 N·m-2s2，Mq=-103.22 N·m-2s2，Nr=-44.41 N·m-2s2。

回复力矩阵g(η)为重力和浮力向量：

(6)

其中：W和B分别为重力和浮力，xB、yB和zB为MC-ROV浮心。经过调平衡，MC-ROV的重力最后为W=888.174N，浮力为B=892.878N，重心和浮心之间的关系可描述为xB-xG=0，yB-yG=0，zB-zG=0.154 6 m。

2　定位算法分析

在对水下机器人实时控制时，要求能够及时适应突变的运动环境，即在受到波浪、海流等影响时迅速改变控制量。本文根据定位误差有序地进行初次动力分配，然后利用NTSM对外部干扰和不确定性具有鲁棒性对推力做动态补偿。同时，运用UKF滤波器估计水下机器人实时位置，以进行下次动力分配。

2.1非奇异终端滑模

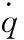
定义运算

(7)

则本算法的NTSM设计如下[14]

(8)

式中，β=diag{β1,···β6}，βi>0，1<γi<2，i=1,2,…,6。

MC-ROV由某一状态趋近qd时按如下规定到达

(9)

其中：k1、k2为常数项，ρi>0，i=1,2,···,6。

对于动力定位系统，控制器终端变量设计为

(10)

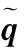
2.2无味卡尔曼

UKF，即无味卡尔曼滤波(unscented kalman filter，UKF)是20世纪90年代出现的一种非线性滤波方法，具有估计精度高、收敛速度快等优点，而且不必对非线性函数求导，在动力定位中具有广泛的应用[15]。UKF的基础是Unscented变换(unscented transformation，UT),其基本思想是用一组确定的离散采样点(即Sigma点)来近似状态变量的分布。UKF假定状态满足高斯分布，因此只需逼近其均值和方差[16]。

MC-ROV水下机器人的控制模型按式(2)进行，控制过程中加入不确定环境干扰。将式(2)整理变换为

(11)

考虑Unscented卡尔曼滤波算法基于如下非线性离散状态空间模型：

(12)

式中，xk=[ηv]Τ，B=[06×6M-1]Τ，u∈R6×1是推进器推力，hk(xk)=Hxk，fk(xk)=[J(η)v-M-1CRBv-M-1CAvξ-M-1Dvξ-M-1g]Τ。

Unscented卡尔曼滤波与基本卡尔曼滤波一样，也是由时间更新和测量更新构成的，

按如下过程进行。

时间更新：

测量更新：

2.3动力分配方法

假设水下机器人的三轴直线运动误差和三轴旋转误差为e=[exeyezeφeθeψ]Τ。针对误差设计推力如下

(13)

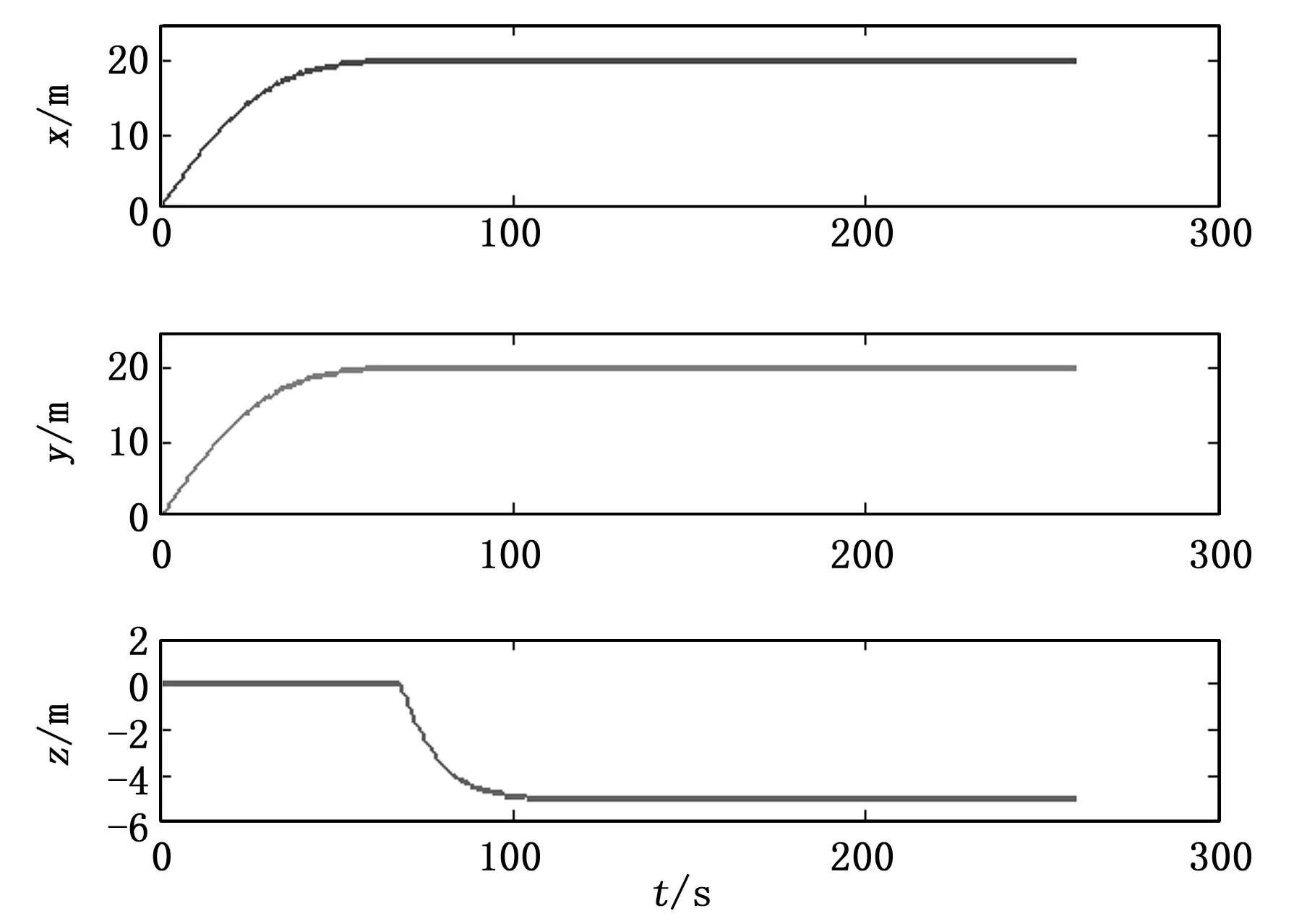
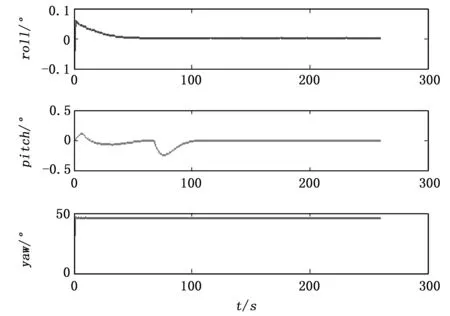
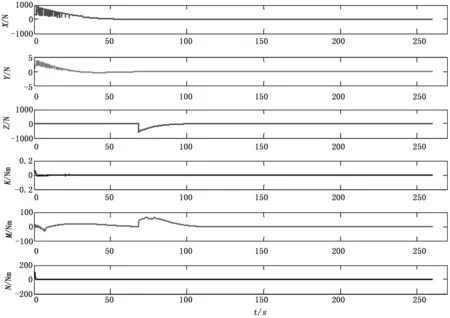
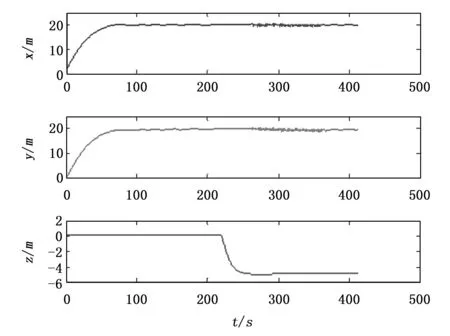
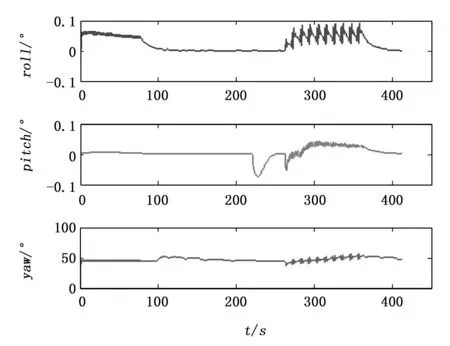
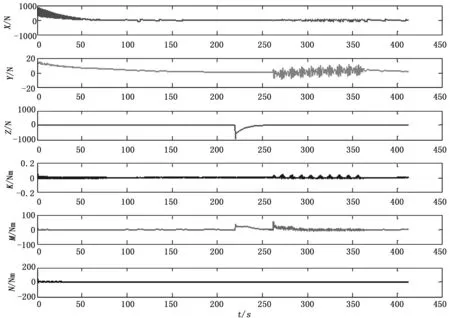
式中，n1、n2为调节因子，Fmax是推进器最大推力，T是单个推进器推力，-Fmax

在6DOF动力定位时，采用有序定位的方法，即按照先定艏向，再定位置，最后定姿态的顺序依次完成整个定位系统。这样可以使动力分配更加条理，避免动力分配混乱的情况。水下机器人MC-ROV的推进器共5个，两个水平推进器和3个垂向推进器。因此，在计算出单个推进器的推力后，需按下式分配推力

(14)

其中，T1、T2、T3、T4、T5分别为5个推进器的推力，a=0.253 m，b=0.341 m。

由NTSM补偿的动力为

(15)

其中:A6×6为可调系数矩阵。

最终的动力分配策略为

(16)

3　算法仿真

水下机器人在近水面航行时，主要受海流(current)和波浪(wave)影响。由于航行速度和时间有限，航行水域也较小，可以近似认为海流不变[17]。而波浪的运动是较为复杂的随机过程，常利用PM谱(pierson-moskowitz spectrum)进行分析、计算波浪运动[18]。

PM谱在实际使用时难以预知，为简便起见，以纵向为例，采用如下方程简单描述波浪运动：

(17)

式中，ai表示波浪幅值，ki为波数，ωi、εi为频率和初相。

其在水平和垂直方向上的速度为

(18)

(19)

首先考虑无干扰情况，假设MC-ROV在无限深广的静水中航行，初始位置定义为为原点，目标位置为(x,y,z)=(20,20,-5)。对于TSM，β=0.4、γ=1.4、k1=3、k2=6、ρ=0.9。对于UKF，状态初值x0=012×1，方差初值P0=1 000I12×12，系统噪声和量测噪声分别为

图1～2为静水中动力定位的位置和姿态曲线。图中，x、y、z为纵轴、横轴和垂向上的位移，roll、pitch、yaw为横滚角、俯仰角和航向角。由图可知，水下机器人在静水中基本能够快速、平稳得到达指定位置，只有俯仰角在水下机器人下潜时产生小幅度波动。

图1　位置曲线

图2　姿态曲线

图3为水下机器人推力和力矩变化曲线图。

图3　力和力矩

在同样的条件下，加入两次波浪干扰，一次在定位过程中(25 s

图4　位置曲线(扰动时)

图5　姿态曲线(扰动时)

图6　力和力矩(扰动时)

4　结论

本文基于NTSM和UKF设计了一种水下机器人6DOF动力定位方法，根据定位误差分配推力，运用NTSM方法进行推力补偿，同时不断以UKF实时估计水下机器人的状态。从无干扰和有干扰两种环境下的仿真结果得知，该方法能够快速、有效到达指定位置，具有一定的抗干扰能力。该方法对其他环境干扰如海流等的抵抗能力还需进一步研究。

[1]范士波. 深海作业型 ROV 水动力试验及运动控制技术研究[D]. 上海：上海交通大学, 2013:50.

[2] Balchen J G, Jenssen N A, Salid S. Dynamic positioning using Kalman filtering and optimal control theory[A].IFAC/IFIP symposium on automation in offshore oil field operation[C]. 1976, 183.

[3] Donha D C, Tannuri E A. Non-linear semi-submersible positioning system using an H-infinity controller[A].Proceedings of the control applications in marine systems conference (IFAC-CAMS 2001)[C]. Glasgow, Scotland, CD-ROM. 2001.

[4] Tannuri E A, Agostinho A C, Morishita H M, et al. Dynamic positioning systems: An experimental analysis of sliding mode control[J]. Control engineering practice, 2010, 18(10): 1121-1132.

[5] Steinke D M, Buckham B J. A kalman filter for the navigation of remotely operated vehicles[C].OCEANS, 2005. Proceedings of MTS/IEEE. IEEE, 2005: 581-588.

[6] Dukan F, Ludvigsen M, Sorensen A J. Dynamic positioning system for a small size ROV with experimental results[A].OCEANS, 2011 IEEE-Spain[C]. IEEE, 2011: 1-10.

[7] 邢志伟, 于开洋, 王晓辉. 超短基线定位系统在ROV动力定位中应用的可行性研究[J]. 机器人, 2002, 24(6):487-491.

[8] Bessa W M, Dutra M S, Kreuzer E. Dynamic Positioning of Underwater Robotic Vehicles with Thruster Dynamics Compensation[J]. International Journal of Advanced Robotic Systems, 2013, 10:1-8.

[9] Sorensen A J. A survey of dynamic positioning control systems [J]. Annual reviews in control, 2011, 35(1): 123-136.

[10] Fossen T I. Marine control systems: guidance, navigation and control of ships, rigs and underwater vehicles [M]. Marine Cybernetics, 2002:123-138.

[11] 邓志刚, 朱大奇, 方建安. 水下机器人动力学模型参数辨识方法综述[J]. 上海海事大学学报, 2014, 35(2): 74-80.

[12] Chin C S, Lau M W S, Low E, et al. Software for modelling and simulation of a remotely-operated vehicle (ROV)[J]. Professional Paper 5 (2006), 2006, 3: 114-125.

[13] 袁雷, 肖飞, 沈建清, 等. 基于扰动观测器的不确定非线性系统非奇异终端滑模控制 [J]. 控制与决策, 2014, 29(2): 353-357.

[14] Yu S, Yu X, Shirinzadeh B, et al. Continuous finite-time control for robotic manipulators with terminal sliding mode [J]. Automatica, 2005, 41(11): 1957-1964.

[15] Cadet O. Introduction to Kalman Filter and its use in dynamic positioning systems [A].Proceedings of Dynamic Positioning Conference[C]. 2003: 16-17.

[16] Krishnamurthy P, Khorrami F. A self-aligning underwater navigation system based on fusion of multiple sensors including DVL and IMU [A].Control Conference (ASCC), 2013 9th Asian[C]. IEEE, 2013: 1-6.

[17] 曹永辉. 复杂环境下自主式水下航行器动力定位技术研究[D]. 西安：西北工业大学, 2006.

[18] 孙行衍, 付明玉, 施小成,等. 基于UKF联邦滤波的动力定位船舶运动状态估计[J]. 中国造船, 2013 (1):114-128.

Research on Dynamic Positioning of ROV Anti-waves

Liu Huiting1，Zhang Ming1, Zeng Qingjun1, Sui Xiang2, Song Zhenwen3

(1.School of Electronic and Information，Jiangsu University of Science and Technology, Zhenjiang212003,China;2.School of Mechanical and Electrical Engineering, Changzhou College of Information， Changzhou213164,China;3.School of Computer Science and Engineering, Jiangsu University of Science and Technology, Zhenjiang212003, China)

In terms of the uncertainties induced by wave disturbances when an underwater vehicle is operated by the surface of water and combined with the novelty Model-Converted Remotely Operated Vehicle (MC-ROV) of ocean engineering, a dynamic model based on CFD is built to analyse 6DOF positioning. A strategy of force and moment allocations is designed according to positioning error, then compensating it with an algorithm known as Non-singular Terminal Sliding Model (NTSM) to low the impact brought by waves likewise. Meanwhile Unscented Kalman Filter (UKF) is utilized to estimate the real-time states of the vehicle. Simulation results present that this algorithm makes the underwater vehicle reach a pre-given position rapidly and effectively, and it can adjust the strategy of force and moment promptly when encounters with perturbations so that reduces the negative effects.

remotely operated vehicle; dynamic positioning; disturbance; NTSM; UKF

2015-06-28；

2015-09-06。

国家自然科学基金项目(11204109)；江苏省产学研前瞻性联合研究项目(BY2012181)；江苏科技大学海洋装备研究院2015年科研项目A类。

刘慧婷(1990-)，硕士研究生,主要从事导航定位与水下机器人研究工作。

1671-4598(2016)01-0199-05

10.16526/j.cnki.11-4762/tp.2016.01.055

TP273

A

曾庆军(1969-)，博士，教授,主要从事智能电气与系统与水下机器人研究工作。