控制方向未知的输入受限非线性系统自适应模糊反步控制

王永超, 张胜修, 曹立佳, 扈晓翔

(火箭军工程大学自动控制工程系, 陕西 西安 710025)



控制方向未知的输入受限非线性系统自适应模糊反步控制

王永超, 张胜修, 曹立佳, 扈晓翔

(火箭军工程大学自动控制工程系, 陕西 西安 710025)

针对一类输入受限控制方向未知的非线性系统,提出一种基于Lipschitz条件的自适应模糊反步控制器的设计方法。在控制器的设计过程当中,通过变换系统形式和采用Butterworth低通滤波器解决控制方向未知的问题;采用模糊系统对不确定非线性函数进行在线逼近;利用双曲正切函数和Nussbaum函数对系统输入饱和函数进行处理;将动态面法与反步法相结合解决“计算膨胀”的问题。运用Lyapunov理论分析证明设计的控制律能够使闭环系统所有信号半全局一致有界(semi-globallyuniformlyultimatelybounded,SGUUB)。该方法的有效性在一类通用的高超声速飞行器的攻角控制仿真中得到了验证。

输入受限;非线性系统;自适应模糊;反步法;高超声速飞行器

0　引　言

输入受限问题普遍存在于控制系统工作过程中。近年来,引起了广大学者的普遍关注。基于小波网络,文献[1]设计出了一种抗饱和自适应控制器。文献[2]针对线性自抗扰控制(linearactivedisturbancerejectioncontrol,LADRC)执行机构的饱和约束问题,提出了两种抗饱和补偿方案。文献[3]提出了一种针对控制受限问题的时变滑模控制方案。文献[4]提出了一种利用神经网络在线逼近补偿执行机构的饱和非线性智能自适应滑模控制方法。文献[5-6]利用双曲正切函数解决输入饱和受限问题,引入Nussbaum增益函数应对未知项,基于反步法设计出了鲁棒控制器。文献[7-8]利用线性矩阵不等式(linearmatrixinequation,LMI)设计出了对饱和进行实时补偿的控制器。文献[9-10]将系统输入幅值受限问题转化为预测控制框架中待求解目标函数的约束条件。

1991年,由Kokotovic等人首次提出反步法[11]。反步法实际上是一种由前向后递推的方法,所以又称逐步后推法,在解决具有纯反馈形式的非线性系统控制器设计问题上,具有明显的优势。但是传统的反步法,虚拟控制器需要反复求导,计算量随着阶数的增加呈指数增长,这使得控制器难以工程化实现。为了有效应对这种被Bellman称为“微分爆炸”的难题,文献[12]引入了一阶滤波器,首先提出了称之为动态面控制(dynamicalsurfacecontrol,DSC)的方法,避免了虚拟控制量的反复求导。伴随着模糊理论的发展,自适应模糊反步法已经广泛应用于非线性系统控制器的设计[12-13]。这一类的控制算法具备以下所列出的显著优势:①无需被控系统满足匹配条件;②无需被控系统的未知非线性函数能够参数线性化。故自适应模糊反步法在针对非线性不确定系统控制器设计上应用非常普遍。

近年来针对不满足匹配条件的非线性系统输入受限问题,许多学者将反步法与模糊逼近相结合进行了比较深入的研究[5,14-15]。但这些研究成果在处理控制方向问题上,一般采用假设已知控制方向的做法。控制方向未知的非线性系统控制器设计有待进一步解决。

本文针对一类输入受限的单输入单输出(singleinputsingleoutput,SISO)系统,提出一种基于Lipschitz条件的自适应模糊反步控制方法。在设计虚拟控制律的过程中,通过变换系统形式和采用Butterworth低通滤波器解决控制增益方向未知的问题,运用带有中心平均解模糊器的模糊系统在线逼近系统中包含不确定参数的函数。将双曲正切函数和Nussbaum函数有机结合,应对输入饱和和补偿所引起的未知项。系统的闭环系统稳定性能通过Lyapunov经典稳定理论进行详细地分析证明。

1　问题描述及模糊逻辑系统建立

1.1问题描述

考虑如式(1)所示的一类SISO非线性系统:

(1)

式中,xi(t)=[x1(t),…,xi(t)]T∈Ri是状态向量;y∈R是输出量;fi(·)和gi(·)均为未知的光滑非线性函数;v(t)为系统控制器输入量;d(t)为系统受到的外界干扰;u(v(t))为具有饱和约束性质的输出控制量,其表达式为

(2)

式中,uM是系统式(1)中控制器的输出上界值。

定义双曲正切函数h(v(t))(v(t)记为v,其他变量和状态作类似处理)为

(3)

则饱和函数可以表示为

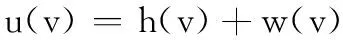
(4)

式中,w(v)=sat(v)-h(v)为有界函数,其界限值表示为

(5)

文中的目的是通过设计鲁棒控制器使得式(1)中的输出y能够稳定跟踪参考指令yr。

根据控制器设计和稳定性证明过程中的实际需求,作出如下合理的假设、定义和引理。

假设 1参考信号yr及其n阶导数已知且有界。

定义 1如果连续函数N(s)满足如下性质:

则称N(s)为Nussbaum函数。

引理 1[15]V(·)和χ(·)均为定义在区间[0,tf)上的光滑函数,且∀t∈[0,tf),V(t)≥0,N(χ)为Nussbaum增益函数。如果如式(6)所示不等式成立,则函数V(·)和χ(·)在[0,tf)必有界。

(6)

式中,C,M,γχ>0均为常数;ζ为一正变量。

1.2模糊逻辑系统建立

模糊器、知识库、模糊推理机和解模糊器构成模糊逻辑函数这个有机整体。依赖于经验知识建立的知识库是模糊系统的核心。知识库包含如下所示的IF-THEN模糊规则:

假设 2[16]文中建立的一系列IF-THEN模糊规则中,模糊集Bl为标准模糊集。

根据假设2,建立的模糊基函数表示为

(7)

(8)

引理 2[17]如果F(x)(x∈Rn)是紧集Ω上的一个连续函数。∀ε>0,必将存在FLS使得

(9)

定义最优估计参数集

(10)

假设 3存在未知有界常数ε*>0,使得模糊逼近误差ε(x)=F(x)-θTξ(x),满足|ε(x)|≤ε*。

2　控制器设计及稳定性分析

根据式(3),系统等效为

(11)

(12)

式中,HL(s)为Butterworth低通滤波器(lowpassfilter,LPF)。

(13)

式中,‖·‖表示向量的2-norm范数。

假设 5[18-20]执行器具有低通特性,即使得xi,f=HL(s)·xi≈xi。故存在一常数βi,0使得不等式|xi-xi,f|≤βi,0成立。

需要说明的是,假设5中xi,f≈xi,uf≈h(v)是合理的,因为大多数控制系统的执行器具有低通特性[18-20]。

下面将结合反步法和DSC开展受限控制器的设计工作。

步骤 1定义

z1=x1-yr

则z1关于时间t的导数为

(14)

(15)

式中,τ1为一阶滤波器的时间常数。

定义

(16)

(17)

根据式(17),κ1关于时间t的导数为

(18)

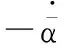
根据式(14)～式(16),z1关于时间t的导数为

(19)

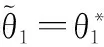
选择Lyapunov函数为

(20)

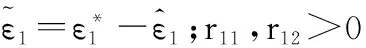
(21)

将式(19)代入式(21),得

(22)

引理 3对于∀D>0,|x|-xtanh(x/D)≤0.278 5D=D′成立。

(23)

(24)

(25)

式中,c1>0为常数。

采用投影法[16],引入参数的自适应律为

(26)

式中,M1为设定的最大值。根据文献[16]可知,估计参数θ1满足‖θ1‖≤M1,并且使得

(27)

则根据式(23)～式(27),式(22)可变换为

(28)

根据Young’s不等式,假设4和假设5可得

(29)

(30)

(31)

则式(28)可变换为

(32)

步骤 i(2≤i≤n-1)定义

(33)

(34)

(35)

(36)

zi关于时间t的导数为

(37)

同时对式(35)求导,得

(38)

选择Lyapunov函数Vi为

(39)

式中,ri1,ri2>0。则Vi关于时间t的导数为

(40)

根据引理3,式(40)可变换为

(41)

选取参数自适应律：

(42)

(43)

(44)

式中,ci>0为常数。

并根据上述参数自适应律和Young’s不等式以及假设4和假设5,式(41)可变换为

(45)

步骤 n定义

(46)

(47)

(48)

(49)

式(46)和式(48)关于时间t的导数分别为

(50)

(51)

选择Lyapunov函数Vn为

(52)

式中,rn1,rn2>0。则Vn关于时间t的导数为

(53)

根据引理3,式(53)可变换为

(54)

选择参数自适应律:

(55)

(56)

(57)

式中,cn>0为常数。

并根据上述参数自适应律和Young’s不等式以及假设4和假设5,式(54)可变换为

(58)

步骤 n+1定义

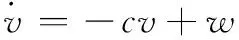
(59)

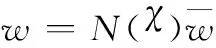
(60)

(61)

(62)

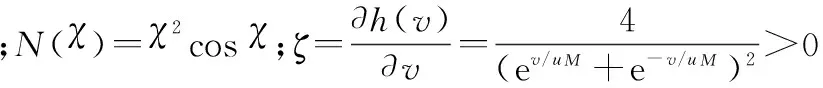
(63)

选择Lyapunov函数

(64)

则Vn+1关于时间t的导数为

(65)

为了保证闭环系统所有信号的有界性,选取Lyapunov函数Vsum

(66)

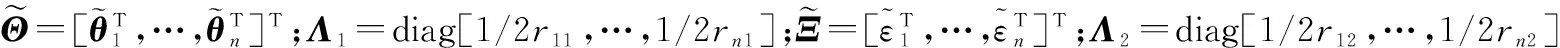
根据式(32),式(45),式(58)和式(66),函数Vsum关于时间t的导数为

(67)

式中

对式(68)积分,得

(68)

依据引理1和式(69)可以得到Vsum和χ有界的结论,且跟踪误差满足不等式:

(69)

(70)

从式(72)中不难得到闭环系统的跟踪误差终值有界。

根据以上Lyapunov稳定性理论的推倒证明,得到定理1。

定理 1对于控制方向未知的非线性系统式(1),依据反步法和模糊系统理论,设计出如式(59)所示的控制器和如式(24)～式(26)、式(42)～式(44)和式(55)～式(57)所示的自适应律。则形成的闭环系统所有信号半全局最终一致有界(semi-globallyuniformlyultimatelybounded,SGUUB)。

3　仿真分析

本文以一种吸气式高超声速飞行器在速度V=4 590.3m/s,高度h=33 528m的飞行条件下攻角的跟踪控制为对象,对控制系统进行仿真研究。

首先建立纵向特性方程[6,20]:

(71)

式中，α,q分别表示气动攻角和俯仰姿态角;m,V依次为高超声速飞行器的质量和沿机体轴向速度;L,T,Myy依次为施加在机体上的升力,推力和纵向俯仰力矩。式中所涉及的气动力与气动力矩计算表达式为

(72)

式(73)中气动参数的具体表达形式及参数的不确定度详见文献[21]。

由于舵面的偏转受到幅值限制,同时机体还会受到外界干扰的影响,故可将式(72)转换为

(73)

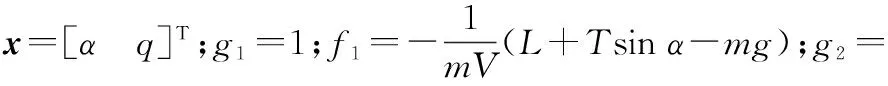
控制器参数分别为c1=13,c2=18,c3=7,c=6,γχ=0.008,τ1=0.015,τ2=0.045,χ(0)=0.4。

仿真中给定的攻角参考指令信号为yr=-22.5°cost+22°,设定飞行器舵偏角的偏转范围为±30°[6],取俯仰轴上受到的谐波干扰力矩大小为3×106sin(2t)。

图1中虚线表示为给定的攻角参考指令信号曲线,实线表示的为系统实际的跟踪响应曲线。从图中可以看出，在所设计的控制器的作用下,系统能够对给定的指令信号实现很好的跟踪,且跟踪误差一直保持在0的一个很小的邻域内。图2中舵偏角的输入信号用虚线表示,实线表示控制器舵偏角信号。图中显示不论舵输入信号发生多大的角度变化,舵偏角一直处于幅值范围内,并且能够实现对指令信号的跟踪。充分验证了本文设计方法在系统存在参数不确定和较大外界干扰时具有很强的鲁棒性能。

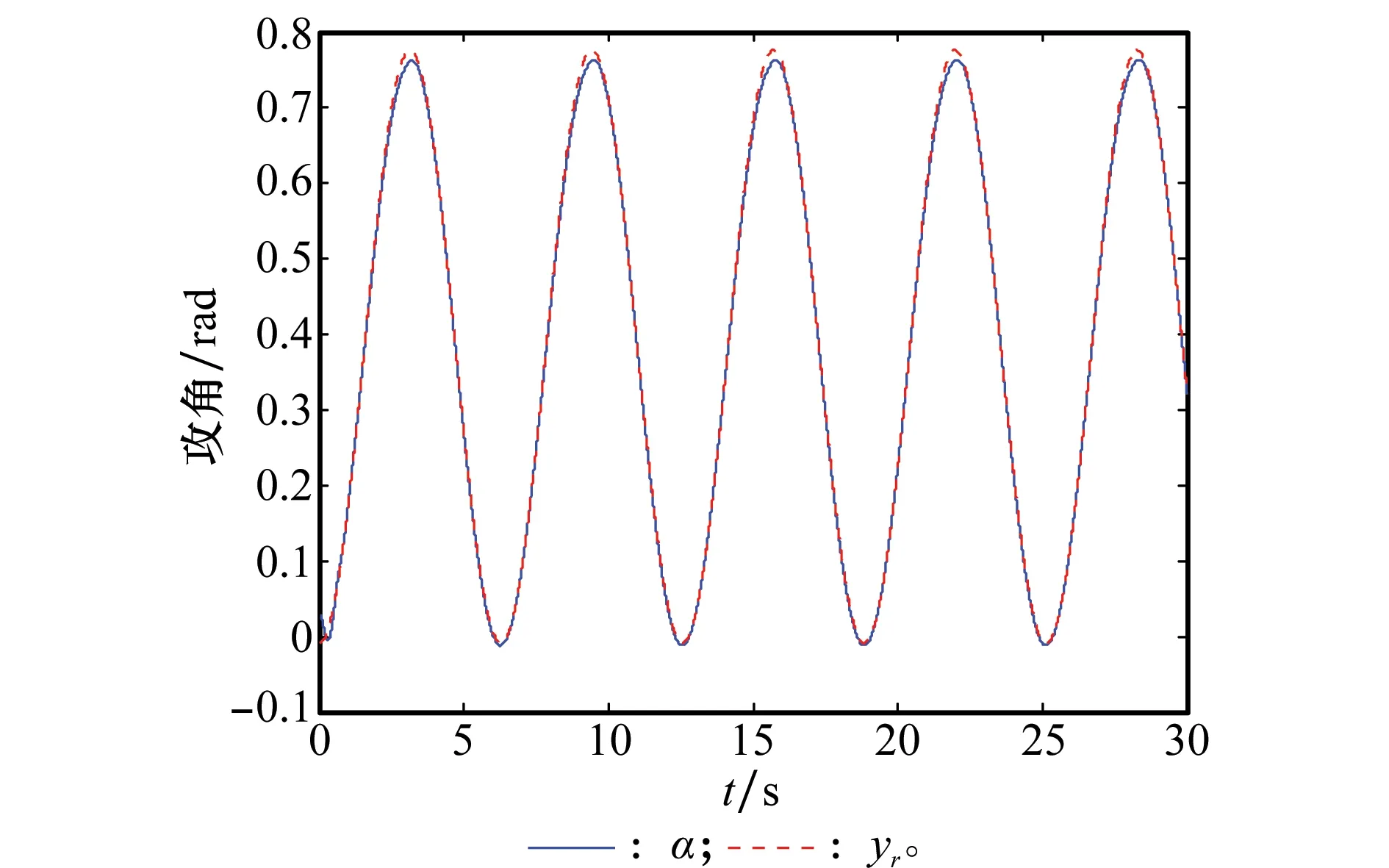
图1　输出响应曲线Fig.1　Curves of output response

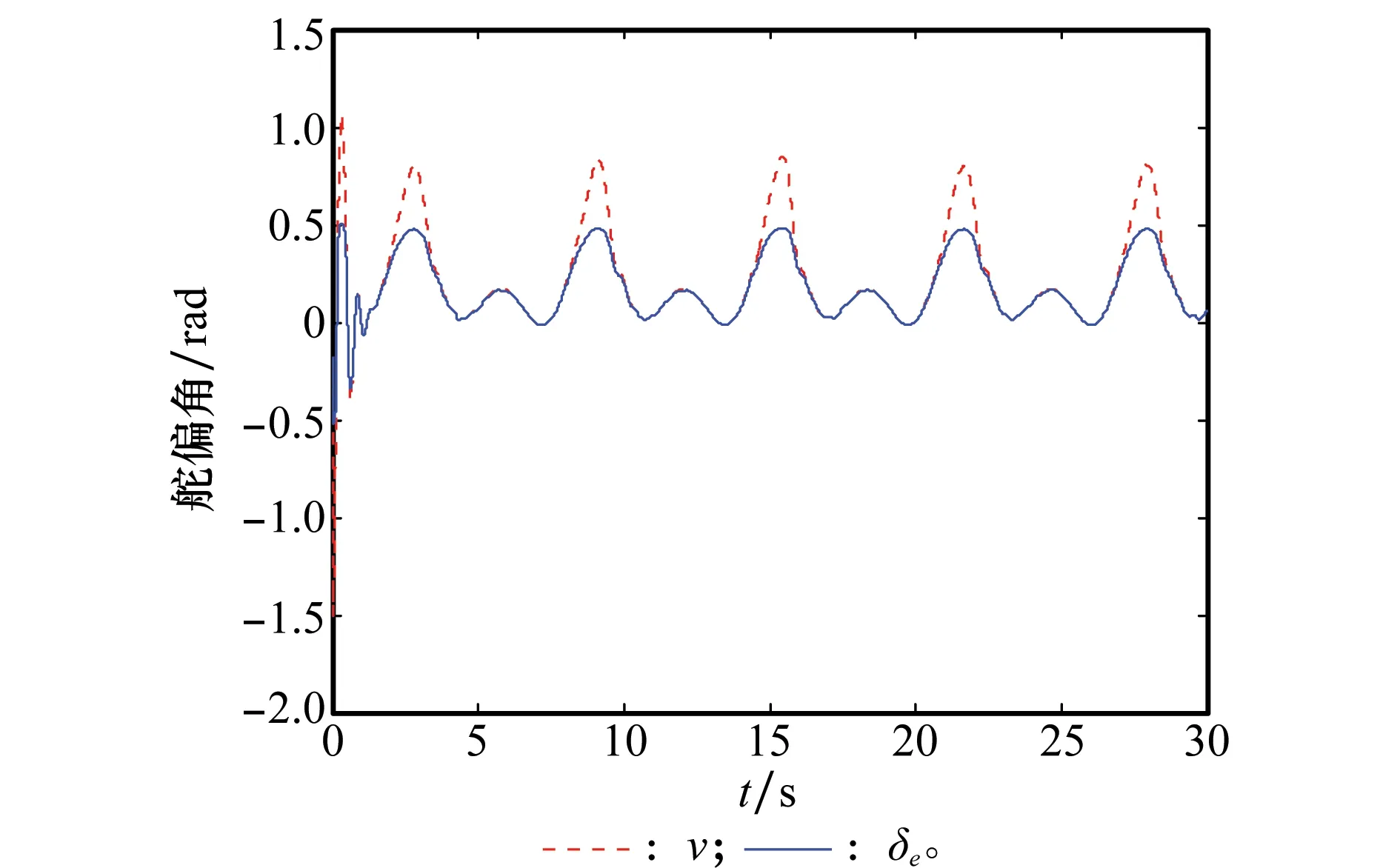
图2　系统控制信号Fig.2　Curves of control signals

4　结　论

文中针对一类不确定非线性系统设计了一种约束反步控制方法。首先通过变换系统形式和采用Butterworth低通滤波器解决了受控系统控制增益方向未知的问题,将反步法与DSC相结合,不但非常有效地解决了“微分爆炸”的难题,而且使得中间控制变量变得更加简洁,利于工程化的实现。引入双曲正切函数和Nussbaum增益函数有效地应对了普遍存在于非线性系统中的幅值约束问题。通过选取Lyapunov函数分析证明了系统中的所有信号是SGUUB。最后,依据本文提出的控制算法在高超声速飞行器的攻角跟踪控制回路上进行仿真验证,最终的结果验证了本文方法的有效性。

[1] Sonneveldt L, Chu Q P, Mulder J A. Nonlinear flight control design using constrained adaptive backstepping[J].JournalofGuidance,Control,andDynamics,2007, 30(2):322-336.

[2] Zhou H, Tan W. Anti-windup schemes for linear active disturbance rejection control[J].ControlTheory&Applications, 2014, 31(11): 1457-1463. (周宏, 谭文. 线性自抗扰控制的抗饱和补偿措施[J]. 控制理论与应用, 2014, 31(11): 1457-1463.)

[3] Jin Y Q, Liu X D, Qiu W, et al. Time-varying sliding mode control for a class of uncertain MIMO nonlinear system subject to control input constraint[J].ScienceChina(InformationSciences), 2010, 53(1): 89-100.

[4] Hu Q L, Zhang A H, Jiang C P, et al. Attitude control of satellite in process of orbit transfer with constraint input[J].JournalofHarbinInstitudeofTechnology, 2013, 45(5): 1-6.(胡庆雷, 张爱华, 姜成平, 等. 控制受限的卫星轨道转移过程中的姿态控制[J]. 哈尔滨工业大学学报, 2013, 45(5): 1-6.)

[5] Li Y M, Tong S C, Li T S. Direct adaptive fuzzy backstepping control of uncertain nonlinear systems in the presence of input saturation[J].NeuralComputation&Applications, 2013, 23(5): 1207-1216.

[6] Zhou Y L, Chen M. Robust control of nonlinear systems with input constraint based on disturbance observer[J].JournalofNanjingUniversityofScienceandTechnology, 2014, 38(1): 40-47.(周砚龙, 陈谋. 基于干扰观测器的输入受限非线性系统鲁棒控制[J]. 南京理工大学学报, 2014, 38(1): 40-47.)

[7] Liu J K, Wang M Z. Anti-windup control based on LMI and vibration suppression for the flexible spacecraft[J].ElectricMachinesandControl, 2014, 18(3):79-84.(刘金锟, 王明钊. 挠性航天器LMI抗饱和控制及模态振动抑制[J]. 电机与控制学报, 2014, 18(3):79-84.)

[8] Huang X L, Ge D M. Robust gain-scheduling control of hypersonic vehicle subject to input constraints[J].SystemsEngineeringandElectronics,2011,33(8):1829-1836.(黄显林,葛东明.输入受限高超声速飞行器鲁棒变增益控制[J].系统工程与电子技术,2011, 33(8): 1829-1836.)

[9] Kurtz M J, Henson M A. Input-output linerizing control of constrained nonlinear processes[J].JournalofProcessControl, 1997, 7(1): 3-17.

[10] Kong X B, Liu X J. Continuous-time nonlinear model predictive control with input/output linearization[J].ControlTheory&Applications, 2012, 29(2): 217-224.(孔小兵, 刘向杰. 基于输入输出线性化的连续系统非线性模型预测控制[J]. 控制理论与应用, 2012, 29(2):217-224.)

[11] Kanellakopoulos I, Kokotovic P V, Morse A S. Systematic design of adaptive controller for feedback linearizable systems[J].IEEETrans.onAutomaticControl,1991,36(11):1241-1253.

[12] Swaroop D, Hedrick J K, Yip P P, et al. Dynamic surface control for a class of nonlinear systems[J].IEEETrans.onAutomaticControl, 2000, 45(10): 1893-1899.

[13] Chen B, Tong S C, Liu X P. Fuzzy approximate disturbance decoupling of MIMO nonlinear systems by backstepping approach[J].FuzzySetsandSystems, 2007, 158(10): 1097-1125.

[14] Zhang T P, Wen H, Zhu Q. Adaptive fuzzy control of nonlinear systems in pure feedback form based on input-to-state stability[J].IEEETrans.onFuzzySystems, 2010, 18(1):80-93.

[15] Wen C Y, Zhou J, Liu Z T. Robust adaptive of uncertain nonlinear systems in the presence of input saturation and external disturbance[J].IEEETrans.onAutomaticControl, 2011, 56(7): 1672-1678.

[16] Wang L X. Stable adaptive fuzzy control of nonlinear systems[J].IEEETrans.onFuzzySystems, 1993, 1(2):146-155.

[17] Wang L X.Adaptivefuzzysystemsandcontrol——designandstabilityanalysis[M]. Beijing: National Defence Industry Press, 1995.(王立新. 自适应模糊系统与控制——设计与稳定性分析[M]. 北京:国防工业出版社, 1995.)

[18] Zou A M, Hou Z G. Adaptive control of a class of nonlinear pure-feedback systems using fuzzy backstepping approach[J].IEEETrans.onFuzzySystems, 2008, 16(4): 886-897.

[19] Kim E, Sungryul L. Output feedback tracking control of MIMO systems using a fuzzy disturbance observer and its application to the speed control of a PM synchronous motor[J].IEEETrans.onFuzzySystems, 2005, 13(6): 725-741.

[20] Tong S C, Li Y M. Observer-based adaptive fuzzy backstepping control of uncertain nonlinear pure-feedback systems[J].ScienceChina(InformationSciences), 2014, 57(1): 1-14.

[21] Xu H J, Mirmirani M D, Ioannou P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J].JournalofGuidance,Control,andDynamics, 2004, 27(5): 829-838.

Adaptivefuzzybacksteppingcontrolfornonlinearsystemwithunknowncontroldirectionandinputsaturation

WANGYong-chao,ZHANGSheng-xiu,CAOLi-jia,HUXiao-xiang

(Department of Automatic Control Engineering,Rocket Force Engineering University, Xi’an 710025, China)

AnadaptivefuzzybacksteppingcontrollerdesignmethodbasedonLipschitzconditionisdeve-lopedtodealwiththenonlinearsystemwithinputsaturationandunknowncontroldirection.Alongthecontrollerdesignprocess,thetransformedstyleandButterworthlowpassfilterareusedtosolvetheproblemoftheunknowncontroldirection.Byusingthefuzzylogicsystemtoidentifytheuncertainnonlinearfunctionsonline.ThehyperbolictangentfunctionandNussbaumareusedtohandletheinputsaturation.Thebacksteppingapproachiscombinedwiththedynamicsurfacecontroltechniquetosolvetheproblemof“explosionofcomplexity”.ItisshownwithLyapunovstabilitytheoremthattheproposedcontrolmethodcanguaranteethatallthesignalsoftheresultingclosed-loopsystemaresemi-globallyuniformlyultimatelybounded(SGUUB)inprobability.Finally,themethodisappliedforthecontroldesignoftheattackangleofthehypersonicvehicle.Simulationresultsshowtheeffectivenessofthepresentedmethod.

inputsaturation;nonlinearsystem;adaptivefuzzy;backsteppingapproach;hypersonicvehicle

2015-02-06；

2015-08-24；网络优先出版日期：2016-01-14。

国家自然科学基金(61304001,61304239)资助课题

TP273.2

ADOI:10.3969/j.issn.1001-506X.2016.09.26

王永超(1991-),男,博士研究生,主要研究方向为智能鲁棒控制。

E-mail:wyc031566@163.com

张胜修(1963-),男,教授,博士研究生导师,博士，主要研究方向为组合导航与飞行器制导控制。

E-mail:zsx1963@aliyun.com.cn

曹立佳(1982-),男,讲师,博士,主要研究方向为飞行器控制、仿真与决策。

E-mail:caolijia82@gmail.com

扈晓翔(1982-),男,讲师,博士,主要研究方向为非线性系统鲁棒控制。

E-mail:hxx820605@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160114.1658.008.html