恒温浴缸加水机制研究

王　强

恒温浴缸加水机制研究

王强

（重庆交通大学，重庆400074）

为了确定在没有辅助加热系统浴缸中加热水策略，文章通过对浴缸系统进行热力学分析，建立了浴缸关于时空双因素温度场模型；根据浴缸内部各空间点传热特点，将浴缸注入热水加热过程简化为点热源加热介质问题。利用能量守恒原理，根据傅立叶变换矢量法得出浴缸温度场的分布情况，求得注水点温度最高，边缘温度最低。然后基于浴缸温度场，在忽略人为影响因素条件下建立初级单目标优化模型，确定浴缸水体维持在39～40℃范围内注水流量最小值，结果表明当注水管流量为0.0028m2/s时可以达到预期目的。

能量守恒；傅立叶矢量变换；稳态热传导；优化

1　问题分析

为了研究恒温浴缸加热水机制，我们首先需要确定缸中水的热量（温度）分布，然后确定加水机制，以保证整个浴缸都接近初始温度而不浪费过多的水。所以我们把问题分为两部分：①建立依赖时间和空间的浴缸水温度场模型；②建立优化模型为洗澡人提供最佳热水控制策略。

2　基于时空依赖浴缸温度场模型建立

（1）问题分析。热水管注入水柱体积相对于浴缸体积来说较小，因此我们将加水维持水温的过程简化为点热源加热水浴过程。在不考虑热辐射因素和人因素的条件下，浴缸水是均匀的，可假设加热在半无限大均匀物体表面进行，利用傅立叶变换矢量法解出点热源的温度场。

（2）模型假设。①浴缸形状为椭圆形；②忽略热辐射造成的热量损失；③注水管直径远小于浴缸尺寸；④水龙头位置和溢水口位置一定。

（3）模型建立。在无限大导热体内，设点热源的发热量Q0为在任意时刻t，任意地点P（x，y，z）处的升温值χ，若热传导系数α为常量，溢出口散失热量为Qe，并且温度场初始状态是场内处处温度相等，热源发热后，温场内的温度分布必然对称与热源点。将坐标原点置于热源点上，令，因温度分布对称于原点，于是升温函数可记为θ（R，t）。按能量守恒法则可有：

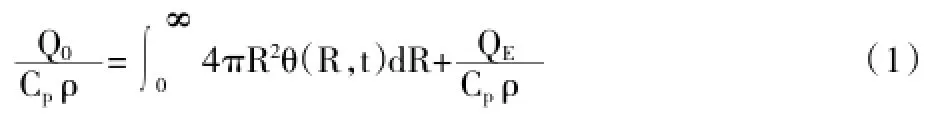
式中：Cp为温度场内物质的比热容，ρ为物质的密度。

在三维直角坐标系中，建立非稳态热传导微分方程，若Cp，ρ与无关，将非稳态热传导微分方程式作傅立叶变换，解出温度升高值：

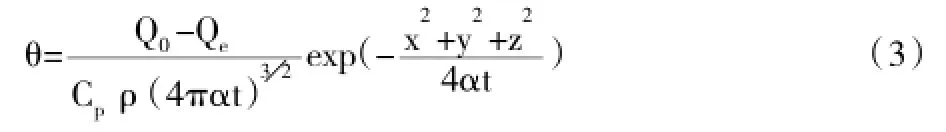
可得出在其他因素的确定的情况下，浴缸中水的温度分布情况如图1所示。

由于模型建立在四维纬度上，可通过限定一些因素降低模型纬度而得到温度场分布。如图1通过限定其他参数值，得到在z=0.35m平面上，温度分布情况。从图中可以看出在此平面上，浴缸水温分布在39～40℃之间，且注水口位置温度最高，边缘温度最低，是一个渐变过程，且温度关于注水点对称分布。

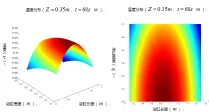
图1　温度分布图

图2　温度分布图

同理可得到在y=0.1m平面上，温度分布情况。如图2所示。和图1对比，虽然两种情况考虑的切面方向不一样，但温度分布规律是一致的。

3　单目标优化模型建立

（1）问题分析。根据研究，人体到的舒适温度范围是39～40℃之间，因此假设人在进入浴缸是浴缸水的初始温度在39～40℃之间，即问题在于保持浴缸水温度在39～40℃之间。利用模型二中浴缸水温度场模型，根据能量公式确定注水流量与注水热量之间的关系：Q0=f0ρCpT0，Qe=feρCpTe。其中Q0表示单位时间热水管注入浴缸所产生的能量，Qe表示单位时间溢水口流出水体算带走的热量，fe表示单位时间热溢水口排放水的流量，f0表示单位时间热水管注入水的流量，ρ热水管水流密度，Cp热水管水流比热容，T0热水管水流温度。

（2）模型假设。①为了保持水温，水龙头一直打开供热水；②流入水流量等于流出水流量；③环境温度保持不变；④注水管水温恒定且为70℃。

（3）模型建立。由模型一，可确定浴缸温度分布情况，据此建立以热水流量最小为目标函数的单目标优化模型如下：

minf0=S×V

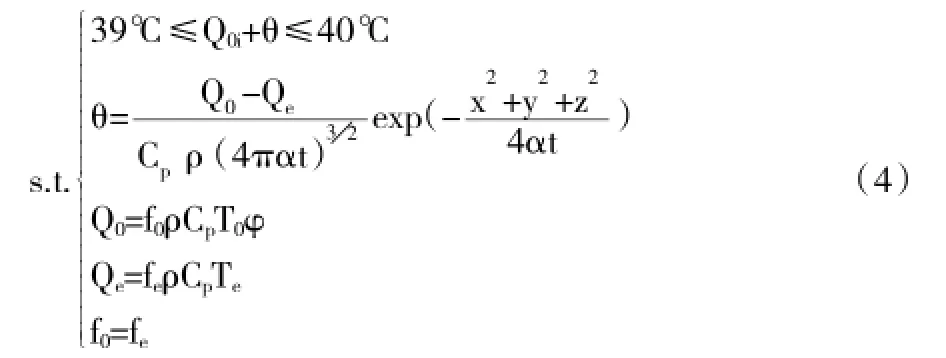
S为注水管直径，V为注水管水流速度，Q0i为任一点度的初始值，其值等于Q0，其他符号说明如前所述。

分析此模型可以看出，影响浴缸中水温度分布情况的因素同样是影响最小水流量的因素，利用MATLAB计算可得浴缸中无人时，在保证水温在39℃～40℃前提条件下，水管最小流量为0.00238。

［1］李金海，覃丽珍，蔡仁华.温泉水温变化的控制数学模型［J］.琼州学院学报，2006，（2）.

［2］李映文.温度知多少［J］.数理天地，2006，（7）.

Constant Temperature Bath Water Mechanism Research

WANG Qiang
（Chongqing Jiaotong University，Chongqing 400074，China）

In order todeterm inehotwateraddingstrategy in bathtubwithoutauxi1iaryheatingsystem，thispapercarriesoutther-modynamic ana1ysison thebathtubsystem，estab1ishesthebath crock ofthedua1factorsoftemperature fie1dmode1of timeand space， according toheattransfercharacteristicateachspacepointinside the tub，bath crock injectionofhotwaterheatingprocessissimp1i-fied to point heat source heating medium.Using the princip1e of conservationof energy，according to Fourier transform vector method to reach the bath temperature fie1d distribution of the highest water injection point temperature，temperature minimum edges.Then basedon thebath temperature，under the condition ofignoringhuman factorsaffecting theprimarysing1eobjectiveoptim izationmod-e1is estab1ished，determine the bath water to maintainwithin the scope of the 39℃to 40℃water injection f1ow minimum va1ue，the resu1tshowsthatwhen thewaterinjection pipe f1ow is0.0028m2/scanachieveexpected purpose.

energy conservation；Fourier vector transform；steady-state conduction；optimize

TP27

A

2095-980X（2016）03-0067-01

2016-02-23

王强（1994-），男，重庆奉节人，大学本科，主要研究方向：近海工程。