基于图论模型的成像卫星任务规划方法研究

黄瀚　张晓倩

(成都理工大学工程技术学院　自动化工程系，四川　乐山　614000)



基于图论模型的成像卫星任务规划方法研究

黄瀚*张晓倩

(成都理工大学工程技术学院自动化工程系，四川乐山614000)

成像卫星是目前在各领域应用极广泛的一类对地观测卫星，任务规划在其运控系统中也起着主导作用。针对成像卫星的任务规划研究主要建立了其成像任务及数传任务的图论模型。在此基础上研究了模拟退火算法对图论模型的求解效果。针对经典模拟退火算法的不足，加入了精英解保持策略和二次搜索过程。最后对比了改进的模拟退火算法与经典模拟退火算法应用于图论模型求解的效果。

成像卫星；任务规划；模拟退火算法

成像卫星是一类利用携带的成像载荷并对地表成像完成数据传输的对地观测卫星[1]。卫星的任务规划在整个卫星运行控制系统中处于中枢位置，对于成像卫星的功能实现起着决定性的作用。

成像卫星完成数据传输任务的途径主要有三条，分别是卫星与地面站完成数据传输、卫星与中继星完成数据传输和LEO星间数据传输。本文以成像卫星的成像任务及数据传输任务问题为研究对象，研究其任务规划的相关技术。

国内外对成像卫星任务规划相关问题的研究主要集中于任务规划预处理技术、任务规划建模和任务规划算法。

成像卫星任务规划预处理技术主要是根据用户的需求和卫星所携带资源的约束将原始任务分解为单次任务集合。对于任务分解技术集中与区域目标成像任务的分解技术。Walton J[2]、Rivett C[3]等将区域分解转化为集合覆盖问题。Lemaitre M[4]将区域目标按照成像模式分解为条带集合但是没有考虑到成像载荷的成像覆盖范围的重合性问题。

对于任务规划模型主要集中于图论模型、线性规划模型、约束模型等方面。Gabrel V[5]等将成像卫星任务规划描述为一个时间序有向无圈图模型，将任务规划转化为一个路径寻优问题。Vasquez M、Hao J K[6]等提出了以多维背包问题表示成像卫星任务规划，背包模型形式简单，可以表示简单的约束但是没法表达复杂的约束，难以应用于多星任务规划中。

针对不同的任务规划模型其求解算法也各不相同，主要有树搜索、动态规划法及各类优化算法。在各类算法中智能优化算法应用的较为广泛且规划效果也较好。

1　成像卫星任务规划问题描述及建模

1.1成像卫星任务规划的问题描述

在成像卫星的运行过程中，由于卫星的存储器的容量有限，在占用比例较高时需要执行数传任务释放空间。所以，以数传任务执行的起止时刻作为分段依据，把成像卫星的执行任务过程划分为数传段和成像段。

对于数据传输任务阶段，根据数传资源，其数传任务执行有两种情况。第一种情况是成像卫星与通信卫星间进行数据传输。第二种情况是成像卫星与地面站进行数据传输。需要注意的是成像卫星与地面站的数传方式可以是实传或回放。实传模式下成像卫星同时执行成像任务和数据传输任务。回放模式下，只能执行数据传输任务，将存储器重的数据传输给地面站。两者比较而言，实传模式时效性更好，所以在建模时可以理解为实传模式具有更高的优先级。

对于成像任务阶段，成像任务必须满足成像时间窗口、成像条件等约束才能成功执行。在建立起图论模型时就需要给其附加各类约束。

1.2成像卫星任务规划的图论模型

每个成像段对应生成一个成像段顶点，每个数传段根据数传方式不同对应生成三个顶点，这三个顶点在选择路径时只能选择一个顶点通过。依照上述方式建立各顶点并按卫星执行任务的时间顺序建立任务规划的有向图模型，如图1(a)所示。

图1　任务规划图论模型

图中符号含义如下所述：

“O”——表示为成像任务执行阶段；

“S”——表示为执行回放模式下的数传任务；

“R”——表示为执行实传模式下的数传任务；

“Q”——表示为仅执行成像任务；

“s”、“e”——分别表示起始和结束。

有向图中顶点“O”为成像任务阶段，根据成像任务的约束条件等信息，构成成像任务阶段的无向互斥图模型。将成像任务阶段中的单个成像任构成一个顶点。这一系列的顶点构成的集合就是用户所要求的成像任务集合。由于成像任务的各种约束条件使得某些成像任务出现冲突的情况，因此加入互斥关系构成如图1(b)所示的无向互斥图模型。

对于成像任务阶段的无向互斥图模型，其含义如下所述。

定义1顶点的互斥集合NO(v)。顶点v的互斥集合为

NO(v)={u|(u,v)∈E(O),u∈V(O),v∈V(O)}，v为互斥图中的任意顶点。

定义2顶点的度d(v)。顶点v的度为所有与顶点v具有互斥关系的其他顶点的个数，记为d(v)=|NO(v)|，v为互斥图中的任意顶点。

定义3顶点的权值w(v)。对于互斥图中的任意顶点v，顶点的权值是顶点所代表的成像任务的优先级。

定义4边的权值we(e)。边的权值表示连接的两个顶点的互斥关系。

无向图模型描述了成像任务目标之间的时间窗口约束关系，该模型简洁形象且易于理解。将无向图模型加入有向图模型中构成了成像卫星任务规划的图论模型。

1.3成像卫星任务规划的目标评价函数

根据成像卫星的任务特点及约束，确定任务规划的目标评价函数为

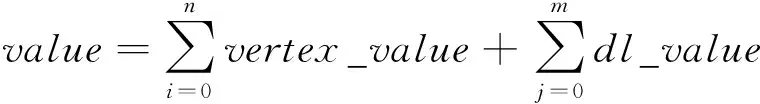
(1)

(2)

vertex_qz=∑(vertex_qz～×vertex_hc)

(3)

式中vertex_qz——为成像任务的优先级；

vertex_qz～——为与该成像任务冲突的成像任务的优先级；

vertex_hc——为两个成像任务之间互斥程度；

vertex_qz——为总互斥程度；

vertex_value——为成像任务的评价值；

dl_value——为数传任务的评价值；

value——为任务规划的总评价值。

2　改进的模拟退火算法及其仿真

2.1模拟退火算法及其改进算法简述

物质经由熔化状态逐渐冷却达到结晶状态的物理过程中，物质的内能随之衰减直至最低[7]。而优化问题求解的过程与物质的退火过程相似，所以在最优问题的求解过程中加入内能函数，利用Metropolis准则，确保在温度趋于收敛时，有更大的概率接受最优解。模拟退火算法已经由数学方式证明其有一定概率搜索到最优解。

对于经典模拟退火算法，若温度更新函数的参数选择偏小会导致降温过程过快，最终搜索不到全局最优解；若该参数选择偏大，则需花费大量时间去搜索全局最优解，使得算法的收敛性变差。所以对其作了适当的改进，改进的模拟算法如图2所示。

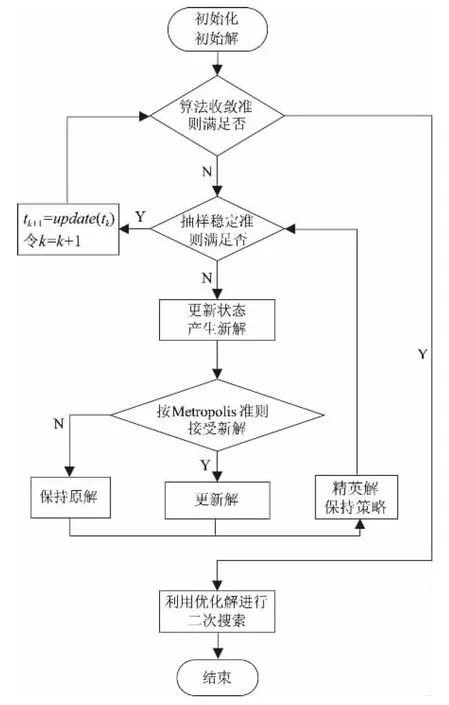
图2　改进的模拟退火算法程序流程图

改进的模拟退火算法相比于经典的模拟退火算法，增加了精英解保持策略和二次搜索过程。在模拟退火算法的退火过程中保持精英解可以避免因温度更新参数选择过大导致收敛性变差的后果。在结束模拟退火算法后再次执行二次搜索可以避免因温度更新参数选择过小导致降温过程过快的后果。

2.2基于MATLAB的仿真与结果分析

在应用模拟退火算法的时候，目标评价函数值f即为内能函数E，温度T则是控制整个算法收敛的参数t，由初始可行解S0和控制参数初值t开始，进行“产生新解-计算新状态-更新状态”的迭代过程，直到其满足算法收敛条件。在模拟退火过程中，由算法收敛准则决定是否得到最终解，由抽样稳定准则决定是否更新控制参数，由Metropolis准则决定更新的状态。

仿真中初始温度为t0=100 ℃，温度更新函数为tk+1=0.93tk。

算法收敛准则采用设置温度控制参数的阈值，当温度控制参数到达该阈值，停止搜索。这种收敛准则普遍适合于各种应用背景，温度控制参数阈值为t=1e-5。

抽样稳定准则采用设置内循环迭代次数的方式，当满足条件时，更新控制参数。

仿真中对于新状态的更新方式与任务类型息息相关。针对成像任务有以下两种更新方式：

(1)互换操作是指随机将成像任务序列中的一个顶点换成该顶点的互斥集合中某一个顶点；

(2)插入操作是在成像任务序列中插入与任务序列中现有顶点都不互斥(即边的权值为0)的某个顶点。

对于数据传输任务，则通过改变数传任务的通信模式来更新其状态。

由于成像卫星任务规划为组合优化问题，状态编码可以是0-1编码方式和整数编码方式。分析了在算法处理中两种编码方式带来的差异，发现0-1二进制编码方式处理起来更为简单。将状态编码为0-1二进制码，采用取反操作代替插入操作和替换操作进行状态的更新。

在仿真中假定任务规划的图论模型有两个成像段和两个数传段，两个成像任务段分别有16和9个成像任务。采用经典模拟退火算法解算该模型，其程序运行时间为2.194 250 s，其目标评价值变化如图3所示。

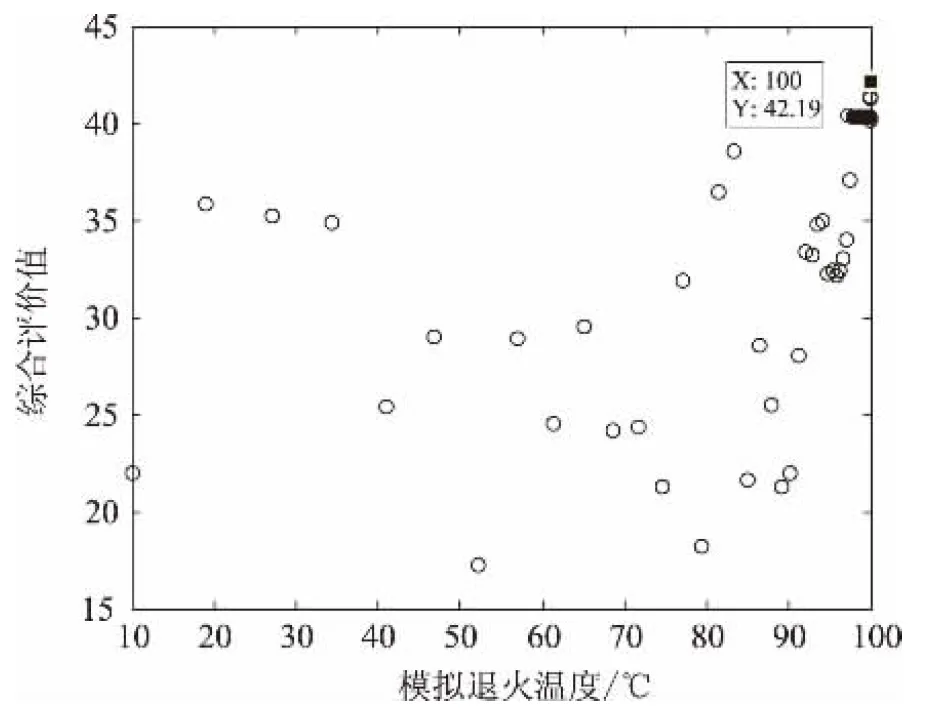
图3　基于经典模拟退火算法的评价值变化图

由图3可以看出模拟退火算法在运行过程中有一定的概率接受较差的解，这扩大了搜索可行解的范围。最终规划结果为：

成像段A的方案为[1,0,1,1,1,1,1,0,1,1,0,0,0,1,1,1]；

成像段B的方案为[0,1,1,1,1,0,0,0,1]；

两个数传顶点的工作模式均为回放模式；

最终的目标评价值为42.19。

规划结果中“1”表示该成像任务被选定在任务规划的最终方案中，“0”则表示不选择该任务。从图3中解的更新可知，应用经典模拟退火算法时，不会只限于更好的解的周围去搜索，而是以一定的概率接受次优解。但是由于经典模拟退火算法的自身缺陷，丢失了搜索过程中得到的一个最优解。

采用改进的模拟退火算法解算该图论模型，其程序运行时间为2.015 32 s，其目标评价值如图4所示。

图4　基于改进的模拟退火算法的评价值变化图

其规划结果：成像段A为[1,0,1,1,1,1,1,0,1,1,0,0,0,1,1,1]，成像段B为[0,1,1,1,0,1,0,0,1]，两个数传顶点的工作模式均为回放模式，任务方案的目标评价值为42.67。

对比经典模拟退火算法和改进的模拟退火算法的规划结果后，可以看出当增加了精英解保持环节后，能够保证不丢失搜索过程中的最优解。改进了任务序列编码方式之后，也使得程序的执行时间大大减少，能够很快的搜索到全局最优解。而经典模拟退火算法由于Metropolis准则接受新解的随机性，难以快速收敛到最优解。

3　结束语

成像卫星的任务规划在其运行中有着举足轻重的作用，研究其任务规划技术对成像卫星的发展有着重要意义。通过成像卫星的任务规划图论模型可以简洁明了的验证各类优化算法的应用效果。仿真结果表明对模拟退火算法适当改进之后可以明显改善其算法的收敛性和寻最优解的能力。改进的模拟退火算法在成像卫星任务规划中取得不错的效果，对于实际的成像卫星任务规划也具有指导意义。

[1]葛榜军, 廖春发. 总装备部卫星有效载荷及应用技术专业组应用技术分组[M]. 卫星应用现状与发展，北京: 中国科学技术出版社, 2001: 124-130.

[2]Walton J T. Models for the management of satellite-based sensors[D]. Massachusetts Institute of Technology, 1993.

[3]Rivett C, Pontecorvo C. Improving satellite surveillance through optimal assignment of assets[R]. Defence Science and Technology Organisation Edinburgh (Australia) Intelligence Surveillance Reconn Div, 2003.

[4]Lemaitre M, Verfaillie G. Earth Observation Satellite Management[J]. Constraints, 1999,4(3):293-299.

[5]Gabrel V, Vanderpooten D. Enumeration and interactive selection of efficient paths in a multiple criteria graph for scheduling an earth observing satellite[J]. European Journal of Operational Research, 2002, 139(3): 533-542.

[6]Vasquez M, Hao J K. A “logic-constrained” knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observation satellite[J]. Computational Optimization and Applications, 2001, 20(2): 137-157.

[7]江加和, 宋子善. 模拟退火算法在连续变量全局优化问题中应用[J]. 北京航空航天大学学报, 2001, 27(5): 556-559.

(责任编辑陈葵晞)

黄瀚，男，江西吉安人。助教，硕士。研究方向：控制理论与控制工程。

TP273

A

2095-4859(2016)02-0155-04