线阵CCD光谱采集系统的自适应滤波降噪

潘　宇,罗永道（云南师范大学物理与电子信息学院,云南昆明 650500）

线阵CCD光谱采集系统的自适应滤波降噪

潘宇,罗永道
（云南师范大学物理与电子信息学院,云南昆明 650500）

为了便于对微型线阵CCD光谱采集系统采集的光谱数据进行分析,需要对光谱数据采集过程中出现的噪声进行降噪处理,以提高光谱数据的信噪比。首先,根据线阵CCD参数指标,设计了一种硬件降温结构,并用它对线阵CCD进行降温去噪。接着,根据递归最小二乘自适应滤波算法对采集好的水样品光谱数据进行去噪处理,然后和未去噪的水样品数据对比。实验表明,硬件电路降温去噪能够衰减线阵CCD上的暗电流噪声,使用递归最小二乘自适应滤波方法能够有效消减光谱采集系统中光谱数据的噪声。

光谱学；线阵CCD；自适应滤波；去噪

引 言

近年来,光谱分析技术逐渐被广泛应用于环境、食品安全监测、物质分析等领域,在天文学和卫星监测领域也有广泛使用。正是由于各个领域对这门技术的推广和普及使得光谱技术逐渐走向成熟。与传统的电化学分析和色谱分析方法相比,光谱分析技术更具有操作简便、重复性好、测量精度高和检测快速的优点［1］。光谱仪的小型化、微型化,使得光谱仪的色散距离变短,仪器内部空间密度变得更加紧凑,这使得整个仪器的分辨率、灵敏度、信噪比等性能将更多地依赖于光电探测器件CCD上［2］。然而在使用光谱仪器采集被测物体光谱数据的过程中,由于受到仪器线阵CCD品质因素的影响或者机器发热量高导致仪器内部的CCD、电阻等元件的电流热噪声变大使得被测物质的光谱数据含有噪声,最终在对被测物质进行成分分析时误差增大［3］。因此对原始的光谱数据进行去噪处理是鉴定物质准确性的必要保证。

光谱数据去噪处理的好坏与否,会影响物质成分分析的结果和仪器的预测精度［4］。目前,常用的光谱去噪方法主要有硬件去噪和软件去噪两种。在软件去噪方面,常用的有微分法、平滑法、傅里叶变换和小波变换等［5］。用微分法对光谱数据去噪能够消除基线漂移、强化谱带特征,但去噪效果不好。平滑法可以衰弱信号中的高频噪声,但有用的光谱信号也会被衰减,造成光谱信号失真。傅里叶变换法对平稳信号有很好的去噪效果。小波变换法可以只对特定频率或某一时刻的局部信号进行频谱处理,而不影响整体信号,去噪效果好,但小波变换运算量大,实现去噪效果的速度较慢［6］。自适应滤波方法不仅具有运算量小、速度快、可递推实时处理的优点,而且它不需要已知信号的统计特性,它是通过一种自适应算法来调节自身滤波参数从而达到最好的滤波效果［7］。正是由于自适应滤波的这些优点,使其广泛应用于通讯、激光、医学等领域。

1　线阵CCD光谱采集系统中噪声的来源和硬件电路的降噪设计

实验中所采用的小型线阵CCD光谱采集系统是自主研发的,它能够采集220～800 nm波长范围的紫外可见光谱数据。该系统采用了交叉非对称式的Czerny-Turner光学结构如图1所示。仪器中采用的线阵CCD为东芝TCD1304AP,属于中低端水平的CCD。在该线阵CCD光谱数据采集系统中,噪声的来源有很多种。其中主要的噪声来源是线阵CCD,它的输出噪声主要有暗电流散粒噪声、光子散粒噪声、输出放大器噪声等。此外在信号的传输过程中还会夹杂着一些电子器件噪声。这些噪声都是一些具有均匀频谱的低频噪声和高斯白噪声［8-9］。

为了去除CCD上的散粒噪声,实验中采用硬件温控去噪方法和软件自适应滤波方法。在硬件温控去噪方法中,采用了TEC半导体制冷技术,用EP3-06E058-RTO型号的TEC制冷芯片对CCD进行控温去噪,制冷装置如图2所示。图3为半导体制冷片控温驱动板实物图,通过它来控制半导体制冷。图2中散热铝块和风扇的作用是迅速散去TEC制冷片上产生的热量,使TEC制冷片能够正常工作。

图1　Czerny-Turner结构Fig.1　Czerny-Turner structure

图2　硬件温控示意图Fig.2　The temperature control diagram

图3 硬件温控实物图Fig.3　The temperature control graph

图4中显示的光谱曲线是没有进行降噪处理的原始水样品光谱曲线,为了便于看清噪声,所以图中显示的曲线是从水样品光谱曲线中选取了一段噪声明显的曲线经过放大之后的图像。从图4中可以看出在没有对线阵CCD进行降温时采集到的水样品光谱数据中存在着像锯齿型一样的噪声。实验中的光谱数据来自于自主研发的小型线阵CCD光谱采集系统,由于在设计PC机软件时没有直接对该系统获取的光谱数据进行波长标定,所以图4中的横坐标是光谱仪上线阵CCD的像素点而不是波长,纵坐标是线阵CCD输出的光的强度信号。图5表示的是使用控温去噪处理后的水样品光谱曲线图,从图中可以看出水样品光谱曲线上仍然还存在锯齿型噪声［10］,只是相对于原始光谱曲线的噪声幅度稍微减弱了。这说明硬件降温去噪的方法在实际应用中不能完全滤除由线阵CCD产生的散粒噪声,只能减弱CCD的暗电流噪声。

图4　原始水样品光谱图Fig.4　The original water sample spectrum graph

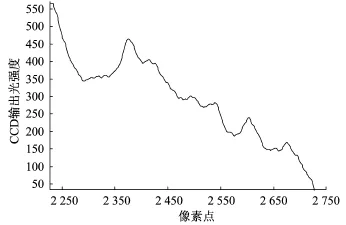
图5　控温去噪后的光谱图Fig.5　The denosing spectrum graph

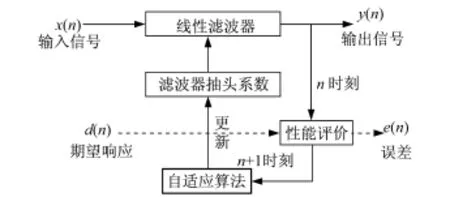
图6　自适应滤波器结构图Fig.6　Self-adaptive filter structure

2　最小二乘自适应滤波器的算法构建

自适应滤波就是利用性能评价函数（代价函数）对前一时刻得到的滤波器输出结果与期望得到的结果进行性能评价,并根据评价的结果来自动调节现在时刻的滤波器的抽头系数,以适应信号和噪声未知的或随时间变化的统计特性,从而实现最优滤波。实现自适应滤波器的方法有很多种,比如递推最小二乘法、卡尔曼滤波法、最小均方误差法等,其中递推最小二乘法的抑制处理效果及工程实现得到了很好的应用。实验中采用了递推最小二乘法,其结构如图6所示。图中输入信号是由线阵CCD光谱采集系统采集到的水样品光谱数据提供,这些原始光谱数据在已知n=0时刻滤波器抽头系数的情况下即刚开始时横向滤波器的抽头系数,通过简单更新,求出n=1时刻下滤波器的抽头系数。再由n=1时刻滤波器的抽头系数更新n=2时刻的滤波器抽头系数,直到n时刻,其中n为横向滤波器的阶数。而整个更新滤波器抽头系数的过程就是递推最小二乘算法。

自适应最小二乘算法在第k个采样点对应的一组输入信号xk（i）,i=0,1,…,n,那么算法对应的输出为

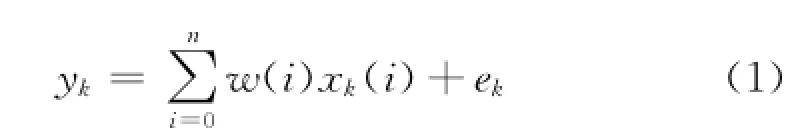
式中:n为滤波器阶数；ek为误差项；w（i）为滤波器的第i项抽头系数。要实现用上一时刻的滤波器抽头系数更新下一时刻滤波器的抽头系数,需要满足让性能评价函数的值达到最小,实验中采用了指数加权的误差平方和,即

式中λ为遗忘因子,λ的作用是离n时刻近的误差给予较大的权重,离n时刻远的误差给予较小的权重,确保在过去某一时间段内观察到的数据被“遗忘”,从而使滤波器可以工作在平稳状态下。其中ε（i）误差因子的表达式为

式中:d（i）为期望响应；wH（n）x（i）是滤波器的输出响应y（i）。把式（3）代入式（2）中得加权误差平方和的完整表达式

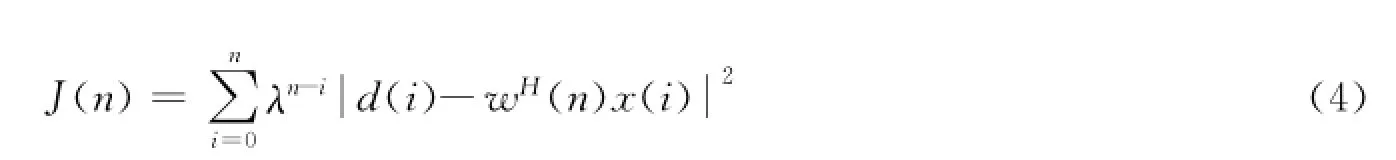
从式（5）、式（6）看出指数加权最小二乘法的解被转化为了维纳滤波器的形式。

对式（5）进行化简,并根据矩阵求逆引理得

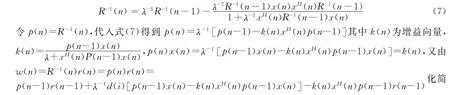
得更新权向量w（n）=w（n—1）+k（n）ε（n）,其中w（n）为滤波器该时刻的抽头系数,w（n—1）为滤波器上一时刻的抽头系数。由此整个递归最小二乘自适应算法就推导完成了。总结上面的推导过程,归纳出实验中最小二乘自适应算法的实现方法流程如下:

（1）选取合适的遗忘因子λ,0＜λ＜1；

（2）算出FIR滤波器的初始抽头系数w0,w1,…,wL—1；

（3）对于每一时刻的n=1,2,3,…,N（N是FIR滤波器的阶数）,分别计算:p（n）,ε（n）,w（n）；

（4）把算好的w（n）的数据更新到n+1时刻下FIR滤波器抽头系数中。

3　测量实验与结果

3.1FIR滤波器结构选取

实验中用递推最小二乘自适应滤波方法对水样品数据进行去噪时,通常需要选取合适的横向滤波器作为整个滤波算法的基础。通用的滤波器设计方法有窗函数法和频率取样法。窗函数法是从时域进行设计的,而频率取样法是从频域进行设计的。从设计复杂度比较,窗函数法要比频域取样法简单。从滤波效果比较,窗函数法设计的滤波器在通带和阻带的性能优于频率抽样法［7］,所以试验中采用了窗函数法设计FIR滤波器。常见的窗函数有矩形窗、Hann（汉纳）窗、Hamming窗、Blackman（布莱克曼）窗、Kaiser（凯泽）窗,其中矩形窗、Hann（汉纳）窗、Hamming窗、Blackman（布莱克曼）窗的窗函数是固定的,因而一旦选则了某一种窗函数,设计出的FIR滤波器在阻带的衰减就是确定的。Kaiser窗是一种应用广泛的可调窗,可以根据滤波器的衰减指标来确定窗函数的形状［11-12］。由于实验中线阵CCD光谱采集系统中的噪声的频带是存在于整个频率范围内的,而且所测量光谱信号的频率范围也是不确定的,这就让我们无法预知要滤除的噪声的频带范围,由于Kaiser（凯泽）窗具有可调性,所以实验中通过PC机端编写的软件,选择Kaiser窗作为FIR横向滤波器的主要框架。表1中第一行数据表示的是使用Kaiser（凯泽）窗,在通带截屏为0.001和阻带截屏为0.1时的滤波器抽头系数,从表中可以看出该滤波器的阶数是20阶。

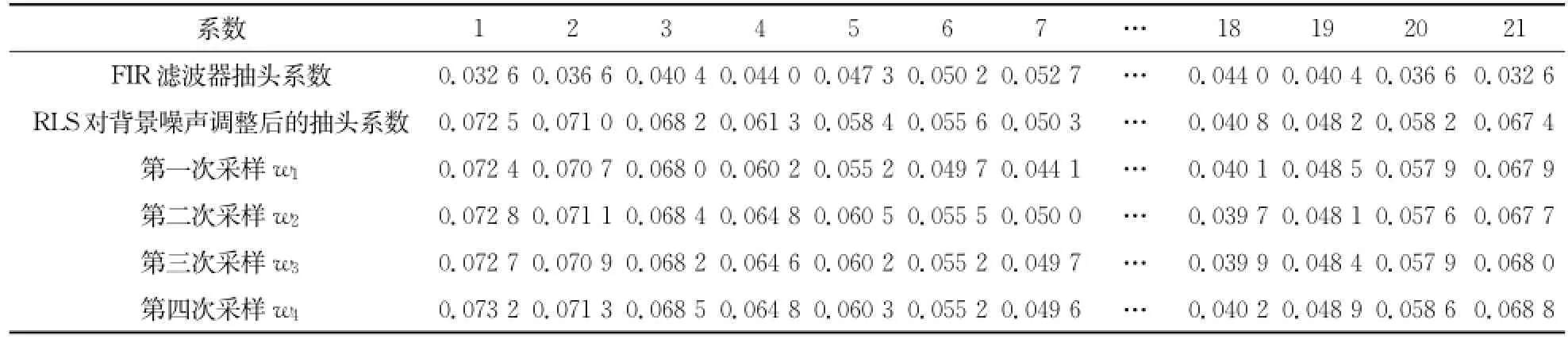
表1　RLS自适应算法对FIR滤波器抽头系数的调整Tab.1　Using RLSself-adaptive algorithm to adjust FIR filter tap coefficient

3.2递推最小二乘自适应滤波器对水样品去噪处理结果

从上面的FIR滤波器中得到的抽头系数共有20阶,选取最小二乘自适应滤波器的遗忘因子λ为0.99。在递推最小二乘算法中需要给出一个理想的光谱数据作为期望值然后减去FIR滤波器输出的数据从而得到误差因子,进而计算并更新下一时刻滤波器抽头系数。所以期望值的选取是算法中重要的环节。由于各种物质的光谱数据事先是不知道的,期望值的选取就变得很困难,为了避免选取的期望值引入其它噪声和误差,实验中首先在暗室里测得了线阵CCD光谱采集系统的背景噪声,由于在理想环境下线阵CCD在无光照条件下输出值是0,所以实验中用d（i）=a作为期望值。其中i=0,1,…,n；a为常量, n为滤波器的阶数。然后对背景噪声进行递推最小二乘滤波得到一组滤波抽头系数,再用该组抽头系数对水样品数据进行去噪。最后用去噪后的水样品数据作为水样品的期望值,对同样的水样品进行自适应去噪。图7为背景噪声和用最小二乘滤波法滤波后的曲线图。

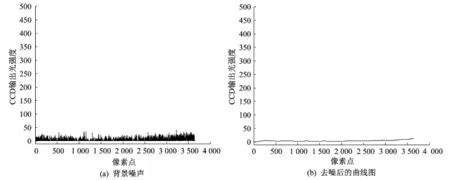
图7　线阵CCD光谱采集系统的背景噪声和自适应去噪后的曲线图Fig.7　Linear CCD spectral acquisition system of background noise and after denoising graph

表1中第二行数据表示对线阵CCD光谱采集系统进行自适应滤波后抽头系数的改变情况。图8所示的是用对背景噪声自适应去噪后的滤波器抽头系数对原始水样品数据进行FIR滤波后的曲线图,并用该曲线的光谱数据作为期望值。实验中保持水样品不变,连续采集9组光谱数据。由于每次采集,线阵CCD光谱采集系统上产生的噪声都不一样,所以得到的效果如图9所示。分别对这9组原始光谱数据进行自适应滤波,得到的效果如图10所示。

从图9、图10中可以看出对于线阵CCD光谱采集系统每次产生的不同的随机散粒噪声,该算法都能够对其进行自适应滤波。由于光源氙灯发光的不稳定,影响了线阵CCD的光强输出。所以图中看到的曲线的光强幅度会有些波动。从表1中的数据也可以看出随着取样次数的不同,每次的滤波器抽头系数也不同,而且最小二乘自适应滤波器让原始光谱数据在可容许的最小误差范围内使其逐渐向期望的光谱数据收敛。

图8　期望的水样品光谱数据Fig.8　The desired water sample spectral data

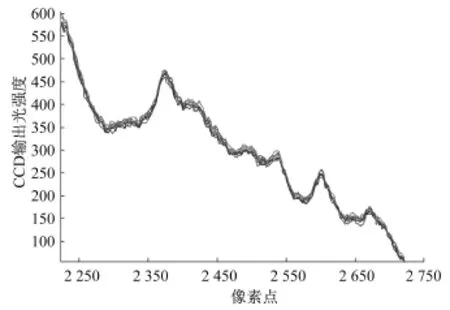
图9 9组水样品光谱图Fig.9　Spectra of 9 groups of water sample

图4、图5、图10相比较,得出最小二乘自适应滤波器的滤波效果很好,能够去掉线阵CCD所产生的散粒噪声。

4　结 论

通过对线阵CCD光谱采集系统采集的初始水样品的光谱数据进行硬件温控去噪和最小二乘自适应滤波去噪。从二者所处理的光谱曲线图来看自适应滤波算法的去噪效果比硬件去噪效果好,通过计算两种去噪结果的RMS值,硬件温控的S/N为2581：1,而自适应滤波算法的S/N为3081：1,因此自适应滤波去噪可以有效的提高光谱数据的可靠性,在实际仪器制造中能够节约设计成本。不足的是使用最小二乘自适应滤波算法对原始水样品进行去噪所消耗的时间为0.598 s,对于速度要求较高的场合不适于在PC机端选择最小二乘自适应滤波方法进行去噪。

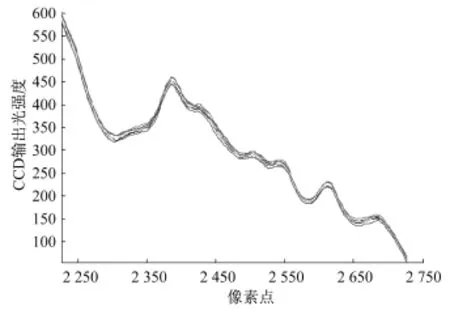
图10　9组水样品自适应去噪后的光谱图Fig.10　The spectrogram after adaptive filter

［1］ 黄福荣,罗云瀚,郑仕富,等.全血胆固醇、甘油三酯近红外光谱分析与模型优化［J］.光学学报,2011,31（10）:1030001.

［2］ 李正刚.微小型光谱仪低噪声、大动态范围方法研究［D］.长春:中国科学院研究生院（长春光学精密机械与物理研究所）,2010.

［3］ 李慧,蔺启忠,王钦军,等.基于小波包变换和数学形态学结合的光谱去噪方法研究［J］.光谱学与光谱分析,2010,30（3）:644-648.

［4］ 蔡剑华,王先春.基于经验模态分解的近红外光谱预处理方法［J］.光学学报,2010,30（1）:267-271.

［5］ 严衍禄.近红外光谱分析基础与应用［M］.北京:中国工业出版社,2005:103-107.

［6］ 李素文,谢品华,李玉金,等.基于小波变换的差分吸收光谱数据处理方法［J］.光学学报,2006,26（11）:1601-1604.

［7］ 陈从,卢启鹏,彭忠琦.基于NLMS自适应滤波的近红外光谱去噪处理方法研究［J］.光学学报,2012,32（5）:0530001-1-6.

［8］ 佟首封,阮锦,郝志航.CCD图像传感器降噪技术的研究［J］.光学精密工程,2000,8（2）:140-145.

［9］ 田岩涛,常丹华,张彦.线阵CCD信号的小波去噪方法研究［J］.传感技术学报,2005,18（2）:250-253.

［10］ 周丹,王钦军,田庆久,等.小波分析及其在高光谱噪声去除中的应用［J］.光谱学与光谱分析,2009,29（7）:1941-1945.

［11］ 姚海燕.FIR数字滤波器设计窗函数法与频率抽样法比较［J］.安阳工学院学报,2007（6）:51-53.

［12］ 陈后金,薛健,胡健.数字信号处理［M］.2版.北京:高等教育出版社,2008:158-197.

（编辑:张 磊）

Adaptive filtering denoising for linear CCD spectral acquisition system

PAN Yu,LUO Yongdao
（Department of Physical and Electronic Information,Yunnan Normal University,Kunming 650500,China）

In order to analyze the spectral data collected by a linear CCD spectral acquisition system,it needs to solve the spectral noise that appeared in the process of data collection,to improve the signal-to-noise ratio of the spectral data.First,According to the linear CCD parameter,we design a kind of cooling hardware structure and use it to cool the denoising linear CCD.At the same time,based on recursive least square adaptive filter algorithm,water sample spectral data is dealt with to compare with the noise of water sample data.Experimental results indicate that hardware circuit denoising is not able to completely remove the thermal current on the linear CCD noise.Using the recursive least square adaptive filter method can effectively reduce noise in the spectrum acquisition system.

spectroscopy；linear CCD；adaptive filter；denoising

O 433.4

A

10.3969/j.issn.1005-5630.2016.02.014

1005-5630（2016）02-0167-06

2015-07-29

国家自然科学基金（61168003）

潘 宇（1990—）,男,硕士研究生,主要从事成像光学方面研究。E-mail:350148275@qq.com

罗永道（1969—）,男,副教授,主要从事光谱仪器技术方面的研究。E-mail:dhlyd300@163.com