流感病毒组成蛋白质序列的分析与预测

靳佩轩，高 洁

（江南大学 理学院，江苏 无锡214122）

流感病毒组成蛋白质序列的分析与预测

靳佩轩，高 洁*

（江南大学 理学院，江苏 无锡214122）

在NCBI数据库中获得1902—2013年关于流感病毒10种组成蛋白的所有氨基酸序列，在MATLAB中采用大数据编程分析，结合详细的HP模型，并基于CGR-WALK模型的方法将全部流感病毒蛋白质序列转化为数据形式，引入时间序列ARFIMA（p，d，q）模型来拟合所有序列，分析10种组成蛋白的序列在近80年的变化趋势，并对其未来10年的发展趋势进行预测.通过分析可以发现，其对流感病毒变异趋势的预测有很好的效果，这为基于大数据分析流感病毒蛋白质序列，预测流感病毒的爆发提供一定的的研究参考价值.

流感病毒；蛋白质序列；详细HP模型；CGR-WALK模型；ARFIMA（p，d，q）模型

流感病毒为负向单链RNA病毒［1］，自身具有很强的变异性，历史上多次流感大流行都是由其新的亚型和以往出现过的亚型经过变异再次出现，人类由于缺乏对其的免疫力而导致流感病毒在人群中快速传播。

目前对流感病毒蛋白质序列的研究上，刘娟等用时间序列模型识别，预测流感病毒的DNA序列。张玲用时间序列模型识别，预测甲型H1N1流感病毒蛋白质序列在未来年份的变异情况取得很好的预测效果［2-5］。作者以时间序列分析研究为基础，分别选取数据库中现有的从1902—2013年间近100年的流感病毒的10种组成蛋白：Hemagglutinin，MatrixProtein 1，Matrix Protein2，Neuraminidase，Nonstructural Protein1，Nonstructural Protein2，Nucleocapsid Protein，Polymerase PA，Polymerase PB1，Polymerase PB2等作为研究对象。运用大数据处理方法将全部序列以HP模型为基础进行数据化转换，并利用CGR-WALK建模，再采用时间序列ARFIMA（p，d，q）模型分析流感病毒每种蛋白质的变异规律和未来的发展趋势，以蛋白质序列整体为研究对象，从宏观研究分析的角度为研究流感病毒在之后几年内的变异情况提供预测依据，并能够为相关流感病毒的预测研究提供重要的研究思路和方法。

1　材料与方法

1.1材料

选取NCBI数据库中1902—2013年之间所有流感病毒的10种组成蛋白质序列，即Hemagglutinin，Matrix Protein 1，Matrix Protein 2，Neuraminidase，Nonstructural Protein 1，Nonstructural Protein2，NucleocapsidProtein，PolymerasePA，Polymerase PB1，Polymerase PB2蛋白质序列作为作者的研究对象进行分析。（NCBI：http：//www.ncbi. nlm.nih.gov/.）

1.2方法

1.2.1蛋白质序列基于详细的HP模型数据化构建CGR-WALK模型Jeffrey在1990年提出的一种将序列数据化的CGR-WALK方法［6］，其是一种迭代映射技术，可以将蛋白质序列中的每一个位置上氨基酸投影到一个连续坐标空间上，由此将序列进行可视化图形表示，同时可以进行有效的进行独立的精确尺度的序列分析研究。

在详细的HP模型中将20种氨基酸分成4大类，即非极性氨基酸（non-polar），极性带负电荷的氨基酸 （negative polar），极性不带电荷的氨基酸（uncharged polar），极性带正电荷的氨基酸（positive polar），在此分别记作NP，NEP，UP，PP。因此将20种氨基酸｛A，I，L，M，F，P，W，V，N，C，Q，G，S，T，Y，D，E，R，H，K｝按照在详细的HP格点模型中依据氨基酸的生物特性的分类方法将氨基酸依次分类：

NP=｛A，V，L，I，P，F，W，M｝，NEP=｛D，E｝，UP= ｛G，S，T，C，Y，N，Q｝，PP=｛K，R，H｝。

经过分类之后，则可将任意含有n个氨基酸的蛋白质序列进行数据化定义：蛋白质序列 s=s1s2s3…sn，其中si，i=1，2，…，n为组成此蛋白质序列的氨基酸，

由上方法即可将任意一条蛋白质序列转化为一条由A0，A1，A2，A3构成的四元序列，记作：X（s）= α1α2α3…αn。

定义序列X（s）的CGR-WALK：

（1）在二维坐标平面上作［0，1］×［0，1］正方形，标记四个顶点为A0（0，0），A1（0，1），A2（1，1），A3（1，0）。

（2）以正方形中心（0.5，0.5）作为CGR-WALK的初始点。

（3）设置目标蛋白质序列的第一个数据作为当前迭代目标，并将初始点与当前起始目标坐标连线，并标记此线段中点。

（4）以此规律依次迭代，继续以蛋白质序列的下一个数据作为当前迭代目标，循环执行（3）过程，直到将整条蛋白质序列循环运算结束，最终得到在坐标平面上的一个可视化CGR-WALK模型视图。

在此给出CGR迭代函数公式：含有n个氨基酸的蛋白质序列：s=s1s2s3…sn，其中si，i=1，2，…，n，并且有si∈｛A，V，L，I，P，F，W，M，D，E，G，S，T，C，Y，N，Q，K，R，H｝，由详细的HP模型的分类得由A0，A1，A2，A3构成的序列：X（s）=α1α2α3…αn。通过以下迭代过程得到此蛋白质序列的CGR：令A0（0，0），A1（0，1），A2（1，1），A3（1，0），即：

CGRi=CGRi-1-0.5（CGRi-1-gi），i=1，2，…N，CGRi= （0.5，0.5）。

其中gi∈｛（0，0），（1，0），（1，1），（0，1）｝，gi与si相对应。

对于流感病毒的蛋白质序列研究，在此定义变量tk=yk/xk，其中xk和yk分别是CGRk的x和y对应坐标值，由此可以将甲型H1N1流感病毒蛋白质序列数据化为一条具有统计意义的数据序列 ｛tk：k= 1，2，…，n｝，即视作一条时间序列，由于其是经过CGR-WALK得到，则在此记为“CGR-WALK序列”。

1.2.2ARFIMA模型定义1｛εt｝为白噪声序列［7］，记作εt～WN（μ，σ2）。如果时间序列满足如下性质：

（1）任取t∈T，有Eεt=u；

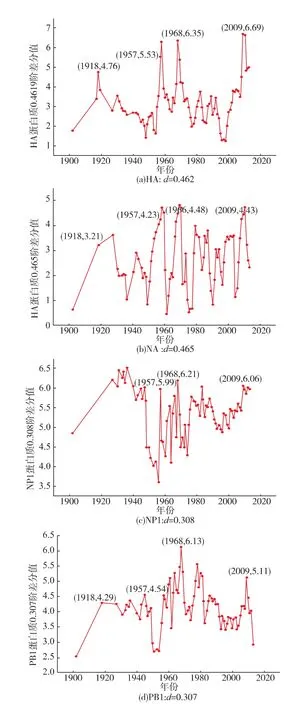
图1　蛋白质HA，NA，NP1，PB1差分时序图Fig.1　Differenced model of HA，NA，NP1，PB1 sequence tim ing diagram

定义 2如果随机序列｛Xt｝满足差分方程（1-B）dxt=εt，其中 -0.5＜d＜0.5，｛εt｝为白噪声序列，Eεt=0，E=σε2＜∞，称｛Xt｝服从-0.5＜d＜0.5的ARFIMA（0，d，0）模型［7］。

定义3如果随机过程｛Xt｝是平稳的，且满足差分方程Φ（B）▽dxt=Θ（B）εt，其中｛εt｝为白噪声序列，Eεt=0，E=＜∞，Θ（B）=1-Φ1B-…-ΦpBp，为 p阶自回归系数多项式；Θ（B）=1-θ1B-…-θqBq，为q阶移动平均系数多项式，-0.5＜d＜0.5，则称｛Xt｝服从-0.5＜d＜0.5的ARFIMA（p，d，q）模型［8］。

2　结果与分析

2.1流感病毒蛋白质序列数据集构造

选取数据库中1902—2013年的所有关于流感病毒蛋白质序列，对所取的数据集中每一条序列从第一个位置开始，进行数据化处理，即将A0→0；A1→1；A2→2；A3→3。则可将由初始的氨基酸序列转化为由0，1，2，3构成的四元序列，并对序列进行CGR-WALK转化，获得CGR-WALK后的｛tk｝数据集。在此对每种蛋白质对应的t值序列分别求其变异系数，得到10组相应蛋白质的变异系数数据集。

2.2甲型H 1N1流感病毒蛋白质数据集特征分析

以流感病毒蛋白质HA、NA、NP1、PB1（分别为Hemagglutinin，Neuraminidase，Nonstructural Protein 1，Polymerase PB1等4种蛋白简写）为例进行分析。计算得其差分值分别为：d1=0.462，d2=0.465，d3=0.308，d4=0.307。

对应其di（i=1，2…，10）阶差分分别得到4组对应的差分序列。然后分别作对应阶差分的时间序列图（如图1），可以看到在从所选择数据中4次爆发年份1918，1957，1968，2009年所对应差分值较高，此数据结构与实际情况相符。

在图2中分别做了关于4种蛋白对应阶差分值的自相关函数（ACF）和偏自相关函数（PACF）图像，可以发现他们的自相关函数曲线衰减迅速，偏相关函数曲线衰减缓慢，则其具备长记忆的特征。

对4种蛋白质对应的差分序列进行白噪声检验，（结果见表1），均有P＜0.000 1＜0.05，则可知它们不是白噪声序列，则可利用ARFIMA（p，d，q）模型对4组序列进行拟合。

由Akaike信息判别准则，选取ARFIMA（1，-0.047，1），ARFIMA（4，0.308，0），ARFIMA（2，-0.146，0），ARFIMA（2，0.307，3）对4条序列进行拟合，在表2中给出模型中相应的参数估计值。从表中可以看到，P值都小于0.1，则表明ARFIMA（p，d，q）模型的对序列能够取得很好的拟合效果。

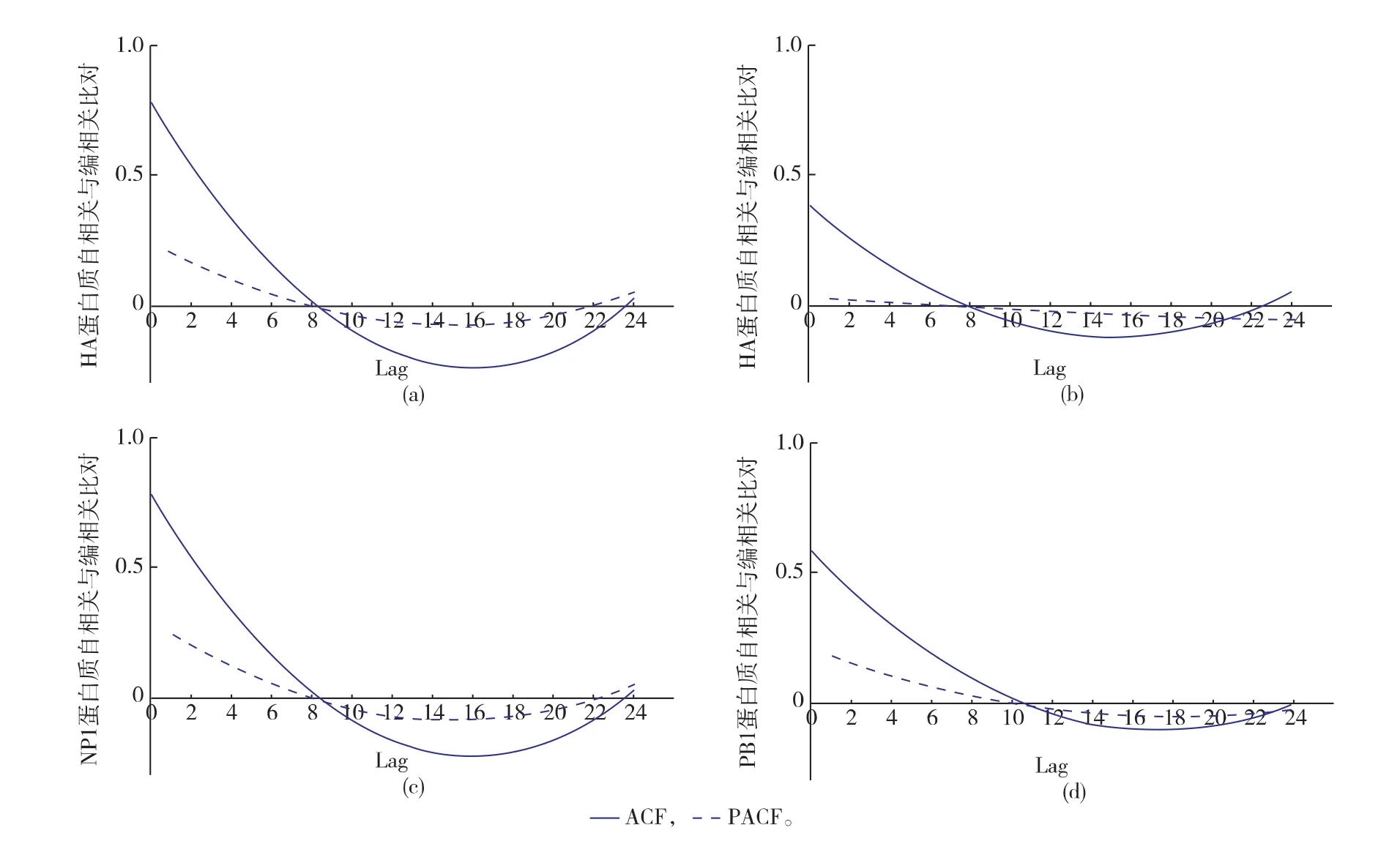
图2　蛋白质HA、NA、NP1、PB1的ACF与PACF曲线图Fig.2　ACF and PACF of HA、NA、NP1、PB1

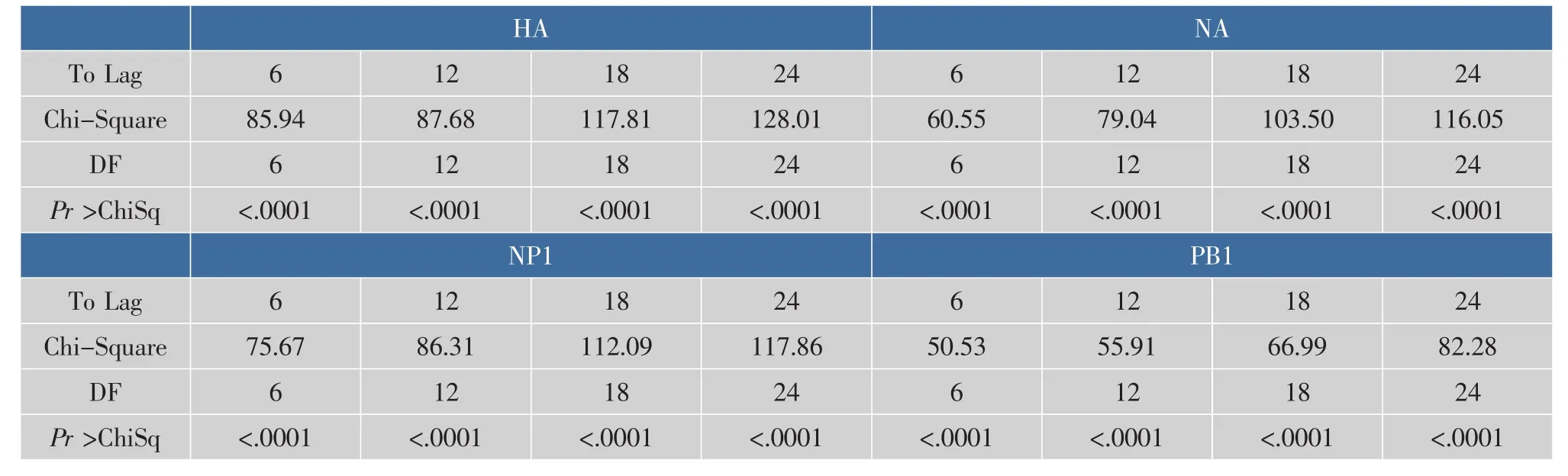
表1　蛋白质HA、NA、NP1、PB1的白噪声检验Table 1　W hite noise test of HA、NA、NP1、PB1

最后对模型的合理性进行检验，选取LB检验统计量：

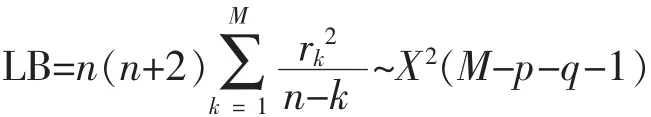
其中rk是滞后的样本自相关函数，n为样本容量，M是一个比n小的常数，且n为正整数。

由此可得表3中为各滞后阶数的相关统计量，其中LB统计量的P值都显著大于0.1，则可知所拟合模型的残差序列为白噪声序列，则ARFIMA（p，d，q）模型可以进行正确的数据拟合，即此模型在流感病毒蛋白质序列分析是合理的。

在表4中给出由ARFIMA（p，d，q）模型进行流感病毒4种组成蛋白在未来10年中的趋势预测。并从对应图3中的预测图中综合观察，自1902年起到未来10年中关于4种流感病毒组成蛋白HA、NA、NP1、PB1的变化趋势。在1918，1957，1968，2009年4次流感爆发年份中，在图中都有大幅度的波动，表明该模型的建立符合实际情况。从2014—2023这未来10年中波动情况存在差异，蛋白质HA 与NP1较平缓，蛋白质NA与PB1有明显起伏，因此在未来十年里要对蛋白质NA与PB1的变异情况进行重点的研究和检测，为流感病毒预防和临床治疗提供指导与帮助。

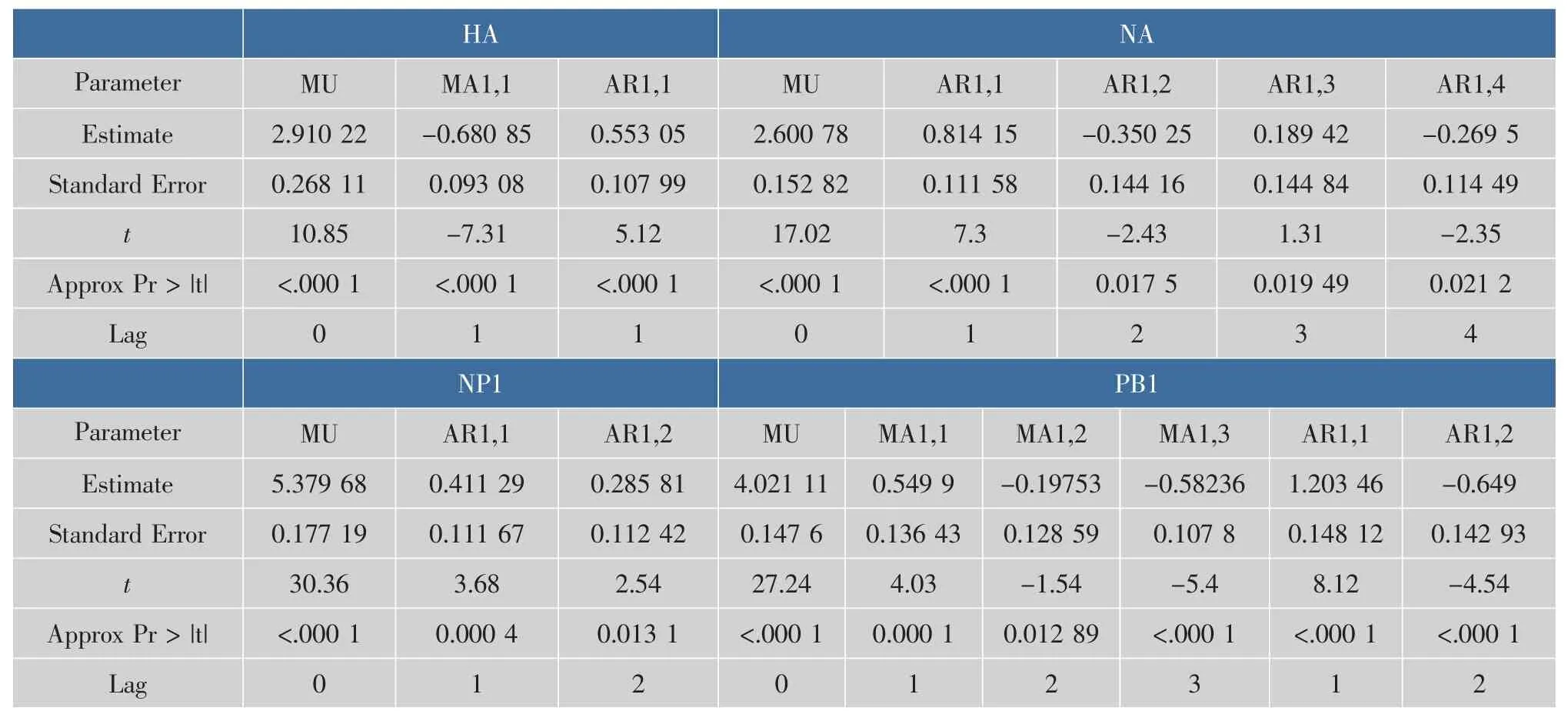
表2　蛋白质HA、NA、NP1、PB1的参数的最小二乘估计Table 2　Least-square estimation of HA、NA、NP1 and PB1

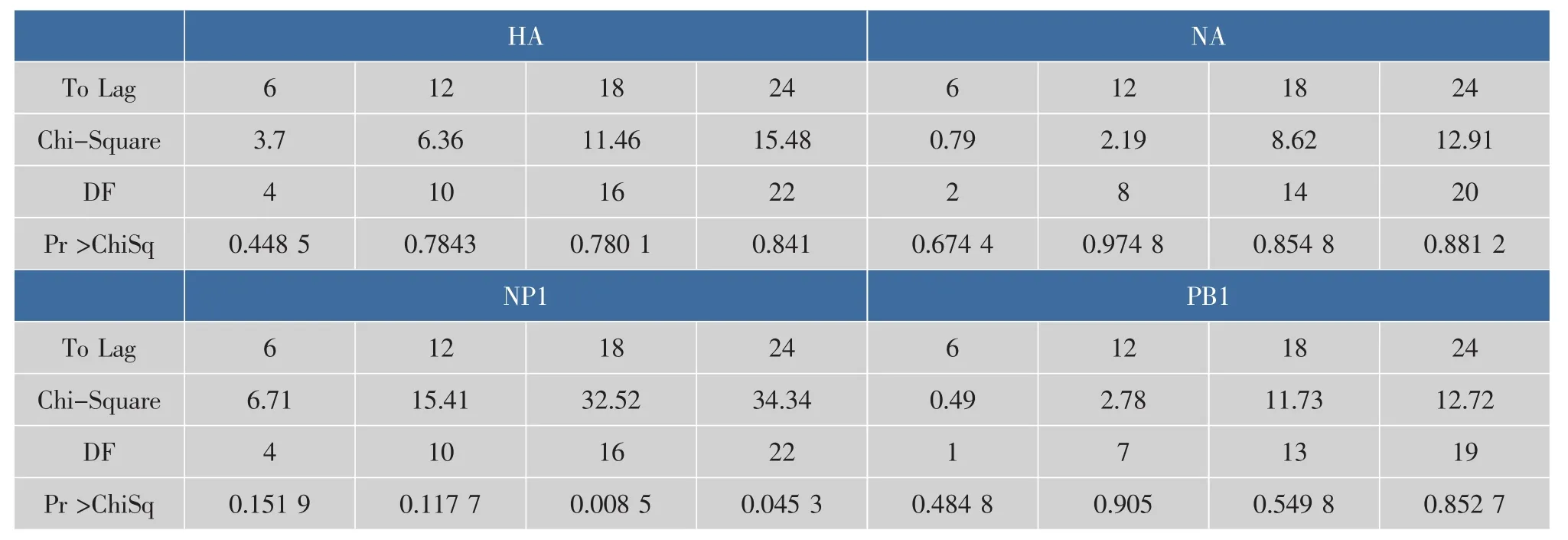
表3　蛋白质HA、NA、NP1、PB1的参数的自相关检验Table 3　Auto-correlation test of the HA、NA、NP1 and PB1

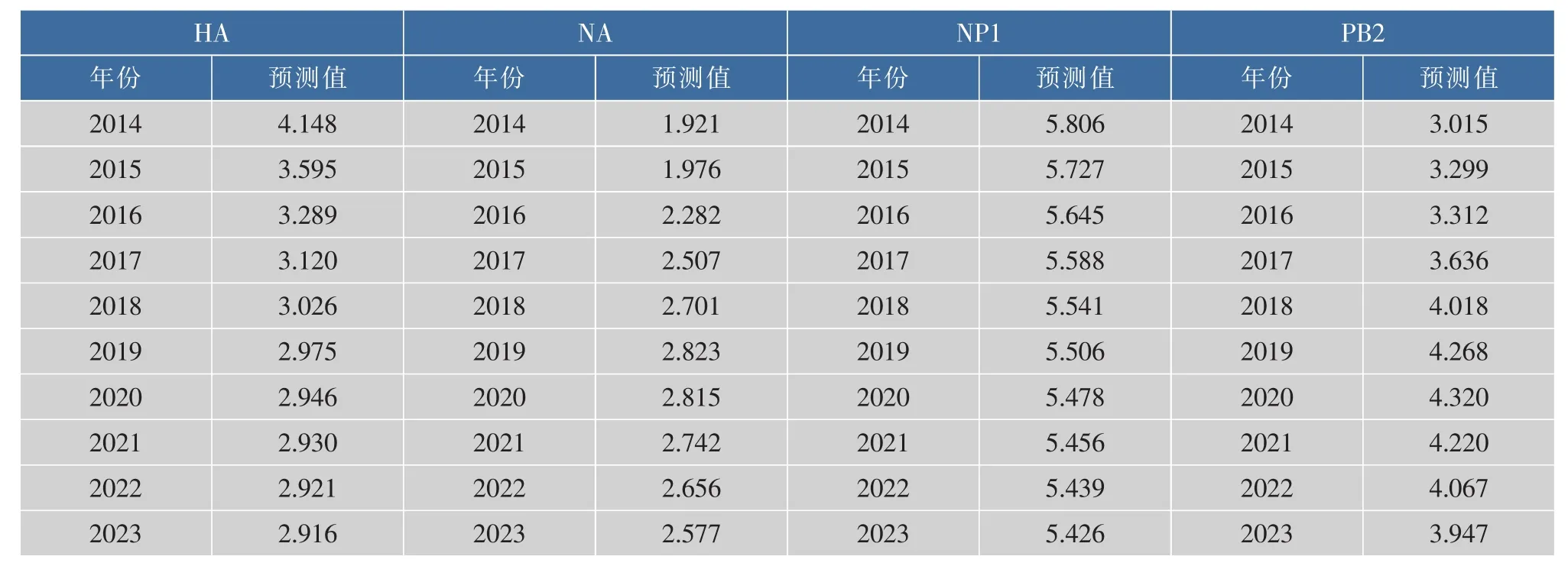
表4　蛋白质HA、NA、NP1、PB1在未来10年中的预测值Table 4　Forest values of HA、NA、NP1 and PB1

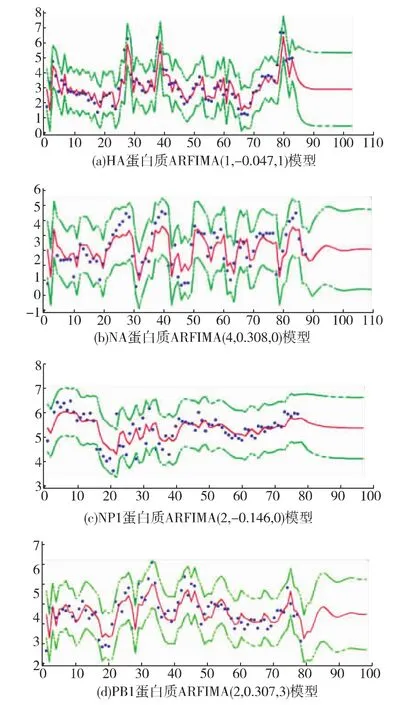
图3　蛋白质HA、NA、NP1、PB1差分时序模型与预测图Fig.3　Forestmodel of HA、NA、NP1、PB1

3　结语

利用大数据分析处理方法获得所要研究的对象，并利用详细的HP模型将全部蛋白质序列数据化，以CGR-WALK模型和分数阶差分模型对目标数据进行处理，最终求的相应的变异系数序列，分析后显示其具有明显的长记忆特征，并对相应序列的差分化序列运用ARFIMA（p，d，q）模型对其进行预测，从理论上取得了较好的预测分析结果；又由预测结果可知，利用从1902—2013年流感病毒的10种组成蛋白的氨基酸序列数据得到的时间序列模型结果很好的与历史上4次较大流感爆发年份1918，1957，1968，2009相吻合，并接着进行了2014—2023年序列的变异情况进行预测，从理论和实际分析应用中表明时间序列分析结合大数据的思想对流感病毒蛋白质序列的分析预测有重要的应用和研究意义，由此表明最终获得很好的预测效果，在下一步的研究中要进一步完善数据收集和整理工作，以更加全面的数据作为研究分析工作的基础，并对模型在精确度上进行优化，提高该研究的实际应用价值和科研价值。

［1］Hilleman，MauriceR.Realities and enigmas of human viral influenza：pathogenesis，epidem iology and control［J］.Vaccine，2002，20（25-26）：3068-3087.

［2］刘娟，高洁.甲型流感病毒DNA序列的长记忆ARFIMA模型［J］.物理学报，2011，60（4）：702-707. LIU Juan，GAO Jie.Long-memory ARFIMAmodel for DNA sequencesof influenza A virus［J］.Acta Physica Sinica，2011，60 （4）：702-707.（in Chinese）

［3］刘娟，高洁.甲型H1N1流感病毒DNA序列碱基的预测［J］.生物信息学，2011，9（3）：259-262. LIU Juan，GAO Jie.Forecasting bases for DNA sequences of influenza virus A/H1N1［J］.China Journal of Bioinformatics，2011，9（3）：259-262.（in Chinese）

［4］刘娟，高洁.乙型、丙型流感病毒DNA序列的长记忆ARFIMA模型［J］.生物信息学，2011，9（2）：97-101. LIU Juan，GAO Jie.Long-memory ARFIMA model for DNA sequences of influenza B，C virus［J］.China Journal of Bioinformatics，2011，9（2）：97-101.（in Chinese）

［5］刘娟.基于时间序列理论方法的流感病毒DNA序列特征分析［D］.无锡：江南大学，2011.

［6］Jeffrey H J.Chaosgame representation ofgene structure［J］.Nucleic Acids Research，1990，18（8）：2163-2170.

［7］王燕.应用时间序列分析［M］.北京：中国人民大学出版社，2008.

［8］GAO Jie，XU Zhenyuan.Chao game representation（CGR）-walk model for DNA sequences［J］.Chinese Physics B，2009，18 （11）：370-376.

Sequence Analysis and Prediction of the Influenza Virus Protein

JIN Peixuan，GAO Jie*
（School of Science，Jiangnan University，Wuxi214122，China）

Ten protein am ino acid sequences of influenza virus were obtained from the National Center for Biotechnology Information（NCBI）from 1902 to 2013，which was analyzed using big data in MATLAB programm ingw ith the detailed HPmodel.Meanwhile，the protein sequenceswere converted to the data series based on the CGR-WALK model.The time series ARFIMA（p，d，q）was introduced to fit all the sequences.The analysis results indicated a good model w ith accurate prediction for the variation tendency in the next 10 years，which also provided a reference for the prediction of influenza virususing thebig dataanalysis.

influenza virus，protein sequence，the detail HPmodel，CGR-WALK model，ARFIMA （p，d，q）model

Q 51

A

1673—1689（2016）04—0393—06

2014-06-09

国家自然科学基金项目（11271163）；中央高校基本科研业务费专项资金项目（JUSRP21117）。

高洁（1972—），女，江苏无锡人，工学博士，副教授，主要从事生物信息学研究。E-mail：ezhun6669@sina.com