加筋板结构连续焊焊接变形规律

陈哲超，陈震

上海交通大学船舶海洋与建筑工程学院，上海200240

加筋板结构连续焊焊接变形规律

陈哲超，陈震

上海交通大学船舶海洋与建筑工程学院，上海200240

基于通用有限元软件Abaqus，采用顺序耦合热弹塑性有限元方法对加筋板结构双边连续焊焊接变形规律进行了研究。为了提高计算效率，采用具有截面积分特性shell单元的shell/solid模型描述加筋板结构，实现了焊接过程数值模拟。针对双边连续焊焊接方式，分别计算比较了T形接头两侧同时焊接和两侧依次焊接情况下的结构残余变形和应力。结果表明：T形接头两侧同时焊接产生较小的焊接变形，并且变形较为对称。关键词：加筋板；shell/solid模型；同时焊接；依次焊接；焊接变形

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.tj.20160531.1104.024.html期刊网址：www.ship-research.com

引用格式：陈哲超，陈震.加筋板结构连续焊焊接变形规律［J］.中国舰船研究，2016，11（3）：68-73，88.

CHEN Zhechao，CHEN Zhen.Deformation rules of stiffened plates with continuous welding［J］.Chinese Journal of Ship Research，2016，11（3）：68-73，88.

0　引　言

焊接工艺被广泛地应用于船舶与海洋结构物的建造中，焊接质量的高低将直接影响船体生产质量与效率。在焊接过程中，焊缝区域的局部高温加热和冷却造成焊件受热不均，使得结构产生残余变形。焊接残余变形的存在造成结构物外观改变，尺寸精度下降以及承载能力减弱。在焊接过程中，采用合理的焊接工艺有利于减少残余变形，提高焊接质量。

热弹塑性有限元方法［1-2］是研究结构焊接温度场、焊接变形和残余应力的有效方法，成功地应用于各种典型接头的焊接数值模拟中。本文采用顺序耦合的热弹塑性有限元分析方法，利用Abaqus非线性有限元软件，对船体典型加筋板结构焊接变形规律进行研究。为了提高计算效率，采用Shell/Solid模型建立结构有限元模型，计算并比较了加强筋T形接头两侧同时焊接和两侧依次焊接情况下的焊接变形和残余应力。

1　数值分析原理

1.1顺序耦合热弹塑性有限元

顺序耦合热弹塑性有限元方法假定焊接过程中材料的力学响应对温度场的影响较小，可以忽略不计，仅考虑温度场对应力场的影响。分析分为2个步骤：首先进行焊接过程热传导分析，获得温度场结果；然后将温度场的结果作为外载荷施加到力学模型，计算得到焊接变形和残余应力。

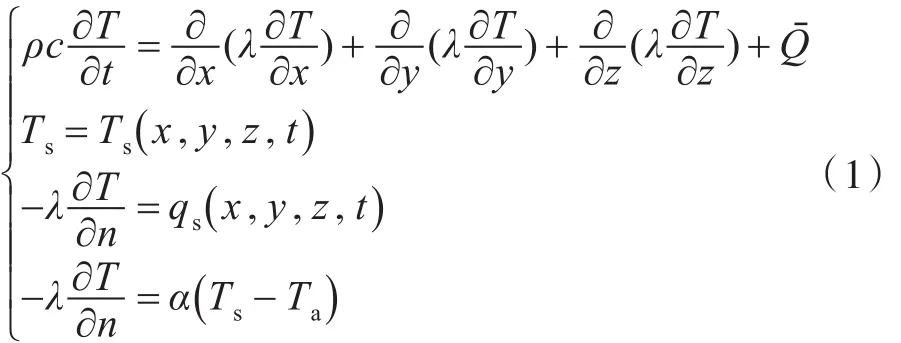
热传导分析控制方程及边界条件［2］为：式中：T为瞬时温度；c为比热；ρ为密度；λ为导热系数；Q为内热源；Ts为边界温度；qs为热流；Ta为环境温度；α为对流换热系数。

应力场分析采用塑性增量理论，弹塑性应变公式［2］为

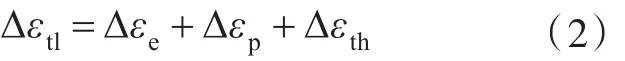
式中：Δεtl为总应变增量；Δεe为弹性应变增量；Δεp为塑性应变增量；Δεth为热应变增量。

弹性应变增量遵循广义胡克定律计算，热应变增量根据线膨胀系数进行计算，塑性变形遵循Von Mises屈服准则以及相关的流动性准则，所涉及到的各材料物理特性均考虑随温度的变化。

1.2Shell/Solid模型

采用Solid单元的热弹塑性有限元方法建模过程繁琐，计算量大，难以实现大型结构的焊接过程模拟。本文采用具有截面积分特性的Shell单元和Shell/Solid模型方法［3］，有效地提高了计算效率。

具有截面积分特性的Shell单元可在单元节点处设置沿厚度方向的积分点。在热传导分析过程中，积分点具有独立的温度自由度，节点温度值存储为相应积分点的温度序列。对于Shell单元中任意一点的温度值，由单元形函数和积分点处的温度值插值求得

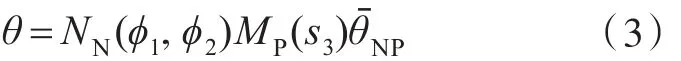
式中：NN（ϕ1，ϕ2）为单元参考面内的插值函数；MP（s3）为沿厚度方向的二次分段插值函数；θ¯NP为积分点处的温度值。

在Shell/Solid模型中，焊脚采用Solid单元模拟，焊接板材采用Shell单元模拟。为了反映板材和焊脚之间接触面上温度场和应力场的连续性，在相应位置利用约束方程绑定相应温度和力学自由度。本文利用Python语言编写Abaqus脚本程序［4］，实现各自由度的自动绑定。

2　分析模型

2.1研究内容

本文的研究对象为船体结构中典型的加筋板结构。加筋板结构由外板、5根纵向加强筋和2根横向加强筋组成。外板尺寸为2 400 mm×1 920 mm× 8 mm；纵向加强筋沿外板宽度方向等距离布置，间距480 mm，加强筋尺寸为100 mm×8 mm；横向加强筋间距960 mm，尺寸为180 mm×8 mm。焊接时采用CO2气体保护焊，仅对纵向加强筋焊接过程进行模拟。模型几何参数及焊接顺序如图1所示［5］。

图1　板格模型及焊接顺序Fig.1　Stiffened plate model and welding sequence

对于纵向加强筋的焊接，本文分别对T形接头左右两道焊缝依次焊接和同时焊接这2种焊接方式进行模拟，研究2种焊接方式下焊接变形和残余应力的规律和特点。采用依次焊接时，对于加强筋的两侧焊缝，先进行左侧焊缝焊接，后进行右侧焊缝焊接；采用同时焊接时，对于加强筋的两侧焊缝，左右侧焊缝同时进行焊接，如图2所示。焊接参数如表1所示。

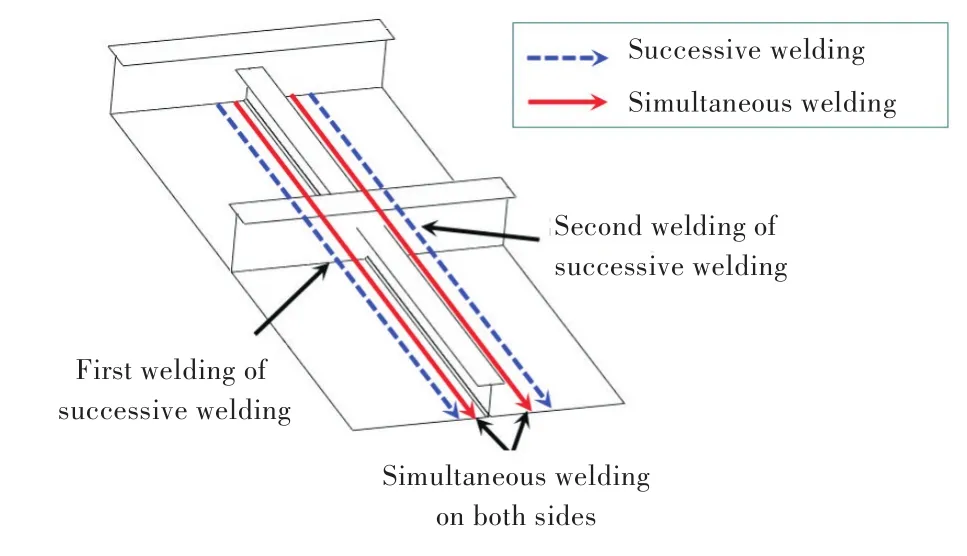
图2　T形接头两侧依次焊接与同时焊接Fig.2　Successive and simultaneous welding of the T-joint model

表1　焊接参数Tab.1　Parameters of welding

2.2计算模型

加筋板结构有限元模型利用Shell/Solid模型建立。在热传导分析计算模型中，船体板和加强筋采用Shell单元建立，单元类型为DS4，焊脚采用Solid单元建立，单元类型为DC3D8［6］。Shell单元沿厚度方向设置5个积分点，以准确描述温度梯度沿板厚的分布情况。在应力场计算中，结构有限元模型几何尺寸与网格划分同温度场中模型保持一致，船体板与加强筋采用Shell单元建立，单元类型为S4。

在焊接模拟过程中，移动热源造成焊缝线附近区域温度梯度急剧变化，而较远区域的温度受热源的影响很小，因而在温度场计算中可以忽略离焊缝线较远的区域。在温度场计算中，如果采用整体板架模型进行计算，求解自由度数量庞大。为了提高计算效率，焊接温度场的计算采用子结构方法。将加筋板结构划分为5个加筋板子结构，每个子结构包含一条加强筋及附近区域（图3）。当前加强筋焊接时只计算相应子结构温度场模型。

图3　模型子结构划分Fig.3　Substructure of the model

结构分析模型采用完整加筋板结构模型，模型一侧横向边缘中间位置采用z向约束，另一侧两端位置分别采用y，z方向约束和x，y，z这3个方向约束。材料采用E36钢，其杨氏模量、热膨胀系数、比热、热传导系数等物理量与温度的关系如图4所示。

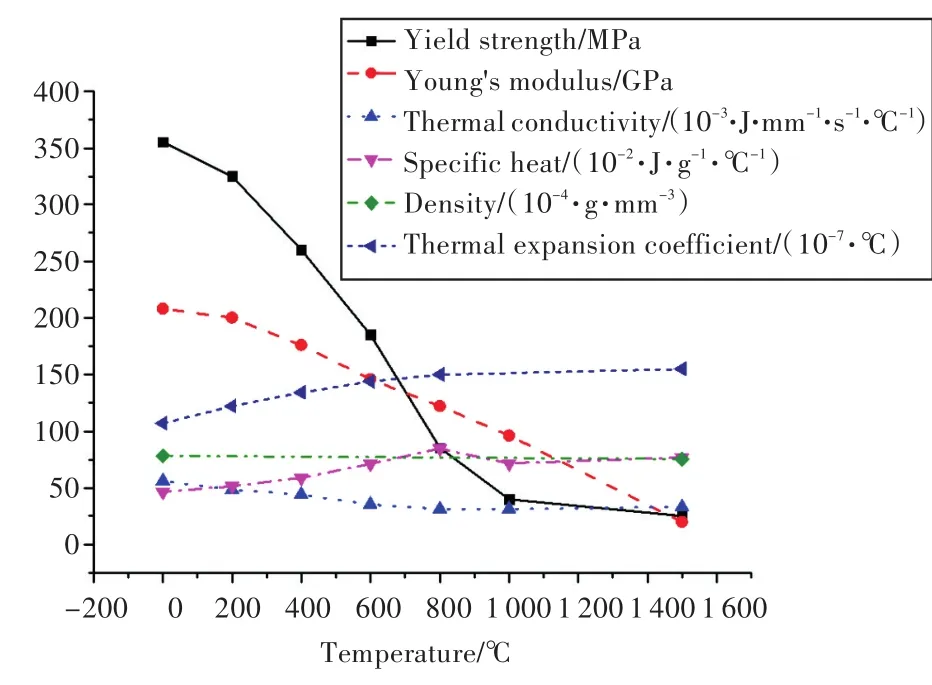
图4　材料属性Fig.4　Material properities

分析中，利用移动热源模拟焊接过程，热输入分为2个部分［7-8］：一部分由焊弧传递至熔池表面，将高斯分布面热源模拟，施加于焊脚与母材交界a）exp［-3（r（t）/ra）2］（4）式中：r（t）为距离焊弧中心点的距离；ra为电弧半径；QG为高斯面热源的总能量，QG=40%.ηUI，η为热输入效率，U与I分别为焊接电压与电流。模拟中所涉及的相应焊接参数如表1所示。面，占总热量输入的40%；一部分由融滴传递至熔池内，采用均匀分布体热源模拟，施加在焊脚上，占总热量输入的60%。高斯平面热源的热流公式为

qG（r）=3QG/（πr2

2.3方法的验证

为了验证Shell/Solid模型和计算方法的准确性，本文针对T形接头［8-9］焊接过程进行模拟（图5）。T形接头焊接实验的焊接板材由9 mm厚腹板与12 mm厚面板组成，腹板底端与面板相交处两侧分别施焊，面板尺寸为500 mm×500 mm，腹板尺寸为300 mm×500 mm。T形接头右侧两端点采用z方向约束，左侧两端点分别采用x，z方向约束及x，y，z方向约束［9-10］。

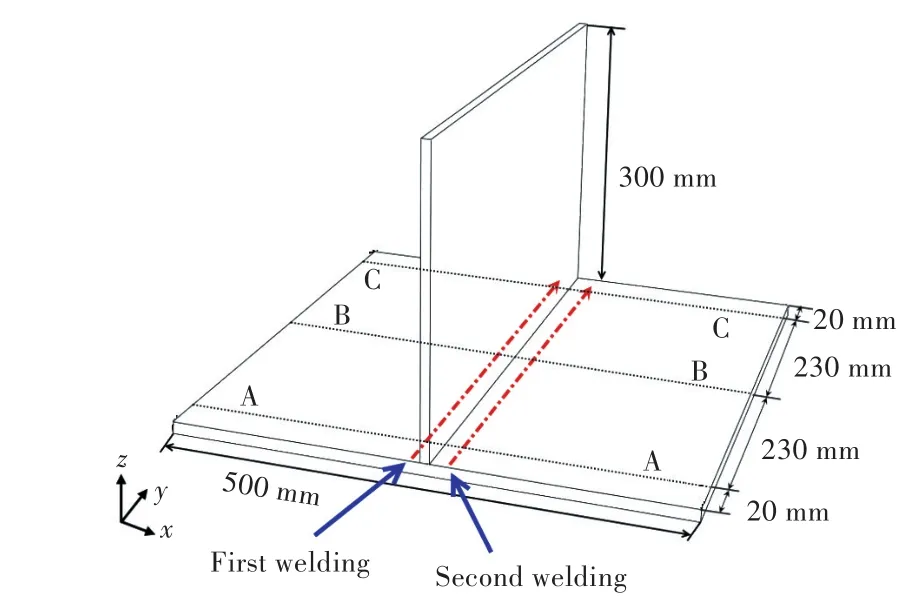
图5　T形接头Fig.5　T-joint model

针对该T型结构建立Shell/Solid模型（图6）进行模拟，并将实验结果和Solid模型（图7）计算结果进行了对比。

图6　Shell/Solid模型Fig.6　Shell/Solid model

图7　Solid模型Fig.7　Solid model

对Shell/Solid模型，考察其热源中心所在横截面温度的分布情况（图8），在焊脚与面板、腹板的接触面上，温度分布连续，同Solid模型横截面温度分布情况几乎一致（图9）。可见自由度绑定程序将接触面上相应位置处的节点与积分点成功实现线性绑定，成功模拟实际情况中的热传导过程。

图8　Shell/Solid模型横截面温度云图Fig.8　Temperature contours at transverse section of Shell/Solid model

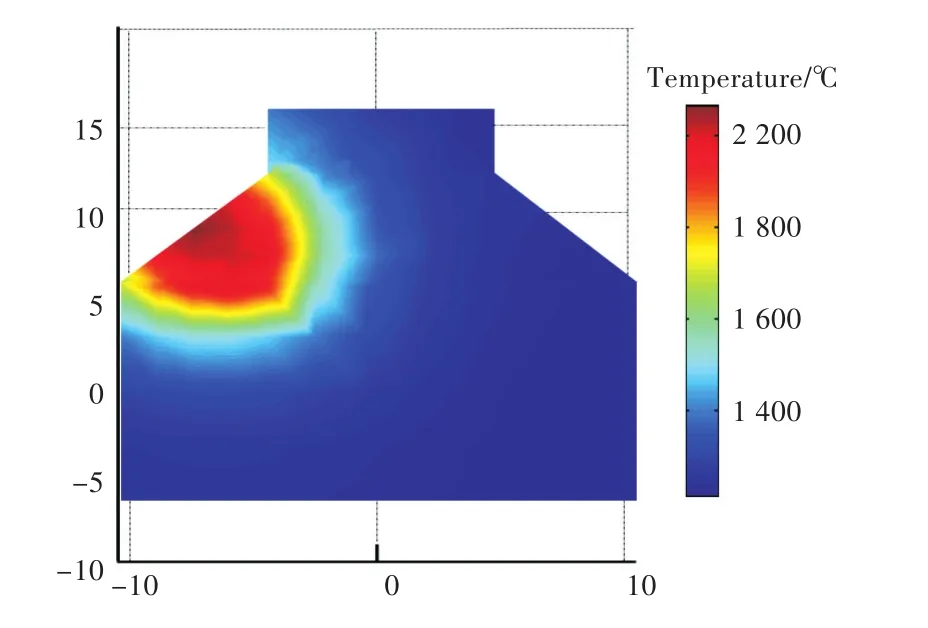
图9　Solid模型横截面温度云图Fig.9　Temperature contours at transverse section of Solid model

考察AA，BB，CC这3条直线处角变形情况（图10），结构产生了明显的角变形。面板边缘处几乎没有变形，焊缝位置处结构下沉，整体呈现V型。直线CC位置角变形最大，AA位置角变形最小。计算结果同实验结果变形趋势一致，Shell/ Solid模型变形数值略大于Solid模型，略小于实验数值。

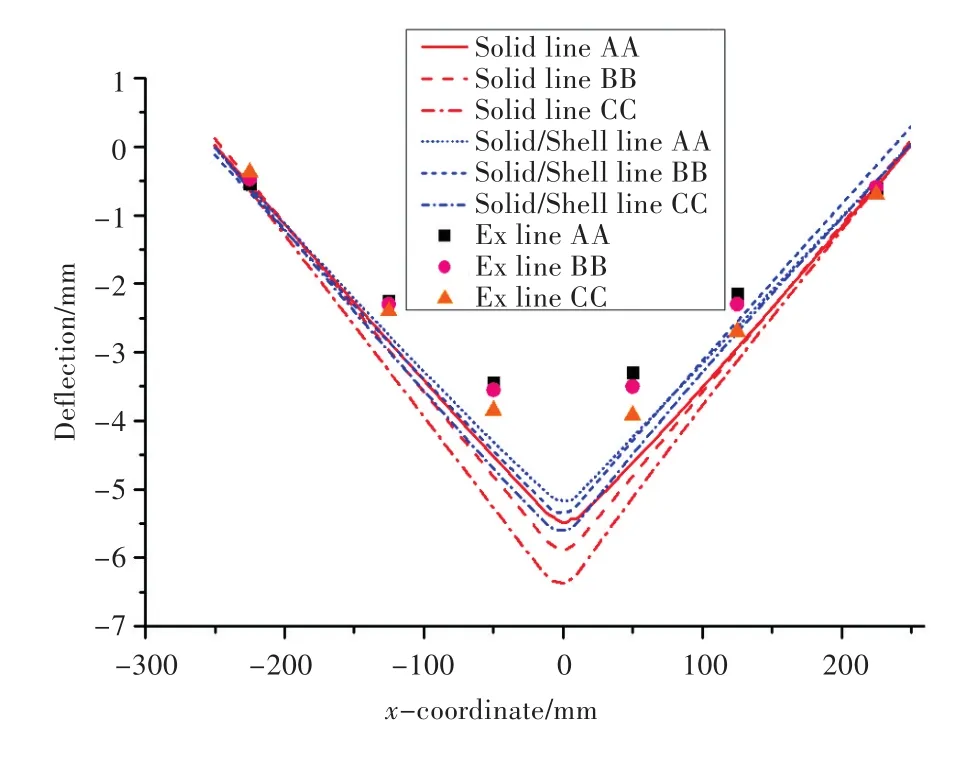
图10　T形接头角变形Fig.10　Angular distortion of T-joint model

Shell/Solid模型计算结果与Solid模型和实验结果较吻合，验证了方法的准确性。

计算在相同的计算机配置下进行，表2对计算耗时进行对比。Shell/Solid模型计算总耗时是Solid模型的50.6%。

表2　计算时间汇总Tab.2　Summary of computational time cost

3　模拟结果

3.1温度场计算结果

在焊接加热过程中，利用移动热源进行焊接热输入模拟。纵向加强筋瞬态温度场模拟结果如图11所示。加热过程中最高温度稳定在2 700℃左右。

T形接头两侧同时焊接焊缝横截面温度分布绘制成二维形式，如图12所示。两侧同时焊接时，左右焊脚温度分布对称，最高温度出现在焊脚斜边中心位置处。两侧依次焊接，首先进行左侧焊缝焊接，再进行右侧焊缝焊接。进行左侧焊缝焊接时焊缝横截面温度分布示意图如图13所示。横截面左侧温度分布情况与同时焊接横截面左侧温度分布大致相同。

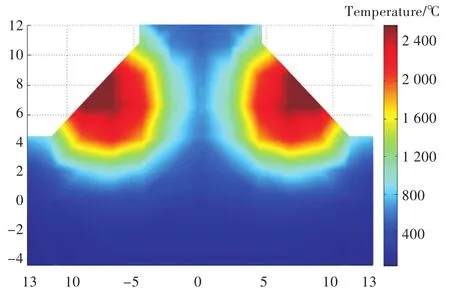
图12　同时焊接横截面温度分布Fig.12　Temperature contours at transverse section of simultaneous welding

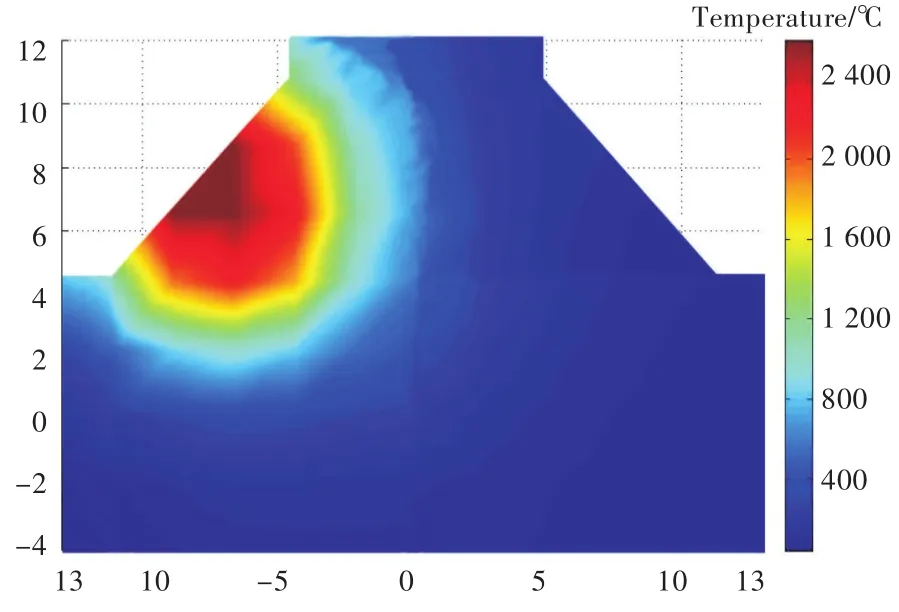
图13　依次焊接横截面温度分布Fig.13　Temperature contours at transverse section of successive welding

3.2焊接变形和应力计算结果

图14为两侧同时焊接完成后加筋板结构垂向变形图。为了更加清楚地了解加筋板结构的焊接变形状况，在模型上设置多道直线，对2种焊接方式各直线所在位置处（图15）的焊接垂向变形及应力情况进行分析。

图14　两侧同时焊接垂向变形云图Fig.14　Vertical distortion of simultaneous welding

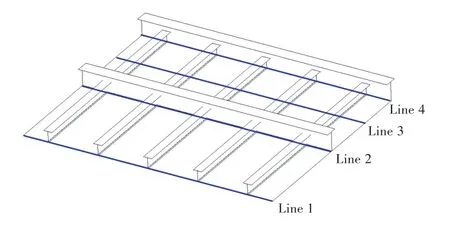
图15　直线位置Fig.15　Position of the lines

加筋板共有5道纵向加强筋，完成第1道中间加强筋焊接模拟后，两侧板架均向上翘起。采用依次焊接的板架左侧变形幅度大于右侧，而采用同时焊接的板架左右两侧变形幅度一致。

第3道加强筋焊接完成后，直线1处焊接变形如图16所示。相邻纵骨间板格变形呈现马鞍形。采用同时焊接方式的板架，完成焊接的第2和第3道加强筋通过变形回到了起始位置，整体变形对称。依次焊接的板架，由于在中间加强筋焊接时板架就呈现左侧变形大，右侧变形小的状态，当完成第3道加强筋焊接时，左侧加强筋位置上移，右侧加强筋位置下移。完成5道加强筋焊接时的变形如图17所示，加筋板依旧保持之前的变形趋势。采用同时焊接方式的板架，由于每一道加强筋焊接造成板架左右两侧的变形都较为对称，整体变形结果对称，并且加强筋所在位置几乎保持在起始位置。而采用依次焊接方式的板架，变形的不对称性不断累加，造成板架总体变形不对称非常明显，两侧加强筋均明显偏离起始位置，左侧变形值最大达到9.8 mm。

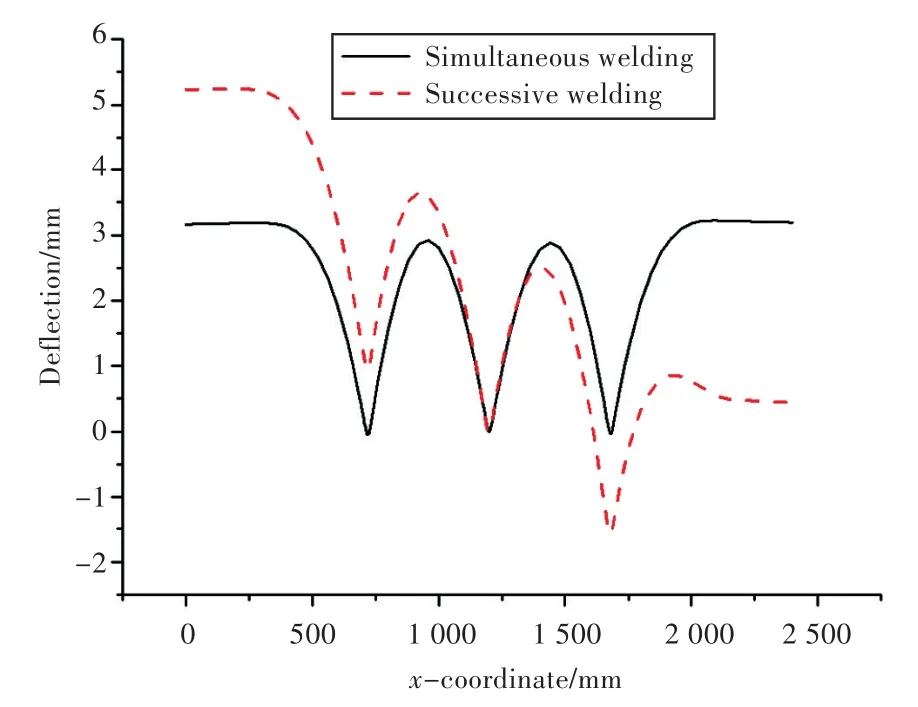
图16　直线1处前3道加强筋完成焊接时的变形Fig.16　Deflection after first 3 stiffeners accomplishing welding on line 1

图17　直线1处5道加强筋完成焊接时的变形Fig.17　Deflection after 5 stiffeners accomplishing welding on line 1

图18反映了焊接完成时直线2处的垂向变形。直线2位于加筋板中间横向加强筋处。采用同时焊接的板架模型在中间拱起，变形最大达到2.7 mm，两侧变形较小，为0.8 mm。依次焊接的板架左侧变形最大，达到3 mm，向右变形逐渐减小。

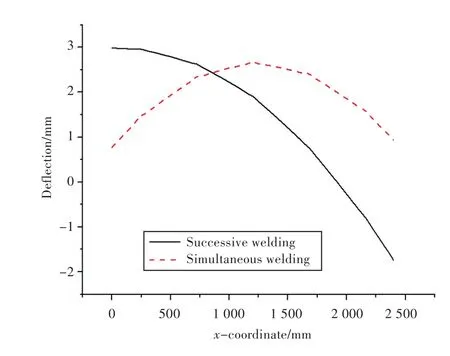
图18　直线2处变形Fig.18　Deflection on line 2

图19反映了焊接完成时直线4处的垂向变形。直线4位于加筋板边缘横向加强筋处。加强筋两端约束位置没有变形，中间拱起，采用同时焊接的板架在中间位置处变形1.8 mm，采用依次焊接的板架该处变形1.2 mm。综合以上3处直线位置处的变形，采用依次焊接的板架出现扭曲变形。

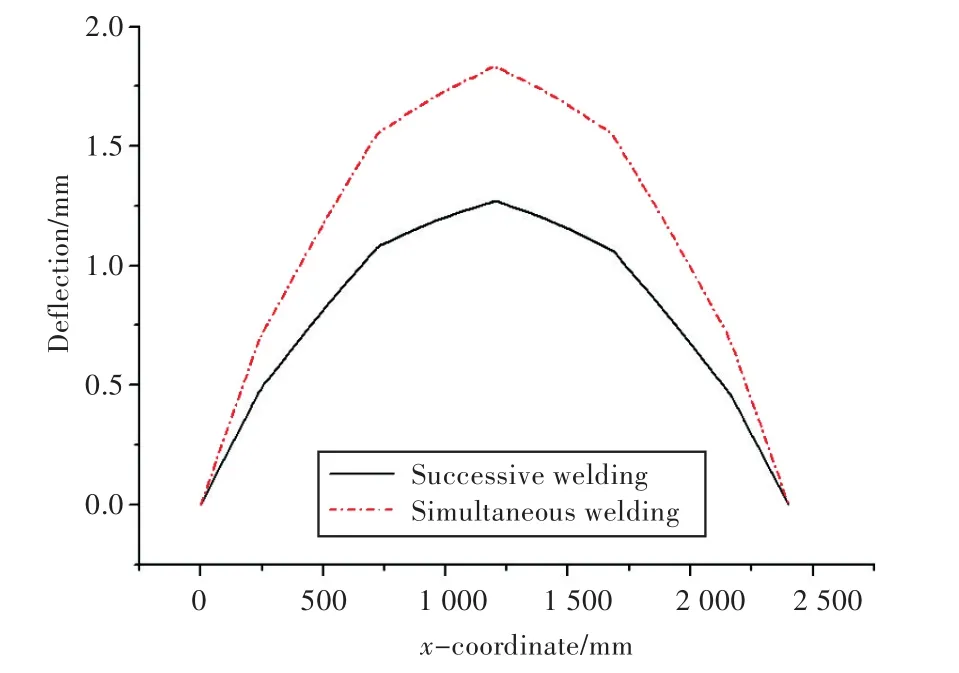
图19　直线4处变形Fig.19　Deflection on line 4

图20为在直线3处，2种焊接方式焊缝方向残余应力对比。在焊缝线附近，残余应力急剧升高，拉应力达到峰值，2种焊接方式残余拉应力极值相近。在加强筋之间的平板区域，拉应力转变为压应力，同时焊接产生的压应力较大。

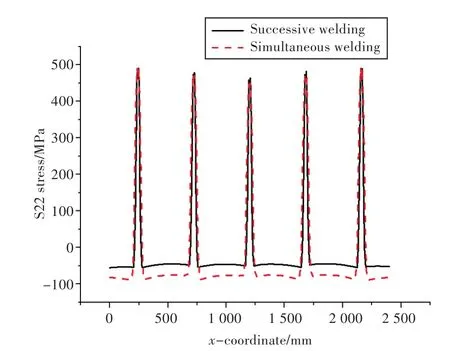
图20　直线3处残余应力Fig.20　Residual stress on line 3

4　结　论

本文比较了加强筋焊接顺序相同的情况下，T形接头左右2道焊缝同时焊接与依次焊接2种焊接方式对于加筋板结构焊接变形和残余应力的影响，得到如下结论：

1）采用依次焊接，板架出现扭曲变形，变形极值较大。

2）采用同时焊接，加强筋变形对称性好，加

强筋所在位置变形幅度很小，该种焊接方式有利于焊接变形的预测与控制。

3）2种焊接方式对加筋板焊接残余应力影响不大。

［1］UEDA Y，YAMAKAWA T.Analysis of thermal elas⁃tic-plastic stress and strain during welding by finite el⁃ement method［J］.Japan Welding Society，1971，2 （2）：90-100.

［2］ 汪建华.焊接数值模拟技术及其应用［M］.上海：上海交通大学出版社，2003.

［3］SHEN J C，CHEN Z.Welding simulation of filletwelded joint using shell elements with section integra⁃tion［J］.Journal of Materials Processing Technology，2014，214（11）：2529-2536.

［4］曹金凤，王旭春，孔亮.Python语言在Abaqus中的应用［M］.北京：机械工业出版社，2014.

［5］黎超文，王勇，韩涛.焊接顺序对T形接头残余应力和变形的影响［J］.焊接学报，2011，32（10）：37-40.

LI Chaowen，WANG Yong，HAN Tao.Effect of weld⁃ing sequences on welding residual stress and distortion of T-joint［J］.Transactions of the China Welding Insti⁃ tution，2011，32（10）：37-40.

［6］ 赵晟，陈震，罗宇.高阶单元在焊接热弹塑性有限元分析中的应用［J］.焊接学报，2014，35（1）：54-58.

ZHAO Sheng，CHEN Zhen，LUO Yu.Application of high order elements in welding thermal elastic-plastic finite element analysis［J］.Transactions of the China Welding Institution，2014，35（1）：54-58.

［7］ 莫春立，于少飞，钱百年，等.焊接热源计算模式的研究进展［J］.焊接学报，2001，22（3）：93-96.

MO Chunli，YU Shaofei，QIAN Bainian，et al.The de⁃velopment of models about welding heat sources'calcu⁃lation［J］.Transactions of the China Welding Institu⁃tion，2001，22（3）：93-96.

［8］ DENG D A，LIANG W，MURAKAWA H.Determina⁃tion of welding deformation in fillet-welded joint by means of numerical simulation and comparison with ex⁃perimental measurements［J］.Journal of Materials Pro⁃cessing Technology，2007，183（2/3）：219-225.

［9］毕艳霞.T型接头焊接温度场与应力场的数值模拟［D］.杭州：浙江大学，2007.

［10］FU G M，LOURENCO M I，DUAN M，et al.Effect of boundary conditions on residual stress and distor⁃tion in T-joint welds［J］.Journal of Constructional Steel Research，2014，102：121-135.

Deformation rules of stiffened plates with continuous welding

CHEN Zhechao，CHEN Zhen
School of Naval Architecture，Ocean and Civil Engineering，Shanghai Jiao Tong University，Shanghai 200240，China

The welding induced deformation of stiffened plates is investigated in this paper with the thermal elastic plastic FE method.In order to improve the calculation efficiency，shell elements with sec⁃tion integration are adopted to establish the shell/solid model.Two welding methods are studied respective⁃ly in this paper，and several conclusions are drawn after comparing the calculation results.It is observed that simultaneous welding on two sides of the stiffeners could lead to a better deformation mode of the stiff⁃ened plate，which is less significant and shows better symmetry，compared to that of successive welding.

stiffened plate；shell/solid model；simultaneous welding；successive welding；welding in⁃duced deformation

U671.8

A

10.3969/j.issn.1673-3185.2016.03.012

2015-08-04网络出版时间：2016-5-31 11:04

陈哲超，男，1989年生，硕士生。研究方向：船舶与海洋工程结构焊接模拟。

E-mail：czc5478@126.com

陈震（通信作者），男，1976年生，博士，副教授。研究方向：船舶与海洋工程现代强度理论。

E-mail：chenzhen@sjtu.edu.cn