期货上市前后上证50指数特性变化研究

徐 棣，胡 昊

（1.建行阜阳市分行，安徽 阜阳 236010；2.阜阳师范学院 经济学院，安徽 阜阳236037）

期货上市前后上证50指数特性变化研究

徐 棣1*，胡 昊2

（1.建行阜阳市分行，安徽 阜阳 236010；2.阜阳师范学院 经济学院，安徽 阜阳236037）

2015年4月16日，上证50股指期货在中国金融期货交易所正式挂牌交易。股指期货推出近一年来，上证50指数特性的变化是研究的重点。选用Box—Jenkins模型，对期货推出前后股指复合收益率的统计特性、变动趋势及波动率进行分析与描述。研究表明：股指期货的推出未对现货市场造成大的冲击。股指期货上市前后，收益率序列均值方程结构未发生显著变化；条件方差模型中描述股指收益率波动性的Beta系数发生下降，说明股指期货的上市对我国股票市场的稳定起到了一定的促进作用。与此同时，股指收益率非对称效应的形成表明我国股票及期货市场的运行仍需要积极有效的监管。

上证50指数；时间序列分析；条件方差；GARCH族模型

DOI：10.14096/j.cnki.cn34-1044/c.2016.04.26

2010年4 月16日，中国首支股指期货——沪深300股指期货合约在中国金融期货交易所正式挂牌交易，这一举措不仅丰富了我国金融市场衍生品交易种类，而且有利于投资者进行套期保值，增加市场的交易量和流动性。伴随着我国金融市场改革的进一步深化，上证50与中证500股指期货合约于2015年4月16日在中国金融期货交易所正式挂牌交易。

本文主要研究的是上证 50股指期货的推出对于现货市场影响的方向和强度。在理论上，股指期货的推出应起到锁定预期收益，促进市场均衡价格形成的作用，但已有的实证结果表明这一影响有正有负。在上证50股指期货合约推出近一年以来，明确其对现货市场的影响，对于评价上证 50股指期货的运营质量和检验政策的有效性是极为重要的，也是本文的研究动机。

1 相关研究综述

关于股指期货上市对股票市场的影响，学术界一般有如下两种观点：一种认为股指期货属于金融期货，不同于商品期货，持有者的投机动机往往要高于保值动机。因此其作为一种杠杆化金融衍生工具会引发市场投机需求，加大现货市场的波动；另一种认为既然股指期货作为一种可以反向操作的金融衍生工具，在市场价格的形成过程中，其便可以促进均衡价格的形成，减缓市场波动。何东桓［1］总结了海外各市场股指期货推出前后现货市场走势，发现股指期货的推出前后现货价格既有可能上涨，也有可能下跌。由于我国金融市场推出股指期货的时间较晚，可供交易的种类也比较有限，所以国内学者对于这一问题的研究结论主要是基于沪深300股指所得出的，而对上证50和中证500股指所进行的研究较少。

国内学者对于沪深300股指期货上市前后现货市场波动的研究可从两个方面划分，一是研究所选取的时间长度，二是描述现货市场波动过程中所采用的指标。杨艳军等［2］选取股指期货上市前后各3个月的1分钟股指变化数据进行研究，但存在所选取的时间段短、样本量小等问题，检验结果说服力不足。曹森、张玉龙等［3］加大了样本容量，选取期货上市前后各300个交易日的股指数据进行了中长期研究；熊熊、韩笑［4］以沪深300股指期货挂牌交易首日为事件日，选取其前后700个交易日进行实证分析，得到股指期货的上市前后股指波动率模型结构并无变化，但却拉低了现货的整体收益率的结论。

国内学者描述股指期货上市对现货市场影响的指标一般有两种，一是CAPM模型中的Beta系数，其描述的是该项资产的系统性风险；二是股指复合收益率，即收益率的波动率。刘振毅［5］和曹森在分析沪深300股指期货推出对现货市场影响中均使用了Beta系数这一指标，但由于选取时间段不同，加之CAMP模型存在投资者对市场存在一致预期性和市场是无摩擦等前提条件，导致二者在关于长期股票指数所存在的系统性风险问题上得出相反的结论。当二者选取股指复合收益率这一指标，并采用能够描述资产非对称收益效应的 GARCH系列模型进行研究时，均得出期货的引入降低了股指收益的整体波动和风险水平这一结论。郦金梁等［6］基于EGARCH模型的实证分析显示，沪深300指数期货的推出后股票复合收益率条件方差下降了40%，同样表明了股指期货的推出降低了现货市场的波动。

2 数据选取和研究方法

2.1样本数据选择

上证50指数，简称上证50，2004年1月2日起由上海证券交易所正式发布。由上海证券市场上成交活跃，流动性好和规模较大的50只股票组成样本股，用来反映上证市场中较具影响力的一批企业的运营状况。本文以上证50股指期货推出前后上证50每日收盘价数据为研究基础，选取2015年4月16日——上证50股指期货挂牌交易的首日为事件日，分别以该交易日前230个交易日（2014/5/8—2015/4/15）的数据为估计窗，同时以该交易日后 230个交易日（2015/4/16—2016/3/31）为事件窗，进行中长期对比分析，旨在研究股指期货的推出对标的指数波动性的影响。以上数据均来源于上海证券交易所（www.sse.com.cn），统计分析所选用的软件为Eviews 7.0。

2.2研究方法

本文拟采用综述中所提到的两种指标对上证50股指波动性进行检验，但考虑CAPM模型的适用性和有效性问题，最终选取国内学者普遍认可的股指复合收益率来刻画其波动性。首先对股指期货推出前后股指复合收益率序列的统计特征进行描述，再进行ADF检验，判定其是否可采用Box—Jenkins模型进行分析。构建自回归移动平均方程，以2015年4月16日为分段点进行Chow转折点检验，考察该模型结构在事件发生前后有无显著变化。为了回答不同时间段内复合收益率序列是否存在条件方差的问题，先对收益率模型的残差进行ARCH-LM检验。若存在ARCH效应，则进一步选取能够刻画这一波动的GARCH族模型对其进行描述，以便深入探讨。

3实证研究的结果与分析

3.1股指期货上市前后上证 50指数的统计特征分析

本文将上证50复合收益率St作为研究变量。设每日收盘指数为Pt，则有

数据的统计特性可以从三个方面进行测度和描述，分别是分布的集中趋势、离散的平均程度和分布的形状。本文选用数学期望、标准差、峰度和偏度4个数字指标对上证50股指复合收益率进行描述。

图1股指期货上市前后股指复合收益率统计特征

由统计信息图可以看出：在股指期货挂牌交易前后，上证50股指复合收益率的分布相对于正态分布，都呈现出明显尖峰分布。相比之下，期货上市后上证50股指复合收益率尖峰较低，表明在这一时间段内出现极端收益的可能性降低。偏态分布方面，两时段内偏态系数的绝对值均处于0.5到1之间，属于中等偏态分布。股指期货上市后收益率序列｛St｝的均值为-0.000701，较股指上市前的0.001405有明显的下降，这表明现货市场的盈利能力降低；事件日后股指复合收益率的标准差为0.026067，较之前略有提升。复合收益率序列的Jarque-Bera统计量p值均小于0.05，表明其并不服从正态分布，这与Engle［7］等研究结果相一致。

3.2股指复合收益率时间序列变动趋势分析

3.2.1复合收益率的时序图

图2上证50股票指数复合收益率时序图

由图2可知：复合收益率序列大体上是平稳的。在2015年2月份以前，序列波动的幅度较小；在其后的时间段内存在两次较大幅度的变动，分别是2015年6月和2015年8月，股指收益率存在由高转低的下降情况。

3.2.2收益率序列的平稳性检验

本文选用ADF检验法对上证50复合收益率时间序列进行平稳性检验，检验结果如下：

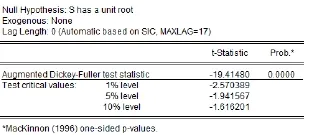
图3上证50收益率序列平稳性检验

检验结果显示，单位根检验的Mackinnon检验临界值小于ADF临界值，因此拒绝有一个单位根的假设，说明复合收益率序列是平稳的。

3.3回归移动平均模型的建立与Chow检验

3.3.1ARMA（p，q）模型的建立

由ADF检验可知，上证50复合收益率序列是平稳的，可以采用Box—Jenkins模型对其进行处理。观察其自相关和偏相关函数图像，发现滞后4阶的函数值超出下限，选用ARMA（p，q）模型对其进行描述。

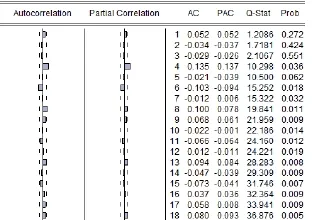
图4上证50股指复合收益率序列｛Pt｝的相关图

对比不同p，q取值下的检验统计量，发现p=q=4时，方程拟合效果最佳。ARMA（4，4） 自回归移动平均方程及其统计量：

St=-0.764620St-4+0.887881ut-4

Se=（0.056232） （0.078757）

t=（15.78948） （-9.708658）

根据（I）式所得结果，我们发现各参数的 t统计量的绝对值均大于 2，因此拒绝参数为 0的原假设，认为ARMA（4，4）模型是有效的。

3.3.2ARMA（4，4）模型的Chow转折点检验

上证50股指期货的推出可视为一项重大的政策和制度，在实证分析中这种影响主要表现为模型参数的改变。Chow转择点检验就是依据对事件发生时间的了解，进而将样本分段，检验模型前后参数有无显著变化。对于ARMA（4，4）模型的Chow转折点检验如下所示：

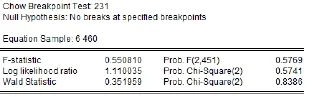
图5ARMA模型Chow转折点检验

输出结果显示，F统计量的p值为0.5769大于0.05，表明事件日前后序列均值方程结构并未发生显著变化。3.3.3 ARMA（4，4）模型是否存在ARCH效应的检验

对上证50复合股指收益率模型是否存在条件方差进行ARCH检验［8］，结果如图6所示。

图6ARCH-LM检验输出图

ARCH检验统计量的p值为0.0003，小于0.05。表明在5%的显著性水平下，上证50股指复合收益率的ARMA（4，4）模型残差存在ARCH效应。

3.4波动率方程的建立

由前文分析可知，2015年4月16日前后上证50股指收益率序列均不服从正态分布，且收益率模型的残差存在ARCH效应。对于这一问题，本文使用GARCH 族模型对其进行分析。GARCH系列模型考虑了时间序列可能存在的异方差问题，并将条件方差视为滞后条件方差及误差平方项之和，是金融时间序列分析中一种常用的分析方法［9］。

一个 GRACH（1，1）过程的样本方差可以写成如下形式：

当1β的值等于 1时，GARCH（1，1）模型转化为ARCH（1）模型，条件方差方程中不存在滞后预测方差。

Zakoian（1990）和Glosten、Jagannathan、Runkle（1993）分别独立提出了 TARCH模型，其条件方差形式相比于GRACH模型增加了一个虚拟变量，用来刻画不同消息对条件方差的影响：

ε ＜

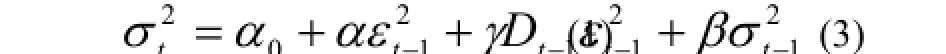
当t0时，D=1；反之，D=0。若的系数γ等于0表示波动不对称现象不显著；否则，认为波动不对称现象存在。

EGARCH模型，又称指数GRACH模型，条件方差被指定为：

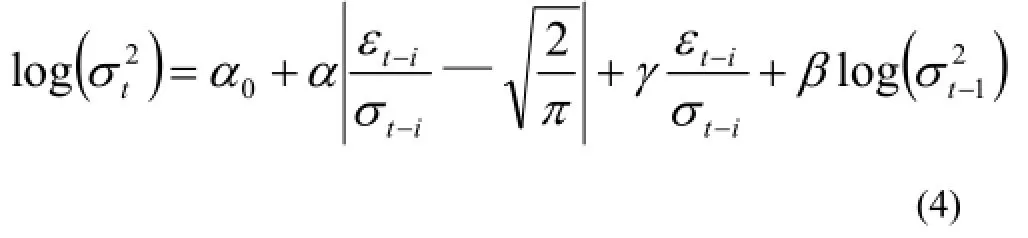
等式左边是条件方差的对数，这意味着杠杆影响是指数的。如果 0≠γ ，则冲击的影响存在着非对称性。采用上述三种模型对事件日前后上证50股指收益 率的ARMA（4，4）模型进行条件方差分析，分析结果如下：

表1股指期货推出前上证50股指收益波动的GARCH回归结果

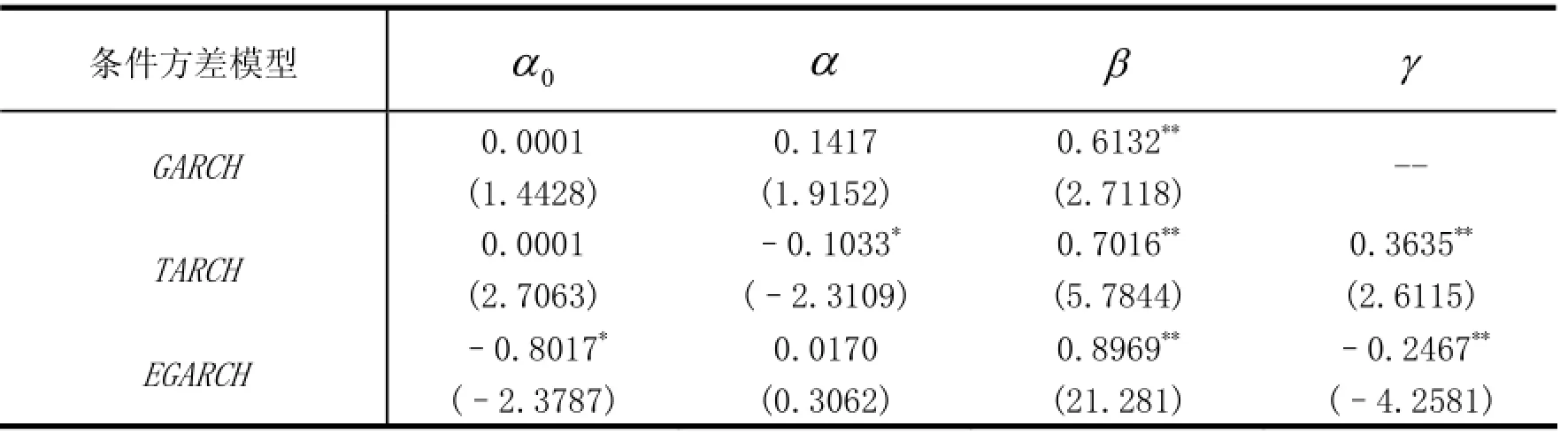
表2股指期货推出后上证50股指收益波动的GARCH回归结果

在所建立的GARCH系列模型中，系数α可以反映T-1时刻股指波动对T时刻股指波动的影响；而β反映的则是股指收益率St自身波动性的提高或降低。

由于GRACH和EGARCH模型中α系数不显著，TARCH模型中的α系数由0.0792变为-0.1033，说明事件日后，T-1时刻股指波动对T时刻股指波动的影响逐渐增大。股指期货上市后，GRACH族模型的β系数均随之降低，说明股指收益率St自身波动性的降低。表5 中TARCH模型γ系数大于0和EGARCH模型γ系数小于0，说明股指期货上市后上证50股指收益率存在了非对称效应，即等量的利空信息比利好信息对现货市场造成了更大的波动。

4结论与建议

实证分析的结果表明：股指期货上市后上证50指数平均收益率存在一定的下降，且标准差较之前有一定幅度的上升。但均值和标准差容易受到极端数据的影响，如2015年6月份就出现了由于场外配资而引发的股市异常波动现象，因此需要进一步对其进行分析。本文所构建的上证50股指复合收益率的ARMA （4，4）模型的Chow检验显示：事件日前后序列均值方程结构并未发生显著变化。针对ARMA （4，4）模型残差所存在ARCH效应，本文选用GARCH族模型对条件方差进行拟合。发现事件日后，描述股指收益率St自身波动性的Beta系数均发生下降，说明股指期货的上市对现货市场的稳定起到了一定的促进作用，但同时也造成了股指收益率非对称效应。

由此可以看出到我国股票市场的运行是平稳的，股指期货的上市对现货市场并未造成过大的冲击。更多种类股指期货的推出标志着金融衍生工具在我国的快速发展，表明我国金融市场改革的不断深化。同时，积极有序和体制健全的资本市场也能够促进实体经济的运行。另外，股指收益率非对称效应的形成表明相关职能部门还应加强对上市公司信息披露机制的监管，以切实保护投资者权益和维护市场稳定。

［1］何东桓.沪深 300股指期货对股票现货市场的影响研究［D］.西南财经大学，2012.

［2］杨艳军，张琳.股指期货对现货波动性和信息传递速度的影响——基于沪深 300数据的实证［J］.中国证券期货，2010（09）：17-18.

［3］曹森，张玉龙.沪深300股指期货对现货市场影响的实证研究［J］.统计与决策，2012（10）：153-156.

［4］熊熊，韩笑.应用时间序列分析的股指期货上市前后沪深300指数特性的变化［J］.重庆理工大学学报：自然科学版，2014（10）：110-115.

［5］刘振毅.沪深 300股指期货上市后对中国股市影响分析［J］.经济视角：下，2011（07）：60-62.

［6］郦金梁，雷曜，李树憬.市场深度、流动性和波动率——沪深300股票指数期货启动对现货市场的影响［J］.金融研究，2012（06）：130-134.

［7］Engle R F.Autoregressive Contidional Heterosceda -sticity with Estimates of the Variance of United Kingdom Inflation［J］.Econometrica， 1982，50：987-1008.

［8］何兴强，孙群燕.中国股票市场的杠杆效应和风险收益权衡［J］.南方经济，2003（09）：62-65.

［9］刘毅.我国股票市场波动非对称特性的研究［D］.上海：同济大学，2008.

F064.1；F713.35

A

1004-4310（2016）04-0114-04

2016-04-26

徐棣（1975- ），男，硕士研究生，会计师，研究方向：金融。