基于电路化简教学结点电压法

赵　强　郭超修

(华东师范大学物理系，上海　200241)



基于电路化简教学结点电压法

赵强郭超修

(华东师范大学物理系，上海200241)

针对结点电压法的教学，依据现代教育理论，通过将复杂电路的无源支路视为含有电动势为零的恒压源的有源电路，并对每个支路用电流源模型等效变换，然后进行简单化简的方法，对结点电压法进行了推导分析.相较于教材中通用的论述，使用的均为学生熟悉的简单方法，快捷地获得了更具有普遍性的表达式，并且能够直观明确地对物理含义进行诠释，以及轻松地实现拓展.在认知过程中，增强了稳固知识的形成，从而实现了对教学效果的提高.

结点电压法；电路化简；诺顿定理

支路电流法和结点电压法是求解复杂电路的基本方法.在教学中，通常将结点电压法安排在支路电流法之后，并使用支路电流法来推导出结点电压法的结论[1-3].然而，对于不同的教学情境，从电路分析的效率以及教学效果来看，采用这种方法并不是最佳途径.

根据现代教学理论，在教学过程中，将新的知识与已有的知识，特别是稳固知识(robust knowledge)之间建立关联，并且使编码过程富有意义和效果，这不但有利于有效地激活先验图式，也有利于实现相关记忆的激活扩散，以及融合构建，从而可以实现教学效果的改善[4-7].本文将从提高教学效果的角度，使用简单的电源模型变换和串并联电路化简的方法对结点电压法的教学给予探讨.

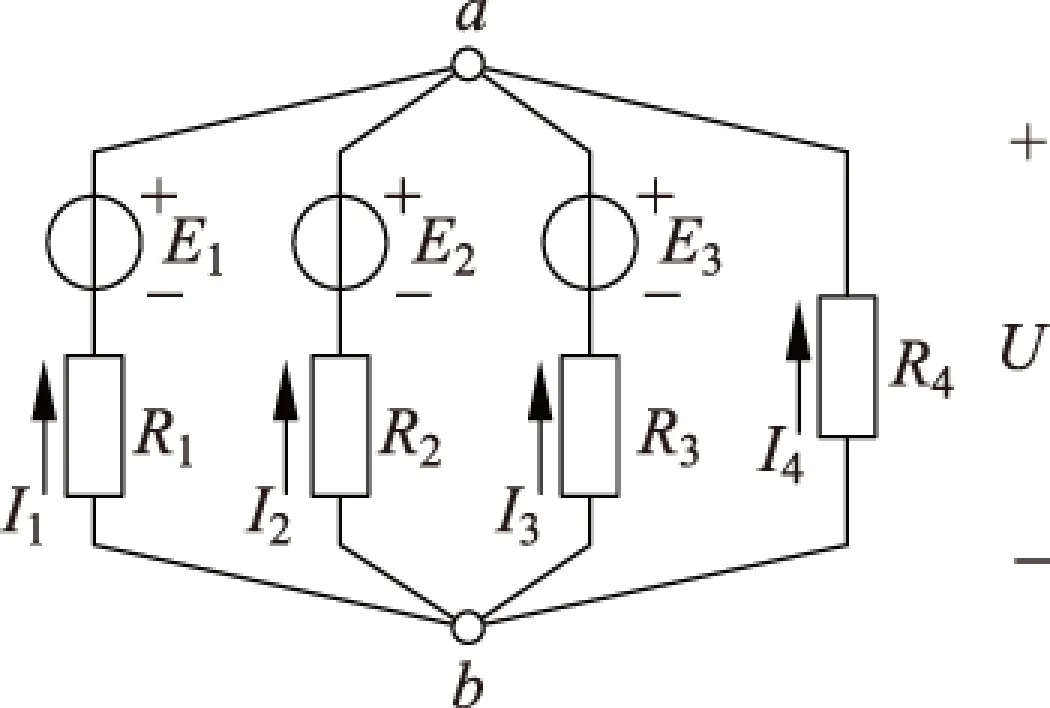
图1　教学结点电压法的电路图

讲解结点电压法时，通常使用类似于图1所示的电路.由于支路I4中没有恒压源，所以看上去电路比较复杂，而且使得使用支路电流法得出教材中常见的式(3)所示结论时，无法直观地获得简洁且意义明确的物理诠释.但是，若将电路中的I4支路看作是一个电动势为零的理想电压源E4和电阻R4串联，那么，电路的每个支路都可以看作是由一个电压源构成(如图2所示).同时，因为需要计算的a、b两个结点间的电压可以被看作是电路对外的输出特性(譬如当a、b两结点间连有一个阻值为无穷大的负载电阻的情形)，所以可以将每个支路的电压源等效变换为电流源，得到图3所示的等效电路.各等效的理想电流源的电流分别为

(1)

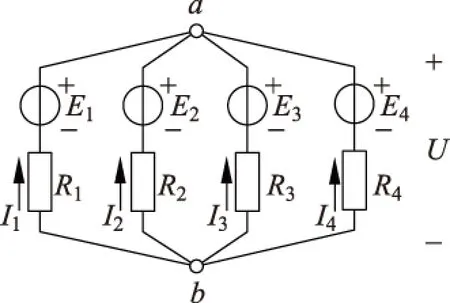
图2　等效电路

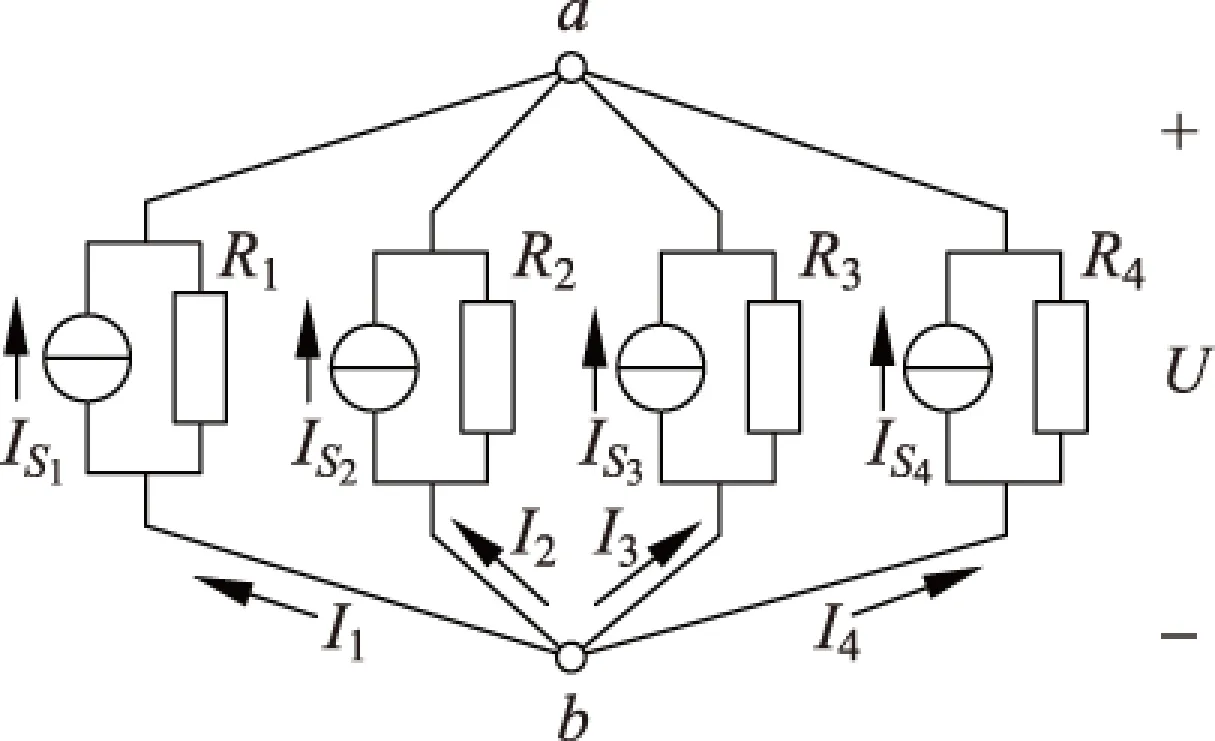
图3　等效电路(采用电流源模型)

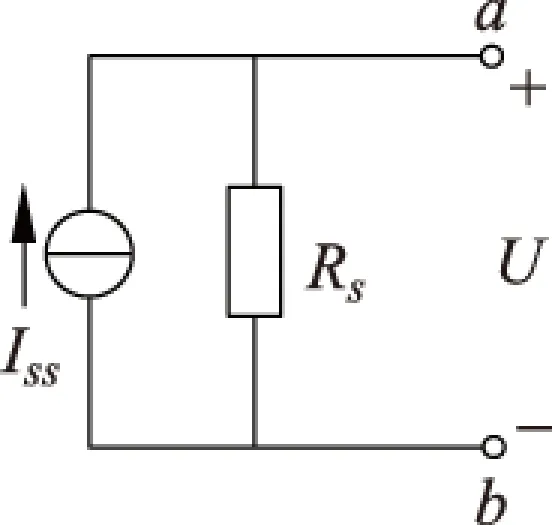
图4　合并后的等效电路

更进一步，此电路又可以等价为一个IS S=IS 1+IS 2+IS 3+IS 4的理想电流源和一个阻值为RS=R1//R2//R3//R4的电阻组成的电流源( 见图4).故而

(2)

由于E4=0，得出教材中常见的使用支路电流法得到的结果

(3)

因此，采用上述方法只需要电源模型的等效变换和串并联化简这两项基本的电路分析方法，对结果中的每一项的物理含义可以给予明确的诠释.同时，省去了使用支路电流法分析时繁琐的基于KVL和KCL来构建方程组并求解的过程.

特别是当某支路n可以等效为仅有一个理想电流源(无伴电流源)IS n的情形，可以直接由式(2)得出式(4)的结论.而对于仅仅从支路电流法推导出式(3)的情形，同学们就很难简洁迅速地得出式(4)这样的对式(3)的扩展.

(4)

因此，可以看出，基于电路化简的方法，将式(2)作为结论，比式(3)作为结论要更直观、更具有通用性，更容易与已经掌握的基本概念建立有力的关联.另外，同学们即使没有记住式(3)所示的结点电压法的结论，也能够快速推导出式(2)或式(4).

进一步可以得出，若将图1所示的电路看作是结点a和b作为两个端点的有源线性二端网络，就可以等效为一个如图4所示的电流源，并且电源的IS S等于a、b两个端点短路时的电流，RS是将所有电源置零后的无源二端网络的电阻.也就是，当电路为图1情形时证明了诺顿定理.当然，只要稍作拓展就可以完全证明稳恒电路的诺顿定理.

由上可知，使用本文所述的方法进行分析推导，可以快捷地得到结点电压法的更为普遍的表达式，能够直接处理含有无伴电流源支路的情形.相对于使用支路电流法，从对结论的物理含义的理解、记忆以及分析应用思路的拓宽的角度来看，更加有利于提高教学效果.经过在教学中实践验证，已对上述教学效果的分析结论给予了充分的肯定.

[1]秦曾煌，姜三勇.电工学[M].7版.北京：高等教育出版社，2009.

[2]林红，杨凡，杨桦，等. 电工技术[M].北京：清华大学出版社，2003.

[3]李瀚荪.电路分析基础[M].4版.高等教育出版社，2006.

[4]Richey J E, Nokes-Malach T J. Comparing four instructional techniques for prompting robust knowledge[J]. Educational Psychology Review, 2015, 27: 181-218.

[5]Kinjo H, Snodgrass J G. Does the generation effect occur for pictures[J]. American Journal of Psychology, 2000, 113: 95-121.

[6]Radvansky G A. Situation models, propositions, and the fan effect[J]. Psychonomic Bulletin & Review, 2005, 12: 478-483.

[7]Anita Woolfolk. Educational Psychology[M]. 10th Edition, Pearson Education, Inc., 2007.

■

TEACHING THE NODE VOLTAGE METHOD BASED ON THE CIRCUIT SIMPLIFICATION

Zhao QiangGuo Chaoxiu

(Department of Physics, East China Normal University, Shanghai 200241)

In order to improve the teaching effect of the node voltage method according to the modern educational principles, each branch of the complicated circuit is considered containing a voltage source, and is equivalently transformed into a current source model in this paper. Namely, the circuit is simplified to be a parallel connection. Consequently, the node voltage method is deduced by basic circuit simplifications, and a more universal expression is obtained. In comparison with the textbooks, we use simpler methods that are familiar to students and quick access to the more universal expressions, which explain the physical meaning clearly and are easy to expand. Our method helps the students enhance the promotion of the robust knowledge in their cognitive process, and finally increases the learning outcome.

node voltage method; circuit simplification; Norton’s theorem

2015-05-04;

2016-01-04

上海市大学生创新项目基金(项目编号201410269037).

赵强，男，副研究员，主要从事物理教学研究工作，研究方向为物理学科教学论.zhaoqiang@phy.ecnu.edu.cn

引文格式: 赵强，郭超修. 基于电路化简教学结点电压法[J]. 物理与工程，2016，26(3)：24-25，28.