跨学科任务驱动教学法在工程项目风险管理教学中的应用

王晓明, 姚宇峰, 吴浙文, 冯　敏

(1. 中国矿业大学 银川学院, 宁夏 银川　750011； 2. 宁夏大学 土木与水利工程学院, 宁夏 银川　750021)



跨学科任务驱动教学法在工程项目风险管理教学中的应用

王晓明1, 姚宇峰2, 吴浙文1, 冯敏1

(1. 中国矿业大学 银川学院, 宁夏 银川750011； 2. 宁夏大学 土木与水利工程学院, 宁夏 银川750021)

层次分析法和模糊数学分析法是工程项目风险分析的常用方法,也是工程项目风险管理课程的教学难点。在学生尚不完全具备足够工程专业知识时,通过采用跨学科任务驱动教学法作业设计,指导学生应用这两种方法,收到了意想不到的教学效果。这不仅是一次工程项目风险管理的课程教育,也是一次有益的就业教育尝试。

跨学科任务驱动教学法； 工程项目风险管理； 层次分析法； 模糊数学分析法； 就业教育

1　层次分析法和模糊数学分析法跨学科教学

在工程项目风险管理课程[1]的教学中,层次分析法和模糊数学分析法是常用的两种分析方法,而掌握这两种方法既是教学重点,也是难点。难处主要表现在:一是需要应用线性代数和模糊数学方面的知识，一部分学生高等数学基础不牢固,应用这一部分内容有一定困难。二是学生必须做这方面的作业训练,以牢固掌握这两种方法,由于工程项目风险管理课程开设较早,学生的工程专业知识储备较少,也没有相应的工程实践知识,要完成工程项目风险的专业分析作业,显得十分困难。对于第一个问题,可以采用课前预习、课堂适当复习的方法加以解决。对于第二个问题,采用跨学科任务驱动教学法[2-4]作业设计,先避开工程理论和实践知识缺乏的困境,让学生在自己感兴趣而又比较容易应用这两种方法的领域里进行风险数据的采集、归纳、计算、分析。通过这样的实践作业过程实训,熟练掌握这两种分析方法的精髓和要领。

目前,高等教育界关于跨学科教育有多种理解。有人认为跨学科是两门以上学科交叉融合,以有效解决单门学科无法解决的问题，跨学科教育易于形成各种知识的交汇与碰撞,更具创新教育色彩[5]。有人认为跨学科是由不同学科互相渗透、彼此结合而产生的新学科，跨学科教育是培养具有多学科知识背景、知识与能力结构合理、基础扎实、素质全面、适应性强的综合性人才的关键[6]。尽管跨学科教育有多种表述[7-9],但都认为,跨学科教育适应了现代科学技术发展综合化、社会问题复杂化的发展趋势,提高了高等教育的教学质量,对于培养学术理论创新人才和高级复合型应用人才具有特别的重要意义。我们经过近4届学生的课堂教学实践,结合学生对人生道路的热情关注,不断摸索,设计了这次跨学科实践作业。

2　跨学科任务驱动教学法的作业设计

每个大学生毕业后都面临着人生道路的选择问题，如就业、创业、承继家族企业、继续学业(考研、出国深造等)等，不管走那一条道路,都是有风险的,有家庭经济能否承受的风险、有能否找到理想工作的风险、有工作后能否实现自我价值的风险、有社会能否提供就业或创业所需各种资源的风险等。

本实践作业要求学生应用风险分析的方法,分析本人大学毕业后可能遇到的风险,选择适合自己的人生道路,确定毕业后哪一种道路风险最小,如何应对将来可能遇到的风险。

2.1必做部分:应用层次分析法确定本人大学毕业后的人生道路

每人至少要分析出适合自己的3项风险,至少要选出2种适合自己的人生道路。

2.1.1构造阶梯层次结构模型

实线表示作业至少要有3项风险,至少2种毕业后道路。虚线表示可进行更多选择的示例。每一项内容,学生可根据自己的实际情况进行调整,不受限制。图1中各因素的内涵,对每个人都是不同的,如理想工作就有专业对口、工资高、生活工作在大城市、工作轻松、有发展前途等不同的含义,可根据自己的真实想法,如实表述。

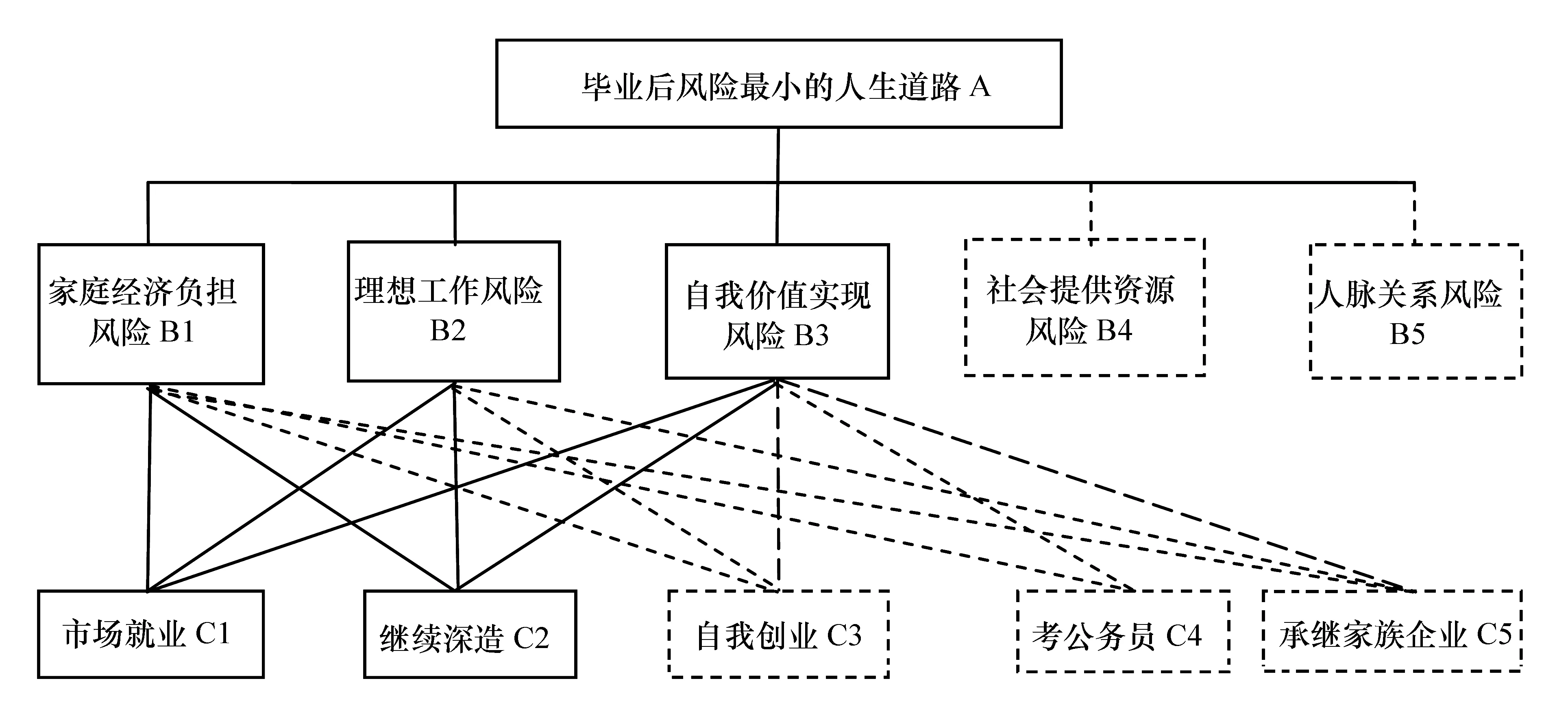
图1　大学毕业后可能遇到的风险阶梯层次结构模型

2.1.2构造比较矩阵

根据两两比较原则,确定各层次不同因素的风险重要性权数。从总目标(A)到风险层(B),将各风险因素两两比较,按判断矩阵中各元素确定的标度表(1—9个标度),得到判断矩阵A中aij的数据。同理,从风险层(B)到方案层(C,即毕业后的道路),针对每个风险因素都有一个判断矩阵,即对比的两方案对所取的若干风险经比较后,得到若干判断矩阵B1、B2、B3…。

2.1.3计算各比较判断矩阵的特征向量

按课堂理论授课中介绍的和积法确定权重,分别计算判断矩阵A和B1、B2、B3…的特征向量,分别用WA和WB1、WB2、WB3表示。主要步骤是:

(1) 求归一化矩阵,得到

(2)将归一化矩阵B的行向量的元素按行相加

(3) 将向量M=(M1, …,Mn) 归一化,得到特征向量W

2.1.4求最大特征值,并进行一致性检验

(AW)i即向量AW的第i个元素。计算一致性指标C.I.和一致性比率C.R.,按随机性指标R.I.数值表,矩阵一致性是否满意,权重是否可以接受。

2.1.5层次加权,计算综合权重,得出决策结论

在计算出各层次要素对上一层次某一要素的相对权重(即重要度)后,即可进行总排序,采用从上而下的方法,逐层求出各层次要素对系统总体的综合重要度,对所有项目的风险因素或预期进行优劣排序,就可得出决策结论。

一般情况下,第二层的单排序结果就是总排序结果。

假定已经算出第k-1层nk-1个元素相对于总目标的权重向量为:

第k层nk个元素对于上一层(第k-1层)第j个元素的权重向量是:

其中不受j支配的元素的权重为零。则得出nk×nk-1阶矩阵

那么,第k层nk个因素对最高层次的相对重要性权重向量为

当决策评价模型有m个层次(不含总目标),把备选方案作为m+1层,各方案对总目标的权重分别为W1,W2,…，Wn,则W=(W1,W2,…，Wn)可按下式计算

W值就是各层次的综合加权权重,结果矩阵中最小数值的元素对应的方案就是风险最小的毕业后人生道路。

2.1.6对结果进行讨论

(1) 应用层次分析法,影响毕业后人生道路选择准确性的因素有哪些？

(2) 如何去应对毕业后可能会遇到的人生风险？

(3) 通过这次实践作业,你有什么收获和建议？

2.2选做部分:用多种风险分析方法综合确定本人大学毕业后的人生道路

本实践作业要求学生通过风险因素排序和整体风险评价,应用风险因素分解法、专家调查法、层次分析法、模糊数学分析法等方法的综合,选择适合自己的几种人生道路,确定毕业后哪一种道路对自己的风险最小,找出影响自己人生道路最大的风险因素,自己将来人生总体风险怎样,如何处置。

2.2.1应用风险因素分析法对各种人生道路的风险进行分类

要求:作出风险因素指标体系树状图(层次图),尽可能将自己毕业后可能的人生道路及每种道路可能的风险都列出来。

准则层(自己的人生道路),至少要列出5种。

指标层(各种人生道路可能遇到的风险),每种人生道路至少要列出2项风险,列出的风险越多越符合实际,风险预测的结果的可靠性就会越高。

2.2.2应用专家调查法进行风险识别

(1) 做出自己的人生道路风险调查表。请每位咨询者(专家)按表1中要求进行两两比较,填写标度值。也可通过电话询问、网上联系各位咨询者确定他们判断的标度值。

表1　风险调查表

(2) 至少要选8名咨询者。 其中要有父母、亲戚、同学、朋友等各方面的人,面越广、人越多,风险预测的

结果的可靠性就会越高。注意:要向每位咨询者解释清楚自己所确定的指标内容的真实确切的含义,每位咨询者一张表。

2.2.3构造判断矩阵,求解特征向量

(1) 根据各位专家给出的标度值,构建判断矩阵。

(2) 应用权重向量计算表确定权重向量。

2.2.4进行一致性检验

(1) 计算最大特征根λman。

(2) 计算判断矩阵一致性指标。

(3) 随机一致性比率计算。

(4) 确定一致性检验结果。

2.2.5各评价指标的最终权重值ω的计算

对每位咨询者都进行上述1.2.3、1.2.4 两项步骤,将各位咨询者的风险因素权重值计入“咨询者对自己人生道路风险因素权重计算汇总表”。求出平均值,作为各评价指标的最终权重值ω。

2.2.6计算指标层总排序值,列出总排序表

指标层某因素的总排序权重向量值=

该因素最终权重值ω×相应准则层最终权重值

2.2.7指标层各因素总排序

根据指标层各因素总排序权重向量值,按从小到大的顺序进行排序,可得出自己人生道路各种风险大小的排序。

2.2.8应用模糊综合评价法进行整体风险评价

(1) 构建评语集。采用五级评语集,建立模糊综合评判模型,即高风险、较高风险、中等风险、较低风险、低风险,与之相应的评语集为:

(2) 咨询者评语调查。设计调查表,选8名以上咨询者进行调查,其中要有父母、亲戚、同学、朋友等各方面的人,面越广、人越多,风险预测结果越接近实际。

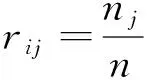
(4) 作出模糊评价模型。模糊评价模型B=ω·R,式中ω在层次分析2.2.5节中已求得。分析结果矩阵中B1,B2,B3,B4,B5各向量,按最大隶属度原则,数值最大者所对应的评语集中的风险程度就是本人未来人生道路的总体风险的程度。

分析结果矩阵中B1,B2,B3,B4,B5各向量,按最大隶属度原则,数值最大者所对应的评语集中的风险程度就是本人未来人生道路的总体风险的程度。

2.2.9对结果进行讨论

(1) 通过风险因素排序,确定出影响自己大学毕业后人生道路的最大风险因素有哪些。

(2) 通过整体风险评价自己大学毕业后人生道路的总体风险状况如何，如果风险较大,应采取什么方法去应对，如果风险较小,自己是否会高枕无忧。

(3) 你认为本次自己人生道路风险分析的结果可靠吗？应用风险因素排序和模糊评价矩阵的方法,影响其评价结果准确性的因素有哪些。

(4) 通过这次实践作业,你有什么收获和建议。

3　采用跨学科任务驱动教学法的教学效果

3.1激发了学生的学习兴趣

(1) 学生作业完成情况好。这次实践作业没有按常规安排的选工程项目的案例作风险分析,而是选择了学生非常关心的毕业后的去向问题作风险分析,引起了学生的很大兴趣和热情。尽管作业有相当大的难度,数据收集、计算、分析、处理很麻烦,需要广泛调查、征求意见,还要认真复习或学习线性代数、模糊数学等课程,但在7周的课余时间里,98%的学生都完成了作业,其中部分学生还完成了选作部分,一份作业多者达到20多页,学生基本上掌握了层次分析法和模糊数学分析法。

(2) 抄袭作业的现象大为减少。每位学生都想知道自己毕业后人生道路的风险,而每个人的人生道路和风险因素是不一样的,计算的过程、结果也是不一样的,因此,几乎不可能出现完全一样的作业。一些经常抄作业的学生这次也能够如期完成作业。

3.2提高了学生的综合能力

(1) 学生的调查研究和社交能力得到了锻炼。采集数据是理工科学生应具备的一项基本技能。本次实践作业如果采用工程案例作风险分析,数据要到工程现场或相关单位去收集,这对学生来讲,条件不具备,显然是做不到的。但让学生用自己的人生道路去做风险分析,其数据可以从自己的家庭、同学、朋友、社会各方面去采集,这使本次实践作业就具备了可行性、可操作性。

(2) 学生计算机网络技术应用能力得到大幅提升。此次作业设计,学生不仅要从书本、课堂上得到知识,还要借助网络平台查阅文献资料,因此利用计算机收集、整理和处理数据的能力得到了锻炼和提高。

(3) 学生的数学应用能力得到提高。线性代数、模糊数学等课程是比较抽象的,很多学生对这些课程的学习感到困难,也不会应用，但在这次实践作业中,将这些抽象的数学知识应用到了自己的实际生活中,对学生数学能力的提高很有帮助。

(4) 学生的就业意识和就业风险意识大大增强。学生越早具有这些意识,越有利于他们将来的就业。通过这次作业,学生用科学的方法了解了自己的不足和未来的风险,有利于他们及早调整自己的就业目标,尽早克服自身的缺点或不足之处。

(5) 学生的价值观、人生观更加成型。这次实践作业,使学生对当前社会对人才的需求和自己的人生道路有了一次比较认真、理性的思考。学生通过这次实践作业，意识到自己的人生是有很多风险的,对学生心灵的触动和人生启迪胜于一般的说教,对他们人生道路的长远发展非常有益。

3.3教学互动更加频繁

此次跨学科任务驱动[10-12]案例教学,教师不仅是指导者,也是管理者、参与者。教学过程中,教师先是主题讲解,让学生明白理论依据、过程方法,然后通过布置任务,看学生是否掌握了理论知识和具体过程操作,通过阶段性成果的收集、整理及评阅,加强过程教学管控,增强教学互动,环环相扣,教学相得益彰。

4　跨学科教育的问题探讨

4.1跨学科教育的认识性问题

工程项目风险管理属工程管理专业的课程,而学生的就业问题是管理专业课程,通过长达7周课余时间的实践作业将二者结合到了一起,就有了跨学科的效果。当然,仅这种方法还远远达不到上述跨学科教育内涵的高度和深度,但这毕竟是在跨学科教育改革道路上初始探索,而要在这方面取得更有效的成就,还需要各级组织、教师、学生及各方面志士仁人多方面的共同努力。

4.2数据调查的可靠性问题

这次实践作业原始数据的来源是否真实、客观、广泛，是否符合实际要求,对最终结果的可靠程度有很大的影响。从学生最终成果来看,认真进行原始数据调研的学生,得出的结论可靠性值得肯定。而学生对调查对象的选择与沟通,以及调查资料的收集、加工、整理,本身属于管理学科的范畴,这就要求各级组织及教师加强对学生人际交流、公关能力方面的指导,这本身也属于跨学科教育的范畴。

References)

[1] 陈伟珂.工程项目风险管理[M].北京:北京人民交通出版社,2008:25-32,56-57.

[2] 晏湧,蓝波.“任务驱动”教学法在电工电子技术课程中的应用[J].实验技术与管理,2012,29(9):163-166.

[3] 郭利霞.任务驱动教学法在高职PLC课程教学中的应用[J].中国职业技术教育,2007(10):36-37.

[4] 曾祥光.任务驱动教学法在翻转课堂实践中的应用研究[J].中国成人教育,2014(7):130-132.

[5] 孙卫华,郭伟.河北省教育技术学专业跨学科人才培养策略[J].河北大学学报:哲学社会科学版,2014(1):28-31.

[6] 张伟.跨学科教育:普林斯顿大学本科人才培养案例研究[J].高等工程教育研究,2014(3):118-125.

[7] 余胜泉,胡翔.STEM教育理念与跨学科整合模式[J].开放教育研究,2015(8):13-22.

[8] 周慧颖,郄海霞.世界一流大学工程教育跨学科课程建设的经验与启示:以麻省理工学院为例[J].黑龙江高教研究,2014(2):50-53.

[9] 蒋胜楠.美国本科生跨学科教育研究及启示[J].黑龙江高教研究,2015(5):58-61.

[10] 陈涛.任务驱动教学法在高校计算机课程中的应用研究[J].中国成人教育,2014(17):161-163.

[11] 邝明,李雪梅,高悦.土木工程制图研究性教学方案设计及实践[J].工程图学学报,2011(5):61-64.

[12] 佟瑞鹏,刘欣,杜志托,等.适用于安全工程专业的风险管理课程内容体系研究[J].安全与环境工程,2014(21):149-154.

Application of interdisciplinary task driven teaching method in teaching of engineering project risk management

Wang Xiaoming1, Yao Yuefeng2, Wu Zhewen1, Feng Min1

(1. Yinchuan College, China University of Mining and Technology, Yinchuan 750011,China;2. School of Civil Engineering and Water Conservancy, Ningxia University, Yinchuan 750021,China)

The analytic hierarchy process and the fuzzy mathematics analysis method are the common methods of risk analysis of engineering projects. They are also the difficulties in the teaching of engineering project risk management.Through the use of cross disciplinary task driven teaching method,the two methods are used to guide students to apply these methods,when the students are not fully equipped with the knowledge of engineering expertise. The teaching method has received an unexpected effect.This is not only an engineering project risk management of the course of education,but also a useful attempt to obtain employment education.

interdisciplinary task driven teaching method; project risk management; analytic hierarchy process; fuzzy mathematics analysis method; employment education

DOI:10.16791/j.cnki.sjg.2016.06.049

2015-11-10修改日期：2016-03-03

宁夏回族自治区工程管理特色专业建设项目(宁教高[2012]348号)

王晓明(1979—),男,宁夏海原,硕士,讲师,主要从事工程测量、工程项目管理教学工作.

E-mail：wxmxingxiang@126.com

G642.0

B

1002-4956(2016)6-0191-05