基于RBF核支持向量回归的模型预测控制仿真

唐贤伦, 刘念慈, 严　冬, 陈功贵

(重庆邮电大学 自动化学院, 重庆　400065)



基于RBF核支持向量回归的模型预测控制仿真

唐贤伦, 刘念慈, 严冬, 陈功贵

(重庆邮电大学 自动化学院, 重庆400065)

RBF核函数的表达式较复杂,用于模型预测控制时滚动优化求解困难。该文建立一种基于RBF核SVR的预测控制模型,利用多智能体粒子群(MAPSO)算法求解模型预测控制中的滚动优化,推导出最优控制律,对其进行Matlab仿真并与其他方法进行比较。选取一个非线性系统及连续搅拌槽式反应器进行测试分析,结果表明:该预测模型能迅速抑制干扰,较快返回预设跟踪轨迹,展现了良好的抗噪、抗干扰能力。

模型预测控制； 支持向量回归； 仿真实验； 控制系统； RBF

模型预测控制[1-2]是基于预测模型、滚动优化和反馈校正的优化控制算法,其本质是根据对系统未来状态的预测来优化系统行为[3]。支持向量回归机(SVR)[4-6]是一种建立在统计学习理论上的“小样本”学习机,可以很好地解决非线性、高维数、小样本问题。SVR的预测和泛化能力很大程度上取决于其核函数的选取,而传统的SVR凭经验选取核函数使其在具体应用中存在一定风险。RBF核函数是目前应用广泛、预测精度相对较高的SVR核函数,但是由于其本身表达式复杂,在用于模型预测控制时滚动优化求解困难。采用表达式简单的二次核SVR进行预测控制,虽然有较好的效果,但不能避免初期振荡等问题[7]。

为了改进预测控制系统的性能、提高学生的分析能力和理解能力,我们在控制类研究生课程的模型预测控制系统部分的教学中,采用基于RBF核SVR的模型预测控制算法,选取适应性强的RBF核函数作为SVR核函数,将SVR与模型预测控制相结合,对非线性系统进行预测控制。考虑到RBF核自身复杂的表达式,在滚动优化过程中需要数学推导,要求学生将相关算式经泰勒展开后,利用MAPSO算法求出最优控制输出。最后,将该算法与基于二次核支持向量回归的模型预测控制方法进行Matlab仿真并进行比较。

1　多智能体粒子群优化(MAPSO)算法

粒子群算法(PSO)视每个个体为一个粒子,通过迭代寻找最优值。每一次迭代中,粒子通过跟踪个体极值和全局极值更新自己。每个粒子根据如下公式来更新自身速度和位置:

(1)

式中,下标k为当前迭代次数,Xk和Vk分别表示第k次迭代时粒子的空间位置和速度,pk、gk分别代表当前时刻粒子个体最优位置和全局最优位置,c1、c2为加速度因子,r1,r2是分布于[0,1]之间的随机数,w为惯性常数。

在标准粒子群算法基础上,MAPSO算法是结合PSO算法和多智能体(多Agent)的主要特性而构造的一种新算法[8]。在MAPSO算法中,每个粒子(Agent)通过与其邻居粒子的竞争与合作修正自身行动策略,并利用公式(1)与粒子群中最优粒子(最优Agent)进行信息交换,这样能够弥补单个Agent有用信息传递的环境局限性和信息流传递效率低的不足,加快信息在多Agent系统中的流动,提高算法的收敛速度。

2　基于MAPSO的RBF-SVR预测控制

2.1支持向量回归机(SVR)

支持向量机(SVM)可以分为支持向量分类机(SVC)和支持向量回归机(SVR)两种,前者主要应用于辨识分类,后者主要应用于函数逼近。

支持向量回归机的估计函数一般写为

(2)

其中Φ(x)是向量x在高维特征空间的非线性映射,w⊂Rn,b⊂Rn为函数系数。根据结构风险最小化一致性原则,可以确定w和b,向量x可由下式确定:

(3)

式(3)中,Rref(·)是结构风险,Γ(·)为损失函数,C为惩罚系数(C≥0),l为样本数。向量w可以写为

(4)

根据式(4),可将式(2)转化为

(5)

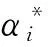
从上述式子中不难看出,SVR核函数的选取直接影响其预测精度和泛化能力。

SVR常用的核函数有sigmoid核函数、多项式核函数及径向基(RBF)核函数。其中RBF核函数应用广泛、适用性强、具有较宽收敛域,几乎任何情况(维数过高过低、样本数据过多过少等)下,均能表现出较理想的效果,因此为本文所选用。考虑其复杂表达式在滚动优化部分不易化简求取最优控制律,在滚动优化部分,先将RBF核函数利用泰勒公式展开成多项式后,再引入多Agent粒子群算法求解滚动优化，进而得到控制律。

2.2非线性预测模型

通常离散被控对象的输入输出关系可以描述为[8]

(6)

式中f是非线性函数,n和m分别为输出信号和控制信号对控制系统输出的最大影响时域长度。

利用SVR对上述被控对象建模,模型的表达式为

(7)

(8)

式中,ym(k+1)表示k+1步模型预测输出,nsv为支持向量总数,Ii为第i个支持向量,ai是Ii相对应的权重系数,b为偏移量,均可通过支持向量回归算法获得。γ是核参数,由MAPSO算法优化确定。式中含未知变量的I(k)可表示为

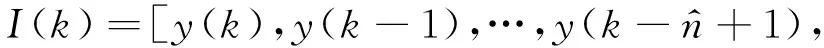
(9)

故

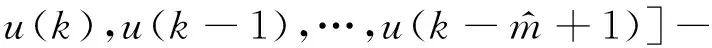
(10)

即

(11)

从式(8)不难看出:含有唯一未知量u(k)的I(k)处在一个尴尬难求解的位置,因此利用泰勒公式将式(8)在零点展开以便求解,式(8)展开后得

其中,x=‖I(k)-Ii‖2。

结合式(11)、(12)不难看出,经过泰勒公式展开后的式(8)中唯一的未知变量u(k)可以轻松地被分离出来,即‖I(k)-Ii‖2可以表示为

(13)

其中,

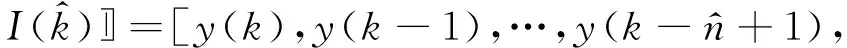
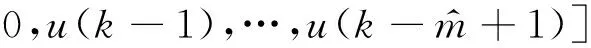
(14)

把式(13)代入式(12)中可得:

(15)

其中,

为了消除模型的失配和系统的随机干扰等不确定因素对控制系统的影响,借助以前的经验值对模型预测值进行校

(16)

式中,y(k)为k时刻被控对象实际输出值,ym(k+1)为k+1时刻的模型预测输出值,yp(k+1)为k+1时刻的校正预测输出值,h为误差权重系数。

2.3滚动优化

滚动优化的目标函数为

(17)

其中,q代表误差权重系数,p代表控制权重系数。yr(k+1)为k+1时刻的参考输出值,一般表示为

(18)

其中,ar为柔化系数(取值范围设定为(0,1)),ysp为真实的设定值。

将式(15)、(16)代入式(17)中得到:

(19)

从式(19)的形式可以看出,这是一个变量有界多项式极值问题,可以通过MAPSO优化算法求取其最小值。具体算法步骤如下:

(1) 种群初始化,初始化粒子和速度,设置相关参数；

(2) 根据适应度函数计算适应值；

(3) 根据邻居信息,更新粒子的个体最优位置；

(4) 根据公式(1)更新粒子的位置和速度；

(5) 判断是否满足终止条件,满足则运算终止,否则转至步骤(3)。

根据以上分析可得基于RBF核支持向量回归的非线性系统模型预测控制的结构框图见图1。

图1　基于RBF-SVR的预测控制结构框图

3　实例分析

为了验证基于RBF核支持向量回归的模型预测控制算法在非线性系统中的预测控制性能,选取一个非线性系统及连续搅拌槽式反应器(complete stirredtank reactor , CSTR)要求学生进行测试分析。实验中,SVR的参数根据经验设定为:C=50,ε=10-4,γ=2.5.

3.1仿真实例1

考虑非线性系统为

(20)

其中,y是被控对象输出,u为控制信号输入。

选取该模型随机生成的100个数据,归一化后分别作为训练集和测试集；跟踪信号分别选取幅值为1的方波和正弦波(见图2)。将基于RBF核的SVR和基于二次核(QP)的SVR两种方法分别代入非线性系统中,模型预测控制效果如图2所示,其跟踪误差(绝对值)如图3所示。

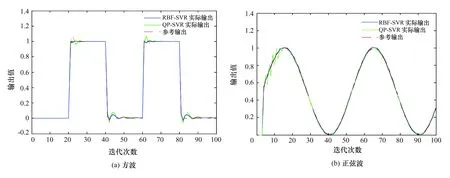
图2　不同核函数的跟踪性能

图3　不同核函数模型的跟踪误差

图2说明基于RBF核的SVR方法在跟踪方波时除了在低位有较明显小幅度超调现象外,都能够很好地跟踪波形,在跟踪正弦波时更是几乎零误差；而基于二次核(QP)的SVR方法则在跟踪方波时高位、低位都出现了较RBF-SVR明显的误差,在超调性、稳定性上都有明显的劣势。图3清晰地显示了基于RBF核的SVR相较于基于二次核的SVR在整体跟踪误差上的明显优势。

3.2仿真实例2

连续搅拌槽式反应器[10](CSTR)是广泛应用于过程工业的非线性化学反应器,可以将其简化为一个非线性系统模型。

一个不可逆的化学反应在CSTR中发生,具体的反应过程可由下式表示:

(21)

若只考虑反应物的浓度,那么有:

(22)

通过CSTR数学模型随机产生100对数据作为SVR模型预测控制算法的训练数据。同理,将两种方法分别代入CSTR模型中,两种算法的模型预测控制效果如4所示,相应的跟踪误差如表1所示。

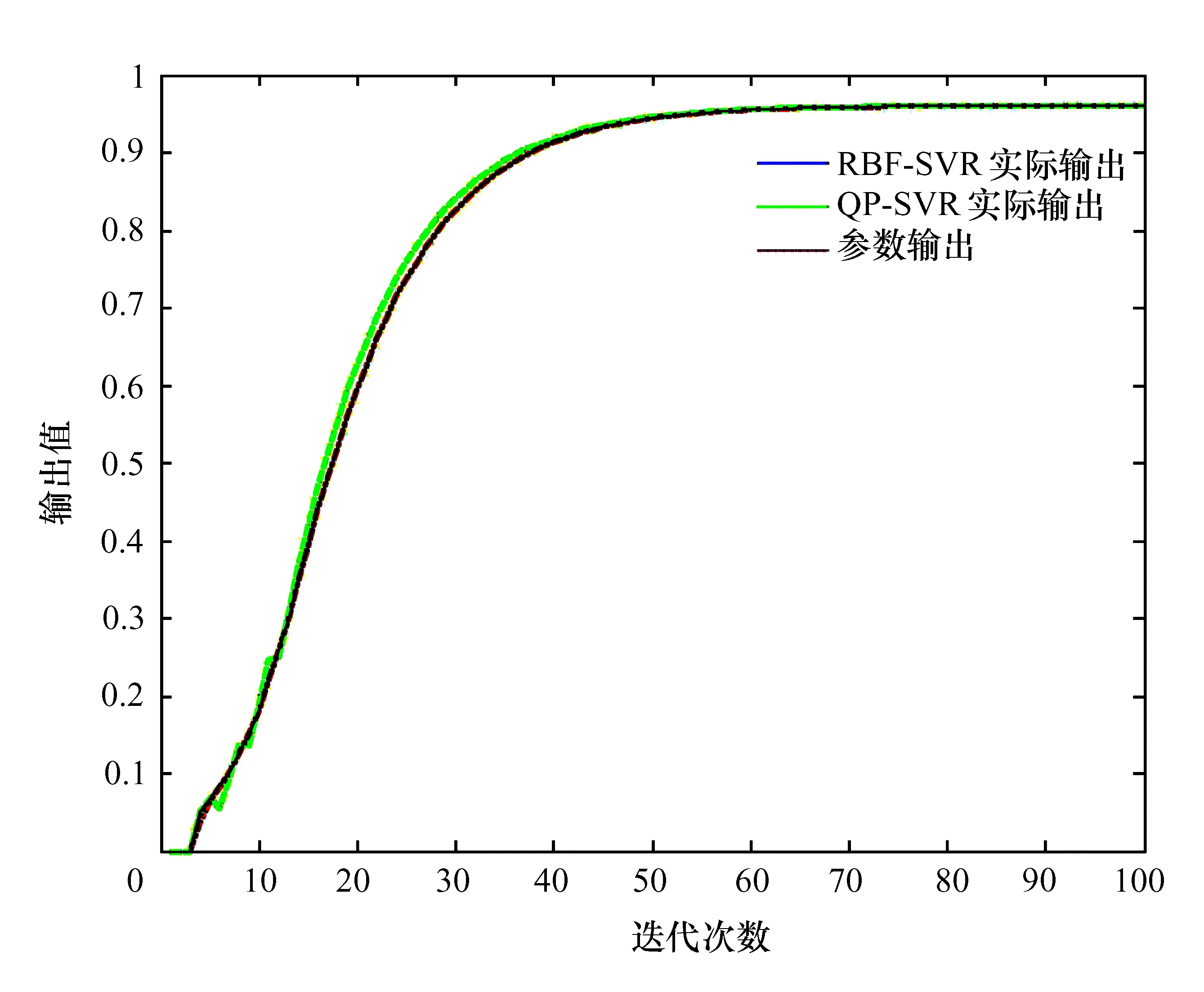
图4　CSTR跟踪性能

算法最大误差最小误差平均误差RBF-SVR10-32*10-43*10-4QP-SVR0.030.010.02

结合图4及表1可以明显看出基于二次核(QP)的SVR算法在最初响应阶段出现了较明显的振荡现象,而且在后续跟踪响应过程中也出现了明显的超调现象。相较而言,基于RBF核的SVR算法除了最初时的微小误差,其余时刻均能很好地跟踪模型参考输出,误差几乎为零。

为了验证两种方法的抗干扰性能,在基于RBF核SVR的模型预测中，k=20时刻加入干扰信号,其跟踪效果如图5所示。

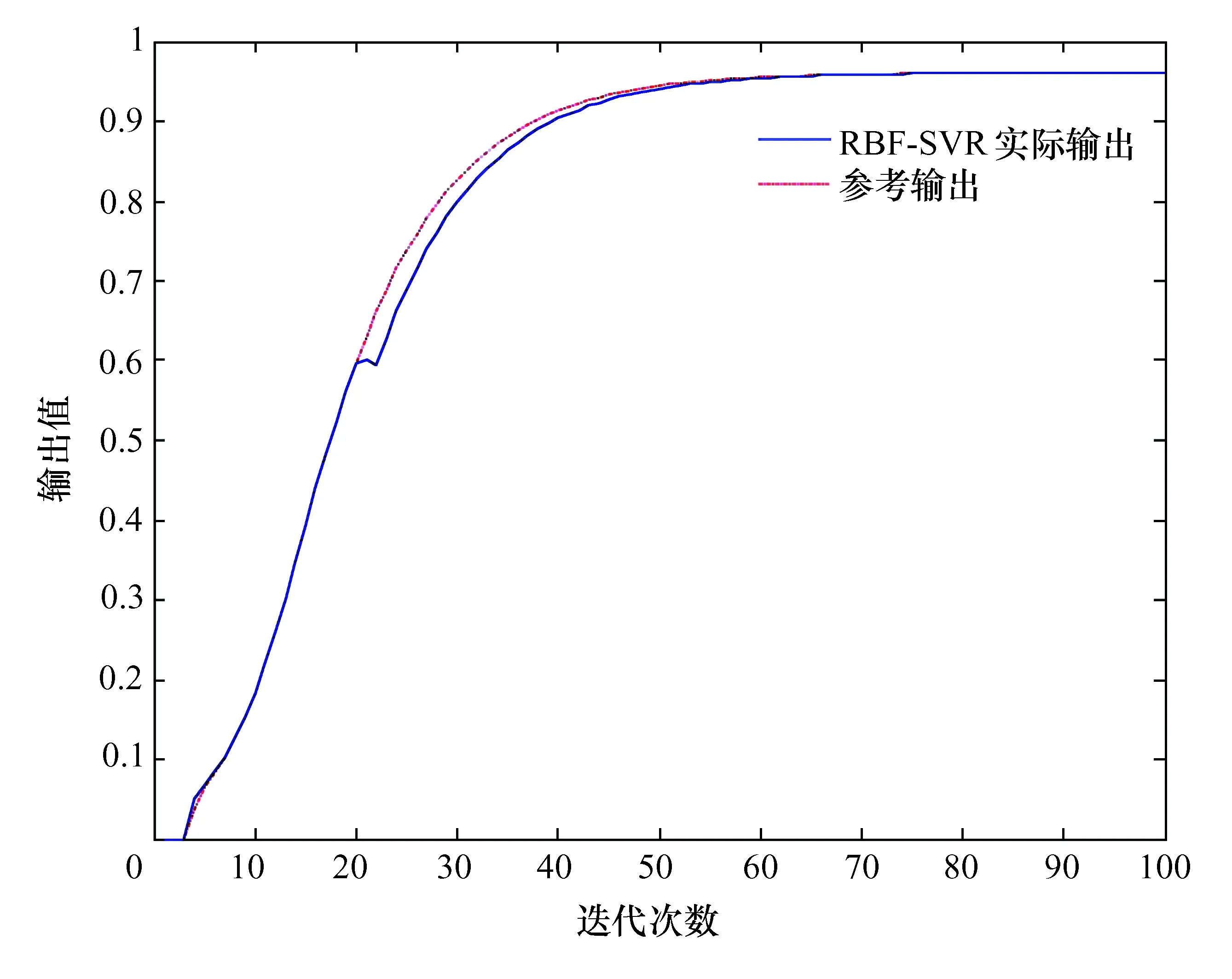
图5　CSTR抗噪性能

从图5能明显看出,基于RBF核的SVR算法在k=20时刻受到干扰后能迅速抑制干扰,较快地返回到预设跟踪轨迹,从而展现了该方法良好的抗噪、抗干扰能力。

4　结语

基于RBF核支持向量回归的模型预测控制算法,能有效解决非线性系统模型预测控制无法得到精确模型、滚动优化求解困难等问题,对非线性系统具有很好的控制性能。通过Matlab仿真实验,学生对基于RBF-SVR的模型预测控制系统有了更深的理解,并根据与基于二次核支持向量回归的模型预测控制算法比较，加强了对预测控制系统的认识。将Matlab仿真技术引入课程教学,提高了学生的实践能力、教学效率和教学质量[11-12]，且仿真实验中丰富和直观的图形及数据,使学生对系统的动态过程有更进一步认识。

References)

[1] 席裕庚,李德伟,林姝.模型预测控制:现状与挑战[J].自动化学报,2013,39(3):222-236.

[2] Ding B. Dynamic output feedback predictive control for nonlinear systems represented by a takagi-sugeno model[J].Fuzzy systems IEEE transactions on,2011,19(5):831-843.

[3] 舒迪前.预测控制系统及其应用[M].北京:机械工业出版社,1996.

[4] Vapnik V N.The Nature of Statistical Learning Theory[M].New York:Springer-Verlag,1995.

[5] Cui Guimei, Sun Tong,Zhang Yong.Application of Suport Vector Machine (SVM) in Prediction of Molten Iron Temperature in Blast Furnace[J].Control Engineering of China,2013,20(5):809-817.

[6] Lai Jinhui,Liang Song.Application of GCS-SVM model in network traffic prediction[J].Computer Engineering & Applications,2013,49(21):75-78.

[7] 包哲静,皮道映,孙优贤.基于并行支持向量机的多变量非线性模型预测控制[J].控制与决策,2007,22(8):922-926.

[8] 唐贤伦,张衡,周家林,等.多Agent结构的混沌PSO在无功优化中的应用[J].电机与控制学报,2013,17(6):15-21.

[9] 穆朝絮,张瑞民,孙长银.基于粒子群优化的非线性系统最小二乘支持向量机预测控制算法[J].控制理论与应用,2010,27(2):164-168.

[10] Zhang Jianzhong, Wang Qingchao. Hammerstein Model Identification of Continuous Stirred Tank Reactor Based on Least Squares Support Vector Machines[C]//2009年中国控制与决策会议(2009 Chinese Control & Decision Conference)论文集.2009:2858-2862.

[11] 刘金颂,张庆阳,苏晓峰,等.Matlab软件在自动控制原理实验中的应用[J].实验技术与管理,2014,31(6):138-140,145.

[12] 李建海,皮之军,张晨亮,等.Matlab/Simulink仿真技术在电机实验教学中的应用[J].实验技术与管理,2011,28(8):79-82.

Study on simulation of model predictive control based on RBF-SVR

Tang Xianlun, Liu Nianci,Yan Dong, Chen Gonggui

(College of Automation,Chongqing University of Posts and Telecommunications,Chongqing 400065,China)

Although the RBF is the most widely used SVR kernel function, the expression complexity of RBF makes it difficult to get analytical formula of rolling optimization in model predictive control. A model of predictive control based on RBF-SVR is established, the multi-agent particle swarm optimization (MAPSO) algorithm is used to obtain the optimal control inputs. For nonlinear systems, Simulation results show that the proposed algorithm has demonstrated excellent adaptive ability and robustness and can be effectively applied to the nonlinear system.

model predictive control; support vector regression; simulation experiment; control system; RBF

DOI:10.16791/j.cnki.sjg.2016.06.027

2015-12-01

重庆市研究生教育教学改革研究项目(yjg143061)；重庆邮电大学校级教改项目(XJG1523)

唐贤伦(1977—),男,四川安岳,博士,教授,主要从事智能控制、系统工程方面的教学和科研工作.

E-mail：tangxl@cqupt.edu.cn

TP273; G434

A

1002-4956(2016)6-0103-05

虚拟仿真技术探索与实践