基于改进引力搜索算法的无功优化仿真研究

陈功贵， 刘利兰， 郭艳艳， 郭　飞

(1. 重庆邮电大学 自动化学院， 重庆　400065；2. 武汉铁路职业技术学院， 机车车辆工程系， 湖北 武汉　430205)



基于改进引力搜索算法的无功优化仿真研究

陈功贵1， 刘利兰1， 郭艳艳2， 郭飞1

(1. 重庆邮电大学 自动化学院， 重庆400065；2. 武汉铁路职业技术学院， 机车车辆工程系， 湖北 武汉430205)

针对引力搜索算法(GSA)在求解电力系统无功优化时出现早熟收敛和局部搜索能力差的问题，引入粒子群算法的记忆功能和加速机制，形成改进引力搜索算法(IGSA)。将GSA和IGSA基于Matlab对IEEE30节点测试系统进行电力系统无功优化仿真。仿真结果表明：IGSA算法避免了早熟现象，增强了局部搜索能力，能获得质量更高的最优解。该仿真实验可加深学生对电力系统无功优化的理解和对智能算法的认识。

无功优化； 引力搜索算法；Matlab； 电力系统仿真

在电力系统运行中，无功功率的分布情况直接影响电力系统的安全性、稳定性和经济性，因此，无功优化是控制电力系统运行的一种重要方式。由于电网结构复杂，无功优化问题成为一个典型的非线性、多变量、多约束、计算量大且同时具有连续型和离散型变量的优化问题[1]。

引力搜索算法(gravitationalsearchalgorithm，GSA)是基于牛顿万有引力定律的一种启发式智能算法，广泛应用于解决复杂优化问题[2-4]。改进引力搜索算法(improvedgravitationalsearchalgorithm，IGSA)则在保留GSA搜索方式的基础上，引入了粒子群算法[5]的记忆功能来更新粒子的速度，并设置了有效的加速因子以平衡引力和记忆对搜索的影响。为验证算法的有效性，利用Matlab软件[6-8]，将GSA和IGSA分别对IEEE30节点测试系统[9]进行30次电力系统无功优化仿真。仿真实验结果表明，IGSA具有更好的收敛特性和搜索能力。

将Matlab仿真融入电力系统无功优化实验教学中，学生可以把相关的理论知识运用到实际仿真中，这不仅加强了学生对无功优化理论的掌握和对智能算法的认识，还增强了学生的实践能力。此外，Matlab仿真中大量直观的实验数据和仿真图形，可使学生更全面地理解系统的优化过程，有效提高教学质量[10-12]。

1　无功优化

无功优化指的是通过调节已知的电压控制设备(包括发电机端电压、变压器抽头变比和电容器的无功补偿)来提高电网经济性的优化运算，其数学模型包括目标函数和约束条件[1]。

1.1数学模型

本文对无功优化研究的目标是使系统有功功率损耗最小：

minf=min{Ploss}=

(1)

式中Np为所有支路集合，Gk为支路k的电导，i、j表示节点数。

根据无功优化问题中的变量和潮流计算的要求，其约束条件为：

有功功率Pi、无功功率Qi为：

(2)

节点电压幅值为

(3)

变压器抽头变比Ti为

(4)

发电机的无功功率为

(5)

电容器无功补偿容量为

(6)

式中，N、NPQ、NT、NG和NC分别表示所有节点数(平衡节点除外)、负荷节点数、投放变压器的支路数、含发电机的支路数和含电容器的支路数；其中节点电压幅值Vi包括发电机端电压VGi和负荷节点电压VLi。

1.2结合罚系数的数学模型

在式(2)—式(6)中，发电机端电压VG、变压器抽头变比T和电容器无功补偿容量QC属于控制变量，在进行无功优化之前就可给定在允许范围内；而负荷节点的电压VL和发电机节点的无功功率QG属于状态变量，其自身不能满足相应的约束条件。为解决该问题，建立了结合罚系数的数学模型，在约束条件不变的情况下，同样考虑系统有功功率损耗最小的目标函数为：

(7)

(8)

(9)

(10)

2　改进引力搜索算法

2.1GSA

无功优化问题的解在GSA中被看作一组在空间运行的粒子，万有引力作用于各个粒子，使其通过相互吸引朝着质量最大的粒子移动，移动过程遵循运动学规律，而质量最大的粒子占据最优位置，该最优位置即是无功优化问题的最优解[13]。

在GSA中，每个粒子的每次迭代都要更新加速度、速度和位置：

(11)

(12)

(13)

式中，xid(k)、vid(k)和aid(k)分别表示第k代粒子i在d维的位置、速度和加速度。d[1,2,…,D]，D是搜索空间的维度；r是[0,1]之间的一个随机数；Fid(k)是第k代粒子i在d维所受引力的大小；Mi(k)表示第k代粒子i的质量。

(14)

(15)

式中，N0表示粒子的个数；Rij(k)表示粒子i和j之间的欧式距离；是一个很小的常量；G(k)为第k次迭代时的引力常数；G0表示初始的引力常量；是一个大于零的常量。

(16)

(17)

式中，fiti(k)是粒子i在第k代时的适应度值；fbest(k)和fworst(k)分别是在第k代时的最好和最差适应度值。

2.2IGSA的应用

由式(11)和(12)可知，GSA在更新粒子位置时只考虑了当前位置的影响，并未考虑粒子的记忆性。因此，在IGSA中引入了粒子群算法的记忆功能和加速机制以寻得更优解。

粒子群算法通过模拟动物群体的捕食行为进行优化搜索，其速度更新公式为：

(18)

引入粒子群算法的记忆功能和加速机制后，IGSA的速度更新公式为：

(19)

通过对c1、c2的调节可以平衡引力和记忆对粒子速度的影响，这在IGSA中形成了很好的加速机制。

将IGSA应用于无功优化中求解，步骤见图1。

3　基于Matlab的无功优化仿真实验

为验证算法的有效性，本文分别将GSA和IGSA对IEEE30节点测试系统进行了30次独立的无功优化仿真，该测试系统初始有功功率损耗为5.832MW[9]。

图1　IGSA的无功优化求解步骤

在仿真实验中，算法的参数设置对程序的运行结果起着至关重要的作用。例如，粒子个数过多会增加算法的计算复杂度和运行时间，过少又不能保证种群的多样性。本文在多次实验中，通过对算法参数作细微的调整，得到2种算法合理的参数设置(见表1)。

表1　算法参数设置

GSA和IGSA分别进行了30次独立的实验，分析实验数据可得每种算法的优化结果(见表2)。

表2　优化结果比较

由表2可知，两种算法的运行时间相差不大，但IGSA的最优、最差和平均目标值都优于GSA相应的目标值，甚至IGSA的最差目标值都优于GSA的最好目标值，这说明改进后的IGSA优化效果更好，能搜索到质量更高的解。根据IGSA的最优优化结果，IEEE30节点系统的有功功率损耗降低了1.031 467MW。若电价按0.5元/(kW·h)来计算，基于IGSA的无功优化24h可节省约12 377元。此外，IGSA较小的标准偏差说明其优化结果的一致性更好。

根据30次的运行结果，GSA和IGSA的平均收敛曲线如图2所示，最优结果分布如图3所示。

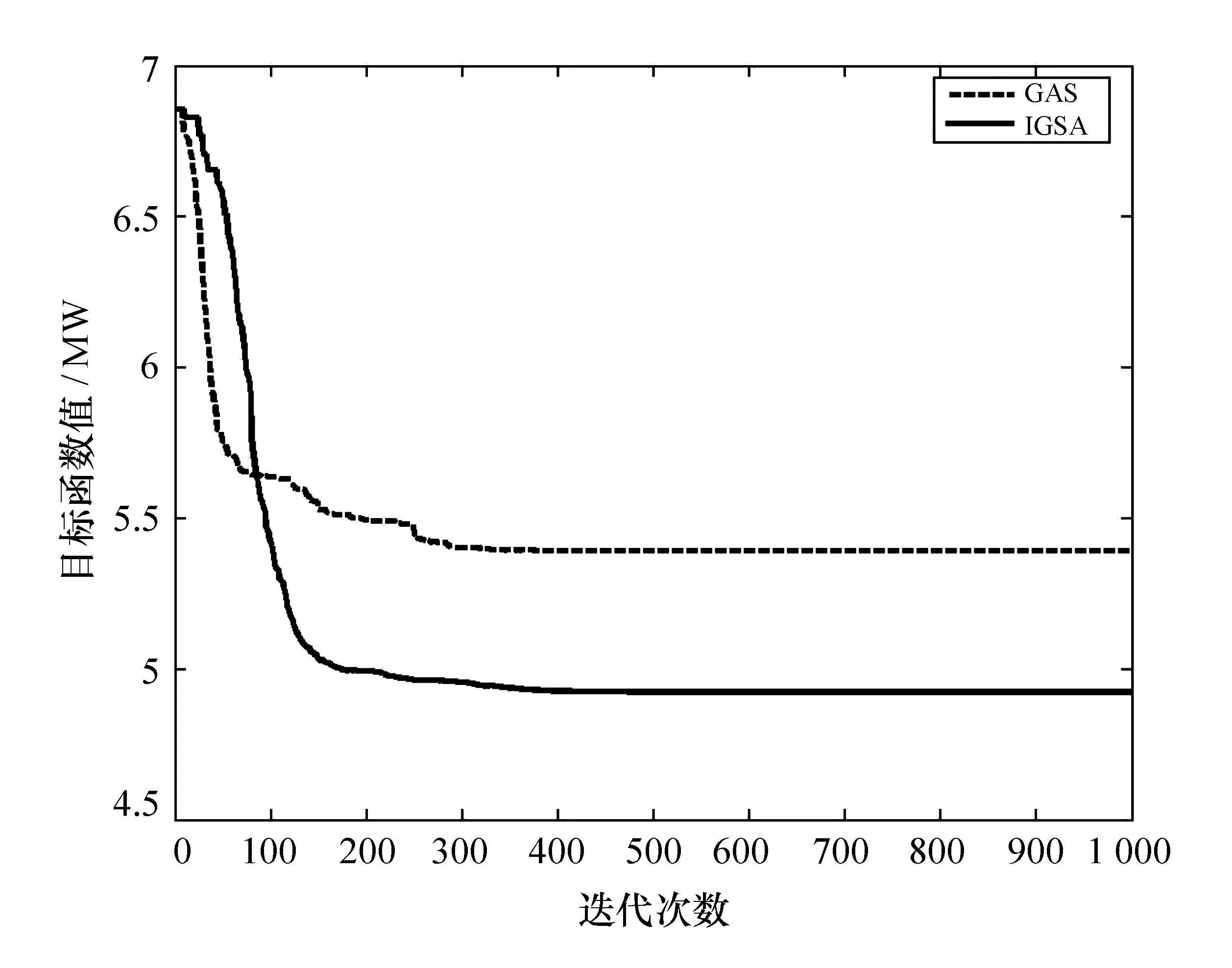
图2　平均收敛曲线

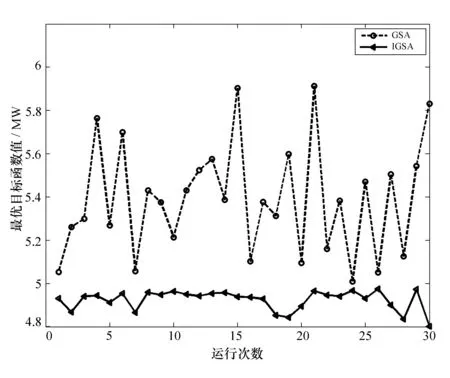
图3　最优结果分布

由图2可知，GSA和IGSA应用于无功优化的求解过程都得到了收敛，但IGSA的优化效果明显优于GSA，IGSA能够搜索到目标值更好的解。GSA在迭代到100代左右就出现了陷入局部最优解的现象，而此时IGSA仍在继续搜索，GSA和IGSA趋于完全收敛分别在350代和500代左右。这说明改进后IGSA有效克服了GSA易早熟和局部收敛能力差的缺点。由图3可知，IGSA中，30次独立实验的最优结果分布更集中，这一点正好与表2中较小的标准偏差是一致的。另外，需要说明的是，两种算法搜索到的所有解都满足约束条件，因此系统可以安全稳定运行。

GSA和IGSA优化得到的最优解，即是无功优化问题中合理分配无功功率以减少系统有功损耗的最优控制变量。GSA和IGSA的最优控制变量如表3所示，表中的数据都是以100MVA作为功率基准值的标幺值。其中，VG1—VG6表示6台发电机的端电压，属于连续变量；T1—T4表示4台变压器的抽头变比，属于离散变量，每个档位取0.02，总共10个抽头；QC1—QC9为9个电容器的无功补偿容量，也属于离散变量，每个档位取0.005，总共10个投切；Cmax和Cmin分别表示控制变量的上限和下限。

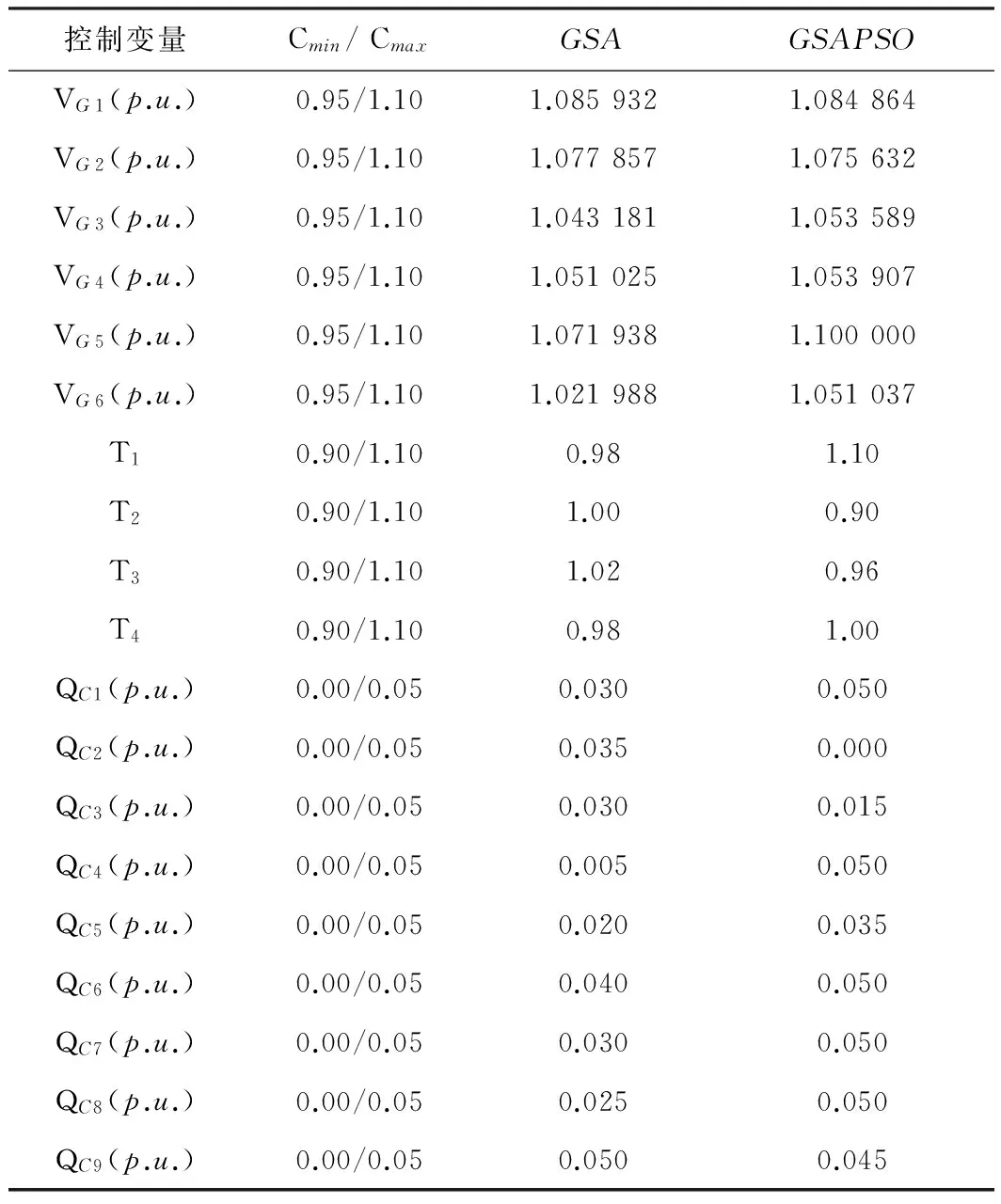
表3　最优控制变量

4　结语

为了解决引力搜索算法(GSA)求解电力系统无功优化易早熟和局部搜索能力差的问题，引入粒子群算法的记忆功能和加速机制，得到了改进引力搜索算法(IGSA)。利用Matlab在IEEE30节点测试结果表明，在系统安全稳定运行的条件下，IGSA避免了早熟现象，增强了局部搜索能力，能获得质量更高的最优解。将理论知识与实践仿真相结合，可加深学生对无功优化和智能算法的理解，提高学生的实践能力，并激发学生的学习兴趣，进而有效提高教学质量。

References)

[1]ChenG,LiuL,SongP,etal.ChaoticimprovedPSO-basedmulti-objectiveoptimizationforminimizationofpowerlossesandLindexinpowersystems[J].EnergyConversionandManagement,2014,86(10):548-560.

[2] 李鹏，徐伟娜，周泽远，等.基于改进万有引力搜索算法的微网优化运行[J].中国电机工程学报,2014,34(19):3073-3079.

[3] 龚安，吕倩，胡长军，等.基于混沌万有引力搜索算法的SVM参数优化及应用[J].计算机科学,2015,42(4):240-243.

[4]DumanS,GüvençU,SönmezY,etal.Optimalpowerflowusinggravitationalsearchalgorithm[J].EnergyConversionandManagement,2012,59:86-95.

[5]KennedyJ,EberhartR.particleswarmoptimization[C]//IEEEInternationalConferenceonNeuralNetworks.Perth,Australia,1995.

[6] 许允之，刘昊，冯宇，等.Matlab在电力系统仿真实验中的应用[J].实验技术与管理,2007,24(1):103-105.

[7] 吕秀丽，牟海维，李贤丽.Matlab在电磁场与电磁波实验教学中之应用[J].实验室研究与探索,2010,29(2):110-112.

[8] 刘金颂，张庆阳，苏晓峰，等.Matlab软件在自动控制原理实验中的应用[J].实验技术与管理,2014,31(6):138-140.

[9]ZimmermanRD,Murillo-SánchezCE,GanD.MATPOWER:amatlabpowersystemsimulationpackage[EB/OL].(2007-09-21)[2015-10-08].http://www.pserc.cornell.edu/matpower/3.2.

[10] 陈功贵，黄山外，郭艳艳，等.基于Simulink的风电机组变桨距控制系统仿真研究[J].实验技术与管理,2015,32(8):105-108.

[11] 史燕.用Matlab改进电子技术课程滤波器实验[J].实验技术与管理,2014,31(12):107-109.

[12] 陈功贵，杜阳维，郭艳艳，等.水轮机调速系统抗负荷扰动的动态仿真研究[J].实验技术与管理,2015,32(6):97-101.

[13]RashediE,Nezamabadi-PourH,SaryazdiS.GSA：AGravitationalSearchAlgorithm[J].InformationSciences,2009,179:2232-2248.

Researchonsimulationofreactivepoweroptimizationbasedonimprovedgravitationalsearchalgorithm

ChenGonggui1,LiuLilan1,GuoYanyan2,GuoFei1

(1.CollegeofAutomation,ChongqingUniversityofPostsandTelecommunications,Chongqing, 400065,China;2.DepatmentofLocomotiveandVehicleEngineering,WuhanRailwayVocationalCollegeofTechnology,Wuhan430205,China)

Gravitationalsearchalgorithm(GSA)iseasytoconvergenceprematurelyandhasthepoorlocalsearchabilitywhensolvingreactivepoweroptimizationproblem.Thus,improvedgravitationalsearchalgorithm(IGSA)isformedbyintroducingthememoryfunctionandaccelerationmechanismofPSObasedonbasicGSA.GSAandIGSAhavebeenexaminedandtestedinIEEE30bustestsystemforsolvingreactivepoweroptimizationbasedonMatlabsoftware.SimulationresultsrevealthatIGSAcanavoidprematurityphenomenon,enhancelocalsearchabilityandobtaintheoptimalsolutionwithhigherquality.Thesimulationexperimentcandeepenstudents'understandingforreactivepoweroptimizationandintelligentalgorithms.

reactivepoweroptimization;improvegravitationalsearchalgorithm;Matlab;simulationofpowersystem

DOI:10.16791/j.cnki.sjg.2016.05.029

2015- 10- 19

重庆邮电大学教育教学改革项目(XJG1522)；重庆市研究生教改项目(yig143061)

陈功贵(1964—)，男，重庆，博士，教授，主要从事电气工程专业的教学和科研工作.

E-mail：chenggpower@126.com

TM732

A

1002-4956(2016)5- 0113- 04