某人工岛大圆筒结构静力稳定性有限元分析

◎ 吴炳奎 广州港工程设计院有限公司



某人工岛大圆筒结构静力稳定性有限元分析

◎ 吴炳奎 广州港工程设计院有限公司

基于某人工岛工程实例，针对其中的大圆筒围堰结构，对其在外部水平荷载作用下的静力稳定性进行有限元分析。通过建立大圆筒结构及其周围土体的三维弹塑性有限元模型，利用加载系数法分析大圆筒与土体的整体稳定性，计算得出结构的稳定性安全系数K=1.53，表明结构安全。同时，分析了结构与土体在设计荷载作用下的变形性状，并探讨了结构在极限状态下的变位及地基破坏模式。

人工岛 大圆筒结构 静力稳定性 有限元分析

1.工程概况

某人工岛东、西两侧分别与海底隧道和引桥衔接，岛上采用现浇隧道结构来完成二者间的过渡，为满足岛上隧道结构的干地施工条件，拟沿人工岛岸线布置插入式钢大圆筒，并在其内、外侧辅以抛石斜坡堤的结构方案。该设计方案典型断面如图1所示，其中大圆筒直径22.0m，壁厚16mm，筒顶高程+3.30m，圆筒底高程为-29.0m～-35.0m。筒内回填中粗砂并振冲密实，筒间净距2.0m，圆筒间副隔舱采用直线型钢板止水连接。大圆筒外侧采用抛石斜坡堤，抛石斜坡堤下部施打挤密砂桩，抛石堤身抛填10～100kg块石，块石与换填中粗砂间设置1.8m厚碎石垫层；抛石堤身外侧坡度为1∶2，外侧设置300～500kg、1.1mm厚块石垫层；外侧采用3t扭王字块护面。堤心石顶部设现浇混凝土挡浪墙，其顶标高+7.5m。

2.大圆筒静力稳定性分析

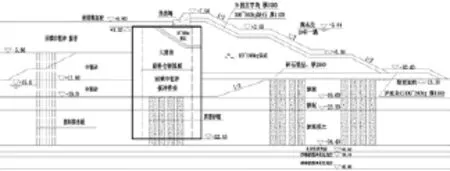
图1　大圆筒结构典型断面

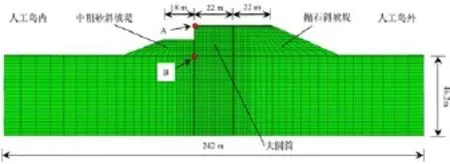
图2　大圆筒结构与土体的有限元模型

本文主要针对图1所示的大圆筒围堰结构，分析其在外荷载作用下的静力稳定性。通过建立大圆筒结构及其周围土体的三维弹塑性有限元模型，利用加载系数法分析大圆筒与土体的整体稳定性。

2.1有限元模型

为提高有限元计算效率，根据大圆筒结构本身及其受力的空间对称性，取一组大圆筒结构的1/2为对象建模，如图2所示。相应的土体计算域取垂直于人工岛岸线轴线方向，并向两侧各取5倍大圆筒直径长度（即总计算域长为110+22+110=242m）；土体在深度方向上取到微风化花岗岩层（共46.2m深）；而大圆筒内、外斜坡堤均进行如图1所示的简化处理。同时，地基表面为自由边界，底面为固定边界，前、后侧面为侧限边界，左、右侧面为对称边界。为了方便有限元建模并保守计算，结构稳定性计算中不考虑大圆筒副格仓，而作用在其上的外荷载一并施加到大圆筒上。同时，由于大圆筒结构由钢材制成，其结构强度和刚度远远大于土体，结构系统的位移和失稳破坏主要决定于地基土的变形和承载能力，故在有限元分析中大圆筒结构采用弹性模型，土体本构模型采用Mohr-Coulomb模型。建模时，土体和结构均采用C3D8R八节点三维减缩积分实体单元。为了很好地模拟土与大圆筒结构的相互作用，建立结构与土体相接触的主从接触面，由于结构的弹性模量远大于土体，故指定结构上的接触面为主接触面，土体上的为从接触面。接触面上的本构模型在切向采用Mohr-Coulomb摩擦本构模型，法向采用硬接触方式。

2.2水文地质条件及外荷载

本文中取10年一遇高水位（+2.84 m）作为计算依据，此时，由于大圆筒结构外部存在抛石斜坡堤，故可认为波浪击打在斜坡堤上便已经发生破碎，因此，波浪力不会直接作用于大圆筒结构上。文中作用于大圆筒上的外荷载主要考虑剩余水压力（水头为2.84+15=17.84m）以及内、外土压力，筒体右侧上按剩余水压力的分布加载至极限状态。同时，根据钻孔的土层分布作为有限元分析的土层断面，其中各层分别为：①换填中粗砂，约5.2m厚，内摩擦角φ=32°，泊松比v=0.25；②挤密砂桩（60％），约15.4m厚，φ=23.6°，泊松比v=0.25；③强风化花岗岩，约7.6m厚，粘聚力c=0.0145MPa，φ=29.6°，v=0.3；④中风化花岗岩，约18m厚，c=0.0145MPa，φ=29.6°，v=0.3。

2.3结构失稳判别标准及加载系数

本文中结构整体稳定性的判断标准为：结构是否由稳定静止状态变为运动状态，出现了整体滑移，滑动面上的位移或应变出现了突变，而且有限元数值计算不再收敛。同时，为清楚表达计算时施加荷载与设计荷载的关系，对荷载加载值进行无量纲化处理，定义一个表征荷载加载程度的加载系数α=P/PD，其中，P为计算时施加的荷载；PD为设计荷载。当P加载到结构极限承载力Pu时，若α＜1，表明结构极限承载力小于设计荷载，不安全；若α=1，表明结构处于极限状态；若α＞1，则表明结构极限承载力大于设计荷载，安全。故当P加载到结构极限承载力Pu时，α也可被定义为结构稳定性安全系数K。为方便分析，取有限元计算得到大圆筒上关键点A、B（如图2）的水平位移数据，通过计算得到大圆筒结构的外荷载-结构转角的变化规律，从而得出结构的稳定安全系数。

2.4结果分析

2.4.1大圆筒结构稳定安全系数计算

经有限元计算得到大圆筒结构在10年一遇高水位的剩余水压力以及内外土压力作用下的外荷载加载系数-结构转角变化规律如图3所示，从中可知大圆筒结构在的安全系数为K=1.53，大于1，表明结构安全。

2.4.2设计荷载作用下大圆筒结构的位移结果分析

图4中展示了在设计荷载作用时，大圆筒结构和地基土整体的位移分布图（左图）以及筒体的位移分布图（右图）。从计算结果中可以看出：对于结构和土整体而言，位移最大值出现在外侧抛石斜坡堤与大圆筒筒壁交界处，此处的最大位移约为0.1099m；而单独的筒体最大位移却只有0.0583m，表明结构系统整体变形主要还是由于斜坡堤自身变位而引起的。综上所述，结合结构整体的安全系数以及所计算得到的位移来看，大圆筒结构的静力稳定满足要求。

2.4.3极限承载力状态时大圆筒结构的位移结果分析

图5（左图）为10年一遇高水位时大圆筒结构在外荷载作用下达到极限承载力状态时地基中塑性变形PE的分布图。从图中可见：在极限状态时，大圆筒内、外的土体自筒底附近到地表处都形成了塑性变形贯通区，内、外侧土体分别发生被动、主动破坏。土体塑性区的分布和大小沿筒基圆周存在空间差异，圆筒弧顶附近土体塑性区的分布范围和数值大小均大于其两侧圆周处，且塑性区主要集中在筒体外侧，筒内土体塑性变形较小。图5（右图）为极限承载力状态时大圆筒筒体的位移场分布图。从图中可看出：大圆筒结构在达到极限状态时，结构在剩余水压力及内外土压力共同作用下的变位模式主要为平动变形。

图3　大圆筒结构的外荷载加载系数随结构AB间转角的变化规律

图4　大圆筒结构在设计荷载作用时的整体位移分布（左图）与筒体位移分布（右图）

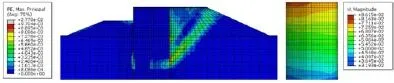
图5　大圆筒结构在极限荷载作用下地基土的塑性应变分布（左图）以及筒体位移分布（右图）

3.结论

本文基于某人工岛工程实例，针对其中的大圆筒围堰结构，对其在外部水平荷载作用下的静力稳定性进行有限元分析。通过建立大圆筒结构及其周围土体的三维弹塑性有限元模型，利用加载系数法分析大圆筒与土体的整体稳定性，计算得出结构的稳定性安全系数K=1.53，表明结构安全。而后，分析了结构与土体在设计荷载作用下的变形性状，对于结构和土整体而言，位移最大值出现在外侧抛石斜坡堤与大圆筒筒壁交界处，且结构系统整体变形主要还是由于斜坡堤自身变位而引起的。同时，探讨了结构在极限状态下的变位及地基破坏模式，在极限状态时，大圆筒内、外的土体自筒底附近到地表处都形成了塑性变形贯通区，内、外侧土体分别发生被动、主动破坏。土体塑性区的分布和大小沿筒基圆周存在空间差异，圆筒弧顶附近土体塑性区的分布范围和数值大小均大于其两侧圆周处，且塑性区主要集中在筒体外侧，筒内土体塑性变形较小。

［1］范庆来，栾茂田，杨庆.软基上沉入式大圆筒结构的水平承载力分析［J］.岩土力学，2004，25（2）：191-195.

［2］王元战，华蕾娜，祝振宇.软土地基条件下大型圆筒海岸结构稳定性计算方法［J］.岩土力学，2005，26（1）：41-45.

［3］王刚，陈杨，张建民.大圆筒结构倾覆稳定分析的有限元法［J］.岩土力学，2006，27（2）：238-241.

［4］JTS 145-2-2013 海港水文规范［S］.

［5］JTS 144-1-2010 港口工程荷载规范［S］.