低复杂度的HEVC码率控制算法

王亦群，杨　静

(上海海事大学　信息工程学院，上海　201306)



低复杂度的HEVC码率控制算法

王亦群，杨静

(上海海事大学信息工程学院，上海201306)

针对HEVC视频编码中帧层比特分配和率失真模型参数自适应更新，提出了一种改进的码率控制算法。该算法引入牛顿法来自适应更新率失真模型的参数；同时提出一种帧层复杂度度量方法，利用图像自身的内容特性来调整帧层比特分配；最后在编码过程中选择合适的量化参数。实验结果表明：与参考算法比较，该算法能大大降低计算复杂度，同时保持良好的码率控制性能，对含有场景突变的视频改进效果尤为明显。

HEVC；码率控制；牛顿法；场景切换；计算复杂度

随着高清、超高清视频的大量涌现，对网络带宽提出了更高的要求。因此，国际电联(ITU-T)、国际标准化组织(ISO)、国际电工委员会(IEC)联合发起联合视频编码小组(Joint Collaborative Team on Video Coding，JCT-VC)制定下一代的视频编码标准HEVC(High Efficiency Video Coding)，相比H.264/AVC视频压缩标准有显著提高，在相同的视觉质量下能节省约50%的比特率[1]。在实时传输中，如果编码器输出的码流比特数过大，会导致输出缓冲区上溢，进而使视频传输延迟、出现视频序列间断等情况；而如果码流比特太小，会导致视频质量下降。为了使编码输出的比特率与通信带宽相适应和得到更好的视频图像质量，需要使用码率控制算法根据带宽动态地调整编码器的编码参数。

目前HEVC码率控制策略是H0213算法[2]和基于R-λ模型的K0103算法[3]，其他的码率控制策略对这些模型做了一些改进。2012年的JCT-VC会议上，Li Bin提出基于R-λ模型的K0103提案，能获得较好的编码质量，且较好地控制码率精度，然而K0103提案中帧层比特分配并没有考虑不同视频的内容特性。码率控制算法应该根据不同的视频内容特性，来合理地为编码器选择编码参数，使实际编码码率与目标码率尽量保持一致。一些码率控制算法使用差分直方图度量图像复杂度，对于不同的视频序列，阈值的选择具有不确定性[4]；史久根等人提出复杂度测度因子由加权MAD值和阈值共同决定，也要进行阈值选择[5]；还有人提出基于像素的相异度量来度量图像复杂度，利用了帧层像素的标准差和均值，计算量较大[6]。面对含有场景切换的视频编码情况，胡乾乾等人提出及时终止当前GOP，并且插入I帧[7]，这种编码方式对于场景切换频繁的序列，可以有效提高视频重现质量，但是插入I帧往往使实际码率的匹配度降低。

因此，本文针对HEVC率失真模型α和β参数的更新和帧层码率控制的比特分配，提出了一种改进的低复杂度HEVC码率控制算法。首先利用牛顿法进行率失真模型参数的自适应更新，能够大大降低计算复杂度。同时，利用图像复杂度度量方法对帧层比特进行自适应分配，获得较好的视频重现质量。

1　改进的HEVC码率控制算法

1.1自适应更新率失真模型参数

1.1.1率失真模型

目前，HEVC参考软件HM中采用的是Li Bin等人提出的基于R-λ模型的码率控制算法[8]。其中λ是拉格朗日乘子，表示为率失真曲线的斜率，R-λ模型如下

(1)

式中：α和β是和编码视频有关的参数，可以随着编码过程不断更新；R是当前编码帧或编码单元的目标比特；D(R)是跟码率R有关的编码失真；C和K是两个与编码失真有关的参数。

JCTVC-K0103采用梯度下降法来更新模型参数，其计算过程复杂，因此本文引入牛顿法来进行参数更新。

1.1.2使用牛顿法自适应更新模型参数

牛顿法用于最优化问题的基本思想是：在极小点附近通过对目标函数做二阶泰勒展开，求使目标函数一阶导为零的点，即极小点的估计值[9]。考虑最简单的一维情况，假若目标函数为f(x)；初始迭代点为x0；其牛顿法的迭代公式为式(2)。牛顿法具有二阶收敛性，在二阶导数的作用下，运算更加精确、快速。

(2)

式中：xn和xn+1分别为第n次和第n+1次的迭代点；f′(xn)是在xn点处目标函数的一阶导数；f″(xn)是在xn点处目标函数的二阶导数。在提案JCTVC-K0103中R-λ模型的α和β参数更新是基于梯度下降法实现的，使用式(3)和(4)实现的，其计算复杂度较高。

αnew=αold+δα·(lnλreal-lnλcomp)·αold

(3)

βnew=βold+δβ·(lnλreal-lnλcomp)·lnbpp

(4)式中：αold和βold均为前一个迭代点的率失真模型参数；αnew和βnew都是当前迭代点的率失真模型参数；δα和δβ分别是率失真模型中参数α和参数β的迭代步长；bpp是每像素消耗比特数；λreal是码率分配算法产生的拉格朗日乘子；λcomp是编码过程中实际的比特数，通过式(1)计算得出的拉格朗日乘子。本文使用牛顿法对率失真模型参数进行更新，计算方法更加简单。在已知αold，βold，bpp和λreal的情况下，根据式(1)可以得出实际的λreal值与计算的λcomp值，用式(5)和(6)来更新α和β参数

αnew=αold+αold·(lnλreal-lnλcomp)

(5)

βnew=βold+(lnλreal-lnλcomp)/lnbpp

(6)

使用牛顿法更新α和β参数的方法推导如下，目标函数e2为实际的λreal值与计算的λcomp值间的平方误差，用式(7)表示

e2=(lnλreal-lnλcomp)2=(lnλreal-lnα-β·lnbpp)2

(7)

并对lnα和β分别求一阶导和二阶导，得出式(8)和(9)

(8)

(lnbpp)2

(9)

利用牛顿法进行迭代，根据式(2)可得式(6)和式(10)。最后将式(10)取e指数，接着进行泰勒展开，忽略其二阶项及高阶项，可得式(5)。

lnαnew=lnαold+lnλreal-lnλcomp

(10)

梯度下降法一般会比牛顿法迭代的次数更多，又需要考虑每次迭代的步长，步长过小则迭代次数多，步长过大易产生振荡效果。使用牛顿法既不需要考虑步长，而且迭代次数又少，计算复杂度较低。

1.2自适应帧层目标比特分配

提案JCTVC-K0103算法在帧层采用分级分配比特的方法，图像复杂度用权重ω表示，按照权重所占的比例进行分配比特，但该算法未考虑图像自身的纹理复杂度和运动特性。因此，本文提出了一种基于像素统计的帧层复杂性度量方法，并将视频序列分为两种不同的编码情况，进行帧层比特分配。在给定目标比特率Rtar和帧率f的情况下，K0103算法由式(11)分配帧层比特数

(11)

式中：TCurrPic是当前帧的分配比特数；TGOP是当前GOP的分配比特数；CodedGOP为GOP中已经编码的比特数；ωCurrPic是当前帧的分配比特权重；ωi是所有GOP中所有未编码图像分配比特的权重。

改进的帧层图像复杂度度量方法是使用基于像素统计的方法，先求出前后两帧图像中所有像素点的亮度差的平均值，然后再平方得到复杂度因子B(n)，用式(12)表示

(12)

因此，帧层比特分配调整为式(13)

(13)

式中：pn(i,j)和pn-1(i,j)分别为第n帧与第n-1帧(i,j)位置的亮度分量值；M和N分别是图像的宽和高；TCurrPic是当前帧的目标比特；TGOP是当前GOP的目标比特；Bi是未编码图像的复杂度因子；BCurrPic是当前帧的复杂度因子；CodedGOP是当前GOP中已编码比特数。

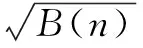
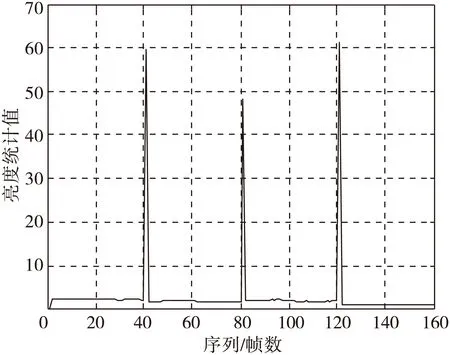
图1　合成序列min720各帧复杂度变化趋势

当测试序列为连续视频序列时，帧层比特分配策略采用式(12)和(13)，利用视频内容特性来分配比特，能更好地反映视频的真实情况。

当测试序列含有场景突变时，首先在场景切换处及时终止GOP层编码，同时调整率失真模型参数，将α和β初始化分别为3.200 3和-1.367。然后，场景切换帧按I帧编码，场景切换的下一帧仍按P帧编码，它们帧层的比特分配策略与上述情况相同。

1.3量化参数的选择

帧层比特编码的实现需要确定拉格朗日乘数λ的值，然后根据率失真模型(RDO)选择包括量化参数QP在内的合适编码参数。QP的编码过程分为两种情况：1)当测试序列为连续视频序列时，利用前一编码帧的比特反馈值μ及时调整当前帧的量化参数QP。前一帧的实际编码比特与目标比特的比值作为调整因子μ，由式(14)计算得到，再根据μ对当前帧的QP按式(15)进行微调整。2)当测试序列含有场景突变时，先将场景切换帧的量化参数QP加2，接着再利用调整因子μ按式(15)选择QP的大小。

(14)

(15)式中：μ为前一帧的比特反馈值；Ri(j-1)是前一帧的实际比特数；Ti(j-1)是前一帧的目标码率；QP为量化参数。

2　仿真结果与分析

本文提出的码率控制算法是在参考软件HM10.0按低延时IPPP的配置下实现的。实验中用到3个含有场景切换的测试序列和6个连续视频序列。3个含有场景突变的视频序列均为160帧，由不同序列拼接组成mix1 080，mix720，mix480序列。BasketballDrill，Kimono，Cactus和ParkScene，分辨率为1 920×1 080，帧率是50 f/s，各40帧组成mix1 080序列。FourPeople，KristenAndSara，Johnny和Vidyo1，分辨率为1 280×720，帧率是60 f/s，各40帧组成mix720序列。PartyScene，BQMall，BasketballDrill和RaceHorses，分辨率为832×480，帧率是30 f/s，各40帧组成mix480序列。这些序列都含有复杂的场景，如图1的第41、第81和第121为场景切换帧。6个连续视频序列分别是BQTerrace和Tennis是分辨率为1 920×1 080的100帧视频序列，FourPeople和Johnny是分辨率为1 280×720的100帧视频序列，BQMall和BasketballDrill是分辨率为832×480的100帧视频序列。本文以HEVC Call for Proposal(CFP)中规定的码率作为码率控制技术的目标码率[10]，使用这些目标码率值进行仿真。

为了验证使用牛顿法的码率控制算法的编码性能，对6个不同分辨率及运动特性的视频进行仿真，结果如表1所示。从表1中可知，使用牛顿法可以在比特精确度和PSNR与K0103算法大致相同的情况下，大大减少计算复杂度。与K0103算法相比，最多能节省6.09%的时间。

表1牛顿法的码率控制算法与K0103码率控制算法编码结果比较

测试序列目标比特率/(kbit·s-1)牛顿法K0103算法牛顿法与K0103算法比实际比特率/(kbit·s-1)比特率误差/%PSNR/dB时间/s实际比特率/(kbit·s-1)比特率误差/%PSNR/dB时间/s比特率精度提高/%ΔPSNR/dB时间节省/%BQTerrace(1080p)10000100200.20035.1054875.410012.080.12135.2358433.7-0.079-0.136.0970006986.490.19334.6554543.46997.330.03834.7356544.6-0.155-0.083.54Tennis(1080p)100009998.60.01441.3585121.39980.980.19041.4185919.80.176-0.060.9370007011.740.16840.5876687.86973.370.38040.6276834.90.213-0.040.19FourPeople(720p)40003995.570.11142.8221880.33986.440.33942.7622565.70.2280.063.0420002012.520.62641.7518245.51997.880.10641.6419102.1-0.5200.114.48Johnny(720p)40003978.380.54043.1025154.33984.240.39443.1025881.1-0.1460.002.8120002007.310.36542.2819810.81997.730.11342.2220058.2-0.2520.061.23BQMall(480p)20001993.620.31935.1923348.11999.20.04035.2423928.7-0.279-0.052.4312001202.520.21033.0822335.91199.260.06233.0922805.9-0.148-0.012.06BasketballDrill(480p)20002005.700.28538.2924470.92000.700.03538.1824567.2-0.2500.110.3912001205.690.47436.3023769.61200.990.08336.1824010.2-0.3920.121.00平均值—————————-0.1340.011.38

为了验证改进的低复杂度码率控制算法的编码性能，对3个含有场景突变的视频序列进行仿真，将实验结果与胡乾乾的码率控制算法(Hu算法)[7]以及K0103码率控制算法进行比较，仿真结果如表2所示。从表2可知，本文算法与Hu算法相比，比特精确度大大提高，高达2.54%；大多数情况下，测试序列的峰值信噪比PSNR也均有提高。然而采用了改进的帧层分配比特方法与牛顿法的结合，增加了复杂度因子的计算，使计算复杂度与Hu算法相比有所提高。本文算法与K0103算法相比，在比特精确度和PSNR大致相同的基础上，大大降低了计算复杂度，平均编码时间节省10.60%。

图2是mix720测试序列在目标码率为512 kbits/s时，每一帧的PSNR对比图。从图2中可知，由于在帧层码率分配时考虑了图像复杂度，本文算法较其他两种算法，有较好的码率稳定性，PSNR的方差更小，视觉感受更加平滑。图2中，本文算法、Hu算法与K0103算法的峰值信噪比PSNR的标准差分别是1.309，1.899，2.142；均值分别为38.12，37.78，37.79。

表2本文码率控制算法与Hu算法及JCTVC-K0103的码率控制算法编码结果比较

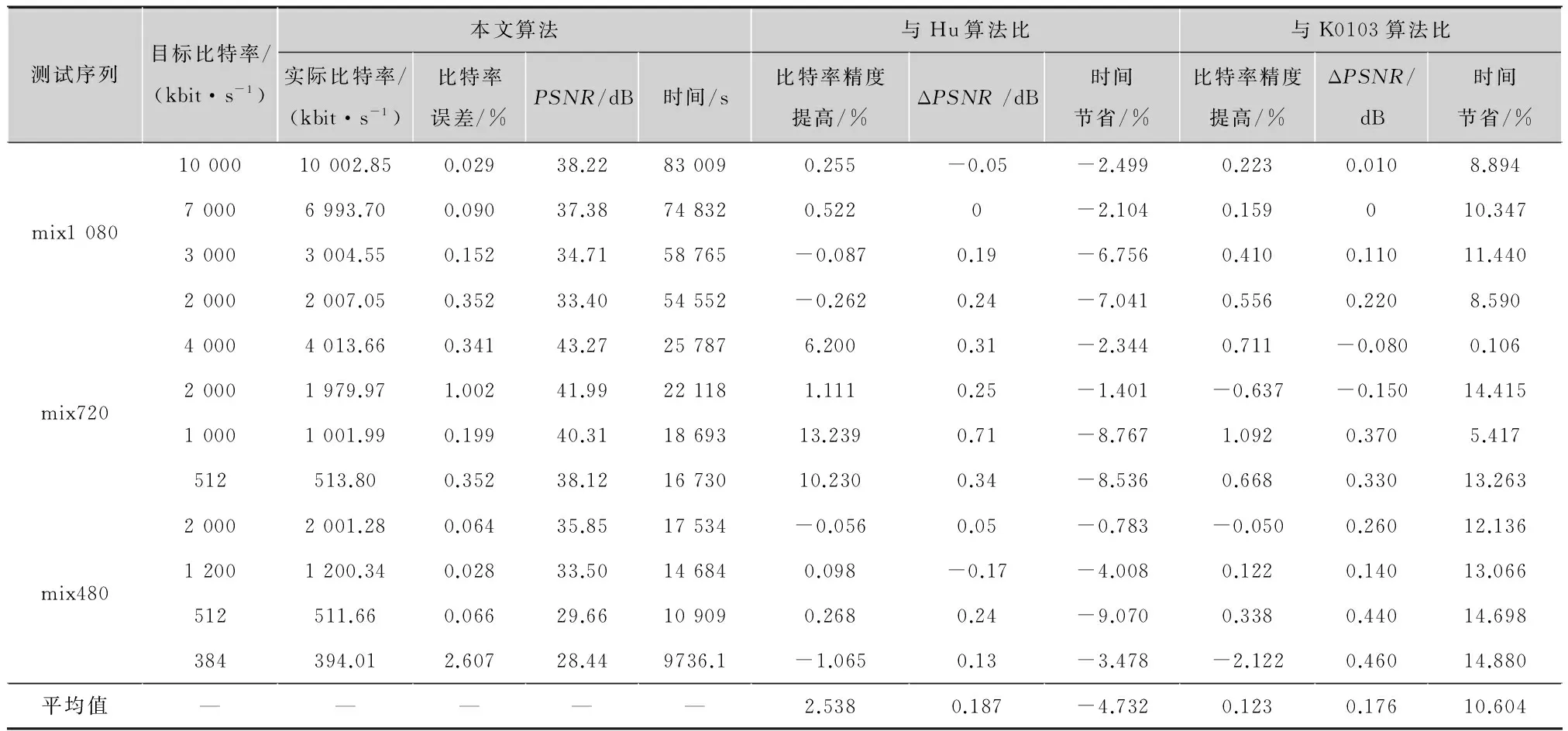
测试序列目标比特率/(kbit·s-1)本文算法与Hu算法比与K0103算法比实际比特率/(kbit·s-1)比特率误差/%PSNR/dB时间/s比特率精度提高/%ΔPSNR/dB时间节省/%比特率精度提高/%ΔPSNR/dB时间节省/%mix10801000010002.850.02938.22830090.255-0.05-2.4990.2230.0108.89470006993.700.09037.38748320.5220-2.1040.159010.34730003004.550.15234.7158765-0.0870.19-6.7560.4100.11011.44020002007.050.35233.4054552-0.2620.24-7.0410.5560.2208.590mix72040004013.660.34143.27257876.2000.31-2.3440.711-0.0800.10620001979.971.00241.99221181.1110.25-1.401-0.637-0.15014.41510001001.990.19940.311869313.2390.71-8.7671.0920.3705.417512513.800.35238.121673010.2300.34-8.5360.6680.33013.263mix48020002001.280.06435.8517534-0.0560.05-0.783-0.0500.26012.13612001200.340.02833.50146840.098-0.17-4.0080.1220.14013.066512511.660.06629.66109090.2680.24-9.0700.3380.44014.698384394.012.60728.449736.1-1.0650.13-3.478-2.1220.46014.880平均值—————2.5380.187-4.7320.1230.17610.604

图2　mix720序列在目标码率为512 kbit/s时的Y-PSNR对比图

3　结论

本文首先分析了K0103码率控制算法的率失真模型，然后针对率失真模型参数α和β更新算法较繁琐以及帧层比特分配未考虑图像复杂度，本文提出了一种改进的低复杂度码率控制算法。实验结果证明了利用了牛顿法更新模型参数，能够大大降低计算复杂度，获得较好的编码效果；帧层复杂度度量方法能够利用视频自身的内容特性，自适应分配帧层比特，最终获得更平滑的视频质量。

[1]SULLIVAN G J， OHM J R， HAN W J， et al. Overview of the high efficiency video coding(HEVC) standard[J]. IEEE transactions on circuits and systems for video technology， 2012， 22(12)：1649-1668.

[2]CHOI H， NAM J， YOO J， et al. Rate control based on unified RQ model for HEVC[C]//Proc. JCT-VC of ITU-T SG16 WP3 and ISO/IEC JTC1/SC29/WG11 8th Meeting. [S.l.]：JCTVC，2012：56-62.

[3]LI B， LI H， LI L， et al. Rate control by R-lambda model for HEVC[C]//Proc. JCT-VC of ITU-T SG16 WP3 and ISO/IEC JTC1/SC29/WG11 11th Meeting. Shanghai：2012：102-107.

[4]SU L， GUO Y， FAN C， et al. A novel H.264 rate control algorithm for scene transition video[C]//Proc. Automatic Control and Artificial Intelligence (ACAI 2012). Xiamen：IET，2012：220-223.

[5]史久根，许林，张超. 一种场景自适应的H.264帧层码率控制算法[J]. 计算机应用研究， 2010， 27(5)：1968-1969.

[6]TU Q，GUO X，MEN A， et al. A frame-level HEVC rate control algorithm for videos with complex scene over wireless network[C]//Proc. 2014 IEEE 79th Vehicular Technology Conference(VTC Spring). Seoul：IEEE， 2014：1-5.

[7]胡乾乾，沈礼权，赵振军. 基于场景切换的HEVC码率控制算法[J]. 电视技术， 2015， 39(5)：1-3.

[8]LI B，LI H，LI L，et al. λ domain rate control algorithm for high efficiency video coding[J]. IEEE transactions on image processing，2014，23(9)：3841-3854.

[9]Newton′s method in optimization[EB/OL]. [2015-12-10]. https：//en.wikipedia.org/wiki/Newton%27s_method_in_optimization.

[10]WIEGAND T，OHM J R，SULLIVAN G J， et al. Special section on the joint call for proposals on High Efficiency Video Coding (HEVC) standardization[J]. IEEE transactions on circuits and systems for video technology， 2010， 20(12)：1661-1666.

责任编辑：时雯

Low complexity HEVC rate control algorithm

WANG Yiqun，YANG Jing

(CollegeofInformationEngineering，ShanghaiMaritimeUniversity，Shanghai201306，China)

In view of HEVC video coding frame-layer bits allocation and parameters of rate-distortion model adaptively updated，an improved rate control algorithm is proposed. It adaptively updates rate-distortion model parameters by Newton method. In the meanwhile，it adopts a frame-layer complexity metric method and takes full advantage of image content features to adjust frame-layer bits allocation. Finally， the appropriate quantization parameter is selected during the encoding process. The results show that：compared with the reference algorithm， the proposed algorithm greatly reduces the computational complexity and achieves a good rate control performance， particularly for video sequences containing scene changes.

HEVC；rate control；newton method；scene change；computational complexity

TN919.81

ADOI：10.16280/j.videoe.2016.07.002

国家自然科学基金项目(61401270)

2016-01-21

文献引用格式：王亦群，杨静.低复杂度的HEVC码率控制算法[J].电视技术，2016，40(7)：6-10.

WANG Y Q，YANG J.Low complexity HEVC rate control algorithm[J].Video engineering，2016,40(7)：6-10.