应用数字高程模型计算土方量的误差估计
崔晨耕
(西安航空职业技术学院 电子工程学院,陕西 西安 710089)
应用数字高程模型计算土方量的误差估计
崔晨耕
(西安航空职业技术学院 电子工程学院,陕西西安710089)
数字高程模型(DEM)是在一定范围内通过规则格网点描述地面高程信息的数据集,用于反映区域地貌的空间部分,它是国家基础地理信息数字成果的主要组成部分。DEM作为地球表面地形的数字描述和模拟已成为空间数据基础设施和“数字地球”的重要组成部分,已成为独立标准的基础产品,并越来越广泛地被用来代替传统地形图中等高线对地形的描述。传统测绘产品的质量评价体系不能保证合理地对DEM产品进行质量评价,文章通过对应用数字高程模型计算土方量的误差分析,对DEM的误差进行了研究并详细推导出误差计算公式,对土方量计算的误差分析具有重要的意义。
DEM;土方量;误差估计;误差分析
0 引言
DEM最早应用于土木工程领域,可大量节省内外业工作量,所有计算由计算机完成,能使估算过程达到自动化和规范化。准确的土方量计算无疑会提高作业的效率,最终获得最大的经济效益。在市场经济条件下,工程单位愈加注意计算所得土方量的误差大小,可为生产实践提供科学合理的质量标准。传统的土方量计算方法有多种,常用的有断面法、方格网法、散点法和表格法。每种方法都有它的不足之处,总体来讲就是数据采集方式机械且繁琐,数据采集量大,对实际地面的起伏变化描述不能够满足精度要求等。由于其存在着诸多缺点,进而导致最终所建立的模型失真,这也就使得最后所计算出来的结果不能满足高精度土方量计算的要求。就目前的土方量计算研究现状,本论述对数字高程模型计算土方量计算进行误差估计。
1 土方量计算的基本原理
土方量计算有给定设计标高和不给定设计标高两种:后者是指对于一个区域,进行场地平整时,不对外产生挖、填方量,可用程序计算场地平整后的标高和绘制挖填平衡线。给定设计标高又分两种:一种是设计标高固定,设计平面为水平面;另一种是设计标高是变动的,设计平面为一个倾斜面或几个倾斜面的组合,均可用程序建立设计面的平面方程,用设计平面与数字高程模型相切,计算每个格网内的方量,汇总得到整个区域的挖、填方量和总方量。由DEM来计算土方量是根据实地测定的地面点坐标和设计高程,通过生成三角网来计算每一个三棱柱的填挖方量,最后累计得到指定范围内填方和挖方的土方量。如果将DEM视为空间的曲面,填挖前后的两个DEM即为两个空间曲面,那么计算机便可以自动计算两个曲面的交线,也可以用一个铅垂面同时对两个曲面任意切割,并计算夹在两个切割下来的曲面间的空间体积,实际上就是土方计算的填挖交界线、填方量和挖方量。
实践中应用较多的是规则格网DEM,为了方便,讨论较多的是在规则格网情况下土方量的量算及误差估计。在规则格网DEM情况下DEM体积由四棱柱体积进行累加得到,四棱柱体上表面用双曲抛物面拟合。曲面的平均高程为:,其中a为格网边长。ZP可由双线性内插求得。
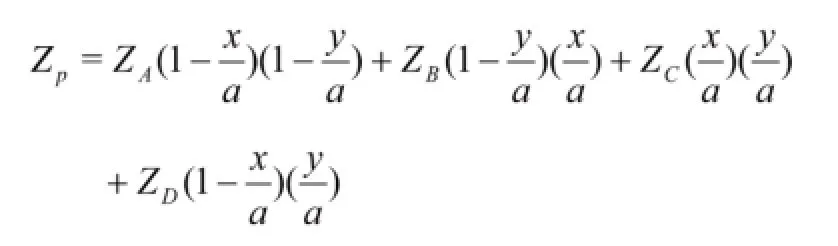
ZA、ZB、ZC、ZD为格网四个角的高程。于是积分可得,得到后可计算挖填方量
S为四棱柱的底面积,H为我们要达到挖填后的平面的高程。
2 土方量的误差估计
土方量总体估计中存在两类误差:
(1)由于地形的复杂性引起的对平均高程估计的误差;
(2)由于底面边界的不确定性引起的误差。
2.1对总体平均高程估计的误差分析
分析双线性建模过程中的误差传播及线性表达地形导致的精度损失,可得到以下公式:
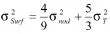
2.1.2平均高程误差的总体估计
i.对研究域V的平均高程Z(V)的总体估计。
ii.总体估计方差
在规则格网情况下有:
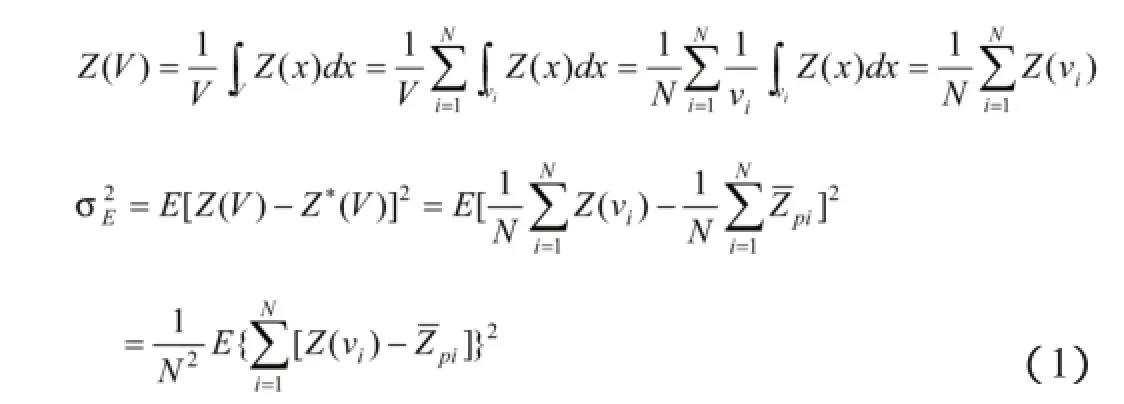

故(2)式为

2.1.3两点说明
i.公式(3)为近似估计,当N较大时近似程度较好。通常进行土石方量算时该条件可以满足。
ii.公式(3)为总体估计方差不同于概率统计中的样本平均数的方差。
2.2底面面积估计的误差分析
2.2.1面积S的总体估计
令k(x)为待估面积的指示函数
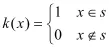
s为待估区域,x为二维空间的点
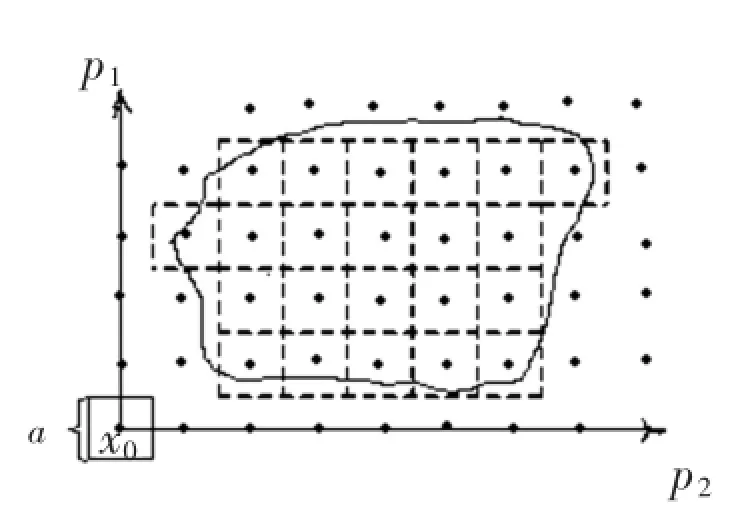
图1 数字高程格网
有面积的估计量为
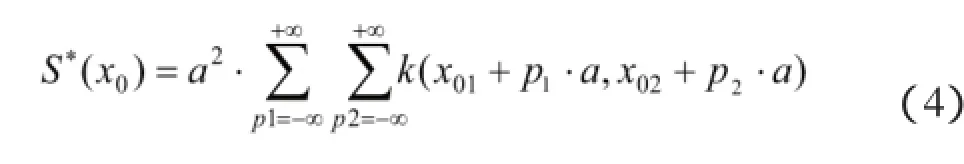

p1,p2为网格序数,(X01,X02)为坐标原点,见图1所示。若用N(x0)表示的格网数目,面积的估计量为

2.2.2S的总体估计方差
由公式(4)可知S的估计量S*(x0)是依赖于x0的位置的,对于每一个新的网格原点,都有一个相应的S的估计量。所以确定估计量误差的一个可能途径就是算出当网格原点X0在基本格网面积a2中取各种可能位置时的平均值。可记为
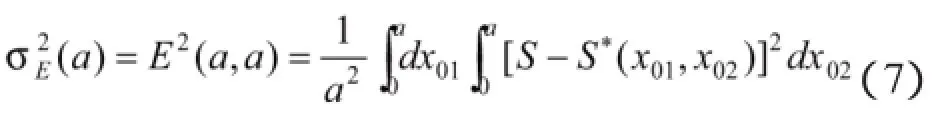
容易证得S*(x0)的数学期望就是S,于是公式(5)进行转化并简写为一维的形式
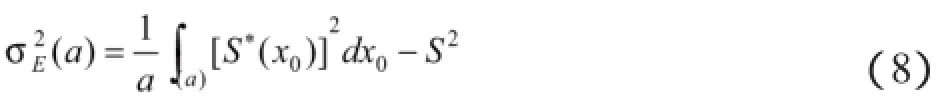
运用公式(5)对公式(8)进一步进行转化可得
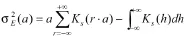
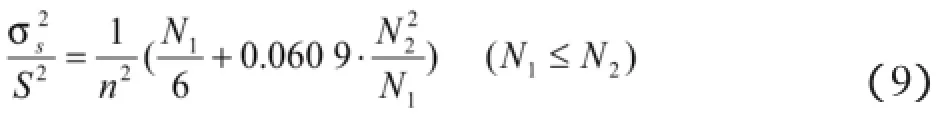
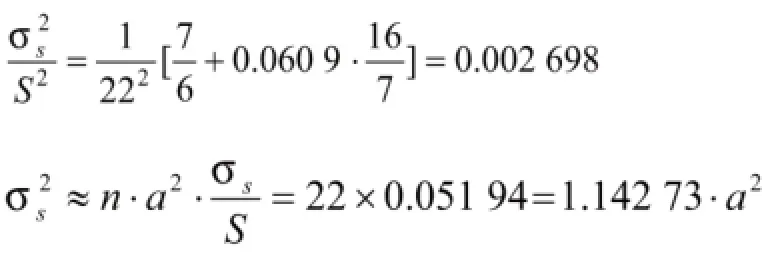
1.96σS=1.96*1.14273*a2≈2
所以面积S的置信度为95%的置信区间为[20*a2,24*a2]。
2.3土方量的总体估计方差
由土方量计算公式V=S*(H-m)S为底面面积,H为平均高程,并假设两者不相关。根据方差协方差传播律有为平均高程误差的总体估计方差,为底面面积总体估计的方差。S可用S*近似代替,H可用近似代替。
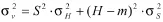
3 结束语
基于DEM的土方量计算实现了土方量计算的计算机自动化,通过软件可以针对不同地形生产各种DEM产品,且误差都符合国家标准的要求,但不同软件对于不同地形在精度上存在一定的差异。所以在计算土方量时,必须根据实际情况,选择合适的DEM产品。
通过分析我们可以得知土方量总体估计误差取决于以下几个方面的因素:
(1)原始数据的精度,采点密度(格网大小);
(2)地形的复杂度;
(3)内插方法的选择;
(4)要进行挖填地的底面曲线的复杂度。
对应用规则格网DEM进行土方量计算在实践中已应用很广泛,但对其进行误差分析并不多见,所以针对这一问题展开的探讨是有实践和理论意义的。
[1] 李志林,高庆.数字高程模型[M].武汉:武汉大学出版社,2011.
[2] 胡鹏.新数字高程理论、方法、标准和应用[M].北京:测绘出版社,2007.
[3] 林宗坚.地图扫描采样分辨率的研究[J].测绘科学,2000,25 (01):13-15.
[4] 崔希璋,等.广义测量平差[M].武汉:武汉测绘科技大学出版社,2001.
[5] 戴洪磊.矢量GIS中位置不确定性度量与传播的理论和方法[D].武汉:武汉测绘科技大学,2000.
[6] 黄加纳,蓝悦明,覃文忠.地图数字化的坐标转换及数据的精度与相关性[J].武汉大学学报(信息科学版),2001(03).
[7] Zhilin Li.et.al.An integrated Technique for automated generalization of contour maps[J].The Cartographic Journal,2000,37(01):29-37.
TU751
A
10.3969/j.issn.1672-6375.2016.07.028
2016-4-9
崔晨耕 (1980-),男,汉族,陕西杨凌人,硕士,讲师,主要研究方向:建筑智能化、航空摄影测量与遥感。

