电子对抗对空侦察雷达阵地配置优化研究

郭　强，高建军，张弓胤

（防空兵学院，郑州　450052）

电子对抗对空侦察雷达阵地配置优化研究

郭强，高建军，张弓胤

（防空兵学院，郑州450052）

针对电子对抗对空侦察雷达阵地优化配置问题，通过分析雷达站的侦察范围与定位条件，提出双机定位和三机定位的最优配置模式，分别建立双机定位和三机定位的最优站距、定位纵深、配置间隔、阵地高度等相关参数的计算模型。通过对电子对抗对空侦察雷达阵地优化配置问题进行实例计算，表明模型实用、有效。

电子对抗，雷达，定位，配置，优化

0　引言

雷达侦察是利用雷达侦察设备搜索、截获敌方雷达辐射的电磁信号，经过分析识别，从中获取战术技术参数及位置数据等情报的活动。雷达侦察是获取侦察情报的重要手段，也是遂行电子对抗的基础。它的主要功能是：①侦察敌雷达信号载频、信号波形、脉冲宽度、脉冲重复频率、信号强度及雷达天线极化方式、波束宽度、扫描方式和速率等雷达特征参数；②测定雷达信号到达方向或对雷达定位；③对所获的雷达特征参数和位置参数进行分析处理，查明敌方雷达的类型、用途、配置情况，从而进一步推断敌方的部署、武器系统配系、威胁程度和行动企图等。

电子对抗对空侦察雷达阵地的科学部署是有效获取侦察区域内雷达电子技术设备及其载体情报的重要条件。对空侦察雷达阵地的部署必须将己方的各种雷达阵地及雷达干扰站统一布局，才能合理地使用兵力和装备，构成严密的电子侦察网，发挥侦察装备的整体最佳效能。

1　雷达侦察站的侦察范围与定位

电子对抗对空侦察雷达站在各个方向上对目标的最大侦察距离轨迹所围成的区域，叫作雷达侦察站的侦察范围。实际中由于受地球曲率和气象条件的限制，在对流层正常折射的情况下，微波以上频段电波近似直线传播，雷达对侦察目标的最大侦察距离r通常按式（1）计算，如图1所示。

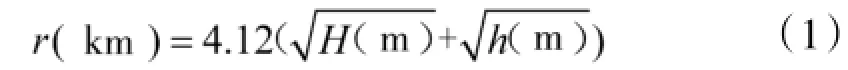
式中：H为侦察站天线中心与地平面相对高度；h为被侦察目标的雷达天线中心与地平面的相对高度。

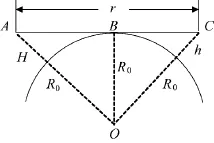
图1　地球曲率对雷达侦察距离的影响

对空雷达侦察站的配置是雷达对抗部（分）队部署的基础。由于单个雷达侦察站的探测定位能力受到其工作带宽、瞬时带宽、工作视野、瞬时视野、可处理的信号类型、可适应的信号流密度、工作灵敏度和动态范围等多种因素的影响，具有较大的不确定性。因此，单个雷达侦察站的探测定位能力十分有限。雷达侦察站的侦察范围，必须能覆盖需要侦察的地域。需要侦察的区域被一个站的侦察范围所覆盖时，称为单层覆盖区域；被两个或数个站的侦察范围所覆盖时，称为双层或多层覆盖区域。一般地，在单层覆盖区域内，只能侦察雷达技术参数；在双层或多层覆盖的区域内，可以进行交会定位。为充分发挥雷达侦察站的性能，必须能同时保证参数侦察和交会定位，力求构成双机或三机最优的有效侦察定位区域。

2　双机定位时雷达侦察站的配置

2.1双机定位的配置模式

为保证双机定位的准确性，定位线的交角不应超过30°～150°的范围，符合这一条件的地方，称为双机可定位区域或双机有效定位区域。

可定位区域面积的大小Am，取决于两侦察站A、B之间的距离lAB以及两雷达站的侦察距离rA、rB，如图2所示。

图2　雷达侦察站双机定位有效定位区域

2.2双机定位最优配置的参数计算

2.2.1双机定位雷达侦察站的最优站距

假定两雷达站的侦察距离相同，即rA=rB=r，设lAB=xr，可解得可定位区域面积

当lAB=0.625 r时，可定位区域面积取最大值：

此时lAB=0.625 r称为最优站距。不能定位的弧形区域高度：

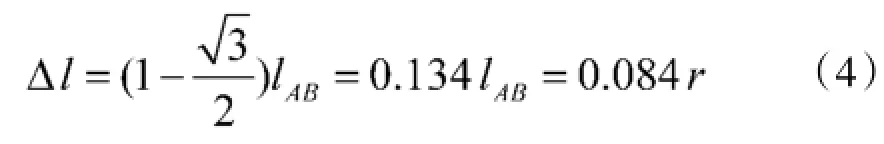
若两雷达站侦察距离不同，假定rA＞rB，记：

在实用范围内（1＜K＜1.75），最优站距可按以下逼近公式计算：

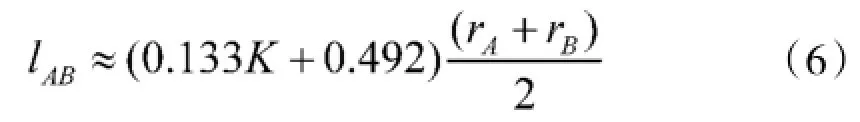
2.2.2双机定位雷达侦察站的定位纵深

双机定位雷达侦察站的有效定位区域的边界线上各点与侦察基线（两个站点的联线）的垂直距离叫作有效定位纵深，记为Y。它受限于低站的侦察距离rB，。提高有效定位纵深的关键在于提高低站的侦察距离rB，进而须提高低站的高度HB，如图3所示。

图3　雷达侦察站双机定位有效定位纵深

当Y=rB时，

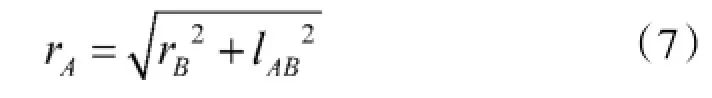
联立式（5）～式（7），可解得K=1.242。

侦察站的实用定位纵深N=Y-Δ l。可计算，当K=1时，Δ l=0.084 r，0.37 r≤Y≤0.95 r，平均有效纵深Y=0.66r，实用定位纵深N满足：0.286 r≤N≤0.866 r，平均实用纵深N=0.576 r；当与友邻站协同定位时，Y=0.865 r，N=0.781 r。

3　三机定位时雷达侦察站的配置

3.1三机定位的配置模式

三机定位，适用于在战术地幅内实施直接侦察，或在宽大正面上对重点方向（地域）加强侦察。其定位精度高于双机定位。实施三机定位时，只能在3个两机可定位区域的三层覆盖区域内实施。这一区域称为三机可定位区域。可证明：以A、B为正面配置宽度的A、B、C 3个侦察站，当三机可定位区域的中心恰好是以AB为边的等边三角形的中心时，可以在AB线外侧（面敌方向）获得最大的三机可定位区域的面积和纵深。这一模式为三机定位时侦察站（或测向站）配置的最优模式，如图4所示。

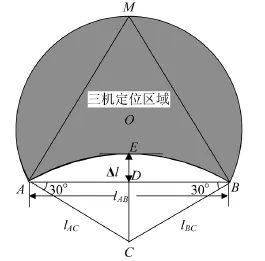
图4　雷达侦察站三机定位有效定位区域

3.2三机定位最优配置的参数计算

在战术地幅内实施雷达侦察时，可依据对空侦察任务要求的定位纵深N，正面宽度P来确定三机定位的相关参数，如图5所示。

设两前沿侦察站A、B距离侦察站C的站距为lAC、lBC，按照最优模式配置时，

可定位区域的最大面积

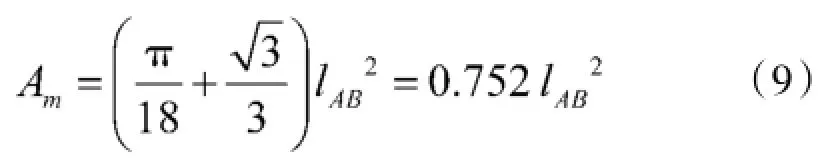
三机可定位区域的实用最大纵深

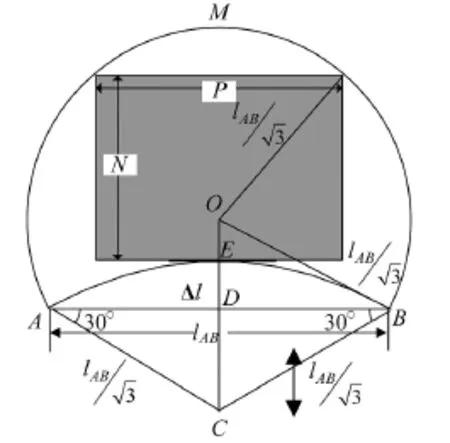
图5　三机定位的定位区域与任务地幅示意图

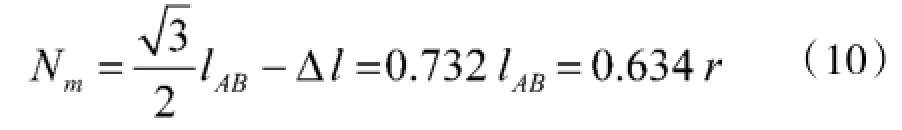
C站到可定位区域边线的距离

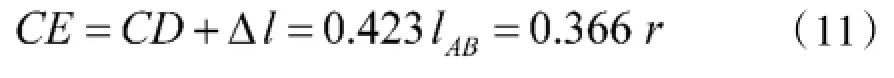
在战术地幅内实施侦察时，A、B两站的站距lAB与作战任务要求的侦察定位纵深N、正面宽度P之间的关系为：

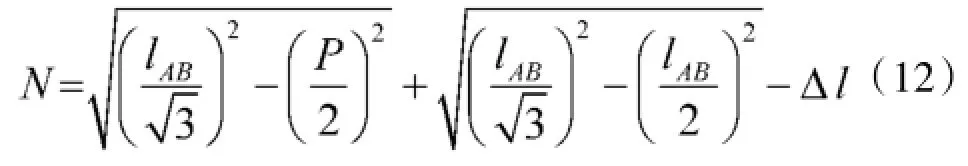
将Δl=0.134lAB代入式（12），解得：又。

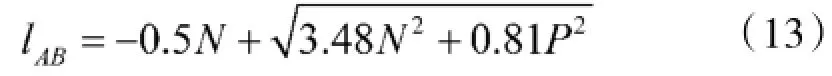
式中：HL为雷达天线应配置的最低高度。

解得：

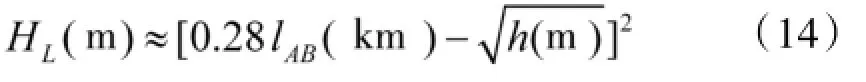
4　实例

按照外军进攻战斗时，集团军正面宽度15 km～30 km，纵深15 km～40 km，取最大战术侦察地幅为：定位纵深N=40 km，正面宽度P=30 km。

由式（13），可计算，我对空侦察雷达阵地两个前沿站A、B的站距

如要求对100 m高度的超低空空袭目标实施定位，则由式（14），对空侦察雷达站阵地最低高度应为

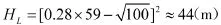
对空侦察两个前沿雷达阵地与战线的距离

5　结论

本文在分析雷达阵地的侦察范围与定位条件基础上，利用几何方法提出双机定位和三机定位的最优配置模式，分别建立双机定位和三机定位的最优站距、定位纵深、配置间隔、阵地高度等相关参数的计算模型，为科学配置对空侦察雷达阵地提供了定量决策依据。实际中，对空侦察雷达阵地的配置还应考虑站点的阵地条件、雷达的适用性、阵地四周地物遮蔽条件等因素。综合考虑多种限制条件的对空侦察雷达阵地优化配置问题有待深入研究。

［1］邵国培.电子对抗作战效能分析［M］.北京：解放军出版社，1998.

［2］（俄罗斯）加加林空军学院.电子战战役战术计算方法［M］胡晓惠，译.北京：空军指挥学院，2002.

［3］闫宗广.电子对抗战术学［M］.北京：解放军出版社，1998.

［4］蔺美青.面向效能优化的无源雷达作战部署方法研究［J］.空军预警学院学报，2013，25（2）：212-214.

［5］王智显.超远距离目标的交叉定位算法研究［J］.现代雷达，2008，30（12）：39-41.

［6］夏大永.三站定位区域计算仿真研究［C］//北京：第九届全国雷达学术年会论文集，2004（8）：709-711.

［7］郁春来.无源定位技术体制及装备的现状与发展趋势［J］.空军雷达学院学报，2012，26（2）：79-85.

［8］程东升.多站无源探测系统实际作战能力综合分析［J］.现代雷达，2009，31（7）：12-16.

Research on Configuration Optimization of Electronic Countermeasure Air Reconnaissance Radar Position

GUO Qiang，GAO Jian-jun，ZHANG Gong-yin
（Air Defense Forces Academy，Zhengzhou 450052，China）

Aimed at the optimization configuration problem of electronic countermeasure air reconnaissance radar position，the paper analyzes the reconnaissance scope and positioning condition at the radar station，proposes the optimal configuration modes of dual-unit positioning and ternary-unit positioning，and respectively sets up the calculation models related to the optimal station spacing，positioning depth，configuration interval，position height and other relevant parameters of dual-unit positioningandternary-unitpositioning.Therealexample'scalculationoftheoptimization configuration problem of electronic countermeasure air reconnaissance radar position indicates that the model is practical and effective.

electronic countermeasure，radar，positioning，configuration，optimization

TN958.97

A

1002-0640（2016）07-0089-03

2015-06-14

2015-07-10

郭强（1981-），男，河南唐河人，硕士研究生，讲师。研究方向：防空武器系统优化论证。