一种改进的量子粒子群算法*

彭　广，方洋旺，张　磊，刁兴华，徐　洋

（空军工程大学航空航天工程学院，西安　710038）

一种改进的量子粒子群算法*

彭广，方洋旺，张磊，刁兴华，徐洋

（空军工程大学航空航天工程学院，西安710038）

量子粒子群算法是将量子计算与粒子群算法相结合的一种新的优化方法。首先利用相位角进行实数编码，将动态量子旋转门引入到粒子群算法中，采用自适应变异，提出了一种改进的量子粒子群算法。然后运用Penalized函数和Ackley函数测试了该算法的性能。最后将该算法应用到武器目标分配模型中，获得了最优的分配方案。仿真研究表明，该算法具有收敛速度快、搜索能力强和稳定性高的特点。

量子粒子群算法，实数编码，动态量子旋转门，自适应变异，武器目标分配

0　引言

为了使多种智能算法优势互补，遵循“组合优化”的思路，对不同智能优化算法进行融合是一个重要的研究思路。量子进化算法（QEA）就是量子计算与进化计算相融合的产物［1］，它将量子比特的概率幅表示方式应用于染色体的编码，使得染色体能够以概率表示所有状态。同时，QEA利用染色体最优个体的信息来更新量子旋转门，使整个种群向当前最优解快速收敛。其中，Narayanan等［2］于1996年首次将量子理论与进化算法相结合，提出了量子衍生遗传算法（QIEA）的概念。Han等［3-5］将其扩展为量子进化算法，实现了组合优化问题的求解。孙俊等［6］将量子算法引入到粒子群算法中，提出了一种量子粒子群算法（QPSO）。方伟等［7］讨论了QPSO的收敛性，证明QPSO是一种全局收敛的算法。文献［8］将协同搜索策略用于QPSO算法中，以解决进化类算法的早熟问题，但通信频率控制参数以及子种群大小不容易确定；文献［9］分别基于势阱、谐振子和方势阱提出了改进的量子势阱粒子群优化算法，通过对比发现势阱的性能更优；文献［10］将遗传算法中的交叉、变异操作引入到QPSO算法中，较好地解决了车辆路径问题，但算法的运行时间较长；文献［11］提出了一种二进制编码的量子粒子群算法，用于解决离散空间优化问题，但在解决高维复杂优化问题时，算法会产生编码“长度灾”和频繁编、解码问题。此外，通过对算法进行改进，QPSO算法已经成功应用于滤波器设计、系统辨识、航路规划以及图像处理等领域［12-15］。虽然量子粒子群算法与粒子群算法相比有更好的全局搜索能力，但仍然容易陷入局部最优，出现早熟的问题，算法稳定性需要进一步提高。

为了进一步改善量子粒子群算法的性能，本文采用组合最优方案，基于文献［16］提出的具有量子行为的实数编码进化算法，拟采用相位角编码的实数编码方式，将动态量子旋转门引入到粒子群算法中，采用自适应变异，提出一种改进的量子粒子群算法。然后运用Penalized函数和Ackley函数测试该算法的性能。最后将该算法应用到武器目标分配模型中，成功获得了最优的分配方案，验证了算法的合理性和有效性。

1　基于相位角编码的量子粒子群算法

考虑n维连续空间目标函数优化问题

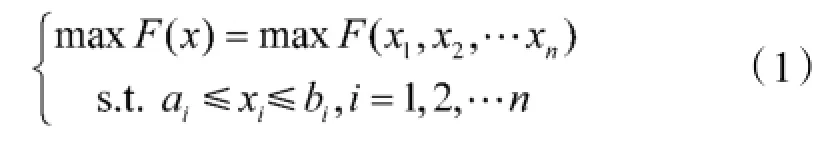
式中，F（x）为目标函数；变量x=（x1，x2，…，xn）∈Rn；ai和bi为第i个变量的上下限。

1.1相位角编码染色体

相位角编码染色体是一种实数编码方式，量子染色体chrom（t）的第i个量子位由变量xi对应的相位角θi表示，长度解由空间的维数n决定，则相位角染色体编码可以描述为：

其中，θi∈［-π/2，π/2］；通过相位角θi的更新，并按照一定的映射关系从相空间映射到解空间，实现染色体的进化搜索。

变量xi和对应相位角θi之间的映射关系可表示如下：

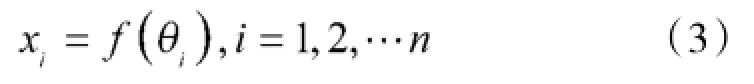
不同的映射关系对算法的性能有着较大的影响，本文选取有较好优化性能的正弦函数作为变量与对应相位角之间的映射关系［17］：

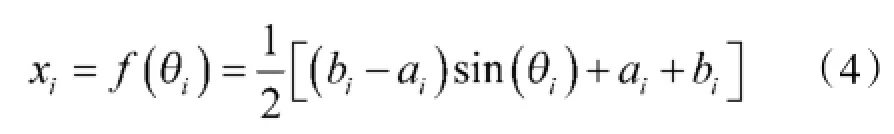
具体关系如图1所示：

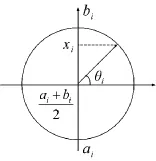
图1　变量和相位角之间的映射关系

在相位角编码染色体中，染色体chrom（t）中的第i个量子位的相位角θi的具体计算方法为：

其中，rand0是［0，1］间均匀分布的随机数。从中可以看出，染色体量子位的相位角θi不再表示一个确定的角度值，而是可以表现为区间［-π/2，π/2］上的所有角度值，同时由于叠加态特性染色体chrom（t）映射到解空间后就能够表达优化问题的所有可行解，丰富了种群的多样性。

1.2量子染色体的速度和位置更新

借鉴基本粒子群算法的基本思想，首先在可行解空间和速度空间初始化粒子群，即确定粒子群的初始位置和初始速度，其中初始位置代表问题的可行解。在本文中，粒子群的初始位置即为相位角编码初始化的量子染色体，初始速度dangle=0。n维搜索空间中的第i个粒子的位置和速度可分别表示为：

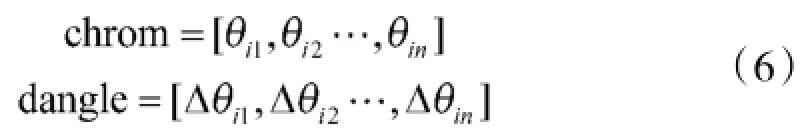
通过评价各粒子的适应度，确定t时刻每个粒子所经过的最佳位置selfchromi=｛φi1，φi2，…，φin｝以及群体中所发现的最佳位置bestchrom，再按如下迭代公式分别更新各粒子的速度和位置

式中，w为惯性因子；c1和c2为正常数，称为认知因子和社会因子；r1和r2为［0，1］间均匀分布的随机数。

1.3动态量子旋转门

在量子理论中，各个量子状态之间的转换主要是通过量子门实现的。而量子染色体进化是量子进化算法的核心，是提高种群适应度的关键手段。在量子粒子群算法中，量子旋转门的实质就是改变量子染色体的相位角。通过动态量子旋转门不断地更新操作，可使种群更快地收敛到最优解。

对于t代种群中的染色体chrom（t），经过动态旋转门旋转，其t+1代染色体chromi（t+1）的第j个量子位的相位角为

其中，Δθij（t）为量子旋转门的旋转角；Δθbj（t）为t代最优解对应的染色体θg（t）的第i个量子位的相位角。

量子门旋转角极大地影响算法的搜索效率和精度，一般而言，初期算法需要较大的旋转角以粗粒度探索未知空间；在后期，随着解的质量的提高，算法需要逐步减小旋转角以细粒度搜索当前空间。为此，本文采用动态旋转角来代替固定旋转角，在算法迭代过程中动态调整旋转角大小。对于染色体chrom（t），其动态旋转角为：

式中，Δθ0为初始旋转角；λ为正常数，用于调整转角的变化率；NCmax为最大迭代次数。

1.4自适应变异

在量子染色体的速度和位置更新及动态量子旋转门的作用下，所有染色体向当前最优染色体快速演化，这样在搜索过程中染色体可能无法覆盖整个解空间。为保持种群多样性，避免算法陷入局部最优，引入了量子染色体自适应变异的思想。染色体chrom（t）经过自适应变异操作后变为：

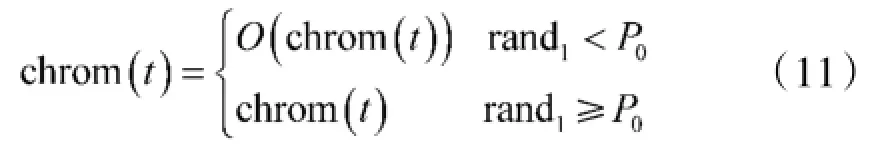
式中，rand1是［0，1］间均匀分布的随机数；P0为0～0.1之间的常数，称为变异概率；O（chrom（t））为相位角重新编码染色体，为新个体的产生提供机会。

2　量子粒子群算法流程

量子粒子群算法具体步骤如下：

Step1：参数初始化。t=0，种群初始化。

Step2：适应度评价。将量子染色体映射到对应解空间，进行第一次适应度评价，粒子历史最优值是粒子本身，种群历史最优值是适应度最大的值。

Step3：速度和位置更新。根据式（7）和式（8）更新量子染色体的速度和位置。

Step4：保留最优个体。将更新后的量子染色体再次映射到对应解空间，分别计算其目标函数值，更新个体极值和群体极值，确定群体最优解并保留。判断是否满足约束条件：是，则程序结束运行；否，转到Step5。

Step5：用动态量子旋转门对染色体进行更新。

图2　量子粒子群算法流程图

Step6：自适应变异，变异概率设置为0.05。

Step7：迭代次数t=t+1，算法转到Step3继续执行。

3　标准测试函数研究

为测试算法的性能，将量子粒子群算法（QEA-PSO）和基本粒子群算法（PSO）及量子进化算法（QEA）分别对两个标准测试函数进行求解。

1）Penalized函数

其中，yi=1+0.25（xi+1），xi∈［-50，50］，全局最小值点为（-1，-1，…，-1），全局最小值为0。

2）Ackley函数

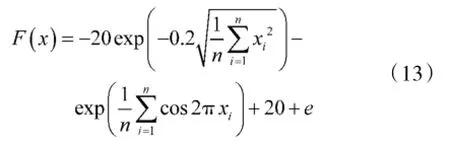
其中，xi∈［-32，32］，全局最小点（0，0，…，0），全局最小值为0。

两个标准测试函数的维数均为n=30，3种算法的种群大小均为m=30，最大迭代次数NCmax=2 000，其他具体参数设置如下：

PSO：惯性因子w=0.729，记忆因子c1=c2=1.494；

QEA：初始旋转角Δθ0=1.1°，调整转角变化率的参数λ=6；

QEA-PSO：惯性因子w=0.729，记忆因子c1=c2= 1.494，初始旋转角Δθ0=1.1°，调整转角变化率的参数λ=6。

每次仿真实验均进行50次仿真，并统计仿真结果的平均值、最优值、最劣值和方差，得到的统计结果如表1和表2所示。

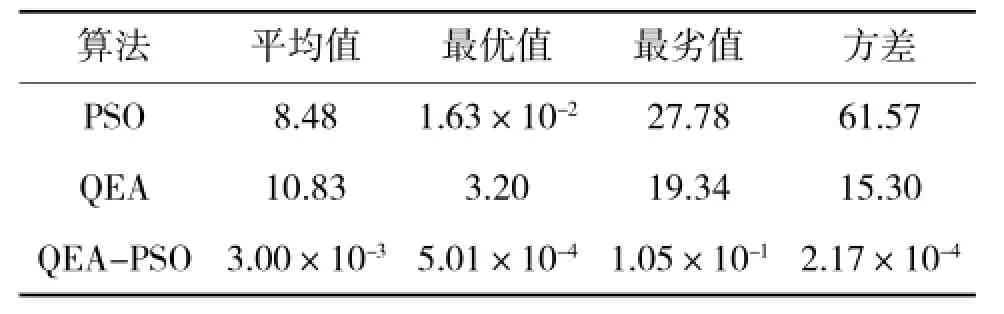
表1　Penalized函数优化结果

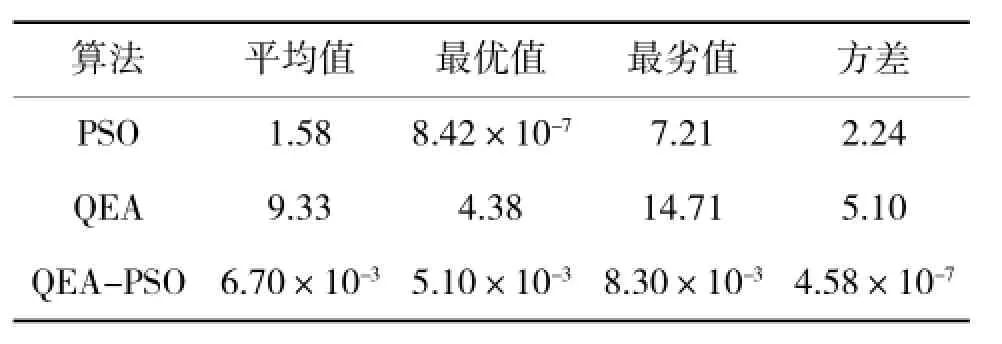
表2　Ackley函数优化结果

仿真结果表明，对于具有较多局部最小值的标准测试函数，PSO虽然有时能搜索到精度较高的最优解，但算法的性能极不稳定，每次寻优结果相差较大；QEA对于具有较多局部最优值的高维函数寻优效果极差；而QEA-PSO无论是寻优精度还是算法的稳定性都优于其他两种算法。

图3和图4分别表示3种算法在50次独立仿真中目标函数值的平均的变化曲线。从对比的收敛曲线可以看出，对于求解复杂的高维函数，QEA-PSO寻优速度快，搜素精度高，算法稳定性好。

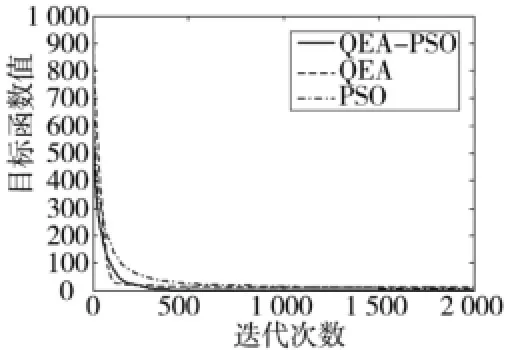
图3　Penalized函数仿真结果

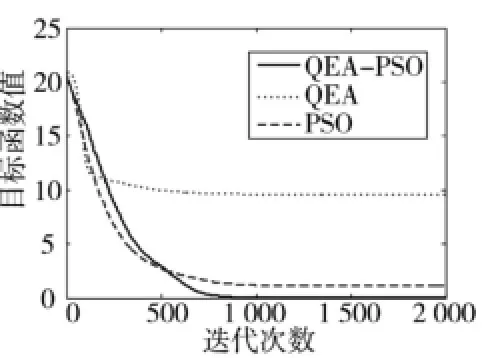
图4　Ackley函数仿真结果

4　实例研究

本文采用文献［18］的武器目标分配模型进行检验，假设我方具有两组不同类型的导弹，对3个目标进行打击。第1组有6枚导弹，第2组由10枚导弹。求最优分配方案，使导弹对目标的毁伤指标最大。

目标函数为：

约束条件：

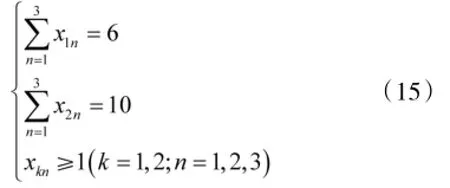
其中，目标的危险程度系数wn和目标易损性pkn如表3所示。

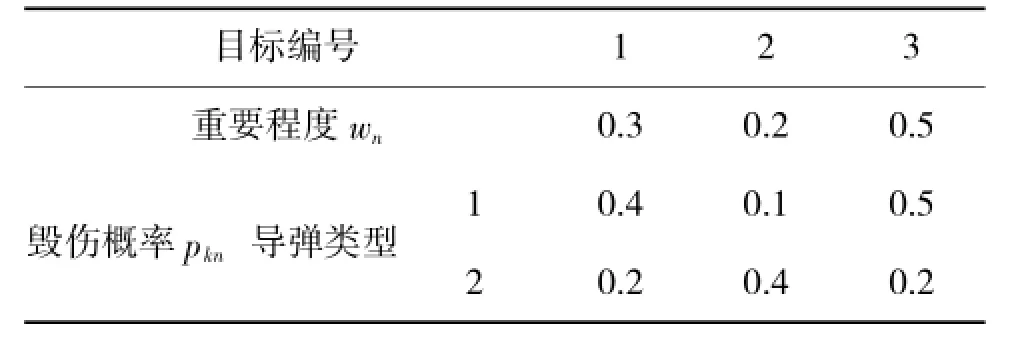
表3　目标重要程度和目标易损性系数

为了验证算法的性能，将量子粒子群算法（QEA-PSO）和基本粒子群算法（PSO）及量子进化算法（QEA）作仿真比较。其中，粒子群种群大小为10，最大迭代次数NCmax=100，其他具体参数设置如下：

PSO：惯性因子w在0.5～0之间线性取值，记忆因子c1=c2=2；

QEA：初始旋转角Δθ0=10°，调整转角变化率的参数λ=25；

QEA-PSO：惯性因子w在0.5～0之间线性取值，记忆因子c1=c2=2，初始旋转角Δθ0=10°，调整转角变化率的参数λ=25。

用上述3种优化算法分别进行仿真实验，得到的染色体适应度变化趋势如图5所示。

图5　适应度变化趋势

目标函数值记录结果如下页表4所示。

针对上述导弹武器火力分配模型，以往的文献中也用不同的方法作出了不同的研究。例如文献［19］用动态规划方法求解的结果为F=0.911 3，显然不是最优解。文献［20］用遗传算法求解，在必须使用先验知识的前提下，可以得到最优解F=0.917 8，但这并不符合实际需要。文献［18］采用改进粒子群算法求解此问题，在迭代6次的时候可以得到最优解F=0.917 8，而QEA-PSO只需要迭代4次，说明QEA-PSO的优化效率更高。

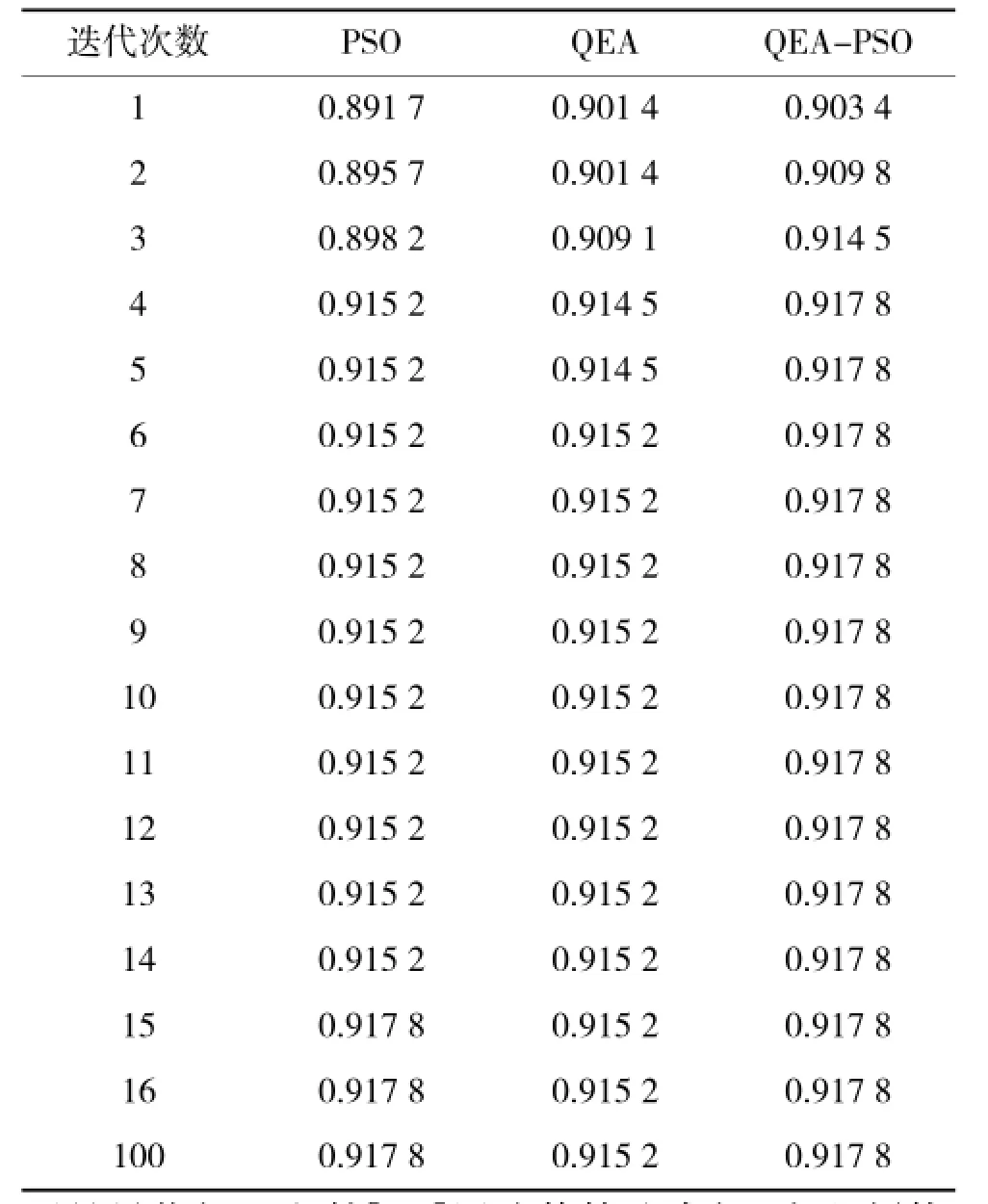
表4　目标函数值记录结果

对比和分析上述仿真结果可以看出，在PSO、QEA、QEA-PSO 3种算法中，QEA的变换过程相对简单，寻优过程容易陷入局部最优从而出现早熟收敛；PSO和QEA相比，PSO全局搜索能力比QEA强，通过一定的迭代次数能找到全局最优解；QEA-PSO结合了QEA和PSO两种算法各自的优点，具有收敛速度快、全局寻优能力强、算法稳定性高等特点。

5　结论

本文提出了一种改进的量子粒子群算法。该算法利用相位角进行实数编码，保证了种群的多样性和进化的方向性，实现了算法局部搜索和全局搜索的平衡。为进一步将该算法应用到路径规划、运筹调度、图像处理以及控制器设计等领域奠定了坚实的理论基础。

［1］王凌.量子进化算法研究现状［J］.控制与决策，2008，23

（12）：1321-1326.

［2］NARAYANAN A，MOORE M.Quantum-inspired genetic algorithm［C］//IEEE Congress on Evolutionary Computation，1996：61-66.

［3］HAN K H，KIM J H.Quantum-inspired evolutionary algorithm for a class of combinatorial optimization［J］.IEEE Trans on evolutionary computation，2002，6（6）：580-593.

［4］HAN K H，KIM J H.Quantum-inspired evolutionary algorithmwithanewterminationcriterion，Hεgateand two-phase scheme［J］.IEEE Trans on Evolutionary Computation，2004，8（2）：156-189.

［5］KIM Y，KIM J H，HAN K H.Quantum-inspired multi objective evolutionary algorithm for multi objective 0/1 knapsack problems［C］//IEEE Congress on Evolutionary Computation，2006：2601-2606.

［6］SUN J，FENG B，XU W B.Particle swarm optimization with particles having quantum behavior［C］//Proceedings of IEEE Congress on Evolutionary Computation，2004：325-331.

［7］方伟，孙俊，谢振平，等.量子粒子群优化算法的收敛性及控制参数研究［J］.物理学报，2010，59（6）：3686-3694.

［8］周頔，孙俊，须文波.具有量子行为的协同粒子群优化算法［J］.控制与决策，2011，26（4）：582-586.

［9］李盼池，王海英，宋考平，等.量子势阱粒子群优化算法的改进研究［J］.物理学报，2012，61（6）：25-34.

［10］黄震.混合量子粒子群算法求解车辆路径问题［J］.计算机工程与应用，2013，49（24）：219-223.

［11］奚茂龙，孙俊，吴勇.一种二进制编码的量子粒子群优化算法［J］.控制与决策，2010，25（1）：99-104.

［12］余静，吴乐南，靳一.基于量子粒子群算法优化的数字冲击滤波器自动设计［J］.东南大学学报，2012，42（2）：224-228.

［13］黄宇，韩璞，刘长良，等.改进量子粒子群算法及其在系统辨识中的应用［J］.中国电机工程学报，2011，31（20）：114-120.

［14］张航，刘梓溪.基于量子行为粒子群优化算法的微型飞行器三维路径规划［J］.中南大学学报（自然科学版）. 2013，44（2），58-62.

［15］关泽群，周敏璐，王建梅.一种改进的隐含相似性光学和SAR图像配准算法［J］.同济大学学报（自然科学版），2013，41（4）：600-606.

［16］张磊.巡航导弹航路规划与跟踪关键技术研究［D］.西安：空军工程大学，2014.

［17］傅阳光.粒子群优化算法的改进及其在航迹规划中的应用研究［D］.武汉：华中科技大学，2011.

［18］杨懿，武昌，刘涵.改进粒子群算法在导弹火力分配中的应用［J］.火力与指挥控制，2007，32（1）：60-63.

［19］解春明，李德胜.地地导弹突击目标火力分配模型分析［J］.军事运筹与系统工程，2004，18（1）：29-32.

［20］冯杰.遗传算法及其在导弹火力分配上的应用［J］.火力与指挥控制，2007，29（2）：43-45.

Research on an Improved Quantum Particle Swarm Optimization Algorithm

PENG Guang，FANG Yang-wang，ZHANG Lei，DIAO Xing-hua，XU Yang
（School of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi'an 710038，China）

Quantum particle swarm optimization algorithm is a new algorithm based on the combination of quantum algorithm and particle swarm optimization algorithm.In this paper，an improved quantum particle swarm optimization algorithm is proposed：first，using the phase angle to encode quantum chromosome；second，the dynamic quantum rotation gate is introduced to particle swarm optimization；third，the adaptive mutation is applied.Furthermore，the performance of the algorithm is tested by Penalized function and Ackley function.Finally，the weapon target assignment model is solved by the improved quantum particle swarm optimization algorithm to obtain the optimal assignment.The simulative results show that the proposed algorithm has the characteristics of rapider convergence，powerful global search capability and better stability.

quantum particle swarm optimization algorithm，real-coded，dynamic quantum rotation gate，adaptivemutation，weapontargetassignment

E911

A

1002-0640（2016）07-0092-05

2015-06-09

2015-07-10
*

中国博士后科学基金资助项目（2014M562630）

彭广（1992-），男，湖北广水人，硕士。研究方向：智能计算，空天武器系统仿真。