一类不确定非线性时滞系统的鲁棒容错控制*

吴文丽，王永成，李桂芳

（1.南京航空航天大学民航学院，南京　211106；2.郑州航空工业管理学院，郑州　450015）

一类不确定非线性时滞系统的鲁棒容错控制*

吴文丽1，王永成2，李桂芳1

（1.南京航空航天大学民航学院，南京211106；2.郑州航空工业管理学院，郑州450015）

针对一类非线性时滞系统，基于Lyapunov稳定性理论，讨论了不确定参数系统的鲁棒容错控制问题。当故障在失效的传感器以及失效的执行器发生时，且非线性不确定性满足一定的增益条件，通过基于线性矩阵不等式（LMI）方法各自给出了故障在传感器和执行器失效发生时，闭环系统渐近稳定的存在条件及相应控制器的设计方法。一个设计算例的仿真结果表明了该方法是有效的。

时滞系统，稳定性，不确定性，容错控制

0　引言

在现实生活中，工程系统一般都在向着大规模的目标发展，故障一旦发生往往会形成资产与人员的巨大损失。为了系统的可靠性被提高，系统的容错能力［1］也必须被考虑。在现实体系中，因为误差建模、不同环境和退化的元器件等影响要素，不确定性是难以避免的，并且有测量器件的不灵敏性和延时传输等因素，时滞也会产生。在实际系统中，不确定性通常具有非线性特征，而这三者的存在，系统性能［2-3］都会被影响。于是，不确定非线性时滞系统鲁棒容错控制课题的研究具备必要的理论意义和工程应用价值。

近年来，不确定非线性时滞系统的容错控制问题已有很多的研究成果［4-6］。文献［4］考虑了不确定系统并带有时滞的鲁棒容错控制问题，基于LMI分别给出了执行器和传感器失效具有完整性的容错控制器的设计方法。文献［5］研究了一类不确定性不满足匹配前提的线性不确定时滞系统，研究具有更普遍意义的执行器连续增益故障模型，给出了容错控制器的方法。文献［6］研究了一类具有非线性特征、干扰输入和时滞特性的鲁棒容错控制问题，给出控制器存在的充分条件和构造性设计方法。但是往往没有同时考虑不确定参数矩阵和非线性特征。

本文考虑了一类同时具有参数不确定性以及时滞的非线性系统传感器和执行器失效的鲁棒容错控制问题，基于LMI方法，在非线性不确定性满足增益条件下闭环系统仍能渐进稳定的状态反馈控制器的存在条件及设计方法。

1　系统描述

考虑下述描述系统：

式（1）中：x（t）∈Rn为状态向量，u（t）∈Rm为控制输入；A，Ad，B为已知具有适当维数的常数矩阵；标量d＞0为延时；φ（t）为连续向量值初始函数；ΔA，ΔAd 和ΔB是不确定参数矩阵，反映了系统模型中的参数不确定性，有如下形式：ΔA（t）=D1F1（t）E1，ΔAd（t）= D2F2（t）E2，ΔB（t）=D3F3（t）E3，式中D1，D2，D3，E1，E2，E3为适当维数的常数矩阵，F1（t），F2（t），F3（t）表示未知的时变实值连续矩阵函数，它的元素Lebesgue是可测的，且

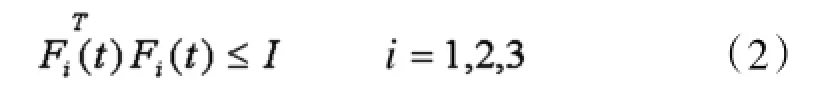
Δf1，Δf2为具有适当维数的非线性连续可微函数向量或矩阵，并满足：

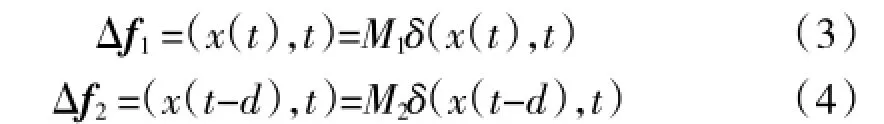
其中，M1，M2为已知定常矩阵，δ为未知的n维非线性连续可微函数向量，且满足：

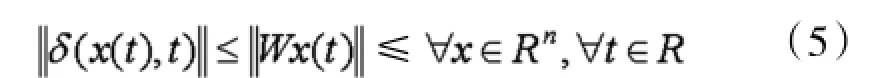
式（5）中，W∈Rn×n为加权矩阵，表示Euclidean范数。由式（5）可知，

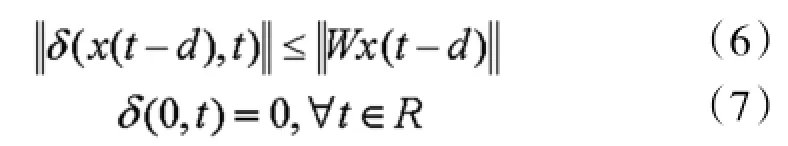
则x（t）=0.是自由系统的平衡点。

假设（A，B）可控，应用状态反馈控制器，即

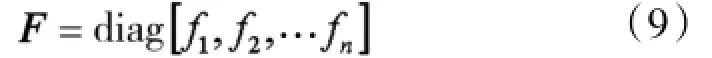
存在传感器故障时闭环系统为

如果执行器可能失效，引入开关阵L，则

则存在执行器故障时闭环系统为

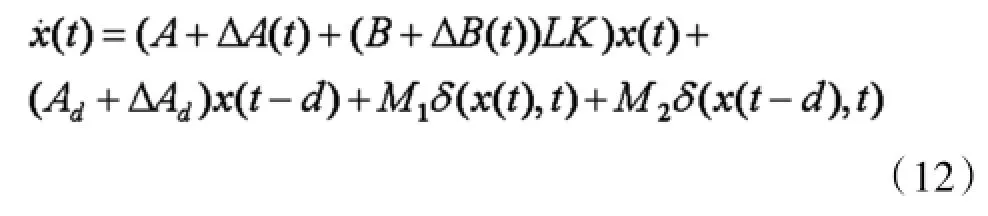
本文的设计要求是：寻求状态反馈控制器式（8），使得存在传感器故障时闭环系统式（10）或者存在执行器故障时闭环系统式（12）是渐进稳定的。

2　主要结果

引理1对于任意适当维数矩阵X，Y和实数α＞0有

引理2A，D，E和F为适当维数的实矩阵，若FTF≤I，则称任意对称矩阵P及标量ε＞0，如果有P-εDDT＞0,则（A+DFE）TP-1（A+DFE）≤AT（P-εDDT）-1A+ε-1ETE（14）

定理1如果存在适当维数的正定对称矩阵P＞0，以及正标量ε1，ε2，ε3，ε4，ε5，α1，α2，λ以及γ，满足如下的LMI：

则当传感器失效时，闭环系统式（10）是渐进稳定的，且状态反馈增益阵为

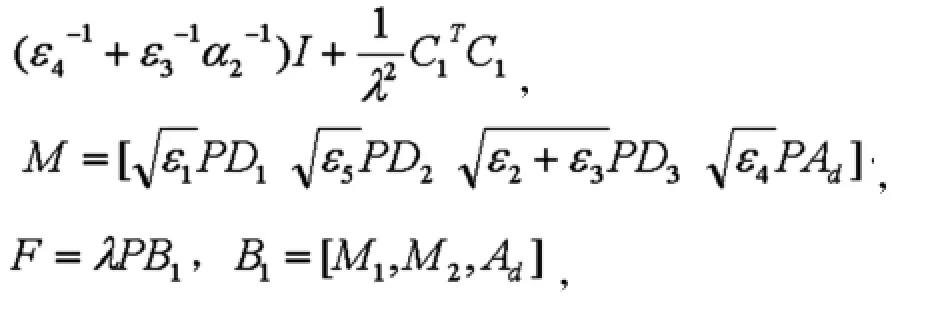
证明为方便简记，记x=x（t），xd=x（t-d），δ=δ（x（t），t），δd=δd（x（t-d），t）。令φ（t，x）为自由系统（10）在初始条件x（t）=φ（t）下的解。对任意Δf1，Δf2满足式（6）的系统式（10），取Lyapunov函数：

其中，P，Q为正定对称矩阵，且V（x，t）沿方程式（10）的导数如下：

取反馈增益K=-γ-1BTP，根据引理1和引理2，得

根据引理3的Schur定理，上述不等式等价于式（15）。如果满足式（15），则：

令Q=WTW+I＞0，则

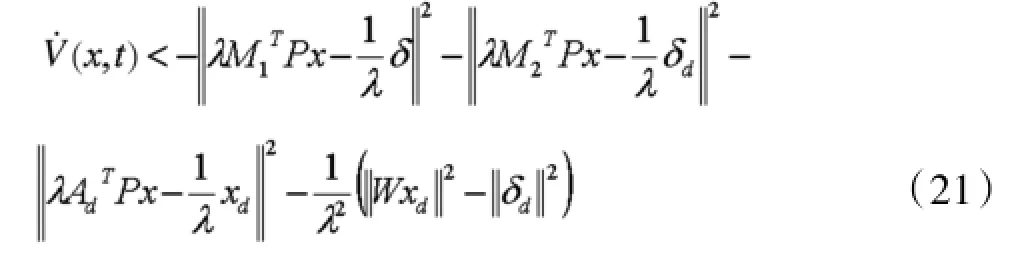
由Lyapunov稳定性理论，传感器失效下的闭环系统仍然是渐进稳定的，定理1得证。

定理2如果存在适当维数的正定对称矩阵P＞0和正标量ε1，ε2，ε3，ε4，α1以及γ，满足以下的LMI：

则当执行器失效时，闭环系统式（12）仍渐进稳定，且反馈增益阵为

证明与定理1的证明相似，在此省略。

3　设计实例

根据定理1可知，控制器u（t）是系统式（1）的一个在失效的传感器发生故障时具有完整性的容错控制器。下页图1和图2是初始系统条件为x（t）=［150 1］T时的仿真结果。图1为正常时时滞系统的零输入响应，图2为第1个传感器发生故障时的零输入响应。仿真结果表明本文提出的方法是有效的。

图1　正常时滞系统的零输入响应

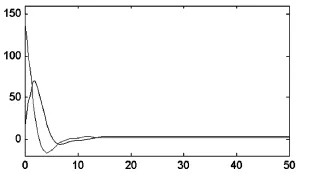
图2　第1个传感器发生故障时的零输入响应

4　结论

本文针对一类同时具有参数不确定性以及时滞的非线性系统传感器和执行器可能失效的情况下，基于Lyapunov稳定性理论，基于LMI方法，提出了确保闭环系统在其失效产生故障时仍能渐进稳定的容错控制器的满意方法，这个方法用设计实例及仿真结果表明是有效的。

［1］孙金生，李军，王执铨.时滞不确定系统的鲁棒容错控制［J］.控制理论与应用，1998，15（2）：267-271.

［2］WANG，Z，D，HUANG，B，UNBEHAUEN H.Robust reliable control for a class of uncertain nonlinear state-delayed Systems［J］.Automatica，1999，35（5）：955-963.

［3］QU Z H，CURTIS M I.Robust control of a class of nonlinear uncertain systems fault tolerant against sensor failures and subsequent self-recovery［C］//Proc of the 40th IEEE Conf on Decision and Control.Oriando，2001：1472-1478.

［4］杨虹，孙金生，王执铨，等.时滞不确定系统的鲁棒容错控制［J］.南京理工大学学报（自然科学版），2005，29（2）：132-135.

［5］郑再东，崔宝同.一类不确定时滞系统的鲁棒容错控制［J］.科学技术与工程，2011，11（9）：1999-2002，2011.

［6］张刚，王执铨.不确定时滞系统相容指标下的鲁棒容错控制器设计［J］.控制与决策，2006，（6）：666-671.

［7］俞立.鲁棒控制-线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002：158-212.

Robust Fault-tolerant Control for a Class of Uncertain Nonlinear Time-delay Systems

WU Wen-li，WANG Yong-cheng，LI Gui-fang
（1.School of Civil Aviation，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China；2.Management Colleges of Aircraft Industry of Zhengzhou，Zhengzhou 450015，China）

For a class of nonlinear time-lag systems，which is based on Lyapunov stability theory，the problem of？robust fault-tolerant control for uncertain parameter systems is discussed.When the failure occurs in failed sensor and actuator，the nonlinear uncertainties satisfy certain gain conditions，and based on that linear matrix inequality（LMI）approach gives the existence condition of asymptotic stability of closed-loop system and the design method of corresponding controller when the breakdown caused by the occurrence of two kinds of failure，the simulation results of a design example show that the method is effective.

time-lag systems，stability，uncertain，fault-tolerant control

TP273

A

1002-0640（2016）07-0039-04

2015-06-12

2015-07-10

国家自然科学基金资助项目（61304020）

吴文丽（1989-），女，安徽铜陵人，硕士研究生。研究方向：飞行安全控制，非线性系统控制。