基于纯方位理论的运动舰船长度测量方法*
任继昌,杨晓东,孙少杰,王 旺
(海军潜艇学院,山东 青岛 266042)
基于纯方位理论的运动舰船长度测量方法*
任继昌,杨晓东,孙少杰,王旺
(海军潜艇学院,山东青岛266042)
获得运动舰船的船体长度对于航海避碰和目标识别具有重要的参考价值。然而,由于诸多因素的限制,现有视觉技术难以精确测量。为此,引入了纯方位目标运动分析理论结合双目视觉技术实现对运动舰船长度的测量。首先就所研究问题建立运动模型,推导了基于目标舰船方位、距离参数的舰船长度测量方法,针对该方法测量误差大的问题提出了基于航向、距离、方位的舰船长度测量方法。目标航向无法直接获取,为此引入基于纯方位理论的目标航向视觉估计方法,并进行了仿真验证。最后对两种舰船长度测量模型的误差进行了仿真比较分析,结果表明采用本文提出的“距离航向”法,当观测点位于目标舰船正横左右范围内时误差可以控制在10%内,“方位距离”法误差更小,适用的舷角范围更大。
视觉测量,纯方位理论,航向估计
0 引言
双目立体视觉三维测量技术作为一种非接触测量技术,具有测量速度快、测量精度高、实时性强的显著优点,已被广泛应用于工艺制造、医学、航天、交通、军事等领域[1-5]。通过该技术可以在非接触的条件下对目标进行三维测量,获取其较为精确的三维尺寸数据。然而由于摄像机CCD精密程度、测量系统结构限制,目前为止还未发现通过双目立体视觉对远距离目标进行三维测量的研究。其原因为随着目标距离的增加目标点距离测量误差不断加大,通过几何关系“边角边”所计算得到的舰船长度误差可能接近或超过船体长度。鉴于此原因,本文提出了一种基于航向、方位和距离3个参数测量舰船长度的方法,该方法减少误差较大“边”的使用,增加容易准确测量的“角”的使用,减小了测量误差。舰船的方位角、距离等参数采用计算机视觉的相关技术可以获得,而航向无法直接获取,为此本文引入纯方位理论[6-9]予以实现。
1 测量模型及误差分析

图1 舰船长度测量示意图
为测量以航向θ匀速航行的舰船长度L,采用两个摄像机同时观测目标舰船。图1中,建立平行的双目立体观测结构,左右摄像机的焦距均为f,各自光心用Ol、Or表示,光心之间的距离为B,左摄像机观测到的船首、船尾方位角分别为α1、α2,距离分别为a、b。
1.1双目视觉测距基本原理
图1中,船尾某特征点A在左右摄像机上成像平面上得到的投影点分别为A'、A"的投影得到在各自图像坐标系下的坐标为x1、xr。根据双目立体视觉测量原理可得

其中D=x1-xr表示视差。
由yc可得

同理也可计算距离b。
1.2基于方位和距离的舰船长度测量模型
图1中,获知船首尾距观测点的距离及方位信息后,根据几何原理“边角边”可以求得舰船长度的计算公式:L1

设各测量值a,b,α2,α1的标准差分别为s(a),s(b),s(α2),s(α1),根据误差传递公式,合成测量值的总的标准差为
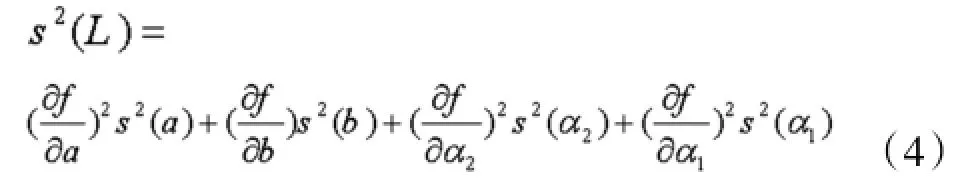
其中:
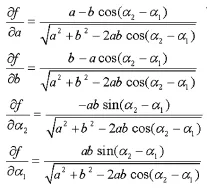
1.3基于航向距离方位的舰船长度测量模型
式(3)给出了一种计算舰船长度的简单方法,只需获得目标舰船首尾的方位和距离即可计算舰船的长度。然而,由于目前的摄像机CCD的精度有限、测量系统结构不能做的很大等因素的限制,双目视觉测距的误差较大,采用式(3)得到的长度误差有可能接近船体长度。鉴于此原因,本文提出采用航向、距离、方位3个参数计算船体长度的方法,该方法减少一条“边”的使用,增加容易准确测量的“角”的使用。
图1中由正弦定理有
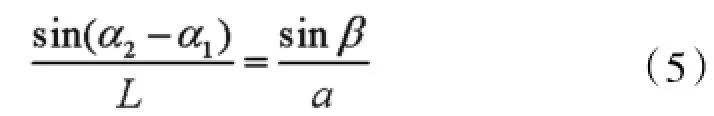
由此可得舰船长度为

其中
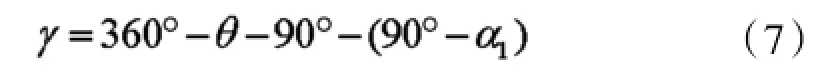
代入式(6)并整理得
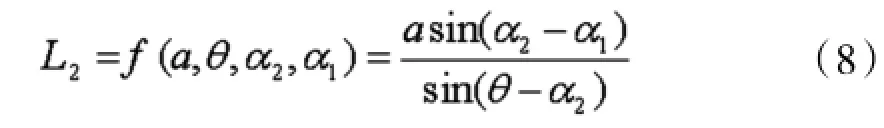
同样设各测量值a,θ,α2,α1的标准差分别为s (a),s(θ),s(α2),s(α1),根据误差传递公式,合成测量值的总的标准差为

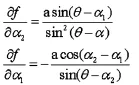
(注:本文仅作理论研究未考虑风流对于舰船姿态的影响,认为舰船中轴线与航向一致。)
为后文讨论方便,这里称式(3)、式(8)的方法分别为“方位距离”法和“距离航向”法。由式(2)、式(3)、式(8)可以看出,要测量舰船长度除已知的B,f外,其余参数均无法直接获取,其中x1、xγ可以采取图像处理技术获取,容易实现。这里重点介绍一下方位α2、α1和航向θ的测量方法,下面逐一给出。
2 目标方位视觉测量
2.1摄像机坐标系、图像坐标系介绍
建立以针孔成像模型为基础的摄像机坐标系(Oc-xcyczc)如图2所示,其中,Oc代表光心位置,zc轴与摄像机光轴重合,P(xc,yc,zc)为空间三维点P坐标,P(xi,yi)为物点像平面坐标。

图2 摄像机坐标系
图像坐标系是存储在计算机中的数字图像的坐标系,其表示方法有两种:第1种以像素单位表示,坐标系原点位于图像的左上角,以(u,v)表示图像中的某一坐标。第2种是用物理单位表示,一般用毫米(mm),设坐标的原点位于(u0,v0)像素点,即主点(摄像机光轴与图像平面的交点)。两种坐标表示方法比较见图3。
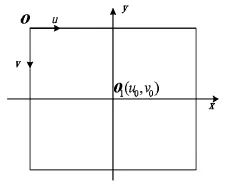
图3 图像坐标系
则图像中任意一个像素在两个坐标系下的坐标有如下关系:

本文采用第2种图像坐标系进行测量。
2.2目标方位测量方法
为测量目标方位以及后文将要介绍的目标航向,需要选取目标上的某个特征点,并实现稳定跟踪。经过比较,采用稳健的Harris角点检测算法[10]进行图像特征点的检测。获取目标特征点的角点坐标值后,进一步采用亚像素特征提取技术优化计算结果[11],最终可获得目标特征点的亚像素级坐标值。
图2中,根据针孔成像原理,光线通过镜头光心将不会产生折射,将通过光心且垂直于镜头的虚拟光线称为主光轴,以主光轴作为目标方位角测量的基准,镜头成像平面上每个像点可看作是不同角度入射光线与像平面的交点,在获取CCD平面图像中的目标像点精确位置以及镜头焦距参数后,结合视觉透视投影关系可推算出目标相对于摄像机的方位信息。定义主光轴与目标在xcOczc平面的投影OcPxz形成的夹角α为目标的方位角

采用上文的角点检测技术可以得到目标像点的像素坐标,根据几何关系,最终可求解得到目标方位
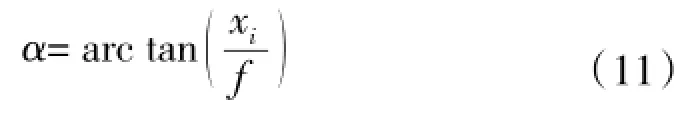
3 基于单站纯方位的目标航向估计
3.1模型分析
为测定目标航向,建立如图4所示目标运动示意图。假定图中目标做匀速直线运动,考虑其在运动平面的二维情形,建立xoy坐标系,x轴指向正东,y轴指向正北,静止观测站(这里指摄像机)位于坐标系原点,目标在xoy平面内以速度v作匀速直线运动,其状态向量为

式中,x0、y0为目标的初始位置,vx、vy为目标沿x轴和y轴方向的速度分量。当状态参数(x0,y0,vx,vy)已知时,目标运动轨迹可唯一确定。
下页图4中,d0为目标初始距离,θ为目标运动航向(以顺时针方向为正),αk为tk时刻时观测到的目标方位角。根据几何关系,可得到观测方位与目标状态向量之间存在如下非线性关系
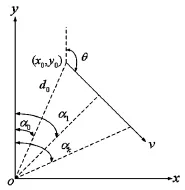
图4 目标运动示意图
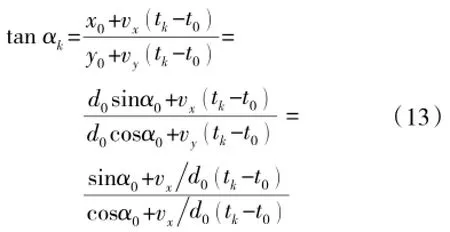
当αj(j=0,1,…,k)也即目标方位序列为已知量,利用上式便可得到关于(vx,vy,d0)的非线性方程组。解出上述3个参数后,即可确定目标运动轨迹,从而实现对目标的定位。此时称系统是完全可观测的。
3.2纯方位目标航向估计
对纯方位目标运动分析的大量研究表明,利用静止单站法所测量的目标方位信息,无法同时解算出目标的航向、距离及速度等全部参数,即由于存在“距离模糊”,系统是不完全可观测的[12]。然而,部分参数是可估计的,下面作进一步分析。
对式(13)进行拟线性化(Pseudo-Linear)处理,当j=1,2,…,k,k≥2时可得到如下方程
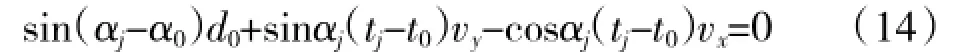
取前k个单位时刻,写成矩阵形式为
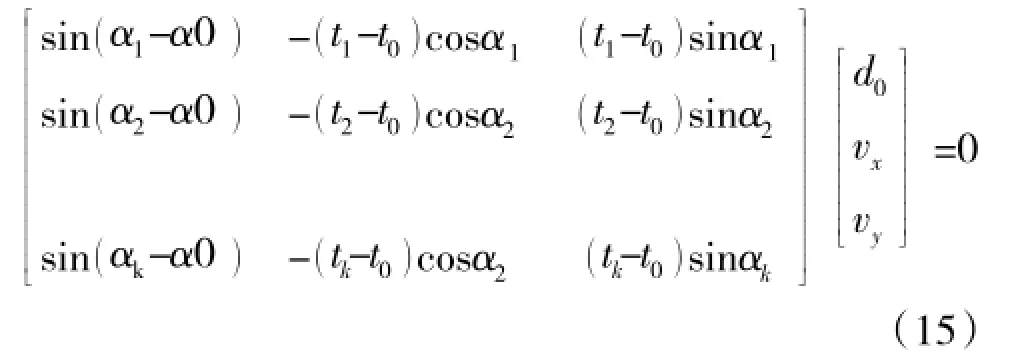
记式(15)左侧系数阵第1列为A1,第2列和第3列为A2,展开可得
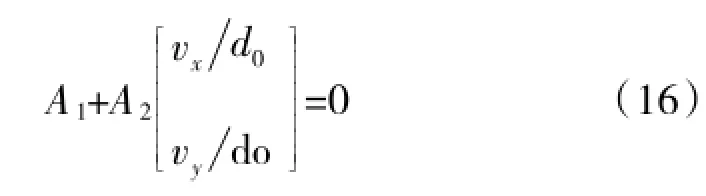
定义X0=[vx/d0vy/d0]T,则式(16)又可写成

对非线性观测方程进行适当的拟线性处理后参考文献[13]中的方法,采用最小二乘法进行估计,最终求解得

其中,
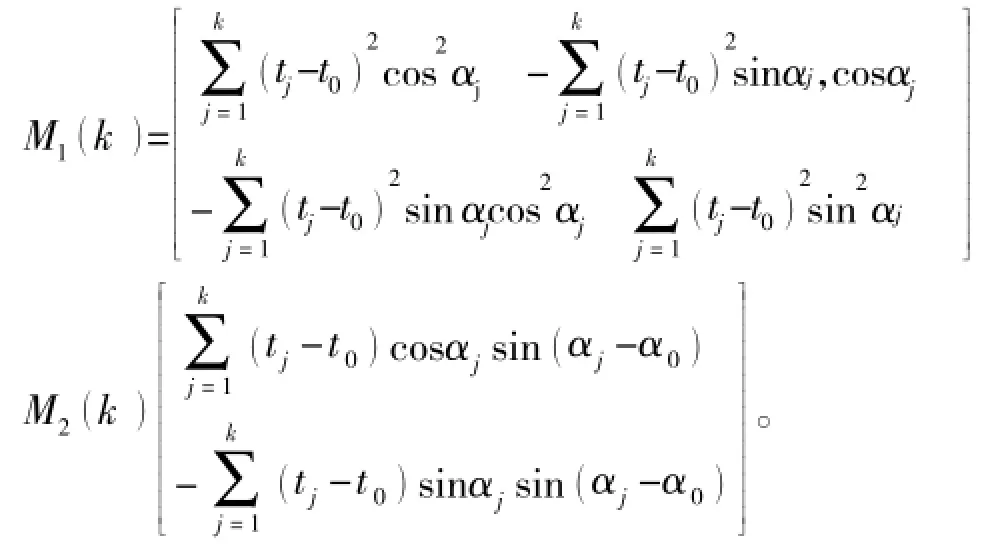
在利用式(18)解出的情况下,可以根据这些信息估计目标航向参数
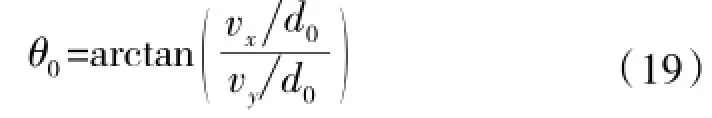
式中θ0需根据正负号判断所在象限,如当且时。

4 仿真验证与分析
4.1基于纯方位法的航向估计
为比较两种舰船长度测量方法的误差大小,首先仿真验证采用纯方位理论获得目标航向的可行性。
设静止观测站位置(0,0)(m),目标于观测站正北以固定航向作匀速直线运动,方位角观测噪声为服从N(0,0.0012)(rad)的高斯白噪声,测量周期T=1s。为研究不同初始条件(目标速度、运动航向、初始距离)对估计算法的影响,分别从以下3种目标运动态势进行分析。
目标运动态势1:目标航向角45°初始距离1000 m,分别以速度10 kn、30 kn航行;
目标运动态势2:目标速度10 kn初始距离1 000 m,分别以航向45°、135°航行;
目标运动态势3:目标初始距离分别为1 000 m、3 000 m,以航向45°、速度10 kn航行。
3种运动态势下目标航向估计效果分别如图5~图7所示,为便于观看,航向估计误差取绝对值。
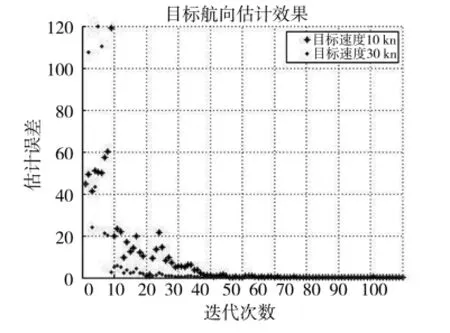
图5 不同速度时目标航向估计性能

图6 不同航向时目标航向估计性能

图7 不同初距时目标航向估计性能
从各图中可以看到,受不同初始条件影响收敛速度有快有慢,但经过不到100次迭代,目标航向估计均能够较好收敛。仿真研究表明,在目标运动速度和初始航向相同的情况下,对于更近距离的目标,利用纯方位方法可以获得相对更高精度的航向估计,目标距离对航向估计精度的影响是很明显的,这很容易理解,因为距离越大,单位时间内目标方位变化越小,导致方位观测站测量误差加大。
4.2船体长度测量模型误差仿真分析
为验证两种测量模型的误差,设置初始条件如下:目标舰船位于观测点正北方向2 000 m处,船体长度L=100 m,各测量值的标准差分别为:
s(α1)=s(α2)=0.002 rad=0.114 6°
s(a)=s(b)=50 m
s(θ)=0.004 rad=0.229 2°
让目标舰船在正北方向分别以航向180°∶0°运动,即舷角φ以0°∶180°变化,测量目标舰船长度在两种模型下的误差,仿真结果如图8所示。

图8 测量误差随舷角变化仿真
从仿真结果可以看出,“方位距离”法的误差曲线呈V字形,而“距离航向”法的误差曲线呈U字形。从两者的误差曲线可以很容易分析出,测量误差的大小随目标舰船的舷角变化而变化,舷角为90°时达到最小值,两条曲线以舷角φ=90°为中心左右对称。其中,“方位距离”法的误差曲线随舷角几乎呈线性下降,当观测点位于目标正横左右约5°以内时误差才降到10%内。而“距离航向”法的误差曲线刚开始随舷角迅速较小,而后在很大一段范围内保持较小值,当观测点位于目标舰船正横左右55°范围内时误差可以控制在即10%内。显然采用“距离航向”测量舰船长度比“方位距离”法误差更小,且误差更稳定。
5 结论
本文提出的基于纯方位理论与双目视觉结合的舰船长度测量方法,相比单纯的基于双目视觉的长度测量方法误差更小,适用的舷角变化范围更大。该方法仅依赖非接触视觉技术即可实现对运动舰船长度测量,这对于航海避碰、目标识别都具有重要意义。同时该方法也可用于其他匀速直线运动目标的非接触测量,在隐蔽军事应用上具有一定参考价值。
[1]全燕鸣,黎淑梅,麦青群.基于双目视觉的工件尺寸在机三维测量[J].光学精密工程,2013,21(4):1054-1060.
[2]武雪梅,刘奇.基于立体视觉的手术导航光学定位系统[J].[3]张庆君,胡修林,叶斌,等.基于双目视觉的航天器间相对位置和姿态的测量方法[J].宇航学报,2008,29(1):156-120.
中国组织工程研究与临床康复,2011,15(35):1712-1715.
[4]岳亮.一种基于双目视觉的安全车距测量方法[J].电视技术,2013,37(15):194-197.
[5]解洪文,王宏伦.基于双目视觉的自动空中加油近距导航方法[J].北京航空航天大学学报,2011,37(2):76-78.
[6]TAEK L S.Observability of target tracking with range-only measurements[J].IEEE Journal of Oceanic Engineerign,1999,23(3):383-387.
[7]DOGANCAY K.Bias compensation for the bearings-only pseudo linear target track estimator[J].IEEE Transactions on Signal Processing,2006,54(1):59-68.
[8]BISHOP A,ANDERSON B,FIDAN B,et al.Bearing-only localization using geometrically constrained optimization[J]. IEEE Transactions on Aerospace and Electronic Systems,2009,45(1):308-320.
[9]石章松,刘忠.单站纯方位目标跟踪系统可观测性分析[J].火力与指挥控制,2007,32(2):26-29.
[10]HARRIS C,STEPHENS M.A combined corner and edge detector[C]//Proceedingsofthe4thAlveyVison Conference.Manchester:Organizing Committee AVC,1988:147-151.
[11]LUCCHESE L,MITRA S K.Using saddle points for subpixel featuredetectionincameracalibrationtargets[C]// Proceeding of the 2002 Asia Pacific Conference on Circuits and Systems,2002:191-195.
[12]孙仲康,周一宇,何黎星.单基地有源无源定位技术[M].北京:国防工业出版社,1996.
[13]刘健,刘忠.纯方位目标运动分析的无偏最小二乘估计算法研究[J].武汉理工大学学报(交通科学与工程版),2010,34(2):262-265.
Research in Length Measurement for Moving Ship Based on Bearing-only Theory
REN Ji-chang,YANG Xiao-dong,SUN Shao-jie,WANG Wang
(Navy Submarine Academy,Qingdao 266042,China)
Getting the length of moving ship has important reference value for collision avoidance and target recognition.However,due to the restrictions of many factors,it is hard to be accurately measured by existing vision technology.Therefore,this article introduces bearing-only theory combined with binocular vision technology to measure the length of moving ship.It first establishes the mathematic model for the studying issue,deduces the length measurement method based on bearing and distance of ship.The above method may lead to a big error,in view of this shortcoming,it proposes a length measurement method based on course,distance and bearing.It is hard to get the target's course,so it introduces the bearing-only theory for estimating the course,and stimulates it.In the end,it analyzes the error of the method by stimulation.Results show that when the observer is located in the ship beam around 55 degrees,the measurement error can be controlled in 10%by the of distancecourse method proposed in this paper;and the measurement error is smaller,angle range is bigger than ‘bearing-distance'method.
vision measurement,bearing-only theory,course estimation
E911
A
1002-0640(2016)07-0023-05
2015-06-15
2015-07-12
海军“十二五”预先研究基金资助项目(401010301030-05)
任继昌(1988-),男,四川盐亭人,博士研究生。研究方向:潜艇导航技术。

