岩石巴西劈裂强度与裂纹扩展颗粒尺寸效应研究

黄彦华，杨圣奇， 2，鞠杨，周小平，赵坚， 4

（1. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州，221116；2. 中国矿业大学 力学与建筑工程学院，江苏 徐州，221116；3. 重庆大学 土木工程学院，重庆，400045；4. 莫纳什大学 土木工程系，墨尔本，VIC 3800）

岩石巴西劈裂强度与裂纹扩展颗粒尺寸效应研究

黄彦华1，杨圣奇1， 2，鞠杨1，周小平3，赵坚1， 4

（1. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州，221116；2. 中国矿业大学 力学与建筑工程学院，江苏 徐州，221116；
3. 重庆大学 土木工程学院，重庆，400045；
4. 莫纳什大学 土木工程系，墨尔本，VIC 3800）

基于一组经室内巴西试验结果标定的类岩石材料细观参数，通过颗粒流程序（PFC）建立圆盘试样离散元模型，对含不同颗粒粒度中心直切槽圆盘试样进行巴西劈裂模拟，分析颗粒尺寸对荷载-位移曲线、拉伸强度和破裂模式的影响，揭示裂纹扩展过程中细观力场、微裂纹以及能量演化规律。研究结果表明：切槽圆盘试样荷载-位移曲线可分为单峰值（type I）、峰值之后软化（type II）以及峰值之后强化（type III） 3种；切槽圆盘试样拉伸强度显著比完整圆盘的低，降幅与切槽倾角和颗粒半径相关；当切槽倾角不变时，拉伸强度总体上随着颗粒半径的增大而增大；而当颗粒半径不变时，拉伸强度随着切槽倾角的增大而减小；当切槽倾角相同时，不同颗粒半径中心直切槽圆盘试样破裂模式显著不同，颗粒尺寸主要影响中心直切槽圆盘试样次生裂纹的萌生和扩展；边界对试样作的功首先用于克服颗粒间黏结以产生裂纹，裂纹在应变能的作用不断扩展，在裂纹产生之后，摩擦能才开始起作用；颗粒的运动程度很低，因此动能很小；边界能与抗拉强度总体上呈正比关系，即边界能越大，拉伸强度越大。关键词：岩石力学；巴西试验；中心直切槽圆盘；颗粒尺寸效应；颗粒流

岩石的力学行为会随着岩样尺寸的不同而改变，即岩石具有显著的尺寸效应。岩石尺寸效应在实际工程中具有重要地位，研究者对尺寸效应进行了大量研究，如：杨圣奇等［1］进行了相同直径、不同长度的（长径比为 0.6～3.0）大理岩试样单轴压缩试验研究；POULSE等［2］进行了不同尺度（相同高径比）煤样单轴和三轴压缩试验与模拟研究；ZHANG等［3］进行了不同尺度（同高径比）岩石材料单轴压缩三维数值模拟；AYATOLLAHI等［4］进行了不同直径中心直切槽圆盘试样巴西试验。然而，这些研究多集中在岩样宏观尺寸对岩石力学特性的影响。岩石作为一种非连续和非均质颗粒材料，不同的岩石材料具有不同的颗粒尺寸分布。WONG等［5-7］在进行大理岩和石膏材料压缩试验研究中，观察到不同的裂纹扩展过程，认为这与大理岩和石膏材料具有不同的颗粒尺寸相关，并由此进行了不同颗粒尺寸分布单裂隙岩石材料力学特性和裂纹扩展单轴压缩数值模拟，指出裂纹起裂应力随着颗粒粒度的减小而减小，而单轴压缩强度与颗粒粒度无明显关系。DING等［8］基于三维离散元模型，进行了多组不同模型尺寸单轴压缩模拟，重点分析了单轴压缩强度、弹性模量和泊松比的变化规律。许尚杰等［9］采用二维离散元方法分析了颗粒粒度对岩石材料应力-应变曲线、裂纹扩展和能量特征的影响规律，认为大颗粒有增强特性和阻止裂纹扩展的作用。KOYAMA等［10］对二维离散元模型中不同颗粒比（dmax/dmin=1.5，2.0和3.0）进行压缩模拟研究。YANG等［11］通过二维离散元模拟研究认为弹性模量、泊松比受颗粒尺寸影响显著，而在L/d（L为模型试样最短边长，d为颗粒平均直径）由5.0增大到62.5时，单轴压缩强度基本无变化。FAKHIMI等［12-13］在二维离散元模拟中发现固定试样尺寸而改变颗粒粒度对单轴压缩强度无明显影响，但拉伸强度随着颗粒半径减小而减小。上述研究表明，颗粒尺寸对拉伸强度的影响远大于对压缩强度的影响，因此，有必要进一步分析拉伸作用下颗粒尺寸效应，以明确颗粒尺寸对拉伸强度及裂纹扩展的影响规律。对颗粒尺寸效应的研究除了进行相应室内试验外，数值模拟也是一种可行的方法。由 CUNDALL等［14］在离散元理论基础上提出的颗粒流法（PFC），在处理岩土材料方面具有连续介质方法不具备的显著优点以及在细观力学方面的独到优势，已被广泛应用于岩石力学与工程方面的研究［15-18］。因此，本文作者采用颗粒流程序建立中心直切槽圆（central straight notched Brazilian disc， CSNBD）盘试样巴西试验模型，分析颗粒粒度对拉伸强度的影响以及裂纹扩展过程中细观力场、微裂纹以及能量的演化规律。

1　数值模型的构建

1.1细观参数验证

细观参数标定选用的是室内类岩石材料圆盘试样巴西试验结果，详细标定过程见文献［19］。PFC模拟采用位移加载，加载速率为0.05 m/s。在PFC中时步若设为4.2×10-8s/步，则0.05 m/s可换算为2.1×10-9m/步，加载板移动1 mm需要约476 190步，因此，0.05 m/s的速率足够低，模拟停止条件设定为加载至峰后20%。

表1所示为所选用的细观参数［20］。由表1所示细观参数模拟获得的拉伸强度为3.37 MPa，而实验拉伸强度为3.38 MPa，相对偏差为0.30%；PFC模拟的应力-应变曲线近似线性段平均斜率为0.642 GPa，而试验曲线平均斜率为0.663 GPa，相对偏差为3.22%。由此可见，PFC模拟获得的力学参数与室内结果非常接近。其中，相对偏差为模拟值与试验值之差的绝对值与两者平均值的百分比。

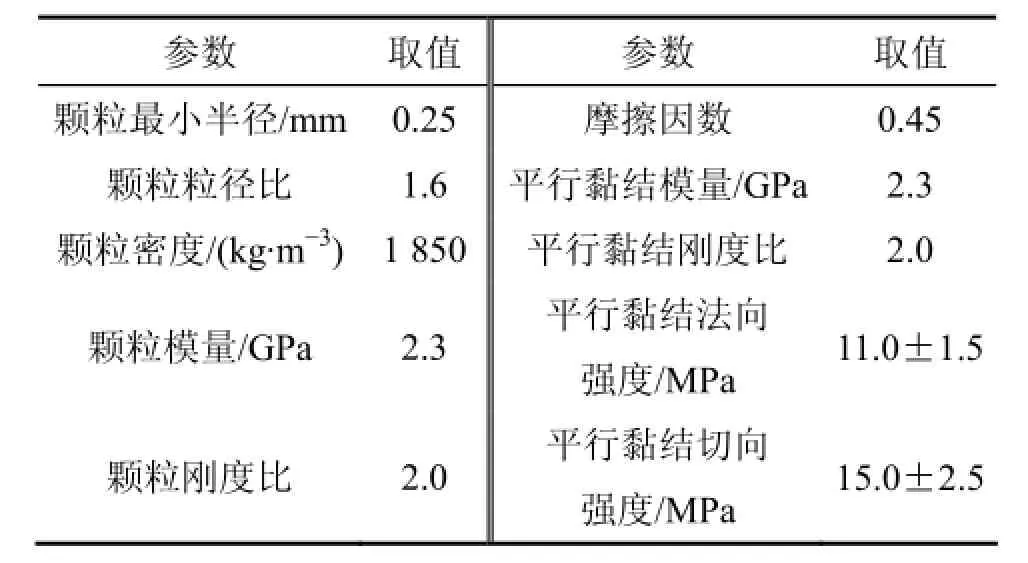
表1　类岩石材料细观参数［20］Table 1 Micro-parameters for rock-like material［20］

图1所示为采用表1所示细观参数模拟获得的完整圆盘试样巴西试验最终破裂模式试验结果与室内试验结果对比。从图1可见：PFC模拟获得的破裂模式试验结果与试验结果相吻合，这表明采用颗粒流程序以及该组细观参数（表1）可以再现圆盘试样巴西试验。在此基础上，进行后续中心直切槽圆盘试样颗粒尺寸效应分析。

图1　完整类岩石材料圆盘试样破裂模式［19］Fig. 1　Failure modes of intact disc specimen［19］

1.2模拟方案设计

本文中，中心直切槽圆盘直径D为50 mm，切槽长充2a设计为15 mm，即a/R=0.3，如图2所示。ATKINSON等［21］经过分析认为中心直切槽圆盘试样的断裂韧度可由下式求得：

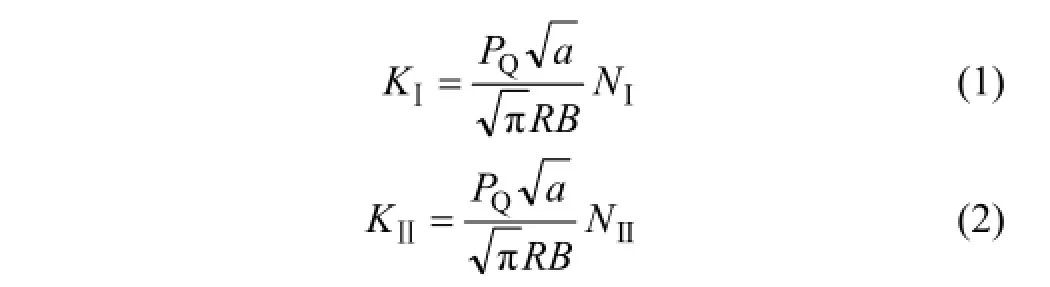
式中：KⅠ和KⅡ分别为Ⅰ型和Ⅱ型断裂韧度；a为切槽半长；R为圆盘半径；B为圆盘厚度；PQ为破坏荷载；NⅠ和 NⅡ为量纲一系数。当中心切槽长度相对于圆盘半径较小时（a/R≤0.3），ATKINSON等［21］可将它当作无限介质中的小裂隙处理，并推导了NⅠ和NⅡ的计算公式：

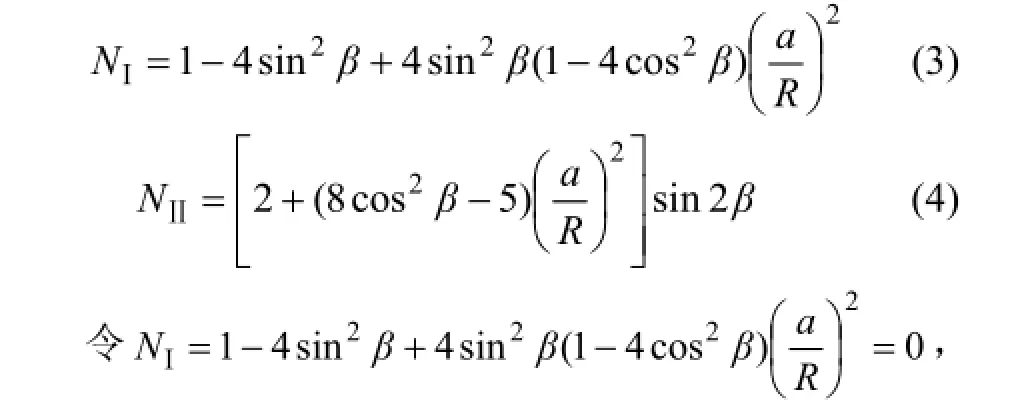
本文设计3种切槽，倾角β分别为0°，27.2°和45.0°，分别对应Ⅰ型加载、Ⅱ型加载和混合型加载。

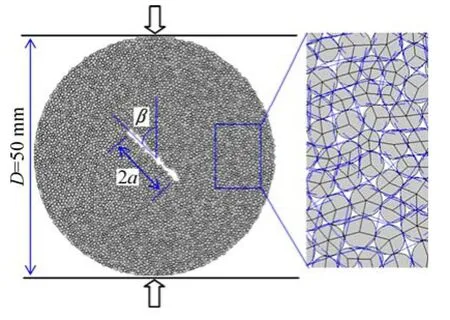
图2　PFC构建的中心直切槽圆盘试样Fig. 2　PFC numerical CSNBD specimen constructed by PFC

为研究颗粒尺寸对中心直切槽圆盘强度和裂纹扩展特征的影响，设计模拟方案，如表2所示。表2中：Rmin为颗粒最小半径；Rmax/Rmin为颗粒最大半径与最小半径的比值；Rave为颗粒平均半径。

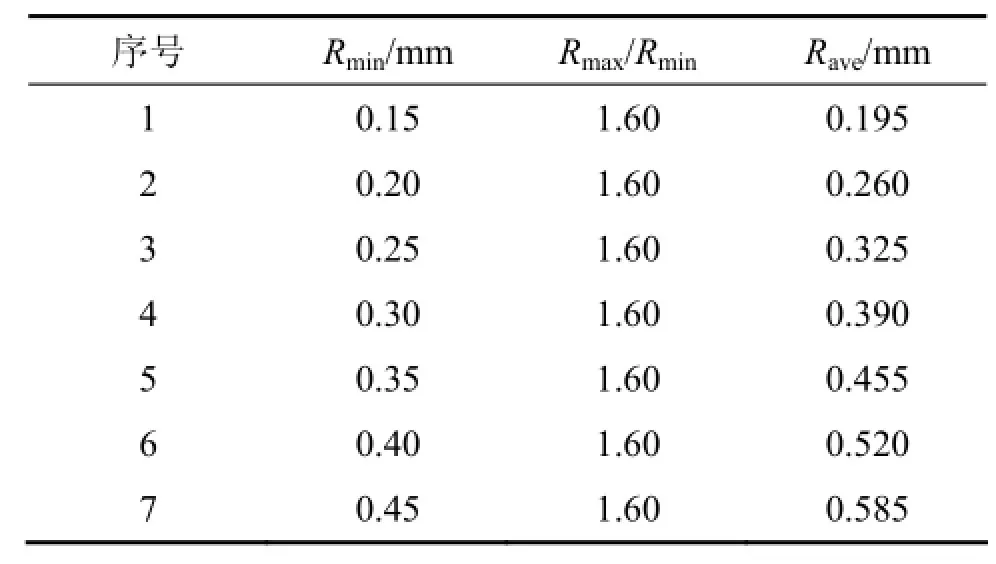
表2　中心直切槽圆盘试样几何参数Table 2 Geometries of CSNBD specimen

2　力学特性分析

2.1荷载-位移曲线

图 3所示为不同颗粒尺寸下的巴西试验荷载-位移曲线。从图 3可见：中心直切槽圆盘试样荷载-位移曲线可以分为线性变形阶段、裂纹萌生及扩展阶段和峰后破坏阶段；β为27.2°和45.0°试样荷载-位移曲线与β为0°试样的荷载-位移曲线相比，呈现更多的跌落。

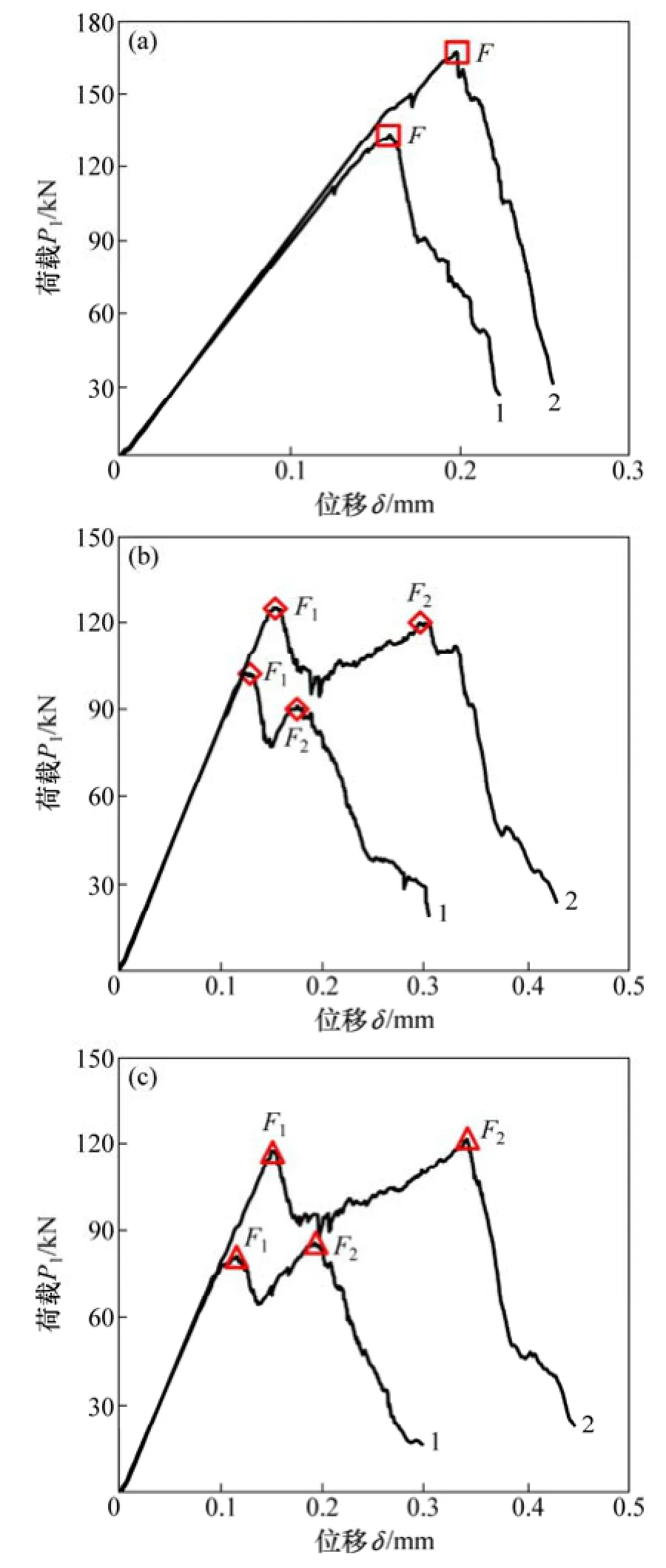
图3　完整中心直切槽圆盘巴西试验荷载-位移曲线Fig. 3　Load-displacement curves of CSNBD specimens

对比图3（a），3（b）和3（c），荷载-位移曲线可以分为典型的3类：type I，为单峰值曲线，其特征在于曲线仅有1个明显的峰值荷载F，如图3（a）所示；type II，为峰值之后软化曲线，其特征在于曲线有2个明显的峰值荷载F1和F2，且F2小于F1，如图3（b）所示；type III，为峰值后强化曲线，其特征在于曲线有2个明显的峰值荷载F1和F2，且F2大于F1，如图3（c）所示。表3所示为中心直切槽圆盘试样荷载-位移曲线类型。

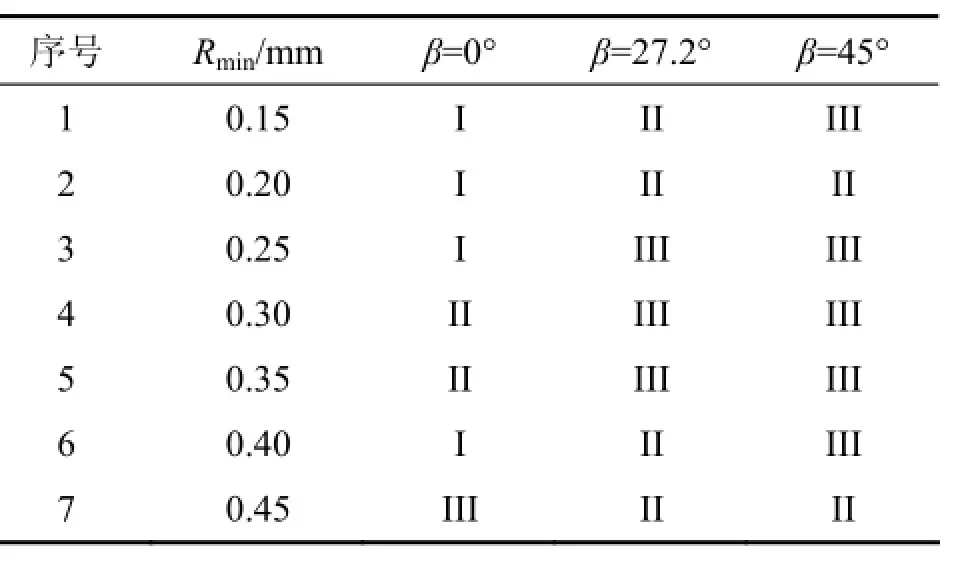
表3　中心直切槽圆盘荷载-位移曲线类型Table 3 Types of load-displacement curves of CSNBD specimens

1） type I 曲线。在线性变形阶段，荷载随着位移的增大呈近似线性增大，该阶段一般不产生裂纹。当进入裂纹萌生及扩展阶段后，荷载随着位移的增大呈非线性增大，该阶段裂纹产生裂纹和裂纹不断扩展，但试样还未破坏。峰值荷载之后，次生裂纹的产生和扩展导致试样承载能力降低，试样最终失稳破坏。

2） type II 曲线。荷载首先随着位移的增大近似呈线性增大到峰值荷载，荷载达到峰值之后，开始跌落。当跌落至一定程度后，由于试样还未完全破裂，还具有较高的承载能力，因此，荷载继续上升，但第2次上升曲线的斜率与初次上升曲线相比较低，这是因为试样内部已经出现了较大损伤。曲线到达第2次峰值后，荷载逐渐降低，试样最终破裂。

3） type III 曲线。与type II 曲线相比，两者最大的区别在于type III 曲线第2次峰值大于第1次峰值。

2.2拉伸强度

从图 3还可以看出：颗粒尺寸对荷载-位移曲线线性变形阶段的斜率无明显影响，而对峰值荷载的影响显著。表4所示为颗粒最小半径对中心直切槽圆盘间接拉伸强度的影响。完整圆盘拉伸强度由下式计算得到：

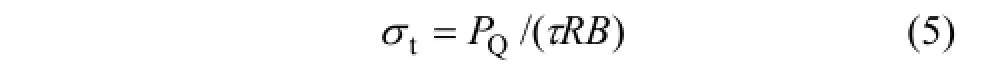
中心直切槽圆盘强度也采用式（5）计算，但该值并非其真实拉伸强度，本文仅将其用于比较。强度衰减因子δ由下式计算：

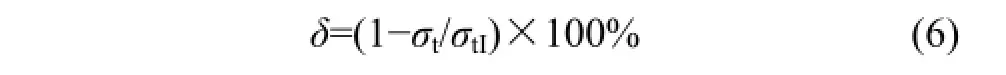
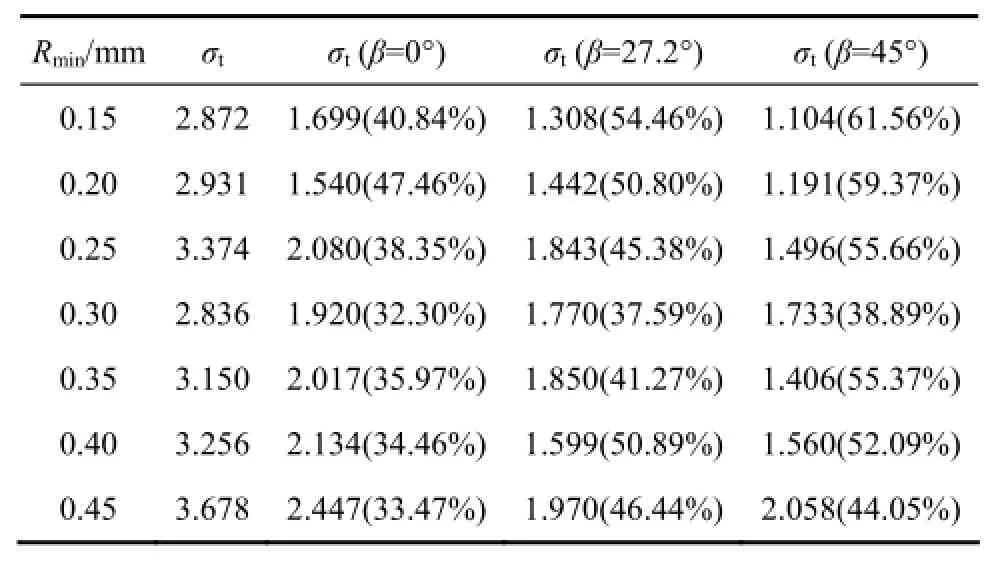
表4　中心直切槽圆盘试样拉伸强度Table 4 Tensile strength of intact and CSNBD specimens

式中：σt和σtI分别为中心直切槽圆盘和完整圆盘试样的拉伸强度。

从表4可见：当倾角β为0°时，拉伸强度分布在1.540 MPa（Rmin=0.20 mm）～2.477 MPa（Rmin=0.45 mm）之间，最小强度衰减因子为32.30%（Rmin=0.30 mm），最大强度衰减因子为47.46%（Rmin=0.20 mm）；当倾角β 为 27.2°时，强度分布在 1.308 MPa（Rmin=0.15 mm）～1.970 MPa（Rmin=0.45 mm）之间，最小强度衰减因子为37.53%（Rmin=0.30 mm），最大强度衰减因子为54.46% （Rmin=0.15 mm）；当倾角β为45°时，强度分布在1.104 MPa（Rmin=0.15 mm）～2.058 MPa （Rmin=0.45 mm ）之间，最小强度衰减因子为38.89%（Rmin=0.30 mm），最大强度衰减因子为61.56%（Rmin=0.15 mm）。

图4所示为圆盘试样拉伸强度与颗粒最小半径之间的关系。从图4可见：中心直切槽圆盘试样拉伸强度显著比完整圆盘试样的低，且降幅与切槽倾角密切相关；当切槽倾角不变时，拉伸强度总体上随着颗粒最小半径的增大而增大；而当颗粒最小半径不变时，拉伸强度随着切槽倾角的增大而减小。

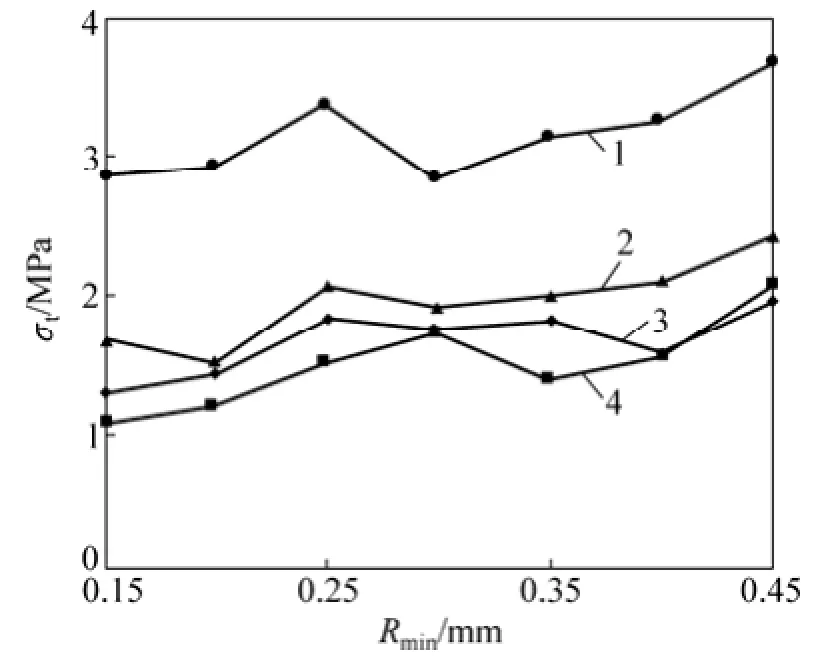
图4　圆盘试样拉伸强度与颗粒尺寸之间的关系Fig. 4　Relationship between tensile strength and particle size

3　裂纹扩展细观机理

3.1宏观破裂模式分析

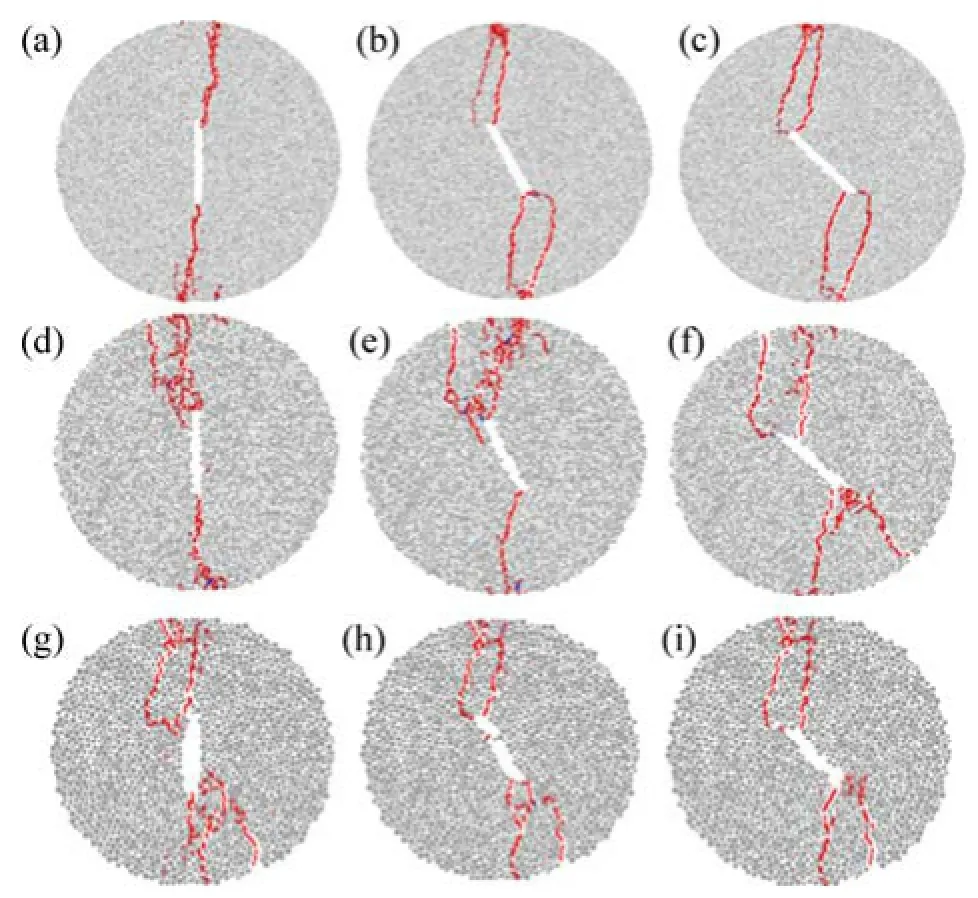
图5　颗粒尺寸对中心直切槽圆盘破裂模式的影响Fig. 5　Effect of particle size on failure mode of CSNBD specimens under Brazilian test

图5所示为颗粒最小半径对中心直切槽圆盘最终破裂模式的影响，仅以颗粒最小半径为0.15，0.30和和0.45 mm为例说明，分别如图5（a），5（b）和5（c）所示。从图5（a）可见：当颗粒最小半径为0.15 mm，倾角β 为0°时，中心直切槽圆盘试样主要发生轴向劈裂破坏，最终破裂为两半，是由切槽两端起裂的2条拉伸裂纹造成的；当倾角β为27.2°时，试样内除了2条从裂隙尖端萌生的翼形裂纹外，还有2条由试样端部萌生的次生裂纹；当倾角β为45°时，破裂模式与倾角β为27.2°试样相似，由翼形裂纹和次生裂纹共同作用导致破坏。从图5（b）可见：当颗粒最小半径增大为0.30 mm，倾角β为0°时，中心直切槽圆盘试样除了裂隙尖端萌生的主裂纹外，还有1条次生裂纹；而当倾角β为27.2°时，试样内有2条翼形裂纹和1条次生裂纹；倾角β 为45°试样是由2条翼形裂纹和2条次生裂纹作用造成试样破裂。需特别注意的是：上部翼形裂纹并非萌生于切槽尖端而是萌生于距切槽尖端一定距离处。从图5（c）可见：当颗粒最小半径增大为0.45 mm，倾角β 为0°时，中心直切槽圆盘试样含有2条切槽尖端萌生的主裂纹和3条试样端部萌生的次生裂纹，切槽下尖端萌生的主裂纹并未扩展至试样的边缘；倾角 β为27.2°和 45.0°中心直切槽圆盘试样破裂模式相似，均为翼形裂纹和次生裂纹共同作用导致试样破裂。对比图5（a），5（b）和5（c）可知：颗粒最小半径对中心直切槽圆盘试样的破裂模式均有较大的影响，且当颗粒最小半径相同时，颗粒最小半径主要影响中心直切槽圆盘中次生裂纹的萌生和扩展。

3.2裂纹扩展过程细观力场演化

为分析中心直切槽圆盘试样裂纹萌生及扩展过程以及对应阶段试样内部细观力场的演化规律，对巴西试验模拟过程进行裂纹及细观力场跟踪监测。

图6　中心直切槽圆盘裂纹扩展过程与细观力场演化（β=27.2°，Rmin=0.15 mm）Fig. 6　Crack propagation processes and evolution of micro-force fields of CSNBD specimen （β=27.2°， Rmin=0.15 mm）

当颗粒最小半径为0.15 mm，切槽倾角为27.2°时，中心直切槽圆盘试样裂纹扩展过程如图6所示。图6同时给出了各裂纹扩展阶段对应的试样内颗粒间接触力场和平行黏结力场的演化。在接触力场中，黑色线段表示压力，线段粗细表示力的大小，标注数值为最大接触力；在平行黏结力场中，深色表示压力，浅色表示拉力，线段越粗，表示平行黏结力越大，标注数值为最大平行黏结力。从图6可见：对于切槽倾角β 为 27.2°的圆盘试样，当荷载为 92.34 kN（89.90%PQ）时，首先是切槽上尖端萌生裂纹。从接触力分布图可以看出：在切槽尖端出现应力集中。从平行黏结力分布图可见：平行黏结力拉应力集中区分布在切槽尖端与试样端部之间区域，平行黏结压应力集中区分布在切槽尖端。试样端部出现应力集中现象是由于加载板与试样接触形成的；当荷载继续增大至102.72 kN即劈裂荷载时，切槽下尖端也开始萌生裂纹。观察此时的平行黏结力分布可以发现：切槽阶段的压应力集中没有消失，而拉应力集中会随着裂纹的扩展不断地转移；劈裂荷载之后荷载逐渐降低；当荷载降至 78.06 kN（峰后 76.0%PQ）时，2条翼形裂纹已经扩展至试样端部。从平行黏结力分布图可见：随着裂纹充分扩展至试样端部，平行黏结拉应力集中区已经消失，而且在翼形裂纹周围平行黏结压应力占绝对优势。从翼形裂纹扩展路径可见：翼形裂纹最初与加载方向呈夹角，裂纹扩展至一定长度后逐渐平行于加载方向即最大主应力方向；与此同时，在试样下端部萌生第1条次生裂纹。而后，在荷载水平为78.06 kN（峰后80.41%PQ）时，在试样上端部也萌生了1条次生裂纹。由最终破裂模式可见：次生裂纹逐渐向着切槽尖端方向扩展，且次生裂纹的扩展路径并不光滑。试样最终破裂后，试样内颗粒间接触力和平行黏结力均相对均匀分布，这也意味着在裂纹起裂、扩展至最终破裂的过程中，试样内部细观力场也逐渐由切槽阶段应力集中向整体均匀分布转变。

当最小半径为0.40 mm，切槽倾角为27.2°圆盘试样裂纹扩展过程及相应的接触力、平行黏结力场演化如图7所示。从图7可见：对于切槽倾角β为27.2°圆盘试样，当荷载为120.0 kN（95.93%PQ）时，首先在切槽上尖端萌生初始裂纹，接着在切槽下尖端产生裂纹（对应荷载水平为劈裂荷载125.61 kN）；翼形裂纹扩展路径逐渐平行于加载方向；当荷载到达 113.92 kN（峰后90.69%PQ）时，在试样上端部萌生次生裂纹，次生裂纹逐渐扩展至切槽下尖端；当荷载水平为105.74 kN（峰后84.18%PQ）时，在试样的左上边缘产生第2条次生裂纹，并扩展至切槽上尖端。在裂纹扩展过程中接触力和平行黏结力的演化与图6的类似。

结合图6及图7可见：在切槽倾角相同时，含不同颗粒尺寸中心直切槽圆盘试样裂纹萌生的位置及顺序不同。由以上分析可知颗粒尺寸对次生裂纹的萌生及扩展更为显著。此外，对比图6、图7所示细观力场可见：图6中接触力和平行黏结力的线段明显比图7中的细，但图6中密集程度比图7中的高，这意味着当颗粒最小半径较小（0.15 mm）时，细观应力较低，但应力集中程度较高；当颗粒最小半径较大（0.40 mm）时，细观应力较大，但应力集中程度较低。由此可见，可以借助细观力场值分析中心直切槽圆盘试样拉伸强度随颗粒尺寸的变化规律。图8所示为不同加载方式下拉伸强度与劈裂荷载时圆盘试样内最大平行黏结力的关系曲线。从图8可见：最大平行黏结力与抗拉强度总体上呈正比关系，即最大平行黏结力越大，则拉伸强度越大。

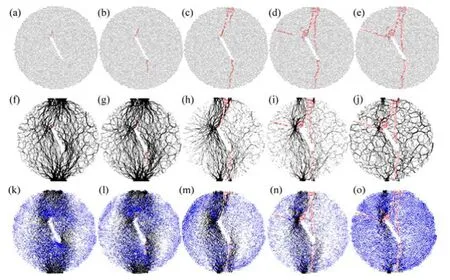
图7　中心直切槽圆盘裂纹扩展过程与细观力场演化（β=27.2°，Rmin=0.40 mm）Fig. 7　Crack propagation process and evolution of micro-force field of CSNBD specimen （β=27.2°， Rmin=0.40 mm）

3.3裂纹扩展过程中微裂纹发育

为揭示中心直切槽圆盘试样裂纹扩展过程中微裂纹发育特征，在模拟过程中对微裂纹数目进行统计，以期建立裂纹扩展过程微裂纹与宏观裂纹扩展之间的关系。图9所示为中心直切槽圆盘裂纹扩展过程中微裂纹发育情况，其中，图9（a）和9（b）中标注的裂纹产生顺序分别见图6和图7。从图9可见：在加载初期，试样内基本无微裂纹产生；当加载至一定荷载后，试样内才开始逐渐有微裂纹萌生。根据荷载-位移-微裂纹曲线之间的关系可知：当荷载曲线发生1个较显著的跌落，对应1次较显著的微裂纹数目，在微裂纹累计曲线上相应产生1次陡增现象，这意味着试样内快速产生了较多的微裂纹。另外，观察宏观裂纹与微裂纹增长速率之间的关系可知，当试样中产生1条显著的宏观裂纹时对应的微裂纹增长速率明显较大。需要注意到的是：图9（a）中产生裂纹1时对应的微裂纹增长速率近似为0。这是因为标注的裂纹1为一定数量的微裂纹聚合在一起形成的肉眼可见的宏观裂纹（见图6（a）），标注时间稍滞后于其真正萌生时间。

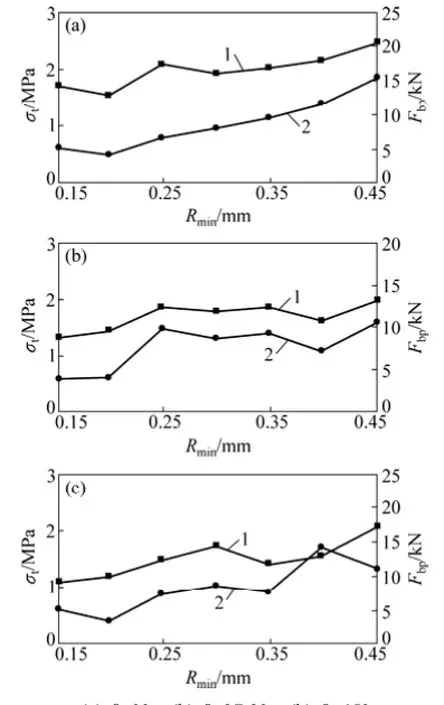
图8　拉伸强度与最大平行黏结力之间的关系Fig. 8　Relationship between tensile strength and the maximum parallel bond force

图 10所示为中心直切槽圆盘试样最终破裂时微裂纹总数柱状图，以探究微裂纹总数与颗粒尺寸之间的关系。从图10可见：当切槽倾角β为0°和27.2°时，裂纹总数总体上随着颗粒尺寸的增大呈减小趋势；而当切槽倾角β为45°时，微裂纹总数与颗粒最小半径之间无明显关系。此外，微裂纹总数虽然有一定的差异，但总体上还保持在1个数量级内（100～400之间）。由此可见：在本次模拟范围内，颗粒最小半径变化时对破裂程度不会产生非常明显的改变。

3.4裂纹扩展过程能量演化

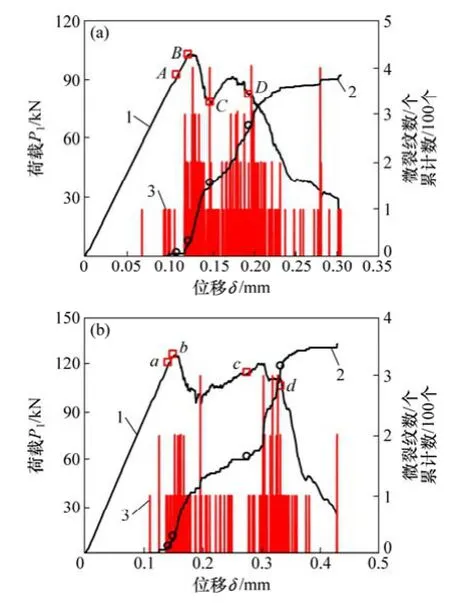
图9　中心直切槽圆盘裂纹扩展过程微裂纹演化Fig. 9　Evolution of micro-cracks during macro-crack propagation process

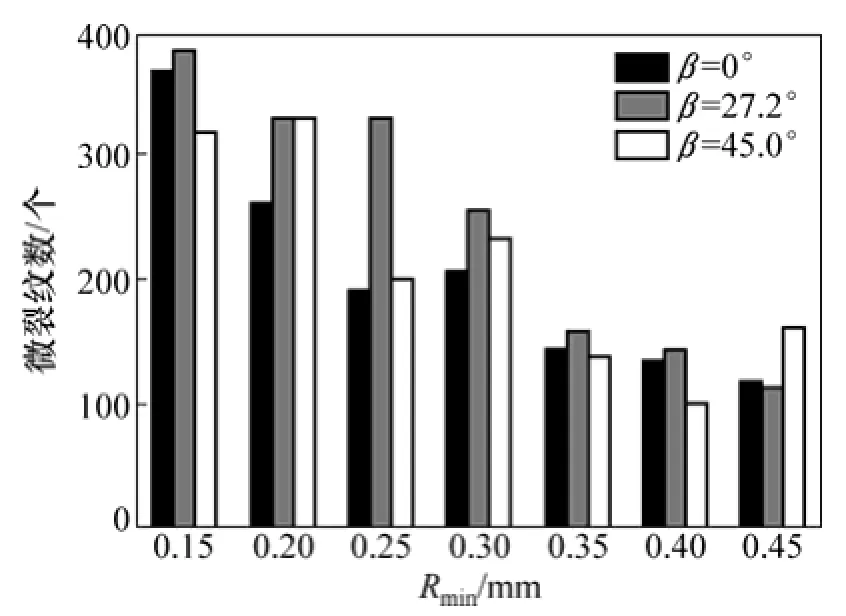
图10　中心直切槽圆盘裂纹总数与颗粒尺寸之间的关系Fig. 10 Relationship between crack number and particle size for CSNBD specimens

在模拟过程中，对各种能量进行追踪，以探讨裂纹扩展过程中能量演化规律，进一步加深对裂纹扩展机制的认识。图11所示为中心直切槽圆盘试样加载过程中能量演化。其中，边界能为边界所作的功即总输入能。从图11可见：边界能在加载过程中持续增大，但其增大的速率会随着加载阶段的不同有所区别。在加载初期，边界能较小且其增长速率较低。这是因为加载初期所需要的能量较低。随着荷载的持续增大，边界能增长速率较快，这是因为该阶段试样克服颗粒之间的黏结，不断有裂纹的产生和扩展，在最后破裂阶段之前，边界能增长速率有所减缓。黏结能是克服颗粒间黏结所作的功，裂纹产生之后在应变能的作用下扩展。摩擦能在加载到一定程度之后才出现，这是因为摩擦能为裂纹摩擦作用总和，在试样内萌生微裂纹之后，摩擦能才起作用，摩擦能随着裂纹的扩展逐渐增大。动能很小，几乎贴着轴线，意味着颗粒的运动程度低，试样的破裂不剧烈。

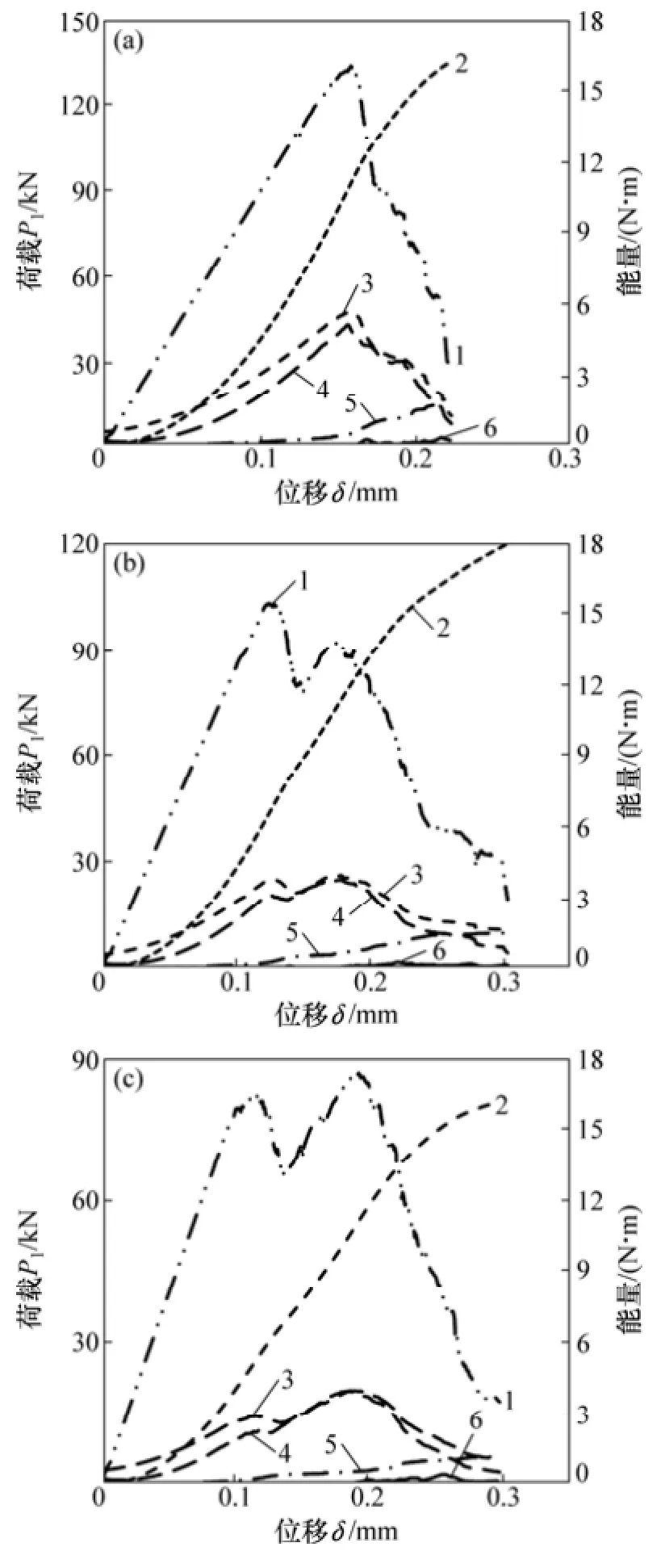
图11　中心直切槽圆盘裂纹扩展过程能量演化Fig. 11 Evolution of energy during macro-crack propagation process

为分析中心直切槽圆盘试样拉伸强度与总输入能之间的关系，绘制边界总能与拉伸强度关系曲线，如图12所示。从图12可见：中心直切槽圆盘试样中边界总能与抗拉强度总体上呈现为正比关系，即边界能越大，则拉伸强度越大。

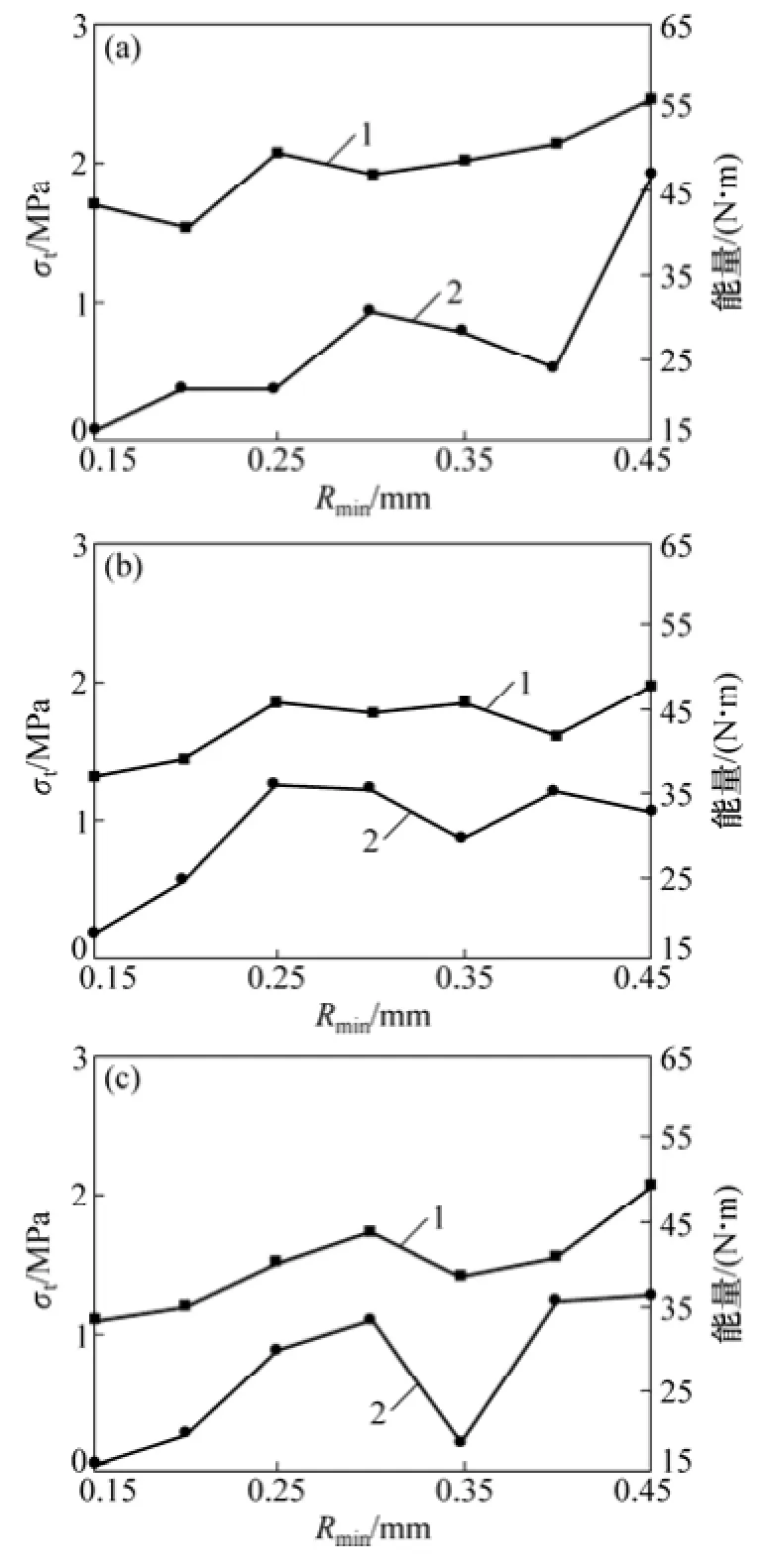
图12　拉伸强度与边界能之间的关系Fig. 12 Relationship between tensile strength and boundary energy

4　结论

1） 含不同切槽倾角和颗粒半径中心直切槽圆盘试样的荷载-位移曲线可分为 3种形式，分别为单峰值曲线（type I），首次峰值之后软化曲线（type II）以及首次峰值之后强化曲线（type III）。

2） 中心直切槽圆盘试样拉伸强度显著比完整圆盘试样的低，且降幅与切槽倾角密切相关。当切槽倾角不变时，拉伸强度总体上随着颗粒最小半径的增大而增大；而当颗粒最小半径不变时，拉伸强度总体上随着切槽倾角的增大而减小。

3） 当切槽倾角相同时，不同颗粒半径中心直切槽圆盘试样破裂模式显著不同。模拟结果显示，颗粒尺寸主要影响中心直切槽圆盘试样中次生裂纹的萌生和扩展。

4） 边界对圆盘试样作功，首先克服颗粒之间的黏结以产生裂纹，裂纹在应变能的作用下不断扩展。在裂纹产生之后，摩擦才开始起作用。颗粒的运动程度很低，因此，动能很小。边界能与抗拉强度总体上呈正比关系，即边界能越大，则拉伸强度越大。

［1］ 杨圣奇， 苏承东， 徐卫亚. 岩石材料尺寸效应的试验和理论研究［J］. 工程力学， 2005， 22（4）： 112-118. YANG Shengqi， SU Chengdong， XU Weiya. Experimental and theoretical study of size effect of rock material［J］. Engineering Mechanics， 2005， 22（4）： 112-118.

［2］ POULSEN B A， ADHIKARY D P. A numerical study of the scale effect in coal strength［J］. International Journal of Rock Mechanics and Mining Sciences， 2013， 63： 62-71.

［3］ ZHANG Q， ZHU H， ZHANG L， et al. Study of scale effect on intact rock strength using particle flow modeling［J］. International Journal of Rock Mechanics and Mining Sciences， 2011， 48：1320-1328.

［4］ AYATOLLAHI M R， AKBARDOOST J. Size and geometry effects on rock fracture toughness： mode Ⅰ fracture［J］. Rock Mechanics and Rock Engineering， 2014， 47（2）： 677-687.

［5］ WONG L N Y， EINSTEIN H H. Crack coalescence in molded gypsum and Carrara marble. Part 1： macroscopic observations and interpretation［J］. Rock Mechanics and Rock Engineering，2009， 42（3）： 475-511.

［6］ WONG L N Y， EINSTEIN H H. Crack coalescence in molded gypsum and Carrara marble. Part 2： microscopic observations and interpretation［J］. Rock Mechanics and Rock Engineering，2009， 42（3）： 513-545.

［7］ WONG L N Y， ZHANG X P. Size effects on cracking behavior of flaw-containing specimens under compressive loading［J］. Rock Mechanics and Rock Engineering， 2014， 47（5）：1921-1930.

［8］ DING Xiaobin， ZHANG Lianyang， ZHU Hehua， et al. Effect of model scale and particle size distribution on pfc3d simulation results［J］. Rock Mechanics and Rock Engineering， 2014， 47（6）：2139-2156.

［9］ 许尚杰， 尹小涛， 党发宁. 晶体及矿物颗粒大小对岩土材料力学性质的影响［J］. 岩土力学， 2009， 30（9）： 2581-2587. XU Shangjie， YIN Xiaotao， DANG Faning. Mechanical characteristics of rock and soil affected by particle size of crystal and mineral［J］. Rock and Soil Mechanics， 2009， 30（9）：2581-2587.

［10］ KOYAMA T， JING L. Effects of model scale and particle size on micro-mechanical properties and failure processes of rocks： a particle mechanics approach［J］. Engineering Analysis with Boundary Elements， 2007， 31（5）： 458-472.

［11］ YANG B， JIAO Y， LEI S. A study on the effects of microparameters on macroproperties for specimens created by bonded particles［J］. Engineering Computations， 2006， 23（6）：607-631.

［12］ FAKHIMI A， VILLEGAS T. Application of dimensional analysis in calibration of a discrete element model for rock deformation and fracture［J］. Rock Mechanics and Rock Engineering， 2007，40（2）： 193-211.

［13］ POTYONDY D O， CUNDALL P A. A bonded-particle model for rock［J］. International Journal of Rock Mechanics and Mining Sciences， 2004， 41（8）： 1329-1364.

［14］ CUNDALL P A， STRACK O D L. A discrete numerical model for granular assemblies［J］. Geotechnique， 1979， 29（1）： 47-65.

［15］ 黄彦华， 杨圣奇. 非共面双裂隙红砂岩宏细观力学行为颗粒流模拟［J］. 岩石力学与工程学报， 2014， 33（8）： 1644-1653. HUANG Yanhua， YANG Shengqi. Particle flow simulation on marco-and meso-mechanical behavior of red sandstone containing two pre-existing non-coplanar fissures［J］. Chinese Journal of Rock Mechanics and Engineering， 2014， 33（8）：1644-1653.

［16］ 杨圣奇， 黄彦华， 刘相如. 断续双裂隙岩石抗拉强度与裂纹扩展颗粒流分析［J］. 中国矿业大学学报， 2014， 43（2）： 220-226. YANG Shengqi， HUANG Yanhua， LIU Xiangru. Particle flow analysis on tensile strength and crack coalescence behavior of brittle rock containing two pre-existing fissures［J］. Journal of China University of Ming and Technology， 2014， 43（2）：220-226.

［17］ 邵磊， 迟世春， 王振兴. 基于裂缝扩展的堆石料流变细观模型［J］. 岩土工程学报， 2013， 35（1）： 66-75. SHAO Lei， CHI Shichun， WANG Zhenxing. Rheological model for rockfill based on sub-critical crack expansion theory［J］. Chinese Journal of Geotechnical Engineering， 2013， 35（1）：66-75.

［18］ 刘广， 荣冠， 彭俊， 等. 矿物颗粒形状的岩石力学特性效应分析［J］. 岩土工程学报， 2013， 35（3）： 540-550. LIU Guang， RONG Guan， PENG Jun， et al. Mechanical behaviors of rock affected by mineral particle shapes［J］. Chinese Journal of Geotechnical Engineering， 2013， 35（3）： 540-550.

［19］ 蒋明镜， 陈贺， 刘芳. 岩石微观胶结模型及离散元数值仿真方法初探［J］. 岩石力学与工程学报， 2013， 32（1）： 15-23. JIANG Mingjing， CHEN He， LIU Fang. A microscopic bond model for rock and preliminary study of numerical simulation method by distinct element method［J］. Chinese Journal of Rock Mechanics and Engineering， 2013， 32（1）： 15-23.

［20］ 黄彦华， 杨圣奇. 孔槽式圆盘破坏特性与裂纹扩展机理颗粒流分析［J］. 岩土力学， 2014， 35（8）： 2269-2277. HUANG Yanhua， YANG Shengqi. Particle flow simulation on fracture characteristics and crack propagation mechanism of holed-cracked Brazilian disc specimen［J］. Rock and Soil Mechanics， 2014， 35（8）： 2269-2277.

［21］ ATKINSON C， SMELSER R E， SANCHEZ J. Combined mode fracture via cracked Brazilian disk test［J］. International Journal of Fracture， 1982， 18（4）： 279-291.

（编辑 陈灿华）

Study on particle size effects on strength and crack coalescence behavior of rock during Brazilian splitting test

HUANG Yanhua1， YANG Shengqi1， 2， JU Yang1， ZHOU Xiaoping3， ZHAO Jian1， 4

（1. State Key Laboratory for Geomechanics and Deep Underground Engineering，China University of Mining and Technology， Xuzhou 221116， China；2. School of Mechanics and Civil Engineering， China University of Mining and Technology， Xuzhou 221116， China；3. School of Civil Engineering， Chongqing University， Chongqing 400045， China；4. Department of Civil Engineering， Monash University， Melbourne VIC 3800， Australia）

A discrete element disc specimen model was constructed using a set of microscopic parameters which were calibrated by the experimental results of intact rock-like material disc specimen during Brazilian splitting test in particle flow code （PFC）.Then PFC was adopted to simulate Brazilian test for central straight notched Brazilian disc （CSNBD）specimens. The effects of particle size on the load-displacement curves， tensile strength and failure mode of CSNBD specimens were analyzed， and the evolution laws of meso-force， micro-crack and energy during the process of macro-crack initiation， propagation and coalescence of CSNBD specimen were revealed. The results show that complete axial load-displacement curves can be divided into three types， i.e.， single peak（type I）， softening after first-peak（type II） and hardening after first-peak（type III）.Compared with the intact disc specimen， the tensile strength of CSNBD specimen all decreases， and the reducing extent is related to the notch angle and particle size. By keeping the notch angle constant， the tensile strength shows a downwards trend with the increase of particle size， while keeping the particle size constant， the tensile strength decreases with the increase of the notch angle. The failure modes of CSNBD specimens are dependent on particle size. The particle size mainly affects the initiation and propagation of secondly cracks. The power produced by boundary wall is firstly used to overcome the bond among particles. After the crack initiation， friction energy begins to work， and the crack is propagated by strain energy. Since the particle moves slowly， the kinetic energy is small. The boundary energy is positively correlated with the tensile strength， i.e.， the bigger boundary， the higher tensile strength.

rock mechanics； Brazilian test； central straight notched disc specimen； particle size effect； particle flow code

TU45

A

1672-7207（2016）04-1272-10

10.11817/j.issn.1672-7207.2016.04.025

2015-05-04；

2015-06-25

江苏省杰出青年基金资助项目（BK20150005）；国家自然科学基金资助项目（41272344）；2014江苏省双创团体项目（BK20150005）（Project （BK20150005） supported by the National Natural Science Foundation of Jiangsu Province for Distinguished Young Scholars； Project （41272344） supported by the National Natural Science Foundation of China； Project （BK20150005） supported by the Team Program of 2014 Jiangsu Innovation and Entrepreneurship）

杨圣奇，教授，博士生导师，从事深部岩石力学与地下工程研究；E-mail：yangsqi@hotmail.com