基于时段聚类的峰谷电价时段确定方法研究

赵 明，董 力，李孟阳，高赐威，喻 洁（.云南省电力试验研究院（集团）有限公司科学研究院，昆明 650000；.东南大学 电气工程学院，南京 0096）

基于时段聚类的峰谷电价时段确定方法研究

赵 明1，董 力2，李孟阳1，高赐威2，喻 洁2
（1.云南省电力试验研究院（集团）有限公司科学研究院，昆明 650000；2.东南大学 电气工程学院，南京 210096）

合理的峰谷电价设置能够极大地改善负荷特性。在考虑用户需求响应的基础上，建立了峰谷时段动态调整模型框架，由时段划分、时段调整和效果评估三个模块组成。预处理日负荷数据后，通过排序法和K-means聚类法划分峰谷平时段，采用剔除或介绍友时段的方法处理孤立时段，比较时段调整前后设定指标的变化情况评判时段调整效果，发现K-means聚类法更能反映季节对用户用电行为产生的影响。某地区实例分析表明，当时段-电价曲线与峰谷时段切合度较高时，可以削峰填谷，提高机组利用率，有利于激励更多的需求响应资源；反之，则会使得负荷特性指标恶化。

需求响应；峰谷电价；时段调整；排序分配；K-means聚类分配

峰谷电价是一项重要的基于价格的需求响应手段［1］，它通过划分峰谷平时段，设置不同的时段电价来引导用户将一部分峰时段用电转移到平时段或谷时段使用，从而削峰填谷，降低电网调峰压力和发供电成本，提高机组利用率和系统稳定性。

峰谷时段的关键问题分为时段划分和电价制定两部分，实施效果主要取决于用户的响应度。国内外基于需求响应机制就峰谷时段电价问题展开了研究。文献［2］基于时段峰、谷隶属度的模糊聚类理论，提出了一种考虑用户需求响应的时段划分模型。文献［3］结合运行状况建立了发电成本关于负荷的函数，根据该函数在负荷点的突变特征划分时段区间。

我国在大多数省份已经实施了峰谷电价，在江苏、浙江、北京等省市峰谷电价的实施已有十多年的历史。在此过程中，电价经过多次调整，但是往往是基于煤价变动引起的电价大小的调整，几乎没有针对峰谷时段的调整，如江苏当前执行的峰谷电价时段与2002年最初制定的时段无异，广东、云南等地也有类似的现象。这表明我国当前的销售电价变化主要是由发电成本变化触发的，而对负荷特性的改变所引起的峰谷时段的变化没有做合理的反映。

本文针对峰谷电价时段优化的现实需要建立了考虑用户需求响应的时段调整模型框架，分别采用排序分配法和K-means聚类法对时段进行划分，剔除孤立时段的毛刺现象，得出最终的时段调整方案，并对调整后的时段分配情况进行评估。时段-电价曲线和时段-负荷曲线的切合度，可反映实施峰谷电价机制的有效性。

1 峰谷时段调整模型框架

基于时段聚类的确定峰谷电价时段的模块框架先对负荷数据进行峰谷时段划分，然后与已有时段进行对比，提出调整方案，最后进行方案评估，具体由以下3个模块组成，如图1所示。

图1 峰谷时段调整流程图

（1）基于负荷数据的时段划分：对原始负荷数据中的无效数据和缺失数据进行剔除和补充，得到初始数据。采用排序分配法和K-means聚类法分析初始数据的负荷峰谷特性，划分峰谷时段。根据这两种方法的优缺点，可以结合具体情况交叉使用。

（2）时段调整：对比未调整的与时段划分模型输出的峰谷时段匹配情况，拟定初步的时段调整方案，对初步方案中的孤立时段再修正，用剔除或寻找友时段的方法处理孤立时段，得到最终方案。

（3）效果评估：设定评估指标，如峰谷时段不匹配率η、峰谷电量比α、总电费变化率δ等，分析峰谷时段调整前后的指标变化情况。

2 基于负荷数据的时段划分模块

2.1 数据预处理

由于负荷原始数据可能出现数据缺失或无效现象，为保证后续计算的可靠性，需要对其进行一定的预处理工作。对于数据缺失现象，采用均值法，即对缺失数据前后的已知数值取平均值，填补缺失数据，可以验证若无尖峰情况此处理方法造成的误差很小。均值法的公式为

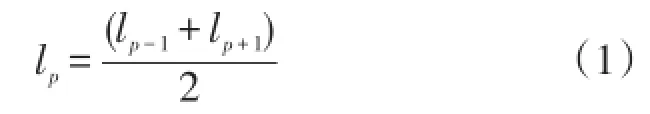
式中：lp表示填补的负荷数据，lp-1和lp+1表示缺失数据前后已知的2个负荷值。

对于数据无效现象，采用剔除法。判断数据是否为无效数据的方法是检验每个数据值与其前后数据平均值的相近度，假设相近度S小于0.1时，认为此数据点无效。剔除该点，用处理缺失数据的均值法在此处填充新的数据点。设lp为根据前后两个已有数据计算出的平均值，即，li为原始数据值，相近度公式为

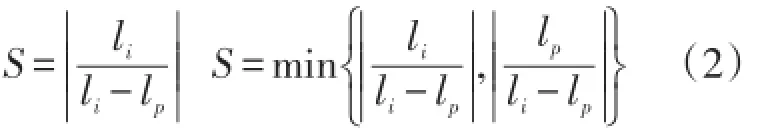
2.2 负荷-电价匹配分析

对预处理后的初始负荷数据进行特性划分，分析峰平谷时段匹配度。调整周期人为设定，如月度、季度、年度等，为了保证用电结构的稳定性，时段调整不宜太过频繁，因此实际应用中常以年度为调整周期。将调整周期内的日负荷值抽象处理为24个时点对应的平均负荷值，计算公式为

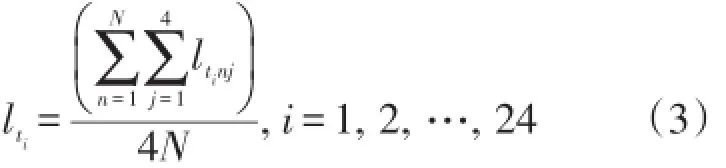
式中：lti表示24个时点对应的负荷值，ltinj表示调整周期内对应时点的日负荷值，N为调整周期总天数。因此，典型日负荷曲线上各时点组成的时点集合为T=｛t1，t2，…，t24｝，各时点对应的负荷值集合为L=｛lt1，lt2，…，lt24｝。

本文采用排序分配和K-means聚类2种峰谷时段划分方法。排序分配法是提前确定峰谷平各自的时段数，用排序法划分。而K-means聚类法是在不确定峰谷平时段数的前提下，仅通过数据特性进行聚类分析。

（1）排序分配法

峰谷平时段数可具体指定。假设峰谷平分别为24 h的平均分配，则负荷值最高的8 h对应峰时段，最低的8 h对应谷时段，剩余的8 h对应平时段。

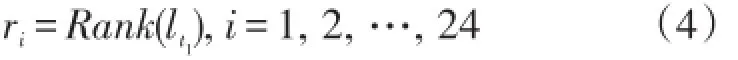
式中：ri为24小时的升序编号ri=1，2，…，24，再按照排列顺序平均划分为峰谷平3个时段，即

（2）K-means聚类分配法

K-means聚类法给定一个数据点集合和需要的聚类数目，根据特定的距离函数通过迭代将数据点移入各聚类域中，实现步骤为：

步骤1：给定24个时段的负荷样本数据集，令迭代次数为R，指定聚类数为3，即峰、平、谷，随机选取3个负荷值作为初始聚类中心Cj（r），其中 j=1，2，3；r=1，2，…，R。

步骤2：计算样本空间中每个数据对象与初始聚类中心的相似度距离D（Xi，Cj（r），其中i=1，2，…，24，形成簇W ，如果满足式（6）

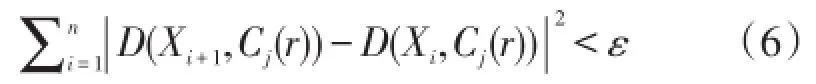
则Xi∈Wj，Xi记为ω；其中ε为任意给定的正数。

步骤3：计算3个新的聚类中心，计算公式为

聚类准则函数值为

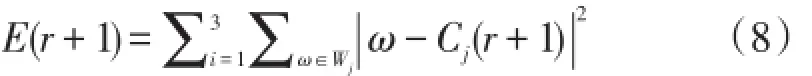
步骤4：判断聚类是否合理，判断公式为

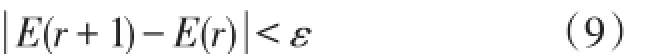
若合理则迭代终止，若不合理则返回步骤2、3继续迭代。

用K-means算法将24个时段的负荷平均值进行聚类分析，结果为

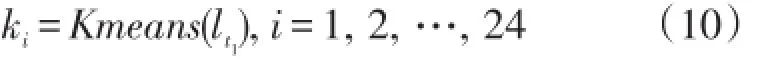
式中：ki为24个时段对应的类别数，聚类后划分为峰谷平3个时段

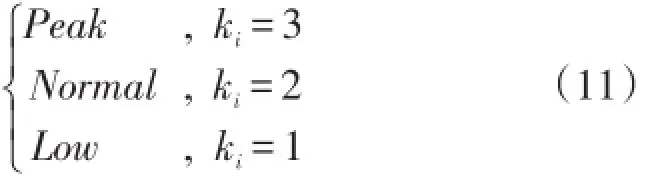
通过以上2种方法分别得到峰谷平时段数组Dr=｛dr1，dr2，…，dr24｝和Dk=｛dk1，dk2，…，dk24｝，未调整的峰谷时段数组为K=｛k1，k2，…，k24｝，3、2、1这3个数值分别对应峰、平、谷3个时段

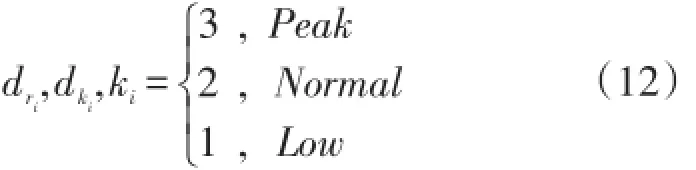
将时段划分情况与未调整时段进行对比，得到匹配数组Match=｛m1，m2，…，m24｝，即

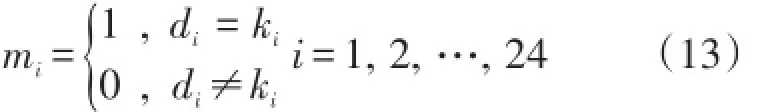
式中：di=dri或di=dki，且1代表匹配，0代表不匹配。

3 时段调整模块

3.1 初步修正

根据24 h匹配数组的定义初步得到结论：需要对数组中匹配数值为0对应的时段进行峰谷平调整。给出初步时段修正方案R=｛r1， r2，…，r24｝，表示为

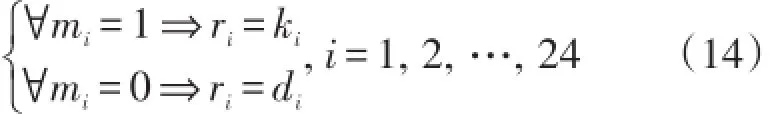
式中：ri表示初步方案中的时段分类。

3.2 再修正

由于初步的峰谷平时段修正方案中可能出现孤立时段的毛刺现象，而在实际操作过程中，不建议仅为孤立时段变换峰谷电价。因此，需要对初步的修正方案进行再修正，具体方法为：

方案1：还原孤立时段原始状态。若时段调整后导致该时段或其前后时段成为孤立时段，则还原该时段原始的峰谷平类别。

方案2：合理改变孤立时段前后时段状态，为孤立时段介绍友时段。

验证调整周期选择的合理性。确定最终的时段调整方案后，缩短调整周期重新划分时段，比较各月度时段分配的不匹配率θ。

若不匹配率较小，小于设定值θs，则最终的时段调整方案可不做细化；若较大，则需要按照缩短后的周期重设部分峰谷时段。时段划分一般以年为周期，若选取一年的日负荷数据进行峰谷时段调整后，不匹配率仍然不能满足要求，则可以缩短调整周期，如：半年、季度、月度等，时段调整的方法与之前一致，直到不匹配率满足要求为止。

4 效果评估模块

设定时段调整的效果评估指标，如：峰谷时段不匹配率θ、峰谷电量比α、总电费变化率δ等，对比调整前后对应指标值是否有所改善，从而分析时段调整的有效性。

（1）峰谷时段不匹配率θ

绘制一段时期的时段-电价曲线和时段-负荷曲线（调整周期内每小时平均负荷），对比峰谷平时段匹配情况，统计不匹配小时数H，定义峰谷电价时段不匹配率θ为

如果时段调整后不匹配率明显降低，则表明电价设定较好地反映了负荷特性。

（2）峰谷电量比α

峰谷电量比指用户峰时段的平均负荷与谷时段的平均负荷的比值，比值大小反映了机组的利用率，计算公式为

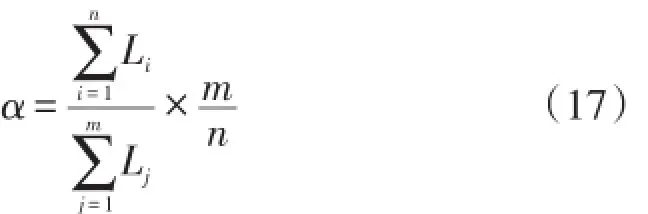
式中：Li和Lj分别为峰时段和谷时段各小时平均负荷，n和m分别为峰时段和谷时段时长。

如果时段调整后峰谷电量比值明显降低，则表明机组的利用率有所提高。

（3）总电费变化率δ

峰谷时段的调整会改变各时段对应的电价，而电价是引导用户改变自身用电行为最直接有效的方式。定义所有电力用户缴纳的电费变化率δ为

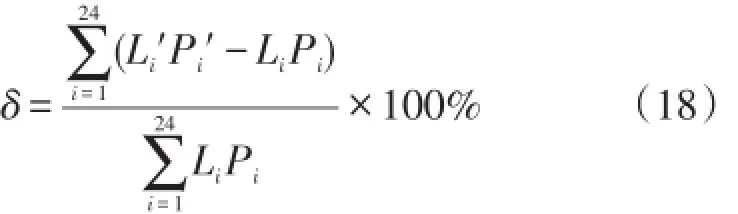
式中：Li，Li′和Pi，Pi′表示时段调整前后各时段的负荷值以及对应的电价。

5 实例分析

根据模型框架中3个子模块的具体实现方法，结合2011年某省全年的日负荷值和峰谷电价时段划分，提出最终的时段调整修正方案，具体分析步骤如下。

首先预处理原始负荷数据。用均值法填补缺失数据，剔除法找出并去除无效数据，并用均值法替换为有效数据。

分别以年度、春夏季、秋冬季为时段调整周期，利用公式（3）将数据处理为24个时点对应的平均负荷值，绘制时段-负荷曲线和时段-电价曲线，如图2所示。

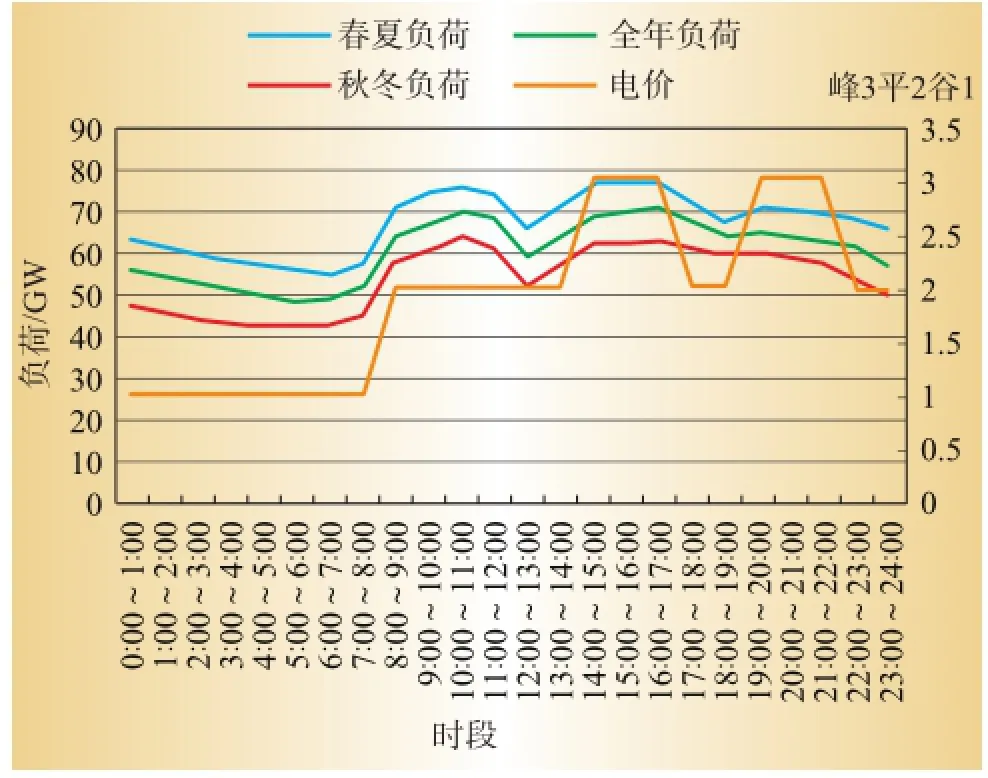
图2 2011年某省时段-负荷和时段-电价曲线

图中春夏季、秋冬季以及全年的负荷曲线随时段变化趋势相近，结合实际情况，选取全年为时段调整周期。

（1）排序划分法

抽象处理全年日负荷数据，得到与24个时段相对应的平均负荷值，并按升序排列，按照峰平谷分别8个时段的方法平均分配，结果如表1所示。

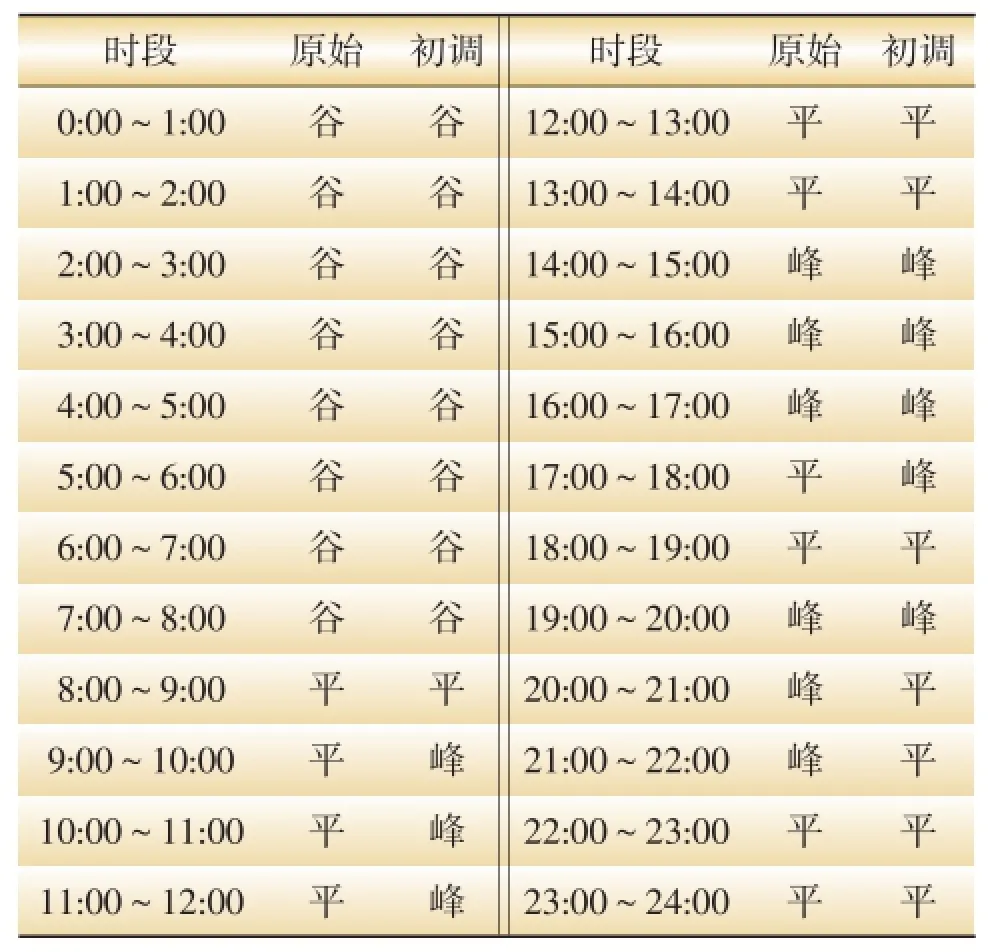
表1 2011全年初始的排序法时段划分表

由表1可知，9：00～12：00，17：00～18：00，20：00～22：00这6个时段需要进行调整，其中若修改时段9：00～10：00，17：00～18：00，20：00～21：00，则会出现孤立时段8：00～9：00和18：00～20：00。2种再修正方案为：

方案1：将9：00～10：00，17：00～18：00，20：00～21：00时段的状态分别还原为平、平、峰时段。

方案2：为孤立时段介绍友时段。根据孤立对象前后时段的峰谷分布及不匹配情况，分别将8：00～9：00，18：00～19：00，19：00～20：00变为峰、峰、平时段。

由于用方案1和方案2对初始时段调整方案再修正后，全年的峰谷时段不匹配率均为12.5%，为细化方案效果，将周期缩短为月度重新划分时段。表2列举了按月度划分时段与按方案1修正后分配时段的不匹配率，月度总不匹配度为19.44%。

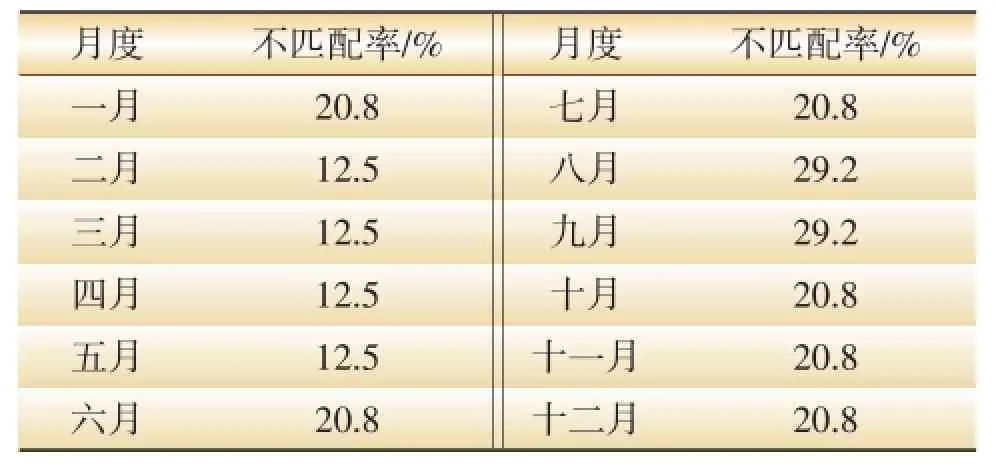
表2 按月度划分时段与方案1的不匹配情况

由表2可知，方案1修正后的不匹配率较高，需辅以方案2进行修正。方案2中若将8：00～9：00改为峰时段，月度总不匹配率为19.79%；若将18：00～19：00改为峰时段，月度总不匹配率为15.625%；若将19：00～20：00改为平时段，月度总不匹配率为14.58%。

因此，综合方案1、方案2，还原9：00～10：00为平时段，并调整18：00～19：00为峰时段，19：00～20：00为平时段，使其分别成为17：00～18：00，20：00～21：00时段的友时段。此时，年度的峰谷时段不匹配率为12.5%，月度总不匹配率为6.59%，修正后峰谷时段的不匹配率大大降低。表3列举了按月度划分的时段分配与最终调整方案的不匹配率，最终的时段调整方案如表4所示。

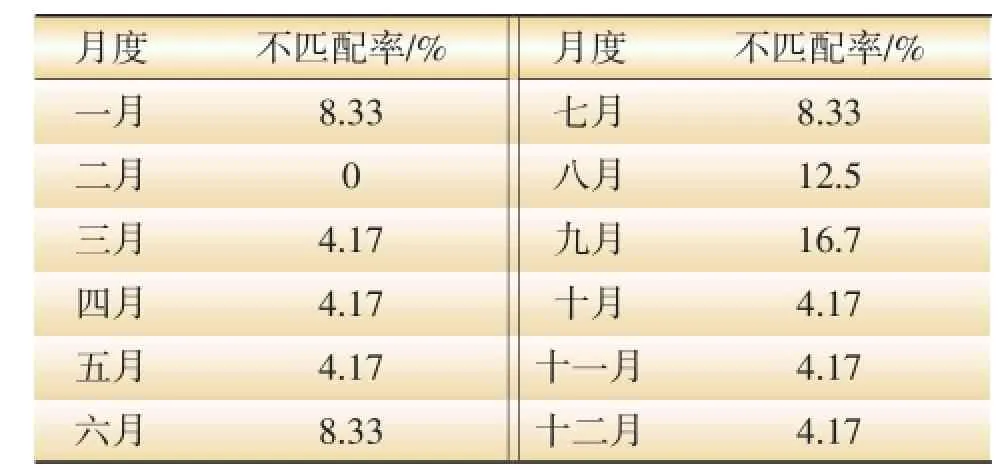
表3 最终按月度划分时段的不匹配情况

需要调整的是10：00～12：00、17：00～22：00共7个时段。时段调整后总电费变化率为2.635%，即峰谷电价时段调整后，短期内电网公司收取的电费会有所增加。这将会引导用户改变自身的用电行为，以响应峰谷时段的变化。峰谷时段重新划分后，对比图3中时段-负荷曲线与时段-电价曲线，可以发现两条曲线的切合度提高。

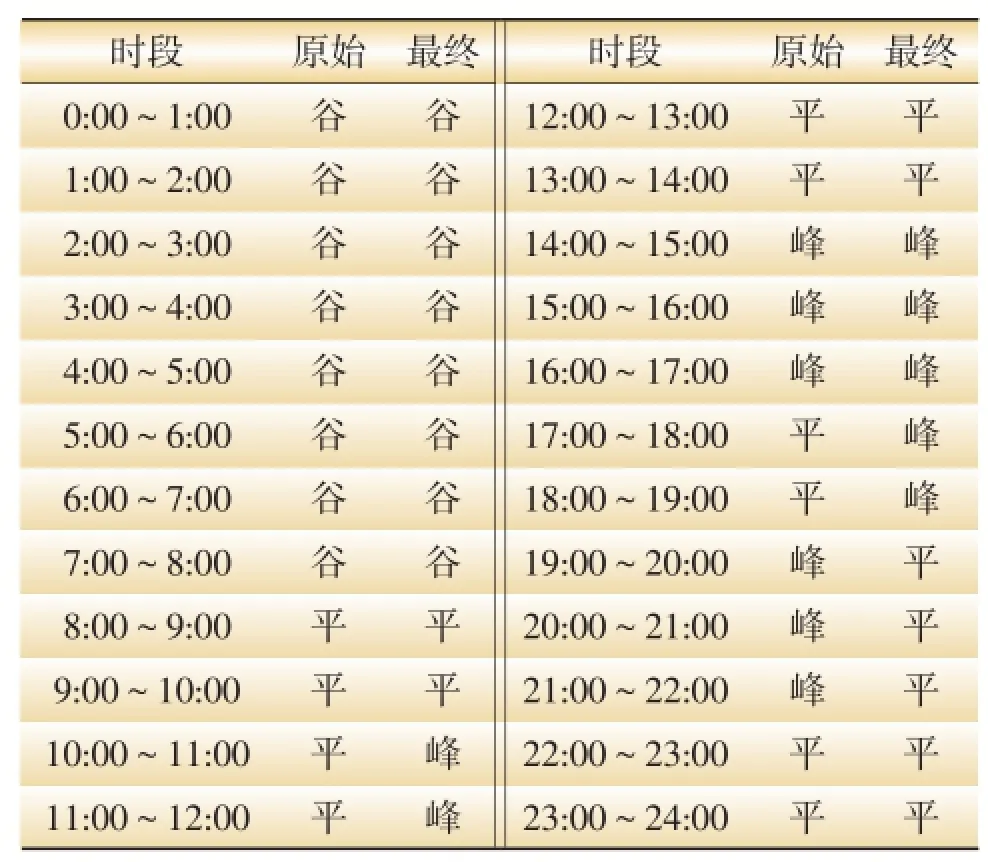
表4 2011全年最终的排序法时段划分表

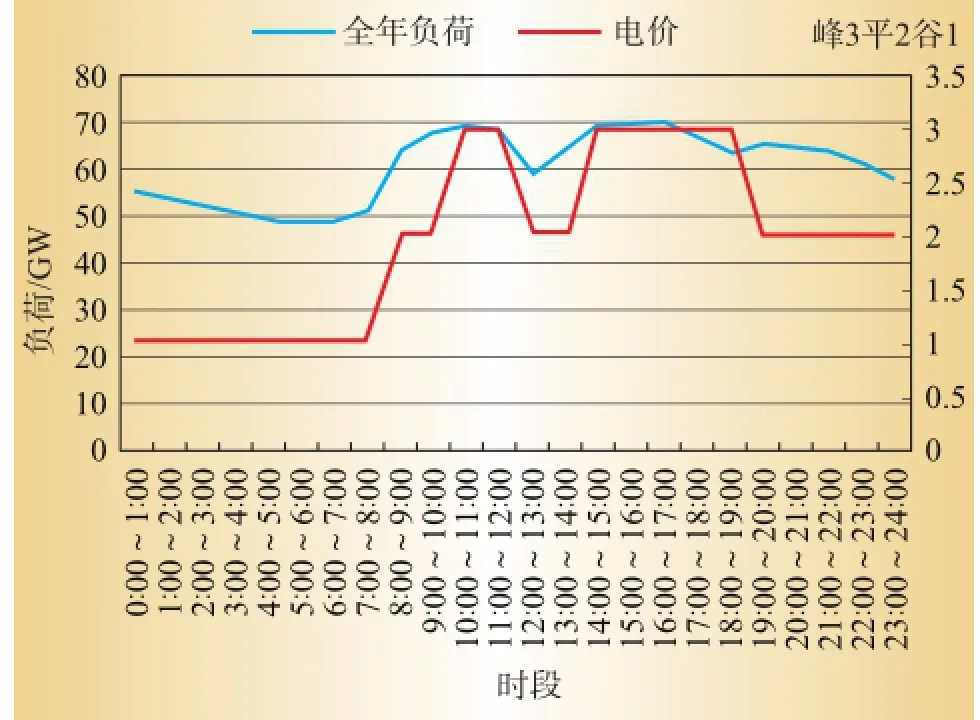
图3 2011年某省排序法的时段-负荷和时段-电价曲线

（2）K-means聚类分配法

抽象处理全年日负荷数据，得到与24个时段相对应的平均负荷值，用K-means聚类法将时段划分为峰平谷3类，结果如表5所示。

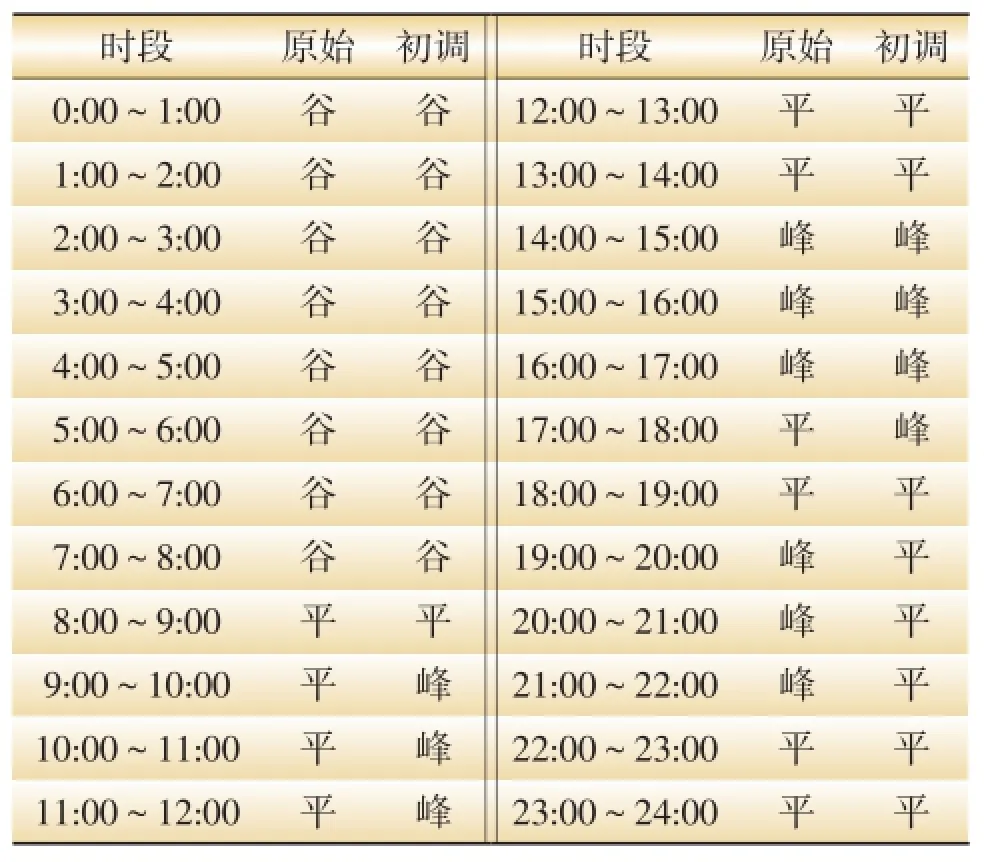
表5 2011全年初始的K-means法时段划分表

由表5可知，9：00～12：00，17：00～18：00，19：00～22：00这7个时段需要进行调整，其中若修改时段9：00～10：00，则会出现孤立时段8：00～9：00，2种再修正方案为：

方案1：将9：00～10：00时段的状态还原为平时段。

方案2：为孤立时段介绍友时段。根据孤立对象前后时段的峰谷分布及不匹配情况，将8：00～9：00时段变为峰时段。

因为用方案1和方案2对初始时段调整方案再修正后，全年的峰谷时段不匹配率均为4.17%，所以为细化方案效果，将周期缩短为月度重新划分时段。表6列举了按月度划分时段与按方案1修正后分配时段的不匹配率，月度总不匹配率为16.67%。

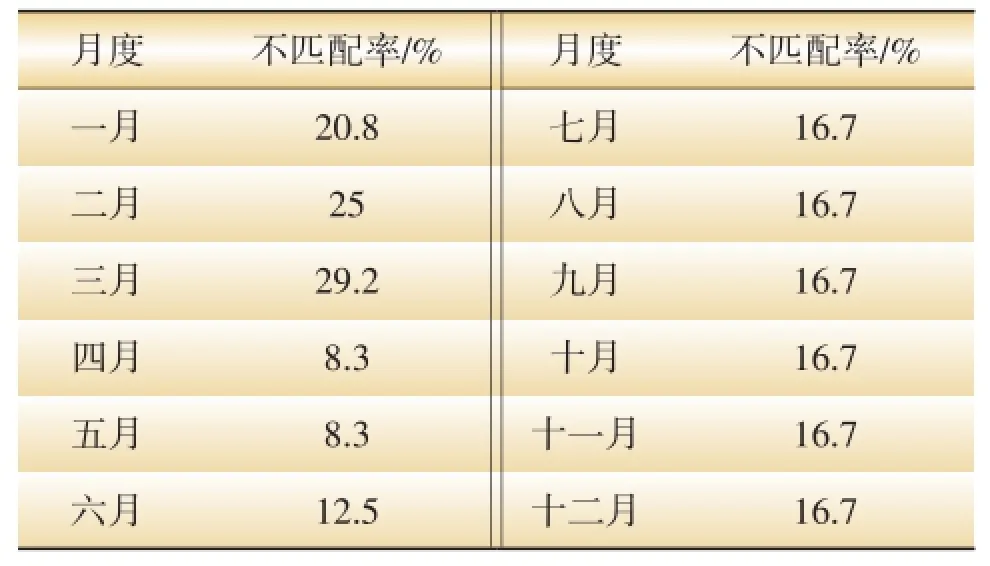
表6 方案1按月度划分时段的不匹配情况

由表6可知，方案1修正后的不匹配率很高，需辅以方案2进行修正。方案2中若将8：00～9：00改为峰时段，月度总不匹配率为15.97%，仍没有较大改善。

虽然以K-means法得出的峰谷时段划分结果的年度不匹配率很小，但是月度的不匹配率较大。可知，用K-means法能反映出不同月度用电变化，仅对年度进行时段的总体调整是不可取的。根据各月度时段不匹配情况，重新划分峰谷时段，得到结果如表7至表10所示。

按季节分别划分峰谷时段后，月度总不匹配率为5.90%，修正后峰谷时段的不匹配率大大降低，最终各月度的时段划分不匹配情况如表11所示。总电费变化率为3.306%，调整方案能够引导用户的用电行为。

K-means聚类法更加注重对数据潜在特性的类别划分，而不仅仅是排序分类。因此，K-means法更能体现出季节对用户用电行为的影响。

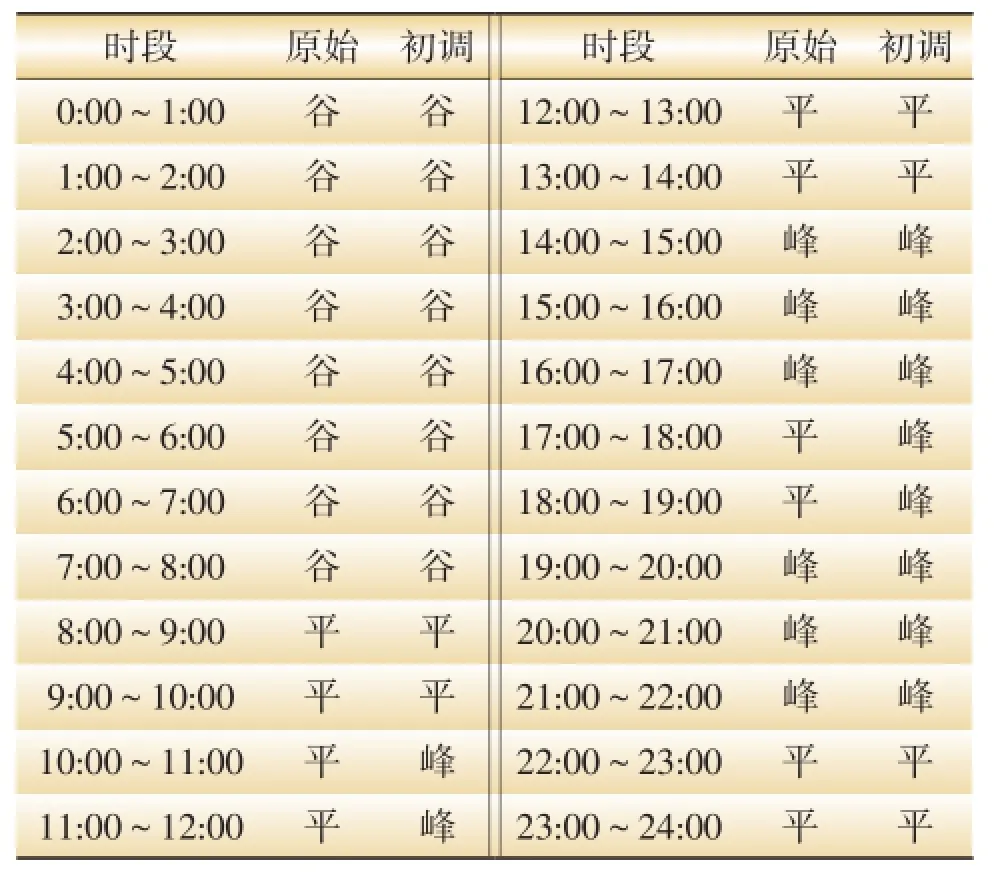
表7 2011年1—3月K-means法时段划分表

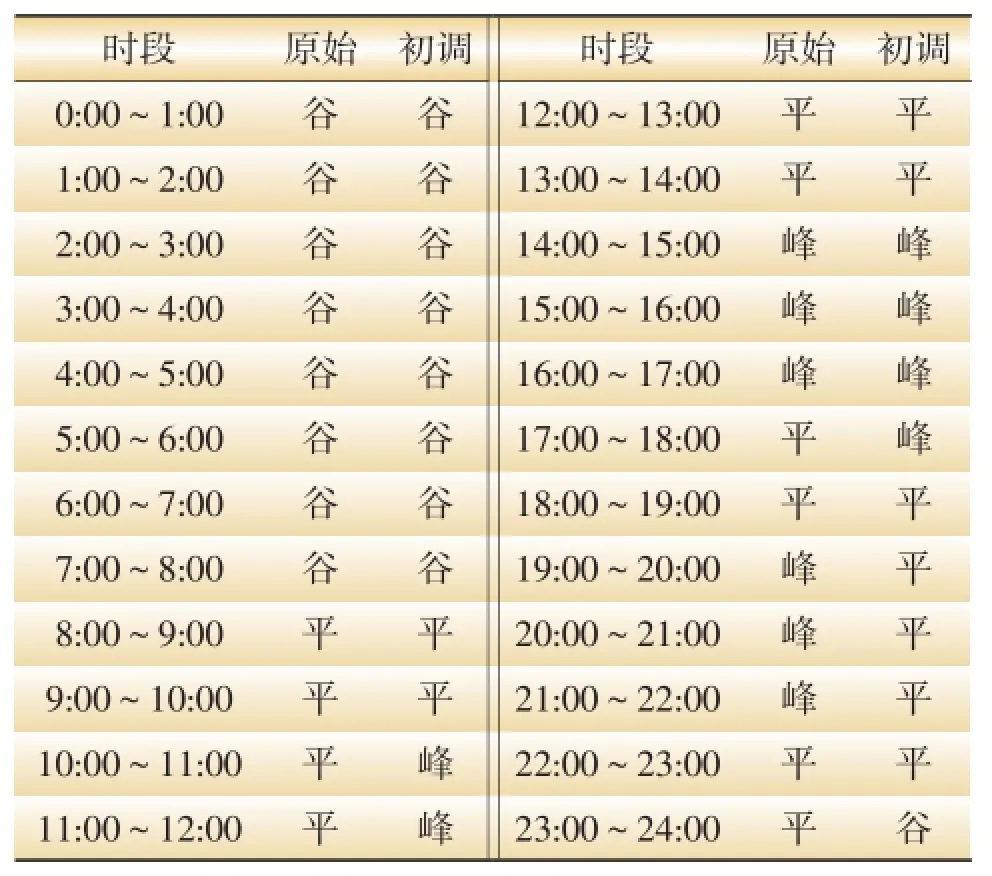
表8 2011年4月、5月K-means法时段划分表

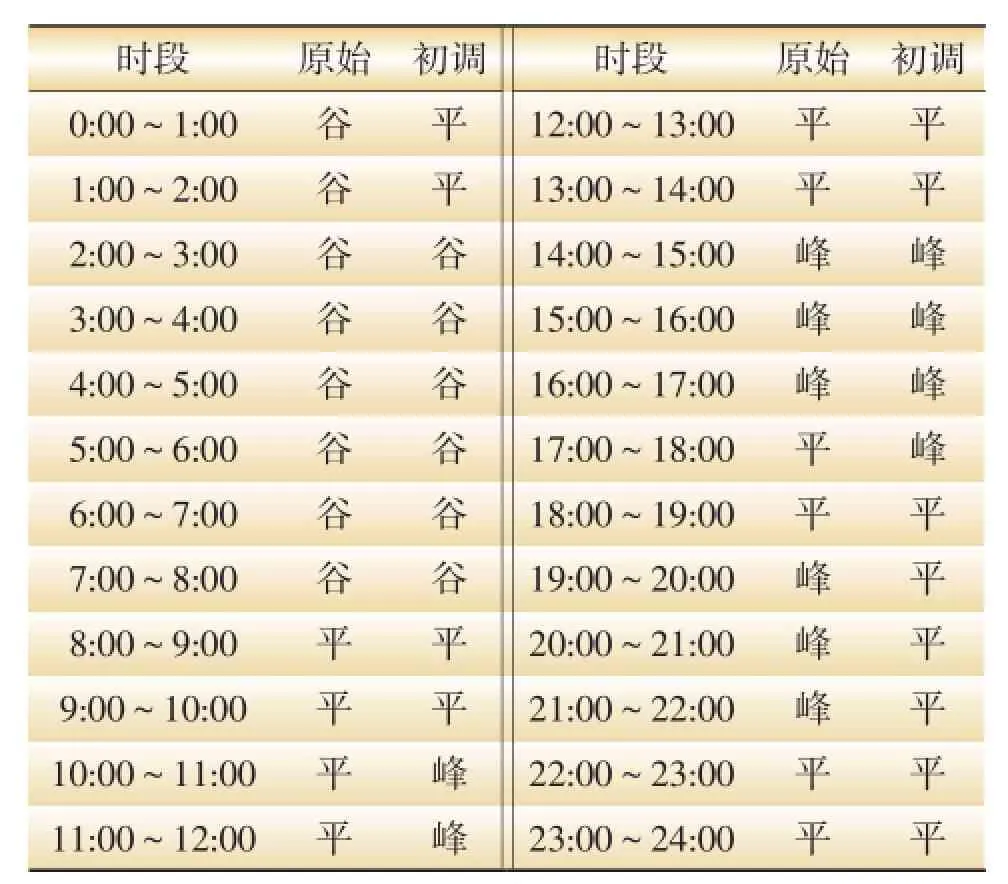
表9 2011年6—9月K-means法时段划分表

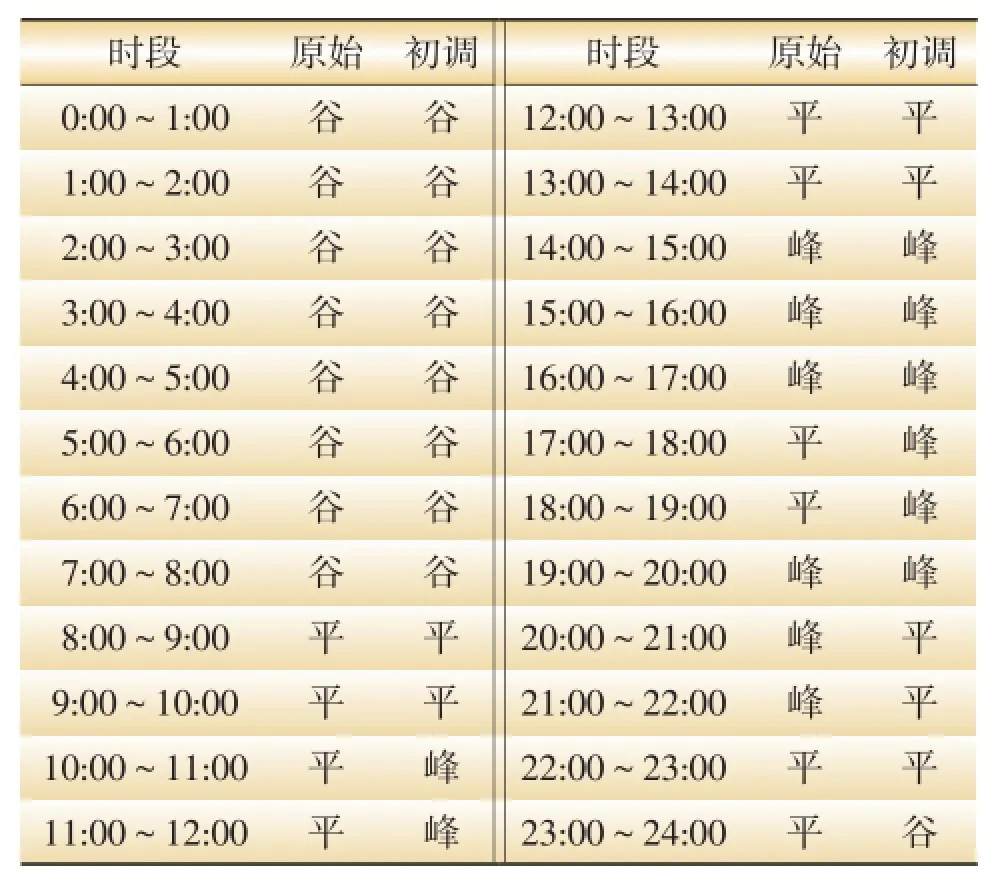
表10 2011年10—12月K-means法时段划分表

表11 最终按月度划分时段的不匹配情况

6 结束语

设置峰谷电价时段是需求侧响应的有效措施，时段的合理划分与调整对实施峰谷电价机制具有重要意义。本文就时段划分问题，提出了考虑需求侧响应的峰谷时段调整模型框架。本框架由三个模块构成，即基于负荷数据的时段划分模块、时段调整模块以及效果评估模块。时段划分模块运用了排序分配法和K-means聚类分配法划分时段，时段调整模块采用剔除或介绍友时段的方法处理孤立时段，效果评估模块结合设定指标，对比了这两种分配方法的优缺点，分析了时段调整的意义，发现K-means聚类法更能反映季节对用户用电行为的影响。最终得出结论：当时段-电价曲线与时段-负荷曲线切合度较高时，峰谷时段机制可以正确引导用户的用电行为，最终达到削峰填谷的目的，降低投资成本，提高机组利用率，促进需求响应的良性发展。相反，较低的曲线切合度会使供需问题变得更加严峻。最后必须提及的是本文在考虑电价时段时并未计及电价响应的效果，相应的需求响应体现在动态的电价调整机制中，这也是较为符合实际工程需要的一种做法。

［1］ 靳华伟，秦立军，陈茜，等.关于智能电网中需求侧响应技术的探讨［J］.中国电业（技术版），2011（7）：17-22.

［2］ 程瑜，翟娜娜.基于用户响应的分时电价时段划分［J］.电力系统自动化，2012，9（36）：42-47.

［3］ 林旻，朱艳卉，胡百林.基于供电成本的峰谷时段划分及分时电价研究［J］.华东电力，2005，33（12）：90-91.

［4］ 李震，洪添胜，曾祥业，等.基于K-means聚类的柑橘红蜘蛛图像目标识别［J］.农业工程学报，2012（23）：147-153.

［5］ 王千，王成，冯振元，等.K-means聚类算法研究综述［J］.电子设计工程，2012，20（7）：21-24.

［6］ 刘宝华.从需求侧管理到需求侧响应［J］.电力需求侧管理，2005，7（5）：10-13.

［7］ 黄韬，刘胜辉.基于K-means聚类算法的研究［J］.计算机技术与发展，2011，21（7）：54-62.

［8］ 黄震华，向阳.一种进行K-means聚类的有效方法［J］.模式识别与人工智能，2010，23（4）：516-523.

［9］ 邹云.实施峰谷电价的基本原则探析［J］.电力需求侧管理，2003，5（6）：13-15.

［10］ 全生明，卢键明.需求侧响应机制的国际经验及对我国的启示［J］.电力需求侧管理，2009，11（2）：73-76.

［11］ 王蓓蓓，李杨，高赐威.智能电网框架下的需求侧管理展望与思考［J］.电力系统自动化，2009，33（20）：18-22.

［12］ 唐捷，胡秀珍，任震，等.峰谷分时电价定价模型研究［J］.电力需求侧管理，2007，9（3）：12-16.

［13］ 谭东.广东省峰谷电价实施及大工业用户响应研究［J］.湖北电力，2003，27（5）：55-57.

［14］ 杨大雄，陈雁.上海市峰谷分时电价特性与效益分析［J］.华东电力，2005，33（11）：20-23.

［15］ 黄永浩，康重庆，李辉，等.用电需求曲线建模及其应用［J］.电工电能新技术，2004，23（1）：29-33.

［16］ 秦祯芳，岳顺民，余贻鑫.零售端电力市场中的电量电价弹性矩阵［J］.电力系统自动化，2004，28（5）：16-19.

Periods division method for peak-valley prices based on clustering algorithm

ZHAO Ming1，DONG Li2，LI Meng⁃yang1，GAO Ci⁃wei2，YU Jie2
（1.Electric Power Academy，Yunnan Electric Power Experiment Research Institute（Group）Co.Ltd.，Kunming 650000，China；2.School of Electrical Engineering，Southeast University，Nanjing 210096，China）

Reasonable periods division of peak-valley price can greatly improve load characteristics.Based on the customers' demand response，this dynamic adjustment model framework of peakvalley periods is established，which is composed by three modules of period division，adjustment and assessment.After preprocessing daily load data，all the periods are divided into three categories named as peak，normal and valley，with the use of sorting method and K-means clustering method.Considering the actual operating conditions，the method removes or introduces the friend periods to the isolated periods.After discussing the index changes to judge the implementation effect，the phenomenon shows that K-means clustering method can better reflect the impact of seasonal variation on the consumers'electricity consumption behavior.At last，this model is applied on the real data of some regions.The results demonstrate that when the period-price curve highly matches with the peak-valley periods，this model can effectively shift peak load，improve the efficiency of generator set and stimulate demand response through the adjustment of time period partition scheme.On the contrary，the load characteristic index will be worsened.

demand response；peak-valley price；period adjustment；sorting division；K-means clustering division

TM731

A

10.3969/j.issn.1009-1831.2016.04.003

2016-04-27；修回日期：2016-06-21

云南省电网公司科技项目（项目名称：基于用户能效特性的电网需响应关键技术研究）。江苏省青蓝工程资助。国家自然科学基金项目（51577029）国家高技术研究发展计划（国家863计划）项目（2015AA050401）

赵明（1964），男，云南大理人，教授级高工，硕士，研究方向为电网运行与调控技术；董力（1993），女，江苏扬州人，硕士研究生，研究方向为电力市场与电力需求响应；李孟阳（1987），男，云南个旧人，工程师，硕士，研究方向为电力系统通信及控制。