化折为直，巧解最值

程巨银

（六安市皋城中学，安徽 六安 237000）

化折为直，巧解最值

程巨银

（六安市皋城中学，安徽 六安 237000）

初中数学中，我们常会遇到这样的一类问题：“如何求解线段之和最小？”，此类问题出现形式多样，解题方法灵活多变，很多同学遇到后觉得比较困难，究其原因是我们找不到合适的切入口，导致思维受阻。下面笔者基于自己的教学实践，对问题进行分类梳理，谈谈如何巧用图形化折为直，妙解最值问题，希望对读者有一定帮助。

初中数学；巧用图形

一、两定一动

例1（1）如图1，已知直线l 的同侧有两个点A 、B，在直线l 上找一点P 使PA+PB最小，方法如下：作A（或者B）关于直线l的对称点A′（或B′），连接A′ B（或B′ A）与直线l的交点即为所求。

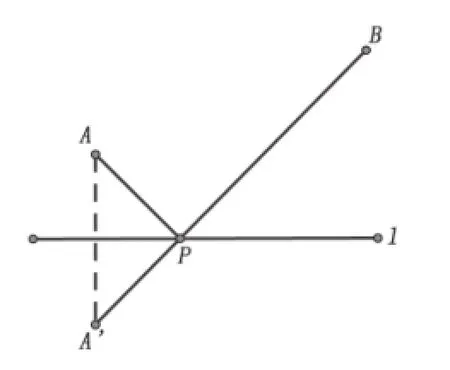
图1　

例1 （2）如图2，在等边∆ABC中，D为BC 中点，P为AC上任意一点，求PB+PD最小值。

注：例1属“两个定点+一个动点”类问题，且两个定点都在动点所在直线的同侧，解决此类问题时，常需利用图形的轴对称性，将其中一个定点进行轴对称变换（对称轴即为动点所在直线）到直线另一侧，由“两点之间线段最短”，连接对称点与另一点形成线段即为线段和的最小值。

二、两动一定

解析：可先假设N为一定点，将其转化为“两定一动”问题，即作C 关于BD 对称点C′，则C′在AB 上，连C′N交BD 于M ，由“两点之间线段最短”可知CM+MN最小值=C′M+MN=C′N 。

再考虑N 是BC上一个动点，C′为AB上一个定点，由“直线外一点与直线上各点的连线中，垂线段最短”，可知当C′N′⊥BC时，C′N′最小（如图4），即CM+MN最小，而∠C′ BN ′=45°，，∴C′N′=4

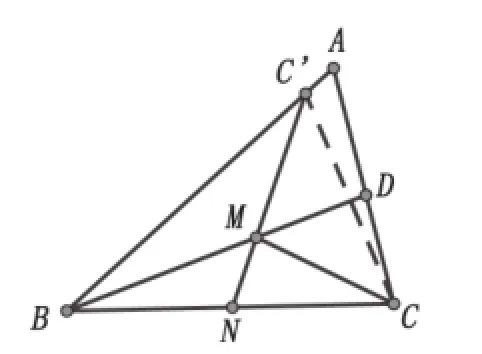
图3　

图4　

三、两定两动

解析：易求A（-3，1），B（-1，3）

作A 关于x 轴的对称点A′（-3，-1），作B 关于y轴的对称点B′（1，3），连A′ B′交x轴于P ，交y 轴于Q ，此时四边形PABQ的周长为：，即为周长最小值，故A′ B′两点确定的直线即为所求。

图6　

图7　

（2）如图7，在平面直角坐标系中，A（1，2），B（5，4），在x轴上有两点E 、F （E 点在F 点左侧），且EF=1，当四边形AEFB 周长最小时，求E点坐标。

注：本例均属“两个定点+两个动点”类问题。其中（1）是两动点中两轴上，分别作两个顶点关于两轴的对称点，由“两点之间线段最短”，将“折线段”转化为“直线段”。（2）中两动点，其中一个随另一个动，且两动点之间距离保持不变，解决此类问题常需要借助平移将相关线段移到适当位置，使分散的条件相对集中，将两个动点转为一个动点，则可将问题转化为“两定一动”来解决。

G632

A

1671-864X（2016）07-0106-01