考虑温度/功耗/热导之间相互作用的单循环迭代热分析算法

潘月斗,王嘉琪,唐　亮,骆祖莹

(1.北京科技大学自动化学院,北京 100083; 2.北京科技大学钢铁流程先进控制教育部重点实验室,北京 100083;3.北京师范大学信息科学与技术学院,北京 100875)



考虑温度/功耗/热导之间相互作用的单循环迭代热分析算法

潘月斗1,2,王嘉琪1,2,唐亮3,骆祖莹3

(1.北京科技大学自动化学院,北京 100083; 2.北京科技大学钢铁流程先进控制教育部重点实验室,北京 100083;3.北京师范大学信息科学与技术学院,北京 100875)

随着纳米工艺的不断改进,温度对漏电流功耗和热导的影响日益显著.考虑温度/功耗/热导相互作用的3D芯片热分析需要采用迭代方法对温度进行精确求解,即先用功耗密度向量和热导矩阵来求解温度向量,再用求解出来的温度向量来刷新功耗密度向量和热导矩阵.为了提高3D芯片热分析的效率,本文以一个设定温度值下的均匀热导矩阵作为预条件,先提出了一种双循环、内循环低迭代次数的高效求解算法TPG-FTCG.鉴于TPG-FTCG具有超快的内循环收敛速度,本文省去了TPG-FTCG算法的内循环部分,提出了一种单循环、低迭代次数的TPG求解算法TPG-Sli.基于GPU(Graphics Processing Unit)并行加速技术,本文编写并改进了TPG-Sli的GPU加速算法.实验数据表明：与采用经典高效的ICCG算法进行3D芯片热分析的TPG-ICCG算法相比,在足够小的误差范围内,TPG-Sli的GPU加速算法可以获得120倍的速度提升.

算法;热分析;快速傅里叶变换;GPU并行

1　引言

随着集成电路(Integrated Circuit,IC)纳米工艺的不断改进,3D芯片已成为事实,提高了IC集成度与功耗,但不可避免地带来了发热问题,过高的工作温度可能导致芯片无法正常工作、甚至损坏芯片.因此在芯片设计中要反复进行温度优化,研究精确高效的3D芯片热分析方法已成为了一个EDA(Electronic Design Automation)领域的研究热点.

在纳米IC热分析中,温度/功耗/热导参数之间存在着明显的相互影响.一方面随着衬底温度的升高,晶体管漏电流功耗显著增加,推高最终的芯片温度[1].另一方面随着温度的升高,硅材料的热导率会出现明显的下降,使得热阻升高,也会影响最终的温度分布[2].本文综合考虑了温度/功耗/热导(T/P/G)三方面相互影响的关系,对考虑T/P/G相互影响的TPG热分析方法及其快速求解算法进行了系统地研究.

为了综合考虑T/P/G之间的相互影响,TPG采用迭代求解方法逼近精确解，即先用功耗密度向量P和热导矩阵G来求解温度向量T,再用求出的T来刷新P和G.由于在迭代过程中热导矩阵G是变化的,尽管现有的不完全乔莱斯基分解共轭梯度算法ICCG[3]能够根据P和G来迭代求解T,如果采用ICCG进行TPG求解,就构成了内外双循环迭代求解算法TPG-ICCG,但其收敛速度较慢,每次求解T都需要很多次迭代,TPG-ICCG算法具有外循环迭代次数少和内循环迭代次数多的特点,过多的迭代次数降低了TPG的分析效率.

为了提高TPG的分析效率,本文采用FTCG算法[4](Precondition Conjugate-Gradient algorithm with the Fast Transform-based Preconditioner)来构建一种双循环、内循环低迭代次数的高效求解算法TPG-FTCG,该算法以一个设定温度值下的均匀热导矩阵GA作为预条件,每次求解T仅需要极少次数的迭代.鉴于TPG-FTCG具有超快的内循环收敛速度,本文直接省去其内循环,提出了一种单循环、低迭代次数的高效TPG求解算法TPG-Sli (Single-loop iterative),该算法先以GA为预条件、采用双重快速傅里叶变换(FFT)的共轭梯度方法直接根据P和G求解出含微量残差的T,再用这个含微量残差的T来刷新P和G,最后收敛于一个具有较高精度的求解结果.基于GPU并行计算技术,本文编写了GPU并行算法TPG-Sli-GPU,并利用系数矩阵预存储技术编写其优化算法TPG-Sli-iGPU.

2　相关工作与本文贡献

在芯片设计的各种阶段都需要精度与速度各异的热分析算法来针对芯片温度进行设计优化,目前热分析算法包括：结构级热分析[4,13]、全芯片三维热分析[5～7]、统计热分析[8]等算法.全芯片三维热分析又分为稳态与瞬态热分析两种[5～7],其中稳态热分析是其它热分析的研究基础,一直得到广泛的研究,以适应不同应用的需求[8,13～15].

全芯片三维稳态热分析一般会对散热系统进行离散化以获得热导矩阵G,然后根据输入的功耗密度向量P,通过求解热分析方程GT=P,来获取芯片的温度分布向量T[5,6].目前采用逐次逼近的迭代方法进行求解的热分析算法主要有ICCG[3]、格林函数算法[9，10]、变向隐含算法(Alternating Direction Implicit,ADI)[7]、连续过松弛算法(Successive Over Relaxation,SOR)[8,15]、多层网格算法(Multigrid,MG)[6,14]等.其中ICCG是具有强鲁棒性的经典算法,被广泛地用做热分析算法研究的对比算法.对于迭代算法而言,只要能够降低其迭代的次数就能够降低其算法复杂度、提高其算法效率.

在热分析中,一般都假设芯片具有绝热四壁[7],如果假设与器件层平行的X-Y平面内的导热介质具有同质导热性能,那么芯片进行均匀离散化后,就可以采用基于FFT变换的热分析算法FT[4,11,12]进行直接求解,由于不需要迭代,FT算法具有高效的求解效率[11].对于X-Y平面具有非同质导热性能的应用,可以基于同质结构来构造一个预条件导热矩阵GA,采用预条件共轭梯度算法(PCG)或残差补偿方法进行迭代求解,如果GA越近似于实际热导矩阵G,则热分析需要的迭代次数就越少,热分析的求解效率就越高[4].

随着纳米工艺的不断改进,已有热分析研究不仅考虑温度升高对漏电流功耗的影响[1,8],也开始考虑温度升高对硅衬底热导的影响[2].由于在热分析中考虑T对G影响的研究才起步,目前还没有看到关于TPG热分析的研究成果.

与现有热分析算法研究相比,本文工作的贡献体现在如下方面：

(1)基于文献[4,12]所给出的FTCG算法,本文提出了TPG-FTCG算法,先以环境温度下的热导矩阵GA作为G的预条件矩阵,便于FT算法进行快速的预条件求解.与平均需要410次迭代才能求解出T的TPG-ICCG算法相比,TPG-FTCG算法平均只需要4～5次迭代就能够求解出T,在可以忽略的误差范围内,TPG-FTCG可以获得20倍左右的加速.

(2)为了进一步提高分析效率,本文提出了一种全新的单循环、高效TPG求解算法TPG-Sli.由于省却了内循环,TPG-Sli算法求解效率比TPG-FTCG提高了3倍.

(3)本文编写了GPU加速算法TPG-Sli-GPU和改进算法TPG-Sli-iGPU算法.在足够小的误差范围内,TPG-Sli-iGPU算法求解效率比TPG-FTCG提高了6倍,比TPG-ICCG提高了120倍.

3　研究基础

3.13D集成芯片的全芯片三维热分析模型

如图1所示,3D集成芯片主要对多个硅器件层进行垂直堆叠,3D芯片上下分别接着主散热通道和辅散热通道,鉴于主散热通道的散热能力是辅散热通道的20多倍,本文在3D芯片热分析中,忽略了辅散热通道、只考虑主散热通道.

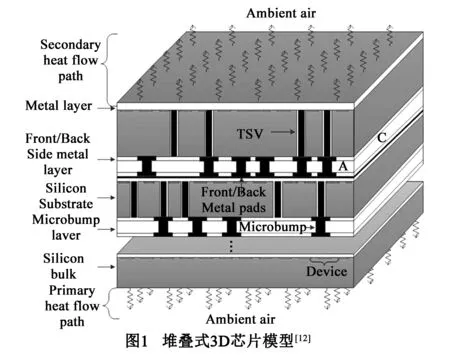
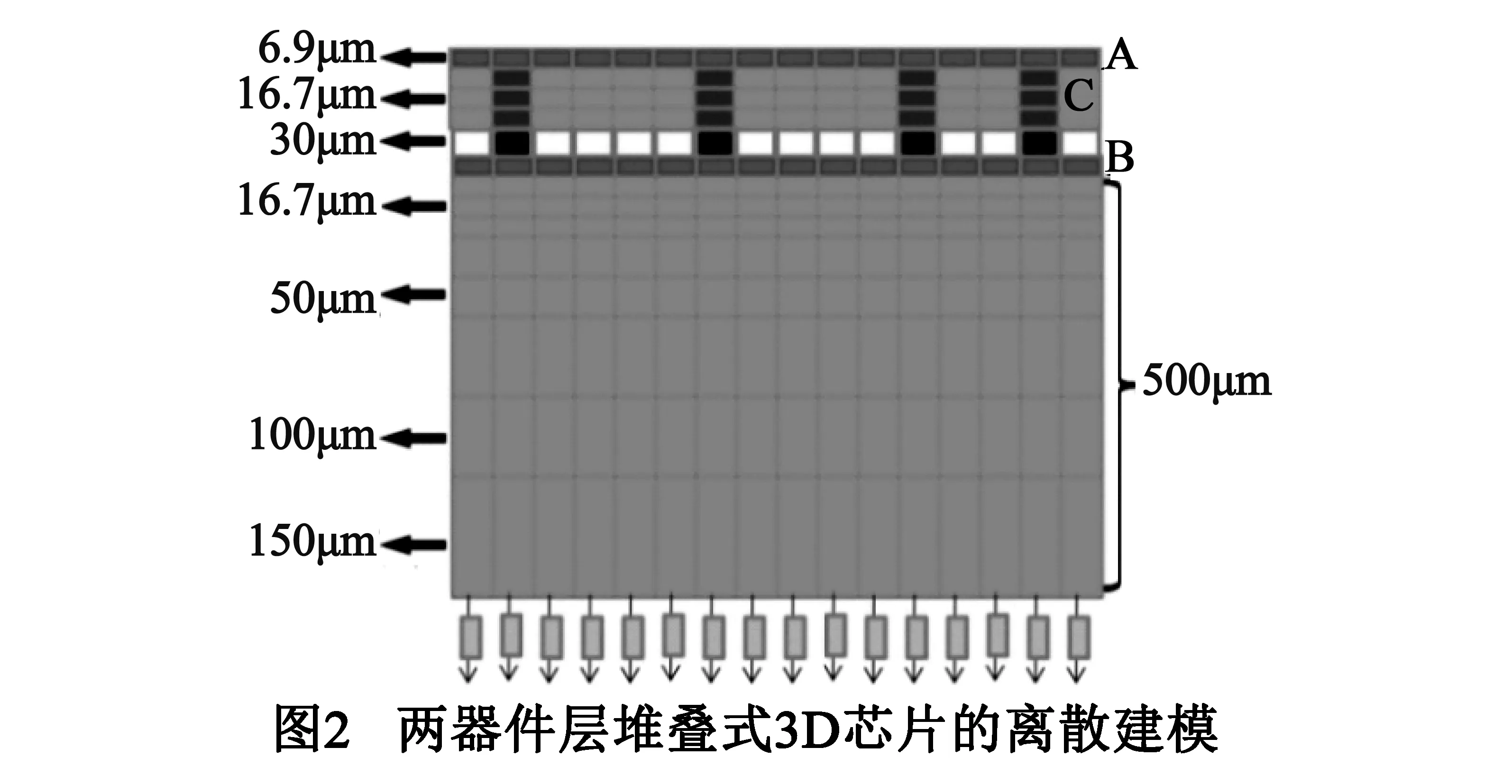
如图2所示,本文首先要对3D芯片内核进行离散化[12],将内核等分为nx(x轴)×ny(y轴)×nz(z轴)个长方体质元,并将每个质元等效为一个节点,即每个质元所产生的热量都被加到它的中心点,并将中心点温度作为质元温度.本文采用不同灰度的模块来表示不同材料质元：(1)灰度较浅的块为硅衬底离散后的硅质元,本文采用16.7μm厚度将剪薄硅衬底离散为3层,依次采用16.7μm/50μm/100μm/150μm厚度将常规厚度(500μm)硅衬底层离散为8层；(2)图2中A和B块为金属互连层的质元,本文金属互连层的铜材料占比设为50%,3D芯片功耗分布在互连层,其中附着于常规衬底的互连层功耗占总功耗的4/5,附着于剪薄衬底的互连层占总功耗的1/5；(3)图1中的A和C部分是粘接层的微压焊块质元与绝缘材料质元,其中微压焊块层厚度为30μm,微压焊块质元直径为30μm,均匀排列,微压焊块热导率为60W/(m·K),绝缘材料热导率为0.83W/(m·K);(4)图2中C块为TSV质元,TSV直径为6μm,TSV的热导率为406W/(m·K),均匀排列在微压焊块质元下方.

3D芯片离散化后，采用下式进行稳态热分析：

GT=P

(1)

式中,T与P分别是节点温度分布向量与功耗密度分布向量,G为热导矩阵.

3.2温度与功耗的相互影响

随着芯片工作温度T的提高,导致芯片漏电流Ilk显著地增高[1],二者的函数关系如下式所示：

Ilk(T)=Ilk(V0,T0)(AT2eαVdd+β/T+BeγVdd+δ)

(2)

式中,V、T分别是电压与温度向量,且V0、T0为它们的初始向量.Ilk(V0,T0)初始的漏电流向量,A、B、α、β、γ和δ是不同芯片规模下的经验常数[1].根据式(1)和式(2)可以看出,温度升高导致功耗增加,而功耗增加又会反过来会推高温度.

3.3温度与热导的相互影响

文献[2]详细地说明了温度与硅材料热导率在热分析中的相互作用.当温度从300K升到400K时,根据下式给出的温度与硅材料热导率之间的二次拟合函数，硅的热导率将下降32%左右.

k(T)=0.0018*T2-0.7575*T+166.5162

(3)

即温度T和热导G在热分析中同样存在一个正反馈关系.根据式(1)～(3)可以看出,温度升高导致硅热导率下降,反过来会推高温度与功耗.

3.4温度、功耗、热导之间的相互影响

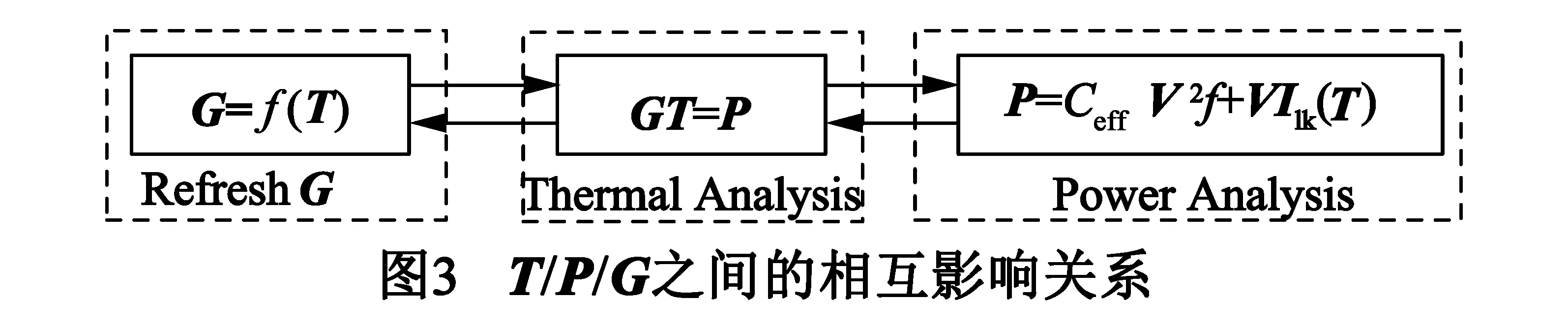
如图3中框所示,热分析中热导矩阵G和功耗密度向量P决定了节点温度向量T,反映了热导和功耗对于温度的影响.如图3左框所示,根据节点温度向量T来计算热导矩阵G,以反映温度对热导的影响.如图3右框所示,根据节点温度向量T来计算功耗密度向量P,以反映温度对于功耗的影响.因此,T/P/G之间存在着直接的相互影响关系.

4　TPG热分析方法及其高效算法

4.1考虑温度/功耗/热导之间相互影响的热分析方法TPG及其算法流程

在初始温度条件下,TPG首先利用初始的功耗密度向量P0和热导矩阵G0计算温度向量T0；然后根据T分别刷新P和G,从而计算出更为精确的T.就这样TPG方法采用迭代的方法不断产生新的T直到收敛于T的准确解,最后通过对P进行累加获取精确的芯片功耗Pchip.图4给出了TPG方法的算法流程图,TPG算法包含以下算法步骤.

Step 1先输入室温Ta=45℃下的G0和T0、P0；再将G0/T0/P0赋值给G/T/P.

Step 2求解GT=P以获得温度向量T.

Step 3判断任意节点i的温度变化量|δTi|是否小于给定误差限ε1=1e-2,如果是,则停止迭代跳到Step 5.

Step 4根据温度向量T刷新热导矩阵G和功耗密度向量P,返回Step 2进行下一轮的迭代.

Step 5输出精确的温度向量T和芯片功耗Pchip.

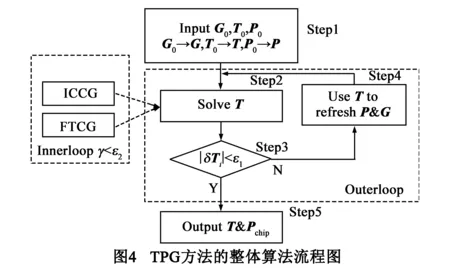
由于在Step 4中根据T刷新G和P的复杂度很小,而Step2求解GT=P的算法复杂度则很大,所以选用高效率算法来求解T决定了TPG热分析的效率.鉴于热导矩阵G是非均匀变化的,无法使用FT算法来直接求解GT=P,必须采用迭代算法来精确求解T,以构成具有内外两个循环迭代求解的TPG热分析算法.

如果采用ICCG算法来求解Step 2 GT=P,就构成了TPG-ICCG热分析算法.如表1所示,对一个具有14M节点的测例,当ICCG的迭代判出残差限设为ε2=1e-6时,尽管外循环的迭代次数仅有13次就能够收敛,但由于内循环的迭代次数非常多,进行一次TPG分析所需要迭代总数达到5336次,平均内循环的迭代次数为410次,这表明ICCG收敛速度太慢,难以为大规模热分析提供满意的求解效率.

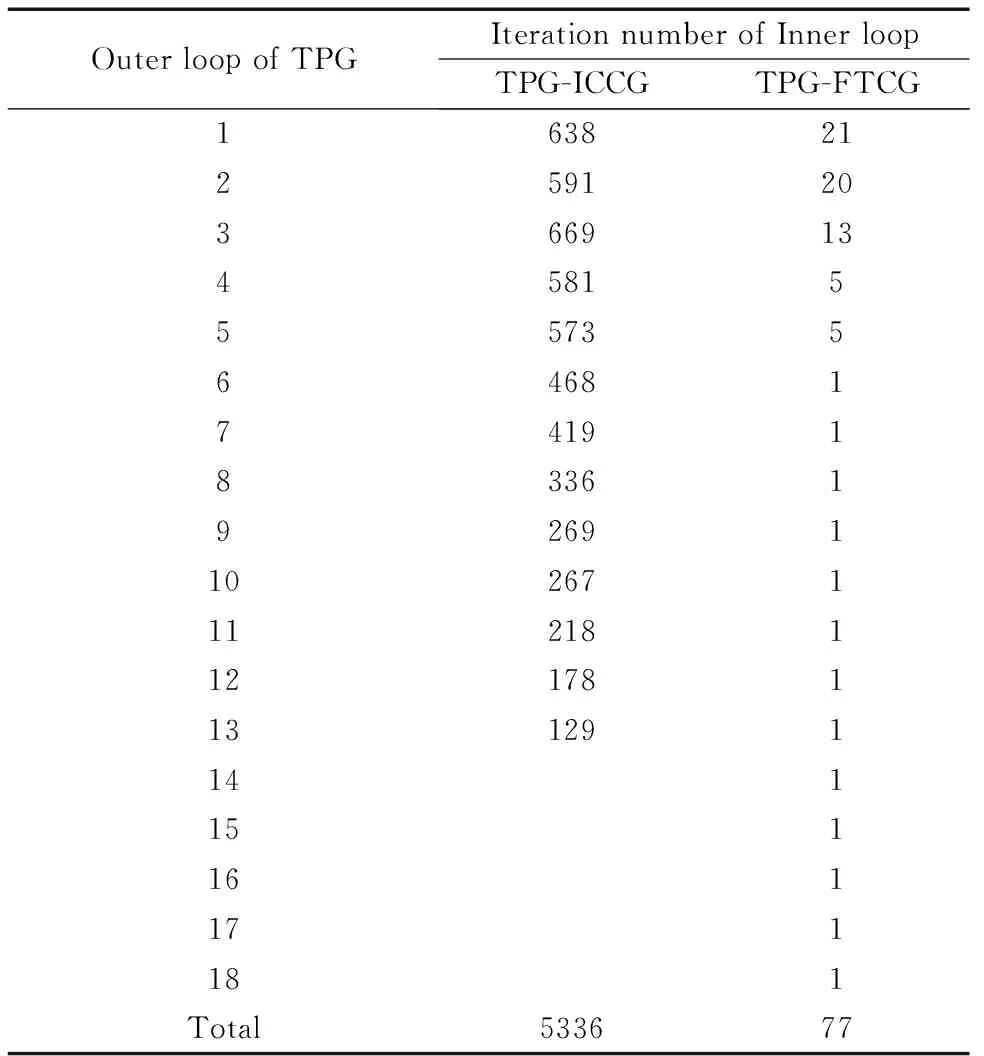
表1　TPG-ICCG、TPG-FTCG的收敛次数对比

4.2基于快速傅里叶变换进行预条件求解的共轭梯度算法TPG-FTCG

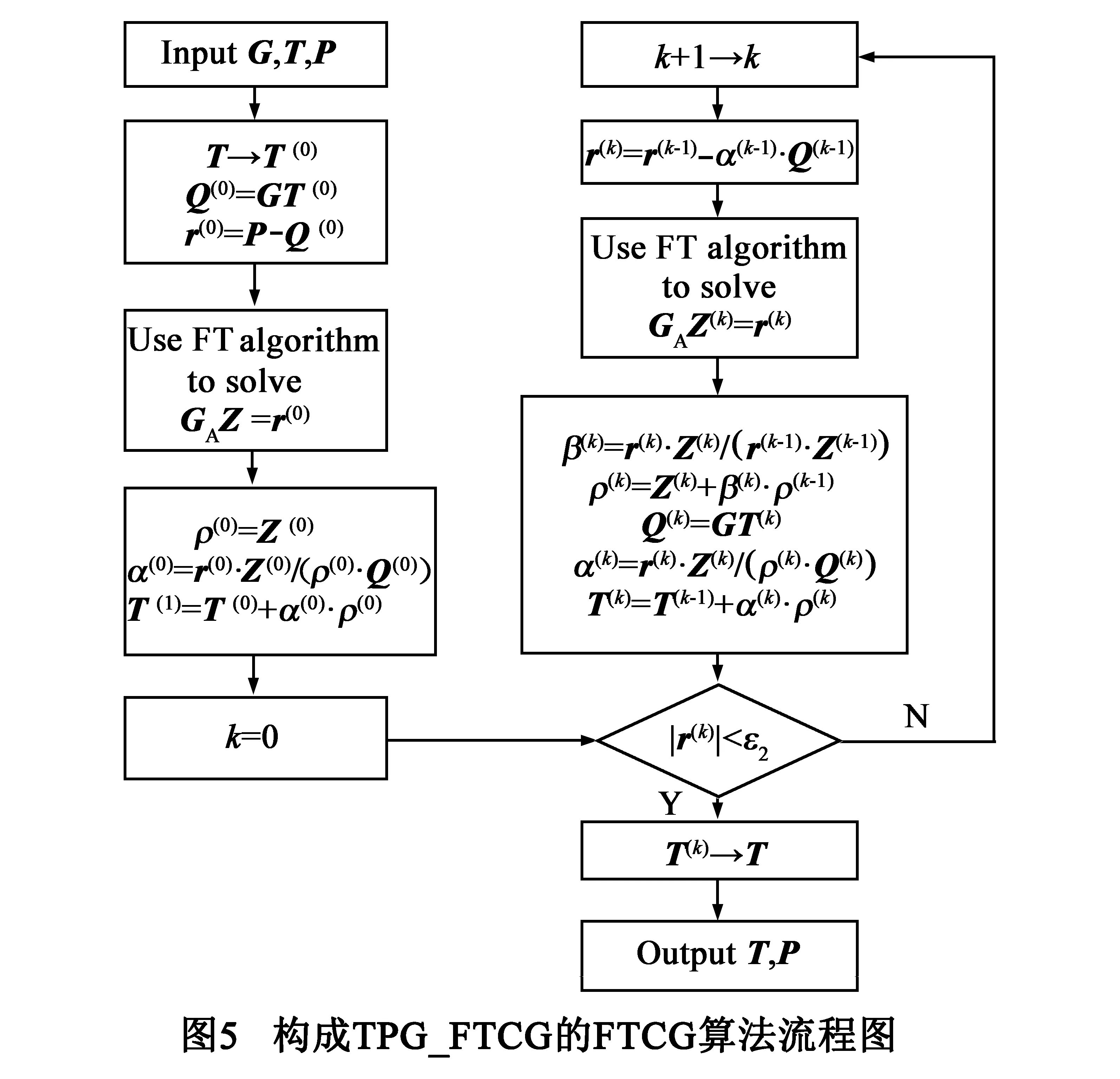
为了提高TPG热分析的求解效率,在图4中本文将FTCG算法[3]引入TPG热分析中,构建了TPG-FTCG算法.如图5所示,FTCG算法能够以较高的收敛速度对GT=P进行求解.

3D芯片存在非同质热导问题,无法直接用室温Ta=45℃的热导矩阵来构建满足FT算法直接求解的热导矩阵GA,下面TSV质元为例,说明如何构建满足要求的GA.在图6中,将TSV质元中心点温度设为节点温度,需要获取该质元六个方向的热导才能计算出其中心点温度.两个相邻质元的热导可以看作是两质元中心点到边界面热导值的串联,即

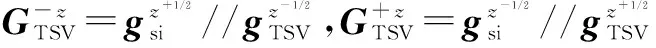
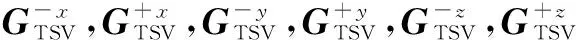
文献[14]规定：参与FT算法的预条件矩阵值不能小于原矩阵最大值的50%,本文选取每层最大的热导值(无论是水平热导还是垂直热导)的93%作为预条件的矩阵热导值.以图6为例,该TSV所在硅衬底层的预条件矩阵水平方向热导值即为

垂直方向热导值即为

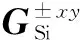
对于进行热传导的硅材料而言,当工作温度从45℃升高到90℃时,其热导率从136.0199下降到113.1025,即下降了16.85%,这表明：对于一个最高工作温度小于90℃的芯片,相对于室温Ta下的预条件矩阵GA,实际热导矩阵G的热导变化小于16.85%,远小于文献[12]设定的50%限制.对于FTCG算法而言,GA越接近于G,则其收敛的速度越快,如表1所示,本文FTCG算法除了前5次迭代中需要521次迭代以外,剩余迭代仅需要1次就可以将迭代残差降到设定值10-6之下,具有很好的收敛特性.

4.3改进的单循环算法TPG-Sli

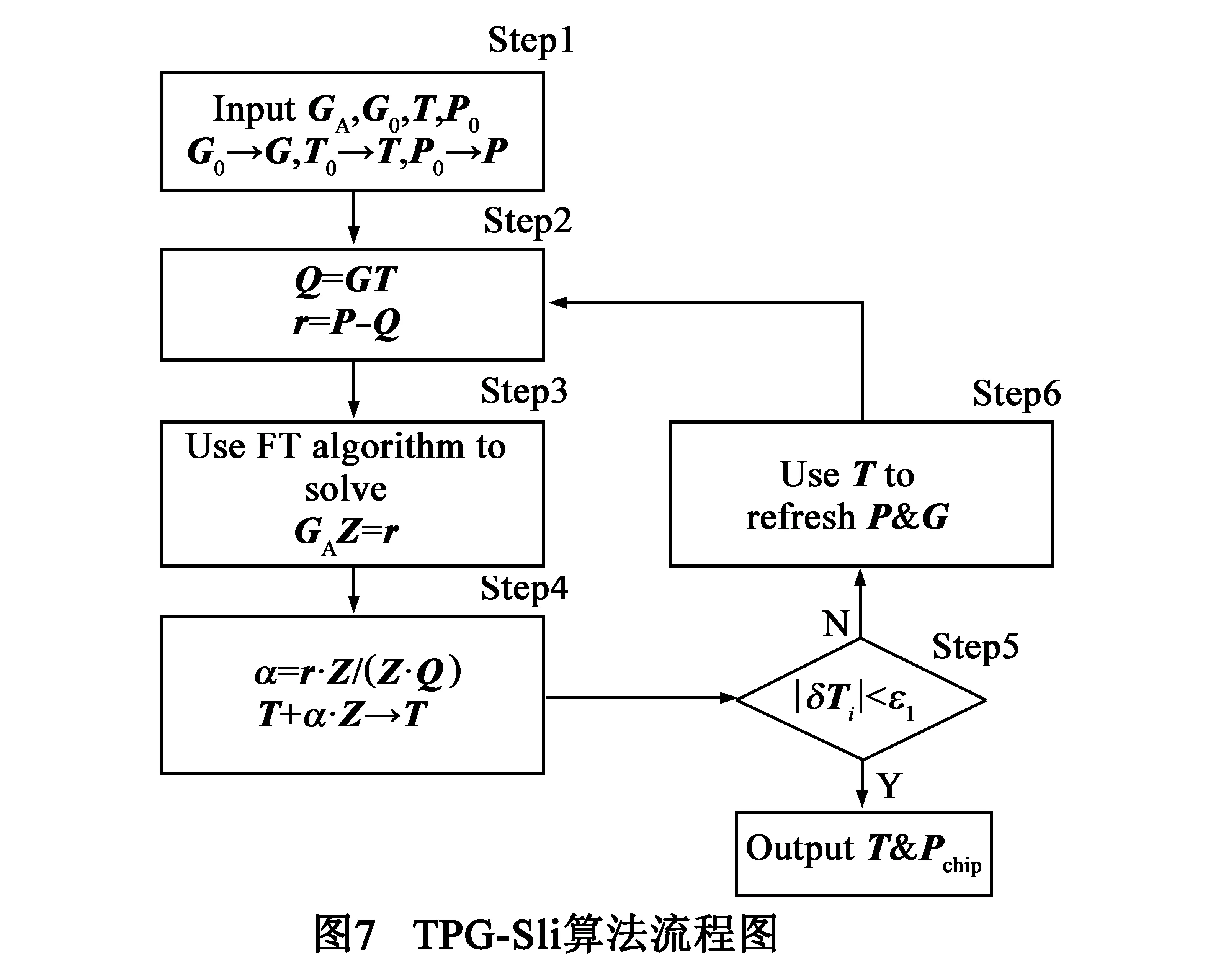
根据TPG-FTCG算法残差收敛速度极快的特点,本文进一步删除了图6中FTCG算法的循环体部分,仅使用FT算法进行一次T的预条件共轭梯度求解,提出了单循环的改进算法TPG-Sli,以进一步降低TPG热分析算法的时间复杂度.

如图7所示,TPG-Sli算法是一个单循环的迭代算法,每次迭代不是直接求解T,而是先根据残差向量r=P|Q=P|GT,再使用FT算法直接求解GAZ=r以获得补偿向量Z,接着计算共轭梯度方向,最后沿着共轭梯度方向对T进行修正,即T=T+αZ.与TPG-FTCG算法相比,TPG-Sli算法尽管速度有所提高,但每次求出的T含有较大的误差,导致最终的热分析精度有所下降.

4.4TPG-Sli的GPU并行加速及其优化

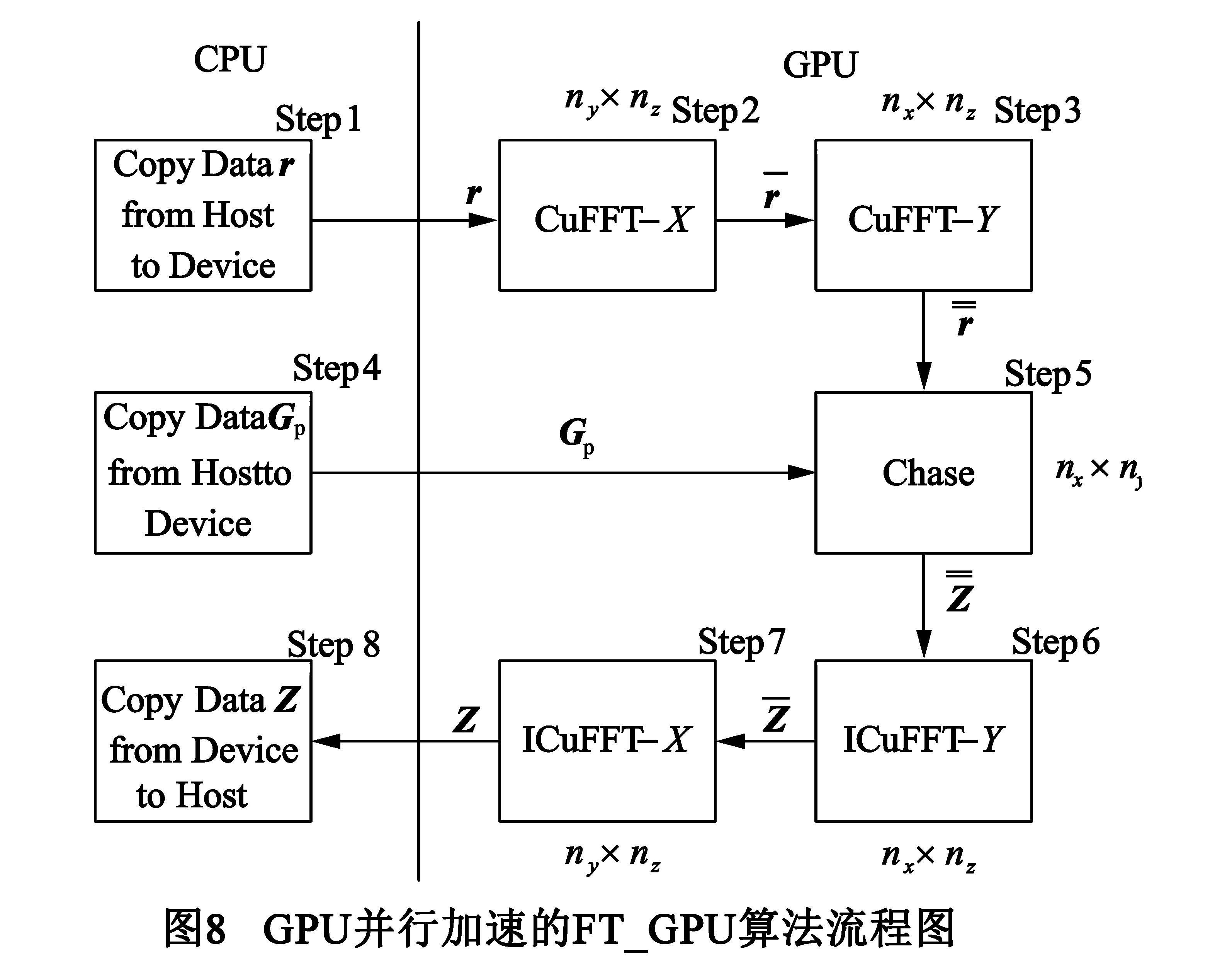
下面结合具体的算法步骤对FT-GPU进行算法并行性分析：

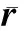
从以上的并行计算分析可以看出：与已有FT算法[4]仅简单地调用Cu-FFT库函数进行GPU加速相比,本文FT-GPU算法的并行计算全部在GPU端完成,仅需要和CPU进行3次数据传输,分别在Step1和Step4将r和Gp从CPU端拷入GPU端,在Step8将Z从GPU端拷回CPU端,可以大量减少数据传输时间.

TPG-Sli需要多次调用FT算法进行预条件的求解,将FT算法升级为GPU加速的FT-GPU算法后,TPG-Sli就升级为其GPU加速版本TPG-Sli-GPU.由于预条件矩阵GA是不变的,所以对它进行LU分解所获得的两对角矩阵Gp也是固定的,TPG-Sli-GPU多次调用FT-GPU算法,在Step4多次将Gp从CPU端拷贝至GPU端,需要耗费大量的数据传输时间.鉴于Gp是一个两对角矩阵,仅包含少于2N个非零元素N=nx×ny×nz,我们可以将Gp直接预存到GPU端,以节约数据传输时间,本文将这种改进的FT-GPU算法称为FT-iGPU,而将调用FT-iGPU算法的TPG-Sli称为TPG-Sli-iGPU.

5　实验结果

本次实验采用的是Visual Studio 2010中的C/C++语言实现算法,所有实验均运行于3.20GHz主频的Intel®Core(TM)i7-3930kCPU,内存容量为32GB,显卡为NVIDIA GTX 680,显存容量为4GB.

所有实验都采用了3种不同的芯片功耗分布进行对比验证,为了保证测例的典型性与普适性,本文只在测例1中采用均匀的功耗分布,测例2和测例3分别采用了AMD四核phenom架构和Intel四核nehalem架构的功耗分布.3D芯片共有两个器件层,即附着于剪薄硅衬底的互连层、3层含TSV的剪薄硅衬底层与微压焊块层、附着于常规衬底的互连层、8层常规厚度硅衬底共14层,每层共有1001×1001个节点,所以本测例的求解规模是14M个节点.三个测例的芯片总功耗均设为100W,其中附着于常规衬底的器件层产生了80W功耗.

5.1算法的精度对比

TPG-ICCG和TPG-FTCG算法都具有内外两个循环,TPG-Sli作为单循环的TPG分析算法,只具有外循环、而无内循环.以上3种算法的判出条件为节点温度的改进量|δTi|<ε1=10-2,TPG-ICCG和TPG-FTCG的内循环判出条件为残差|r|<ε2=10-6.为了评估算法精度,本文将采用残差限为ε2=10-16的TPG-ICCG求解结果作为比较基准(golden),来比较以上3种算法在最大温度Tmax、平均温度Tave以及芯片功耗Pchip三个参数上的分析误差.如表2示,3种方法计算出的Tmax、Tave以及Pchip几乎相同,绝对误差均在10-2左右,相对误差均小于0.1%,这表明以上3种算法都是精确的TPG热分析算法.

5.2算法的时间复杂度对比

采用三个测例对文中涉及的TPG-ICCG、TPG-FTCG、TPG-Sli-CPU、TPG-Sli-GPU、TPG-Sli-iGPU的算法运行时间进行比较,其运行时间依次标为T1～T5.如表2示,本文使用Ti-1/Ti来分析采用单项加速技术所带来的改进效果,使用T1/Ti来表示：相较于TPG-ICCG算法的运行时间T1,本文提出的4种改进算法所带来的总体加速效果.通过对表3中数据的分析,可以得出如下结论：

(1)对于TPG-FTCG,由于其内循环迭代次数较TPG-ICCG算法大大的减少,其求解速度是TPG-ICCG的16倍左右.

(2)与TPG-FTCG相比,TPG-Sli-CPU不含内循环,只用一个外循环进行TPG求解,因此可以有效降低算法的时间复杂度,其求解速度是TPG-FTCG的3倍左右,是TPG-ICCG的56倍左右.

(3)与TPG-Sli-CPU相比,TPG-Sli-GPU通过GPU并行加速来大幅度降低算法的运行时间,它的求解速度是TPG-Sli-CPU的2倍左右,是TPG-ICCG的90倍.

(4)与TPG-Sli-GPU相比,由于将两对角矩阵Gp预存在显存中,可以减少CPU端与GPU端的数据通信时间,使得TPG-Sli-iGPU在时间复杂度上又有了进一步的降低.因此,其求解速度是TPG-Sli-GPU的1.2倍,是TPG-ICCG的120倍左右.

(5)如上所示,本文先后采用了4种加速技术成功地将TPG热分析效率提高了120倍,获得了满意的加速效果,表明为了最大限度地提高热分析的效率,必须从算法设计和计算平台这两方面对TPG算法进行改进.

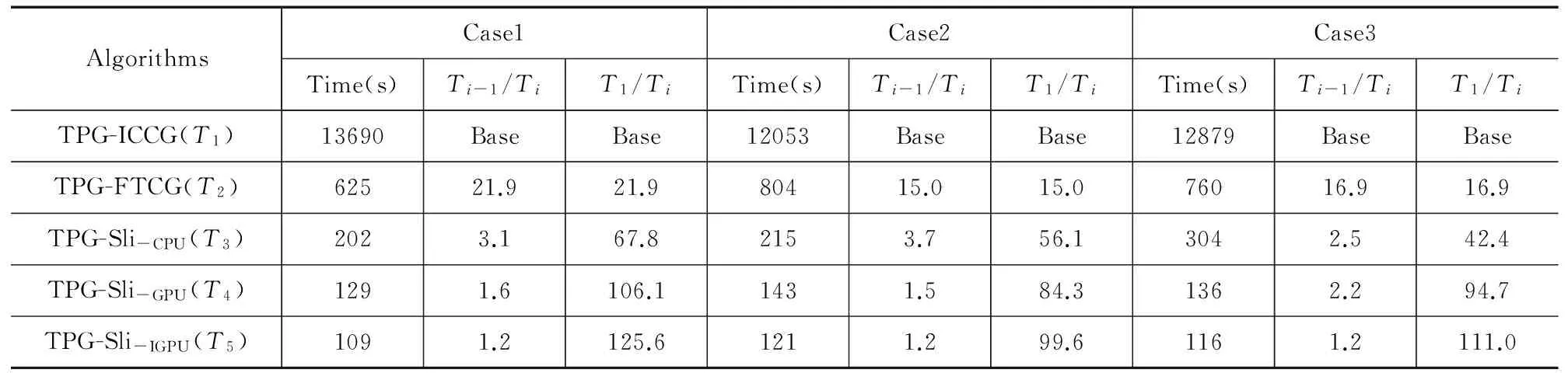
表2　不同算法的时间复杂度比

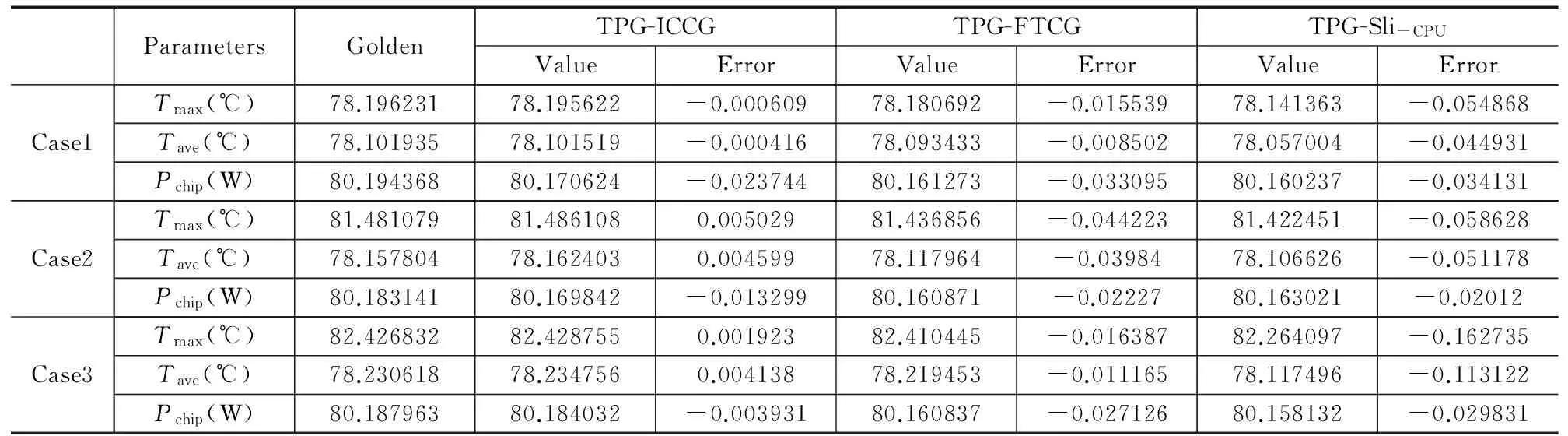
表3　算法的精确度对比

6　结论

本文对考虑T/P/G之间相互影响的TPG热分析方法进行了系统地研究.为了寻找TPG高效的求解算法,提出了一种基于快速傅里叶变换为预条件的高效双循环算法TPG-FTCG及其改进的单循环算法TPG-Sli,并且编写了TPG-Sli算法GPU并行加速版本TPG-Sli-GPU算法及其改进算法TPG-Sli-iGPU.实验结果表明,TPG-Sli-iGPU算法不仅可以快速地进行TPG热分析,能够对3D芯片进行精确而高效的热分析.

[1]Liao W P,et al.Temperature and supply voltage aware performance and power modeling at microarchitecture level[J].IEEE Transactions on CAD,2005,24(7):1042-1053.

[2]Liu Z,Tan S X D,et al.Compact nonlinear thermal modeling of packaged integrated systems[A].Proceedings of ASP-DAC[C].Yokohama:IEEE,2013.157-162.

[3]Wu X H,et al.Area minimization of power distribution network using efficient nonlinear programming techniques[J].IEEE Transactions on CAD,2004,23(7):1086-1094.

[4]Daloukas K,et al.A parallel fast transform-based preconditioning approach for electrical-thermal co-simulation of power delivery networks[A].Automation & Test in Europe Conference & Exhibition[C].Grenoble:IEEE,2013.1689-1694.

[5]Zhan Y,Goplen B,et al.Electro-thermal analysis and optimization techniques for nano-scale integrated circuits[A].Proceedings of ASP-DAC[C].Yokohama:IEEE,2006.219-222.

[6]Li P,Pileggi L T,et al.IC thermal simulation and modeling via efficientmultigrid-based approaches[J].IEEE Transactions on CAD,2006,25(9):319-326.

[7]Wang T Y,Lee Y M,et al.3D thermal-ADI—an efficient chip-level transient thermal simulator[A].Proceedings of ISPD[C].Monteray:IEEE,2003.10-17.

[8]Luo Z Y,Tan S X D,et al.Localized statistical 3D thermal analysis considering electro-thermal coupling[A].Proceedings of ISCAS[C].Taibei:IEEE,2009.1289-1292.

[9]Zhan Y,Sapatnekar S S.High efficiency Green function-based thermal simulation algorithms[J].IEEE Transactions on CAD,2007,26(9):1661-1675.

[10]Oh D K,Chen C P,et al.3DFFT:Thermal analysis of non-homogeneous IC using 3D FFT Green function method[A].Proceedings of ISQED[C].San Jose:IEEE,2007.567-573.

[11]Qian H F,Sapatnekar S S,et al.Fast poisson solvers for thermal analysis[A].Computer-Aided Design[C].Monterey:IEEE,2010.698-702.

[12]Lee Y M,Wu T H,et al.A hybrid numerical and analytical thermal simulator for 3-D ICs[A].Proceedings of DATE[C].Grenoble:IEEE,2013.1379-1384.

[13]Yan J Q,Luo Z Y,et al.Accurate architecture-level thermal analysis methods for MPSoC with consideration for leakage power dependence on temperature[A].Proceedings of ISQED[C].Santa Clara:IEEE,2013.178-183.

[14]Feng Z,Li P.Fast thermal analysis on GPU for 3D-ICs with integrated microchannel cooling[A].Proceedings of ICCAD[C].San Jose:IEEE,2010.551-555.

[15]Huang K,Yang X,et al.Efficient electro-thermal co-analysis on CPU+GPU heterogeneous architecture[A].Proceedings of ISQED[C].Santa Clara:IEEE,2012.364-369.

[16]Chen J,Wu X J,Cai R.Parallel processing for accelerated mean shift algorithm with GPU[J].Journal of Computer-Aided Design & Computer Graphics,2010,03:461-466.

潘月斗男，1966年出生，博士，副教授.主要从事交流电动机智能控制理论，研究及高速高精交流电动机驱动系统的计算机数字控制系统设计.

E-mail:ydpan@ustb.edu.cn

王嘉琪男，1989年出生，硕士研究生.主要从事电热综合分析、高性能并行计算方面的研究工作.

E-mail:3706157@qq.com

TPG-Sli:Single-Loop Iterative Thermal Analysis Algorithm Considering Interactions Among Temperature,Power and Heat Conductance

PAN Yue-dou1,2,WANG Jia-qi1,2,TANG Liang3,LUO Zu-ying3

(1.SchoolofAutomation,UniversityofScienceandTechnologyBeijing,Beijing100083,China;2.KeyLaboratoryofAdvancedControlofIronandSteelProcess(MinistryofEducation),Beijing100083,China;3.CollegeofInformationScienceandTechnology,BeijingNormalUniversity,Beijing100875，China)

With the improvement of the nanometer technology,the influences among temperature,leakage power and heat conductance become increasingly significant and it should be taken into account in 3D chip comprehensive thermal analysis to solve the accurate temperature based on the iterative solution.The comprehensive thermal analysis method uses the nodal power density vector and the heat conductance matrix to solve the nodal temperature vector,and then,refreshes power density and heat conductance with the obtained nodal temperature.In order to improve the efficiency of 3D chip comprehensive thermal analysis,this work uses the heat conductance matrix as the precondition under a setting temperature.Then it proposes an efficient algorithm TPG-FTCG(CG with the Fast Transform-based Preconditioner) which has double-loop and lower inner-loop iterations.According to TPG-FTCG’s fast inner-loop convergence rate,this work removes TPG-FTCG’s inner-loop part then proposes a more efficient TPG solving algorithm TPG-Sli(Single-loop iterative),which only has single-loop iterative and fewer iterations.Based on the GPU parallel computing,this work compiles and refines TPG-Sli’s GPU-parallel-computing algorithm.Experimental results demonstrate that:On the premise of precision losing,the TPG-Sli’s GPU algorithm can achieve about 120X speedup compared with the TPG-ICCG algorithm,which uses the classical and efficient ICCG to deal with the 3D chip comprehensive thermal analysis.

algorithm;thermal analysis;Fast Fourier transform;GPU parallel computing

2014-07-22;修回日期:2015-06-25;责任编辑：梅志强

国家自然科学基金(No.51331002)

TP393

A

0372-2112 (2016)06-1300-07