一种基于PFRFT的低截获信号识别算法*

张柏林　熊智威　吴宏超

(空军航空大学　长春　130022)



一种基于PFRFT的低截获信号识别算法*

张柏林熊智威吴宏超

(空军航空大学长春130022)

摘要针对低截获概率雷达信号的调制识别问题,提出了一种新的调制类型识别算法,完成了LFM、BPSK、2FSK、Frank/P1/P2/P3/P4码8种低截获信号的识别分类。首先,根据有无调频斜率,利用PFRFT完成低截获信号的预分类。然后,综合利用分数阶域主副脊线及功率谱估计完成信号的自动分类识别,给出了分类识别算法的流程图及具体步骤。最后通过仿真实验,表明该算法具有很好的识别效果,证明了该方法的有效性和可行性。

关键词PFRFT; 脉内调制; 功率谱估计; 低截获信号

Class NumberTN911.7

1　引言

随着现代电子技术的发展,降低雷达信号被侦察截获的可能,提高雷达的战场生存能力,成为雷达发展趋势,越来越多的低截获概率雷达开始涌现在战场,并开始占据主体地位。低截获概率雷达采用复杂波形设计来降低雷达的可检测性和可识别性,使截获接收机面临严峻挑战,研究雷达信号脉内调制类型识别技术,对于提高电子战能力具有重大意义。目前针对低截获雷达信号调制类型识别的方法主要有时频图像法[1～2]、多重相位差分法[3～4]、基于功率谱估计的识别方法[5]、基于高阶累积量的识别方法[6],以上算法计算量普遍较大,提取的特征不明显,且对于多相码信号的识别分类效果差,不利于自动化识别分类的实现。

针对现有算法的优缺点并结合低截获雷达信号脉内调制特点,提出了一种新的基于PFRFT的低截获信号调制类型识别算法,该算法首先根据有无调频斜率将信号分为两类,然后再利用脊线数目、相位差分和AR模型功率谱估计完成信号的进一步识别分类。该方法简单有效地解决了多相码信号的识别分类难题,具有较高的识别准确率,且易于工程化实现。

2　脉内信号调制模型

低截获雷达信号的脉内调制类型种类繁多,根据调制要素大致可分为两类:频率调制和相位调制。其信号模型可以统一表示为

s(t)=a(t)exp(j2πft+φ(t)+θ0)

(1)

其中,a(t)是低截获信号的幅度函数,f为载频,φ(t)为调制函数,θ0为初始相位。低截获信号的调制类型取决于调制函数φ(t)[7～8],调制类型的识别主要是针对φ(t)进行识别。

本文主要针几种对常用的低截获雷达信号调制类型的识别问题进行研究,包括线性调频信号(LFM)、频率编码信号(2FSK)、二相编码信号(BPSK)和多相编码信号(Frank码、P1码、P2码、P3码、P4码)。

3　基于PFRFT的低截获信号识别算法

3.1PFRFT基本原理及性质

虽然FRFT可以对单个周期的LFM实现最佳的能量聚集[9～12],但是当处理采用连续波体制的LPI信号时处理效果却不理想,会将信号当作多个信号分量进行处理,因此不是最优处理算法,针对这一问题,黄宇、刘峰等提出了PFRFT算法来对连续波LFM信号进行分析。为了实现对信号的完全匹配,将FRFT的核函数进行修改,加上信号的周期调制特性,并考虑截获信号时延的影响,得到对于信号f(t)的PFRFT定义如下

(2)

其中Kp,τ,T(u,t)为

Kp,τ,T(u,t)=

(3)

其中,mod()是取余函数,PFRFT与FRFT的关系为

(4)

(5)

由上式可知PFRFT可以看作是对信号f(t)以周期T和时延τ进行截取后在各自周期内进行FRFT,然后进行累加而得。因此与FRFT具有类似的性质。图1给出了2周期的LFM信号的分别利用FRFT及PFRFT得到的分析结果。

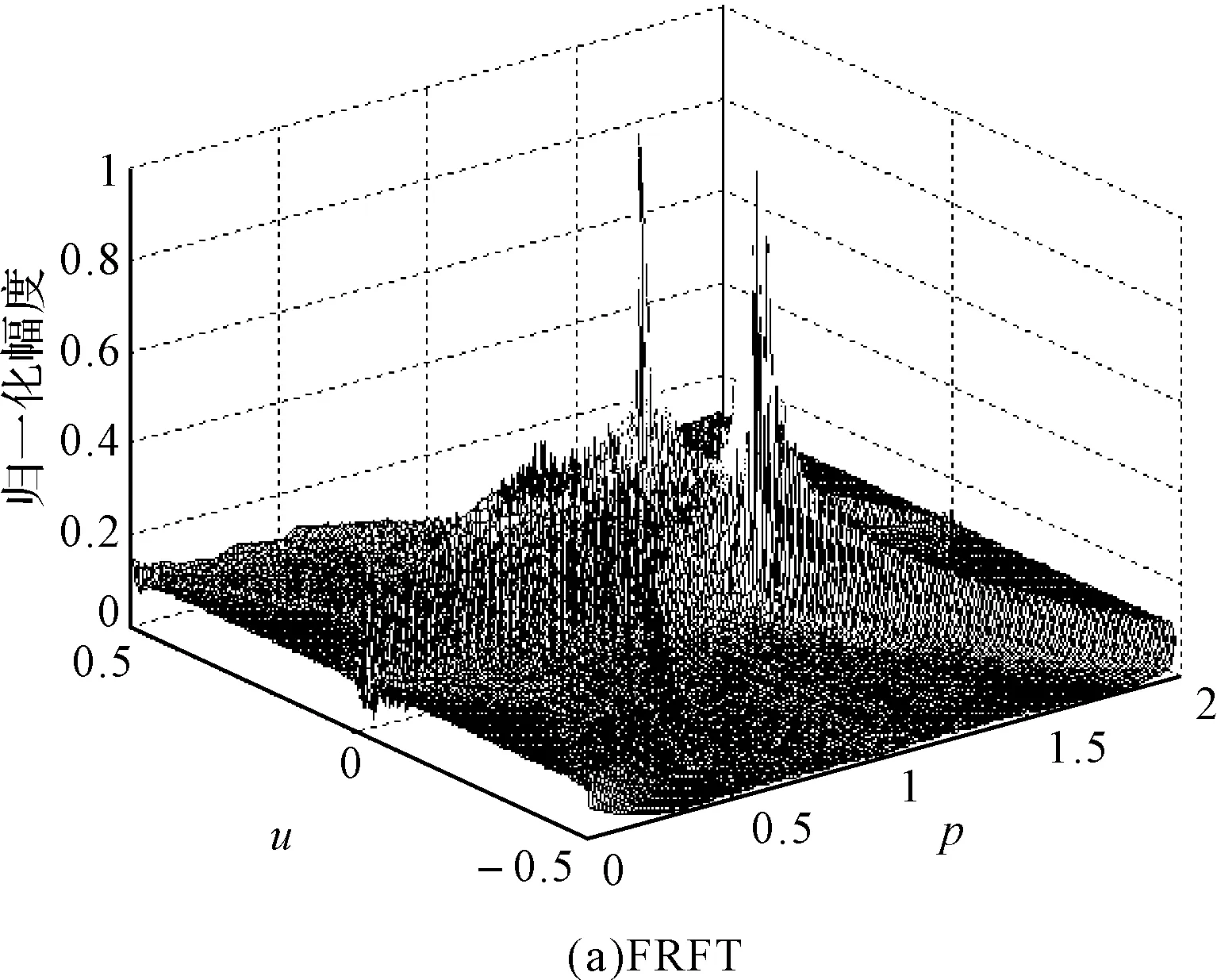
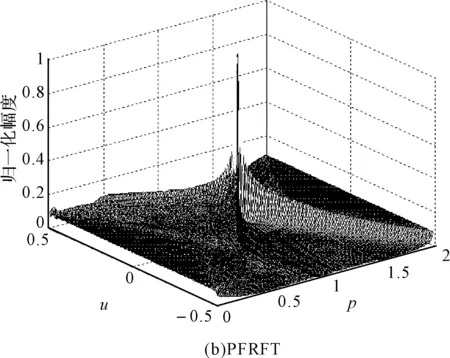
图1　利用FRFT及PFRFT对2周期的LFM信号的分析结果

由图1可知当截获处理的信号不为单周期时利用FRFT变换会对信号进行处理时会出现多个峰值,会对信号识别产生严重的干扰,而对于PFRFT而言由于核函数加入了周期调制特性,当截获到多个周期的信号时,只有当信号周期与核函数周期匹配时形成独立的唯一峰值,而当截获信号为单个周期时PFRFT的处理效果与FRFT相同,因此利用PFRFT对LPI信号进行分析更为合适。

3.2基于调频斜率的预分类

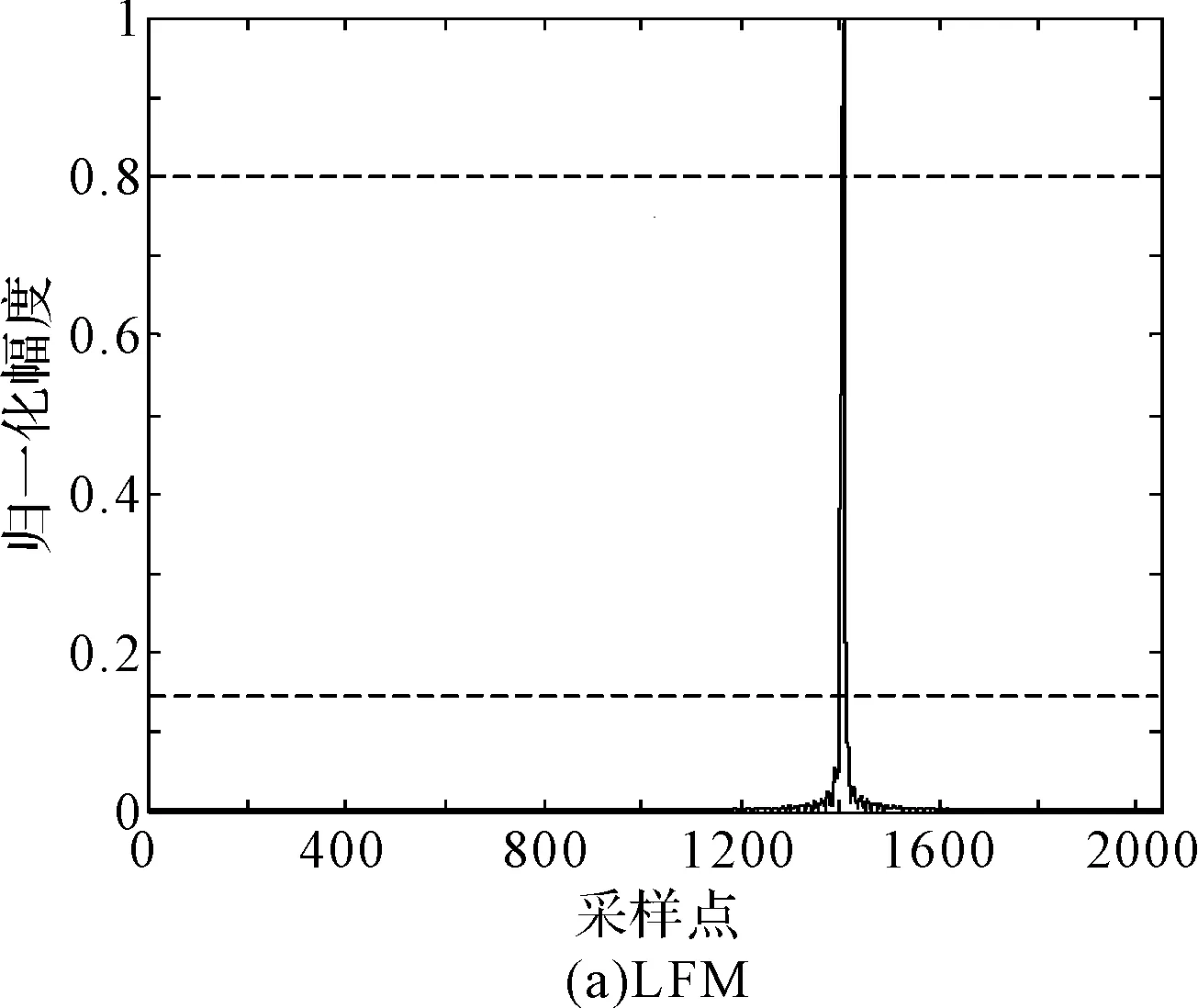
上一节分析可知PFRFT的检测结果可以得到信号的调频斜率及周期信息,而由于噪声信号不具有调频及周期特征,故不能产生峰值效应,所以PFRFT具有较好的抗噪性能,由此得到较为精准的调频斜率信息。由第二章及第三章的分析可知Frank码等多相码及LFM信号的所对应的调频斜率不为0,而BPSK、2FSK信号不具有线性调频特征即调频率为0。根据信号的这一特征可以利用PAHT变换来完成信号的预分类,通过预分类可以得到两类不同性质的信号:第一类信号的调频斜率为0,第二类信号的调频斜率不为0。图2给出了这8种信号的PAHT在对应周期下的调频斜率与幅度的关系图。

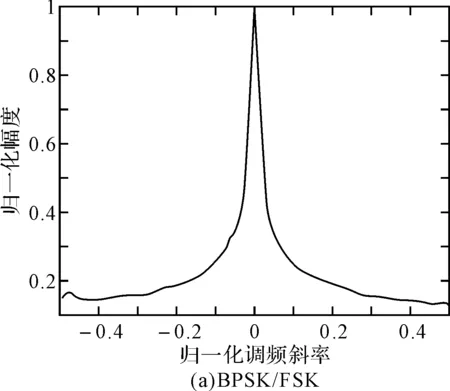
图2　各信号的PFRFT变换对应周期下的调频斜率与幅度的关系图

由图2可知利用信号检测PFRFT变换的结果可以粗略将信号分为两类,第一类包括Frank码、P1码、P2码、P3码、P4码、LFM信号(如图2(b)所示),它们的调频斜率不为0,结果会在对应调频斜率不为0的位置取得最大值;第二类为包括BPSK和2FSK信号(如图2(a)所示),为调频斜率为0的信号,在进行PAHT变换时会在对应调频斜率为0时取得最大值。

3.3第一类信号的识别

通过上节的讨论完成了信号的粗分为两类,其中第一类信号表现为调频斜率不为0。图3给出了各信号在对应最佳PFRFT变换域内的幅频关系,其中横轴表示分数阶域采样点数,纵轴表示归一化幅度,当改变频率时不改变信号的各脊线的比值关系,只是峰值所在位置发生改变。图中按幅度由大至小的四个分量依次用X(u1)、X(u2)、X(u3)、X(u4)来表示,定义如下变量:

(6)

(7)

由式(6)、(7)可知Ratio1表示信号在分数阶域的最强信号分量与次强分量能量之比,Ratio2则表示最强分量与其余三个分量的能量之比。表1列出了图中第一类LPI雷达信号Ratio1及Ratio2关系。

　

　

信号LFMFrankP1P2P3P4Ratio1—1.069219.05249.74731.000419.0690Ratio2—0.92797.41114.29850.87648.5674

由图3及表1可知利用信号在最佳分数阶域内的幅频关系可以完成对第一类信号的识别。具体识别过程为:在最佳分数阶搜索归一化幅度超过0.8的峰值,统计峰值数N,当N=2时则为Frank码或者P3码,然后计算Ratio2,当Ratio2>0.9时判为Frank码否则为P3码;当N=1且超过归一化幅度0.15的峰值数S也为1时,则信号为LFM信号,若不为1则计算Ratio1,若Ratio1<12,则判为P2,否则计算Ratio2,若Ratio2>8则为P4码信号,否则为P1码。

3.4第二类信号的识别

考虑到BPSK和2FSK两种信号的调制方式,其中BPSK是由固定载频信号进行调制而得,而2FSK信号则是采用了两个频率进行编码的方式得到。因此可以利用信号的功率谱分布特征完成信号的分类。利用AR模型进行功率谱估计具有较高的准确性和抗噪性,因此本文选用AR模型对第二类信号进行谱估计来完成进一步的识别,估计阶数选为32阶。图4给出了这两种信号利用Burg递推法得到的AR模型功率谱。图中可以清晰地分辨BPSK和2FSK信号。为了提高算法的抗噪性,避免噪声对峰值判断造成影响,将峰值检测门限设置为最大值的3/5,当检测到峰值数为1时则判为BPSK信号,当检测到峰值数为2是则判为2FSK。

图4　第二类信号的AR功率谱图

4　算法总体流程

根据上一节对各信号波形特点的分析及分类识别的研究,现给出本文所提出的波形判别方法的具体流程,具体分类识别步骤如下:

步骤一:首先利用PAHT变换结果,进行二维搜索判断信号的谱峰位置,得到信号的调频斜率信息,当调频斜率为0时,为第一类信号(LFM、Frank码、P1/P2/P3/P4码信号),当调频斜率不为0时,则信号对应为第二类信号(BPSK,2FSK);

步骤二:若经过步骤一得到信号为第一类信号,则需对信号进行PFRFT变换,利用步骤一的结果对剩余两维进行搜索,求在最佳变换与内得到信号幅频关系,若归一化幅度值超过0.5的峰值个数为1则为LFM/P1/P2/P4信号,此时判断归一化幅度值超过0.15的峰值数若为1则为LFM信号,若不为1则Ratio1<12时为P2码,当Ratio1>12且Ratio2>8时为P4码,当Ratio1>12且Ratio2<8则为P1码;若归一化幅度值超过0.5的峰值为2则为Frank/P3码,此时若Ratio2>0.9,则为Frank码,否则为P3码。

步骤三:若经过步骤一得到信号为第二类信号,则需要对信号功率谱进行估计,估计模型为32阶AR模型,对估计得到的功率谱进行峰值检测,检测门限选为最大峰值的3/5,假设检测到两个峰值则判为2FSK,若检测到1个峰值则判为BPSK;其对应的具体流程图如图5所示。

5　仿真实验及结果分析

为验证本算法的有效性与正确性,现对LFM、Frank、P1～P4码、BPSK、2FSK等8种信号进行分类识别实验,其中信号载频为1MHZ(2FSK为1MHZ和1.5MHZ),采样频率为5MHz,多相码码长为64位,BPSK信号为13位Barker,码宽为1μs,LFM信号的脉宽为T=13μs,B=5MHz。选取高斯白噪声作为背景噪声。

实验一:截获信号周期数M=1,信噪比范围取-8dB～3dB,信噪比间隔为1dB,每个信噪比条件下进行500次MonteCarlo实验,识别结果如图6所示。

由MonteCarlo实验结果可以看出,在M=1时,本文所提出的波形识别方法在较低信噪比下对各信号均取得了较为理想的识别效果。在SNR=-2dB时对各信号正确识别率达到了90%以上,并且随着信噪比的提高当SNR=0dB时对各信号的正确识别率达到了100%。仿真实验结果表明本文方法在低信噪比下对LFM和2FSK和BPSK信号的识别能力最好,而对P3/Frank码的辨别效果最差。主要原因为LFM信号在最佳分数阶域能量全部集中到一条脊线上,而P1/P2/P4信号在最佳分数阶域能量集中在一条主脊线和多条副脊线上,能量分布较为分散,而P3/Frank码信号包含两条主脊线能量最为分散,因此识别率较其他信号低。由于对2FSK及BPSK是通过功率谱估计完成识别,因此识别效果取决于功率谱估计的性能,与其选用的阶数有关。

图5　识别算法流程图

图6　M=1时不同SNR下的识别正确率

实验二:当截获信号周期数M=2其他条件不变时,实验结果及详细数据分别如图7所示。

图7　M=2时不同SNR下的识别正确率

由实验结果随着截获信号的周期数增加对信号的识别效果相应的得到改善约3dB,因此利用PFRFT来对LPI信号进行处理更为合适,有效地解决了当截获周期数不为1时的信号识别难题,并且可以识别效果随着截获周期增加得到相应改善。

6　结语

本文通过分析LPI雷达信号波形设计特点,针对当截获信号为多个周期时的波形识别难题,提出了一种基于PFRFT的波形判别方法。解决了当截获信号多个周期时的难题,首先利用调频斜率进行预分类,然后根据信号在分数阶域的幅频特征和AR模型功率谱估计来完成进一步的识别。当SNR=-2dB且截获单个周期信号时,对于各信号的正确识别率达到了90%以上。该方法有效地解决了现有分类识别算法无法对多周期信号识别及多相码信号识别的难题,取得了较好的分类识别效果,但是计算量相对较大,提高分类识别算法的速度,降低算法的复杂度将是下一步的研究重点。

参 考 文 献

[1] Gross F B, Connor, J. Comparison of detectability of radar compression waveforms in classic passive receivers[J]. IEEE Trans Aerospace and Electronic Systems,2007,43(2):789-795.

[2] Jennison B K. Detection of polyphase pulse compression waveforms using the radon-ambiguity transforms[J]. IEEE Trans on Aerospace and Electronic Systems,2003,39(1):335-343.

[3] 黄知涛,周一宇,姜文利.基于相对无模糊相位重构的自动脉内调制特性分析[J].通信学报,2003,24(4):153-160.

HUANG Zhitao, ZHOU Yiyu, JIANG Wenli. The automatic analysis of intra-pulse modulation characteristics based on the relatively nonambiguity phase restoral[J]. Journal of China Institute of Communication,2003,24(4):153-160.

[4] 曾德国,熊辉,龙柯宇,等.基于相位差分的脉内调制信号类型识别[J].电子测量与仪器学报,2009,23(10):85-90.

ZENG Deguo, XIONG Hui, LONG Keyu, et al. Recognition of intra-pulse modulation signal types based on phase difference[J]. Journal of Electronic Measurement and Instrument,2009,23(10):85-90.

[5] 李明宴,张鲁筠,江铭炎,等.复杂脉内调制雷达信号的识别方法[J].计算机工程与应用,2011,47(15):156-160.

LI Mingyan, ZHANG Lujun, JIANG Mingyan, et al. Identification method for complex modulated radar signals[J]. Computer Engineering and Applications,2011,47(15):156-159.

[6] Swami A, Sadler B M. Hicrarchical digital modulation classification using cumulates[J]. IEEE Trans Commun,2000,48(3):416-429.

[7] 肖乐群,张玉灵,赵拥军.基于对角积分双谱的雷达辐射源信号识别[J].信息工程大学学报,2012,13(1):95-99.

XIAO Lequn, ZHANG Yuling, ZHAO Yongjun. Radar Emitter Signal Recognition Based on Diagonally Integral Bispectrum[J]. Journal of Information Engineering University,2012,13(1):95-99.

[8] PHILLIP E Pace. Detecting and Classifying Low Probability of Intercept Radar[M]. Norwood: Artech House,2009.

[9] 李宏,秦玉亮,李彦鹏,等.基于FrFT的LFM相参脉冲信号多普勒频率变化率估计算法[J].电子与信息学报,2010,32(11):2718-2723.

LI Hong, QIN Yuliang, LI Yanpeng, et al. A FRFT Based Algorithm for Doppler Frequency Estimation from LFM Coherent Rate Pulse Train[J]. Jouunal of Electuonics & Infoumation Technology,2010,32(11):2718-2723.

[10] 朱建东,赵拥军,唐江.线性调频连续波信号的周期分数阶Fourier变换检测与估计[J].电子与信息学报,2013,35(8):1827-1833.

ZHU Mingdong, ZHAO Yongjun, TANG Jiang. Periodic FRFT Based Detection and Estimation for LFMCW Signal[J]. Journal of Electronics & Information Technology,2013,35(8):1827-1833.

[11] 李昕,王向前.离散分数阶Fourier变换的LFM信号时延估计[J].系统仿真学报,2012,24(4):756-760.

LI Xin, WANG Xiangqian. LFM Signal Time-Delay Estimation Based on Discrete Fractional Fourier Transform[J]. Journal of System Simulation,2012,24(4):756-760.

[12] 宁辉,陈超.基于分数阶傅里叶变换的脉内信号调制方式识别[J].电讯技术.2011,51(12):42-47.

NING Hui, CHEN Chao. Recognition of Intra-pulse signals modulation based on fractional fourier transform[J]. Telecommunication Engineering,2011,51(12):42-47.

[13] 李建,张国毅,王长宇.复杂调制形式脉压雷达信号的识别方法[J].计算机工程与应用,2013,49(13):198-203.

LI Jian, ZHANG Guoyi, WANG Changyu. Identification method for complex modulated compression radar signal[J]. Computer Engineering and Applications,2013,49(13):198-203.

收稿日期:2015年10月11日,修回日期:2015年12月1日

作者简介:张柏林,男,硕士研究生,研究方向:航空电子侦察。

中图分类号TN911.7

DOI:10.3969/j.issn.1672-9722.2016.04.006

A Low Intercepted Signal Recognition Algorithm Based on PFRFT

ZHANG BolinXIONG ZhiweiWU Hongchao

(Aviation University of Air Force, Changchun130022)

AbstractAiming at modulation recognition problem for low probability of intercept radar signals, a new type of modulation recognition algorithm is put forward to complete the discriminator of eight kinds of LPI signals,including LFM, BPSK, 2FSK, Frank/P1/P2/P3/P4code. The preliminary classification is completed according to the presence or absence of signal frequency modulation slope through PFRFT. And utilization of primary and secondary domain Fractional ridge line, and the power spectrum estimation is used to complete the automatic classification of the signal. The flow chart and identify specific steps of classification algorithms are given. Simulation experiment shows that the algorithm has good recognition results and good effectiveness and feasibility.

Key WordsPFRFT, intra-pulse modulation, power spectrum estimation, low intercepted signal