K-means算法在隐语义模型中的应用*

范玉强　龙慧云　吴　云

(贵州大学计算机科学与技术学院　贵阳　550025)



K-means算法在隐语义模型中的应用*

范玉强龙慧云吴云

(贵州大学计算机科学与技术学院贵阳550025)

摘要隐语义模型(LFM)是文本挖掘领域的重要模型,将它应用于推荐系统的评分预测具有预测精度高和占用内存小的优点。但由于时间开销较大,LFM模型并不适合用于处理大规模稀疏矩阵。针对此问题,论文将K-means算法引入到LFM模型的评分数据处理,得到改进模型K-LFM。在K-LFM模型中,利用K-means算法对评分矩阵中的用户和项目数据进行聚类处理,然后重构评分矩阵降低原始矩阵的稀疏程度和矩阵规模,最后用重构后的评分矩阵训练模型,预测评分。通过在movielens数据集上实验发现K-LFM模型在运行时间上较LFM模型有大幅降低,而预测精度没有受到明显影响。

关键词隐语义模型; K-means算法; 评分矩阵; K-LFM

Class NumberTP391.1

1　引言

2　算法描述

2.1K-means算法

K-means是一种简单有效的经典聚类算法。算法采用计算属性距离的方式来度量样本属性间的相似性,距离越短则样本间的相似性越高。通过计算样本到簇心的距离可以将n个样本划分到指定的k个簇中。

算法:K-means(S,k),S={x1,x2,…,xn}

输入:数据对象集合S,聚类数目k

输出:k个聚类中心Zj及k个聚类数据对象集合Cj;

Begin

m=1;

initializeZj,j∈[1,k];

repeat

fori=1 tondo

begin

forj=1 tokdo

computeD(Si,Zj)=|Si-Zj|;

ifD(Si,Zj)=minD(Si,Zj) thenSi∈Cj;

end;

m=m+1

forj=1 tokdo

Until |Jc(m)-Jc(m-1)|<ε;

End

2.2LFM模型

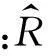
在训练集上以均方根误差RMSE作为指标,通过最小化RMSE可以学习获得P,Q矩阵使训练集预测误差最小[8]。即用优化的方法最小化损失函数:

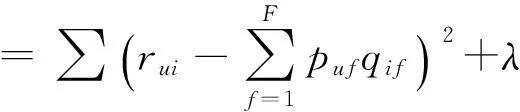
其中λ(‖pu‖2+‖qi‖2)是防止过拟合项,λ是正则化参数。

3　K-LFM模型

为了解决LFM模型在处理规模庞大的稀疏矩阵时效率较低的问题,K-LFM模型采用K-means算法处理评分矩阵。K-LFM模型分别从样本选取、重构评分矩阵和评分计算三个方面对LFM模型进行了修改。

3.1样本选取

LFM模型中样本的选取方法为:对单个用户U选取所有它有过行为的项目(正样本)和剩余的项目中随机的选取等量的项目(负样本)作为u的训练集K{(u,i)}[9～10]。这种取样方法减小了矩阵规模,但忽略了项目的完备性。在K-LFM模型的样本选取中,我们利用K-means算法将所有的用户和项目根据属性进行聚类,把聚类后的结果作为样本数据训练模型。

3.2重构评分矩阵

为了减小原始评分矩阵规模,K-LFM模型采用K-means算法重构评分矩阵。在计算用户类对项目类的评分过程中,活跃用户和热门项目对评分影响权较大。所以在重构评分矩阵过程中,以用户活跃度和项目流行度做为权重加权计算评分。

重构前的原始评分矩阵如图1所示。

由用户活跃度和项目流行度重构评分矩阵:

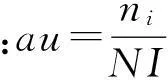
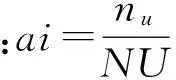
其中ni,nu分别为当前用户有过评分的项目数目和对当前项目评过分的用户数目;NI,NU分别为项目数量和用户数量。

用户ui对项目类Cij的评分计算方法:

(注:N(Ci)表示项目类Ci中元素的数量)

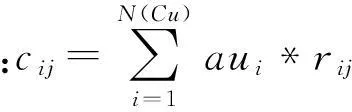
通过上述处理后原始评分矩阵和重构后的评分矩阵图2所示,其中k≤m,r≤n。

图1　原始评分矩阵

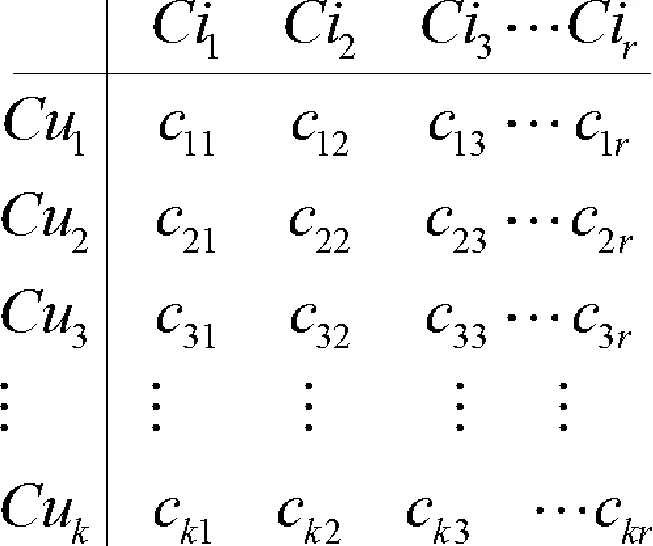
图2　分类后的评分矩阵

3.3评分计算

4　实验及结果分析

为了充分考虑用户和项目间的内在属性,实验数据集应当包含用户和项目的属性信息以及评分信息。Movielens数据集分为100K、1M、10M三个规模,分别包含了1000个用户对1700部电影的100,000条评分信息,6000个用户对4000部电影的1,000,000条评分信息和72,000名用户对10,000部电影的10,000,000条评分信息。本文采用100K规模的数据集进行实验,并将数据集按4∶1的比例分为训练集和测试集。训练集用来训练LFM的模型参数:隐特征个数(F),学习效率(α),正则化参数(λ),以及迭代次数(k);测试集用来测试模型的推荐效果。

4.1实验结果

在训练集上,根据用户的年龄、性别、职业等属性信息利用K-means算法将用户聚类;项目信息则根据影片题材进行划分。通过实验发现943位用户分为60类时具有较好的聚类效果。选取对分类影响最为显著的年龄和职业属性画出聚类结果如图3所示。在图3中,不同的形状和颜色分别代表不同的用户类,同一类中簇心用大图案显示。

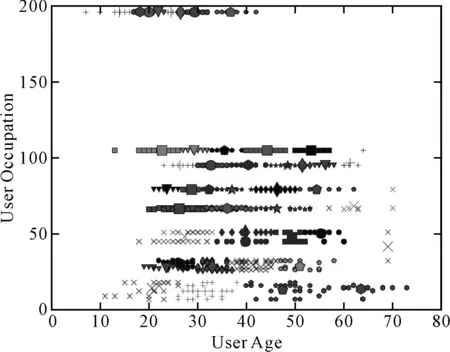
图3　用户聚类效果图

利用分类后的结果构造新的评分矩阵R′,原始评分矩阵为R。分别在R和R′上训练出LFM模型参数。通过实验我们发现隐含特征个数F对实验影响较大,固定α=0.002,λ=0.02,k=100。在测试集上,利用RMSE作为衡量指标得到LFM和K-LFM模型的预测精度如图4所示。

图4　模型预测精度

在实验环境为AMD FX(tm)-6100 CPU 4GB RAM电脑上。固定模型参数:F=45,α=0.002,λ=0.02。不同迭代次数下LFM模型和K-LFM模型的执行时间如图5所示。

图5　模型运行时间

4.2结果分析

通过实验发现LFM模型和K-LFM模型在预测精度方面,随着隐含特征数的增加,模型预测精度都有一定幅度的提高。在运行时间上,LFM模型的运行时间主要来自于模型训练耗时,所以运行时间与迭代次数成线性增长。而K-LFM模型的运行时间由K-means聚类和模型训练两部分构成。虽然K-means在处理数据过程中占据了部分运行时间,但它大大地降低了评分矩阵的规模,降低了模型训练的总耗时。所以在迭代次数较小的情况下,K-LFM的运行时间略高于LFM,而随着迭代次数的增加K-LFM的运行时间明显低于LFM模型。

5　结语

针对传统LFM模型在处理大规稀疏矩阵时效率较低的问题,本文将算法应用于LFM模型的评分数据处理,提出了K-LFM改进模型。通过实验发现K-LFM模型在没有明显损失预测精度的情况下,运行时间较LFM模型得到大幅降低。对于模型的推荐结果是否能更好地满足多样性和个性化的需求,将在下一步的工作中进行研究。

参 考 文 献

[1] Billsus D, Pazzani M J. Learning collaborative information filter[C]//Proceeding of International Conference on Machine Learning, San Francisco,1998:48-55.

[2] Paterek A. Improving regularized singular value decomposition for collaborative filtering[C]//Proceedings of KDD Cup and Workshop, California,2007:39-42.

[3] 方耀宁,郭云飞,兰巨龙.基于Logistic函数的贝叶斯概率矩阵分解算法[J].电子与信息学报,2014,36(3):715-720.

FANG Yaoning, GUO Yunfei, LAN Julong. A Bayesian Probablistic Matrix Factorization Algorithm Based on Logistic Function[J]. Journal of Electrionic & Informatiom Technology,2014,36(3):715-720.

[4] Koren Y. Factorization meets the neighborhood: a multifaceted collaborative filtering mode[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York,2008:426-434.

[5] Jian Cheng. Group latent factor model for recommendation with multiple user behaviors[J]. ACM July,2014.

[6] 张玉芳,毛嘉莉,熊忠阳.一种改进的k-means算法[J].计算机应用,2003,23(8):33-36.

ZHANG Yufang, MAO Jiali, XIONG Zhongyang. An Improved K-means Algorithm[J]. Computer Applications,2003,23(8):33-36.

[7] 鲁权,王如龙,张锦.融合领域模型与隐语义模型的推荐算法[J].计算机工程与应用,2013,49(19):101-103.

LU Quan, WANG Rulong, ZHANG Jin. Recommender algorithm combined with neighborhood model and Computer Engineering and Applications[J]. 2013,49(19):101-103.

[8] 项亮.推荐系统实践[M].北京:人民邮电出版社,2012:18-19.

XIANG Liang. Recommendation System Practice[M]. Beijing: Post & Telecom Press,2012:18-19.

[9] Rong Pan, Martin Scholz. Mind the Gaps: Weighting the unknown in Large-Scale One-Class Collaborative Filtering[C]//KDD’09, New York,2009:65-68.

[10] Quanquan GU, Jie Zhou. Co-Clustering on Manifolds[C]//KDD’09, New York,2009:269-274.

收稿日期:2015年10月8日,修回日期:2015年11月21日

基金项目:贵州省科学技术基金项目(编号:黔科合J字[2010]2100号);贵州大学引进人才科研项目(编号:贵大人基合字(2009)029号)资助。

作者简介:范玉强,男,硕士研究生,研究方向:人工智能与模式识别。龙慧云,女,副教授,研究方向:Web服务的形式化分析。吴云,男,副教授,研究方向:云计算。

中图分类号TP391.1

DOI:10.3969/j.issn.1672-9722.2016.04.002

Application of K-means Algorithm in Latent Factor Model

FAN YuqiangLONG HuiyunWU Yun

(College of Computer Science and Technology, Guizhou University, Guiyang550025)

AbstractLatent Factor Model(LFM) is an important model widely used in text mining. It has the advantage of high precision and low memory cost in rating prediction. However LFM model is not suitable for processing large-scale sparse matrix. In order to improve the performance, K-means algorithm is introduced to deal with rating data into LFM. This new model is called K-LFM. First of all, K-means is used to classify user and item information in K-LFM. And then the rating matrices are refactored to reduce the scale and sparse degree of orignal matrix. Finally training model with refactoring matix, can get predict rating. The experiment on public data set movielens shows that K-LFM model is superior to LFM model on processing efficiency. Besides, the prediction accuracy isn’t significantly affected.

Key Wordslatent factor model, K-means algorithm, rating matrix, K-LFM