基于浓度的粒子群算法在含分布式电源配电网重构中的应用
袁俊,曾斌,曾敏,王沾,邹亮
(1.中国南方电网超高压输电公司柳州局,广西 柳州 545000; 2.湖南电网公司长沙市望城区供电公司,湖南 长沙 410000; 3.广西电网公司崇左供电局,广西 崇左 532200; 4.广西电网公司桂林供电局,广西 桂林 541000)
基于浓度的粒子群算法在含分布式电源配电网重构中的应用
袁俊1,曾斌1,曾敏2,王沾3,邹亮4
(1.中国南方电网超高压输电公司柳州局,广西 柳州 545000; 2.湖南电网公司长沙市望城区供电公司,湖南 长沙 410000; 3.广西电网公司崇左供电局,广西 崇左 532200; 4.广西电网公司桂林供电局,广西 桂林 541000)
针对现有基于粒子群算法的配电网重构易陷入局部最优的问题,本文将一种基于粒子浓度的新型粒子群算法应用于含分布式电源配电网的重构,该方法基于粒子浓度对粒子群的更新进行引导,有效提高了粒子的全局搜索能力,优化了含分布式电源配电网的重构结果。对IEEE33节点标准算例进行了仿真计算分析,结果表明重构后最优解较大的降低了网络损耗,验证了论文中新型算法能有效应用于含分布式电源配电网的重构;对比基于标准粒子群算法的配电网重构结果,验证了论文中的重构方法有效提高了含分布式电源配电网的重构性能。
配电网重构;新型粒子群算法;粒子浓度;分布式电源;优化运行
1 引言
在能源危机与环境保护的时代潮流下,绿色能源以及节能减排逐渐成为世界各国关注的焦点。电力系统中,通过机组调度、最优潮流、变压器最优运行以及配电网重构等可以实现节能减排,其中配电网重构(distribution network reconfiguration)是电力系统最重要的节能减排方式之一,通过配电网重构通常可以配电网网损约10%~30%[1-2]。
配电网具有闭环设计、开环运行的特点,通常通过配电网重构来优化负荷供电路径,以实现配电网的经济运行[3]。配电网重构实际上就是一个多维多目标数学优化问题,现有的优化算法主要包括传统优化算法和基于人工智能的优化算法两大类,传统优化算法主要包括线性规划法、最优流法[4]等;基于人工智能的优化算法主要包括禁忌免疫算法、人工神经网络算法、遗传算法、蚁群算法、专家系统等[5-10]。
随着绿色能源、节能环保战略的进一步深入,分布式电源(DG)大量接入已成为配电网发展一种不可逆转的趋势,DG的接入使配电网网络结构更为复杂、更具随机性,较传统配电网优化运行含分布式电源配电网的优化经济运行更为复杂。粒子群算法是一种类似于遗传算法的基于迭代的智能优化算法,但较遗传算法更简单易于实现,并且没有太多参数需要调整,粒子群算法的这些特点决定了它适用于含分布式电源的配电网重构。文献[11-13]针对基于粒子群算法的含分布式电源的配电网重构展开了研究,文献提出的算法尽管有效提高了粒子群算法的收敛速度,但算法易陷入局部最优的问题并没有得到有效改善。本文将基于浓度的新型粒子群算法应用于配电网重构,其具有很好的全局性能,能够改善原有粒子群算法易“早熟”的缺陷,有利于进一步促进含分布式电源配电网的经济优化运行。
2 配电网重构数学模型
2.1 目标函数
配电网重构的主要目的是降低网损、消除过载、平衡负荷、提高电压质量,本文以正常运行状态下网损最小为目标函数,表达式为:
(1)
Ri—支路i的电阻;
Pi—支路i流过的有功功率;
Qi—支路i流过的无功功率;
Vi—节点i的电压;
n—网络节点数。
2.2 约束条件
为优化配电网的经济优化运行,主要有节点电压约束、支路过载约束、开关操作次数约束及网络辐射状约束等约束条件。
(1)节点电压约束
Vimin≤Vi≤Vimax
(2)
Vimin—节点i电压的下限值;
Vimax—节点i电压的上限值。
(2)支路过载约束
Si≤Simax
(3)
Si—支路i流过功率的计算值;
Simax—支路i流过功率的上限值。
(3)开关操作次数约束
NSO≤NSOmax
(4)
NSO—一定时间内的开关操作次数;
NSOmax—一定时间内的最大开关操作次数。
(4)网络辐射状约束
设计、开环运行的方式,重构后网络应呈辐射状,无环路、孤立节点及孤岛存在。
2.3 DG模型
DG接入点主要考虑电动汽车、储能电池、风力发电以及太阳能发电等分布式电源的存在,各种分布式电源间的协同控制基本可以保证DG接入点为电网输出恒定功率,本文中考虑每一DG接入点的容量恒定为400kVA。
3 基于浓度的粒子群算法
美国社会心理学家J.Kennedy和电气工程师R.C.Eberhart通过对简单社会系统的模拟,于1995年在IEEE国际神经网络学术会议提出了粒子群(PSO)算法。粒子群算法类似于遗传算法,通过迭代寻求最优解,其主要通过粒子在解空间追随最优粒子搜索来寻求最优解,没有遗传与变异的过程,具有容易实现、参数少、搜索速度快、优化性能好等优点[14]。
标准粒子群算法虽然具有容易实现、搜索速度快、优化性能好等优点,但由于其是根据全体粒子和自身的搜索经验寻求最优解,越到进化后期粒子多样性丧失越严重,导致粒子群易陷入局部最优,出现早熟现象,这将影响配电网重构的最优性,影响配电网的最优经济节能运行。针对基于标准粒子群算法配电网重构的固有缺陷,本文将基于浓度的新型粒子群算法应用于配电网重构,一定程度上提高了算法的收敛速度,改善了算法易陷入局部最优的缺陷,能有效提高配电网运行的经济性[15]。
3.1 粒子浓度的概念
为了保证重构方式的多样性并避免算法早熟现象的发生,本文将基于浓度的新型粒子群算法应用于含分布式电源配电网的重构。基于浓度的新型粒子群算法定义第i个粒子的浓度为:
(5)
由公式(5)定义基于浓度的粒子选择概率为:
(6)
式(5)、(6)中xi与f(xi)分别表示第i个粒子及其适应度函数值,由式(6)可知,粒子i被选中的概率与粒子i的浓度成反比。即浓度越大,被选中的概率就越大,反之则被选中的概率越小。这使低浓度的粒子个体在迭代中不至于迅速被淘汰,有效保证了粒子的多样性。
3.2 粒子群的更新策略
3.2.1 标准粒子群算法的粒子群更新策略
假设一个由M个粒子组成的群体在D维所搜空间以一定的速度飞行。粒子i在t时刻的状态属性设置如下:

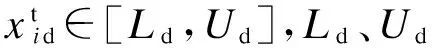

其中1≤d≤D,1≤i≤M。
粒子在t+1时刻位置更新:
(7)
(8)
式中,ω为权重系数;r1,r2为均匀分布在(0,1)区间的随机数;c1,c2称为学习因子,通常取c1=c2=2。
3.2.1 基于浓度粒子群算法的粒子群更新策略
粒子群更新初期按标准粒子群算法的更新方式更新粒子,当粒子群进化到一定程度时,为保证粒子群个体的多样性并避免粒子群早熟陷入局部最优,基于浓度粒子群算法引入了基于浓度的选择概率公式,其根据计算出的粒子浓度由高至低对粒子进行排序,对于浓度不一的粒子采用不同的速度更新方式。
对于浓度较高、选择概率较小的粒子,为避免陷入局部最优,因使其摆脱个体最优的影响,其速度按下式更新:
(9)
对于浓度较低粒子,为保证不过早被淘汰,保证粒子群体的多样性,避免粒子群早熟,应忽略粒子群体最优解对浓度低粒子的影响,而只受自身因素的影响,其速度按下式更新:
(10)
为了尽量避免粒子早熟,式(9)、(10)中的ω1、ω2与迭代次数的设置有关,具体取值方法将在下文中介绍。为了丰富粒子群体的多样性,算法对浓度适中的部分粒子进行初始化操作。
3.3 基于浓度粒子群算法流程

图1 改进粒子群算法的流程框图
4 基于新型粒子群算法的配电网重构
对于含有DG的配电网,可以利用基于浓度的新型粒子群算法对其运行进行优化,基于新型粒子群算法的含分布式电源配电网重构的主要流程如下:
(1)初始化,读入配电网原始数据,获得粒子群种群大小为M,粒子维数大小为D,设定粒子更新方式变化次数N(即当迭代次数达到N时,粒子采用基于浓度选择的算法更新),最大迭代次数为tmax,惯性权重系数ω,学习因子c1,c2;为取的更好的算法性能,本文中权重系数的设置采用从0.9线性递减到0.4的策略,线性递减公式如下:
(11)

(2)随机产生初始样本粒子群:随机生成M个可行粒子,并随机生成每一个粒子的初始速度,粒子初始速度的每一维为均匀分布于[0,1]间的随机数;
(3)根据每个粒子个体对应的网络结构进行潮流计算,并根据目标函数计算每个粒子的适应度值,将其适应度值与该粒子的个体最优位置比较,若较好,则更新当前位置为个体最优位置pb;然后再与整个粒子群的全局最优位置比较,若较好,则更新当前位置为全局最优位置pg,设当前迭代次数t=1;
(4)根据速度和位置公式(7)、(8)更新粒子的速度和位置,迭代次数t=t+1;
(5)判断t是否大于N,若t大于N,则转至步骤(6),若t小于N,则转至步骤(3);

(7)计算粒子群更新后各粒子的适应度值,并更新粒子群个体最优位置与全局最优位置,迭代次数t=
t+1;
(8)判断t是否大于最大迭代次数,若不大于,则返回至步骤(6);若大于,则输出全局最优位置,结束程序。
5 算例分析
本节以图2所示IEEE33节点配电网系统为例验证基于浓度的粒子群算法在含分布式电源配电网重构中应用的有效性[16]。该配电网共包含33个节点和37条支路,5个常开联络开关分别位于支路7-20、8-14、11-21、17-32、24-28上,配电网额定电压为12.66kV,总负荷为5084.26+2547.32kVA,设定接入DG输出功率可调控,数学模型可看作PQ模型,本文在13、17、21、32四个节点分别接入功率为400kVA,功率因数为0.9的DG。设定粒子群种群大小M=60,粒子维数D=37,N=15,最大迭代次数tmax=50,学习因子c1=c2=2。

图2 33节点配电网络系统
本文分别利用标准粒子群算法与基于浓度的新型粒子群算法对接入DG的IEEE 33节点配网系统与不接入DG的IEEE 33节点配网系统进行了仿真验证,并通过改变接入系统的DG容量进行网络重构以验证不同DG接入容量对于配网网损及节点电压的影响。仿真结果如表1所示。
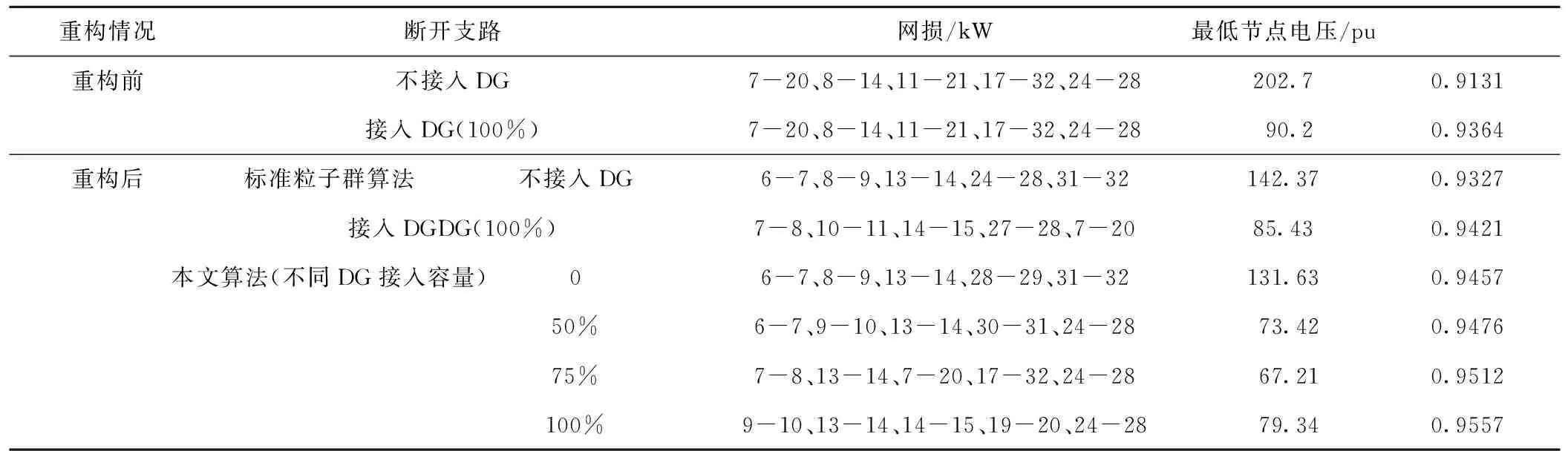
表1 配电网重构前后结果
由表1可知:(1)在不接入DG的情况下:一方面,重构后较重构前负荷均衡性能有了比较大的提高,网损有了很大程度的减小;另一方面,相比基于原始标准粒子群算法的重构方法,本文提出的重构方法得到的重构最优解网损更小,即其优化性能更优;(2)接入DG后,一方面,即使不进行配电网重构优化,配电网络的网损也有了明显的降低,节点电压也有了相应的提高,可见DG的接入提高了配电系统运行的稳定性与可靠性;另一方面,通过比较基于原始标准粒子群算法的配电网重构方法与本文提出重构方法的仿真结果,体现了本文提出方法具有更好的降损效果,具有更强的网络优化性能;(3)随着接入DG容量的不同,配电网络的网损也有差异,并且当容量增大到一定程度再增大时将增大配电网络的网损,原因在于此时DG相当于一个电源,容量过大时可能导致功率的多向流动,有可能增大支路的电流,从而增大了配电网络的网损,可见仅从配电网降损这一方面来说并不是接入DG容量越大降损效果更好。
6 结论
本文以网损最小为目标函数,将一种基于浓度的新型粒子群算法应用于含分布式电源配电网的重构,仿真结果表明:DG的接入有效提高了配电网络运行的稳定性与可靠性,但不同DG容量会引起不同的网损,且容量增大到一定程度时将增大配电网络的网损;无论配电网络是否接入DG,文中将基于浓度的新型粒子群算法应用于配电网重构均具有很好的运算效果,其全局优化性能优于基于原始标准粒子群算法的配电网重构方法,能有效降低配电网络的网损,提高配电网络运行的经济性。
[1] W.Wu,M.Tsai.Application of enhanced integer coded particle swarm optimization for distributionsystem feeder reconfiguration[J].IEEE Trans.on Power Systems,2011,26(3):1591-1598.
[2] 刘柏私,谢开贵,周家启.配电网重构的动态规划算法[J].中国电机工程学报,2005,25(9):29-34.
[3] 王承民,刘莉.配电网节能与经济运行[M].中国:中国电力出版社,2011,41-48.
[4] Dariush Shirmonhammadi,H.Wayne Hong.Reconfiguration of electric distribution networks for resistive line losses reduction[J].IEEE Trans.On Power Delivery,1989,4(2):1492-1498.
[5] S.Civanlar.J.J.Grainger,et al.Distribution Feeder Reconfiguration Algorithm for 1oss Reduction of Distribution Systems[J].EPSR.1992,19:137-144.
[6] 王征.基于负荷变化的配电网络重构[D].西安:西安理工大学,2007:59-65.
[7] 尹洪,刘天琪,李樊,等.基于免疫遗传算法的含分布式电源配电网重构[J].电力系统及其自动化学报,2014,4(26):15-19.
[8] Victor.Parada,JacquesA.Ferland,Miguel.Arias,et al.Optimization of electrical distribution feeders using simulated annealing[J].IEEE Transactions on Power Delivery,2004,19(3):1135-1141.
[9] 王法,刘茜,冯杰,等.基于多Agent禁忌免疫算法的配电网重构[J].华东电力,2014,42(8):1642-1646.
[10] Hoyong Kim,YunseokKo.Et al.Artificial Neural-Network based feeder reconfiguration for loss reduction in distribution systems[J].IEEE Trans.On Power Delivery,1993,8(3):1356-1366.
[11] 邱正美,马丽,张建华.基于Tabu-PSO的分布式发电配电网重构[J].电网与清洁能源,2010,26(10):39-42.
[12] 王佳佳,吕林,刘俊勇,等.基于改进分层前推回代法的含分布发电单元的配电网重构[J].电网技术,2010,34(9):60-64.
[13] 刘宏江,李林川,张长盛.基于多种负荷方式的含分布式电源的配电网重构[J].电力系统保护与控制,2012,40(10):117-121.
[14] 李丽,牛奔.粒子群优化算法[M].北京市:冶金工业出版社,2009,25-29.
[15] 李庆芳,孙合明.一种基于浓度的粒子群优化算法[J].重庆理工大学学报(自然科学),2012,26(12):79-83.
[16] Baran M E,Wu F F.Network reconfiguration in distribution systems for loss reduction and load balancing[J].IEEE Trans on PowerDelivery,1989(4):1401-1407.
Application of Particle ConcentrationbasedParticle Swarm Optimization in Distributionpower system Network Reconfiguration with Distributed Generations
YUANJun1,ZENGBin1,ZENGMin2,WANGZhan3,ZOULiang4
(1.China Southern Power GridEHV Power Transmission CompanyLiuzhou Bureau,Liuzhou 545006,China;2.Hunan Power Grid Corporation Changsha City Wangcheng Power Supply Bureau,Changsha 410000,China; 3.Guangxi Power Grid Corporation Chongzuo Power Supply Bureau,Chongzuo 532200,China; 4.Guangxi Power Grid Corporation Guilin Power Supply Bureau,Guilin 532200,China)
In order to improve the poor ability in global optimization of existing particle swarm optimization based distribution network reconfiguration.In this paper,a particle concentration based new-typleparticle swarm optimization was applied to network reconfiguration ofdistribution power system with distributed generations.Based on particle concentration,the particle swarms renewal is guided,which can effectively improved the global search ability of particles,and optimized the reconfiguration result.The simulation of IEEE 33 bus system shows that the optimal solution can reduce network lossesobviously,which verified the effectiveness of the method.After comparing with standard particle swarm optimization based network reconfiguration method,we achieved that the method in this paper effectively improved the reconfiguration performance of distribution power system with distributed generations.
distribution network reconfiguration;new-typleparticle swarm optimization;particle concentration;distributed generation(DG);optimizing operation
1004-289X(2016)06-0075-05
TM72
A
2015-09-19
袁俊(1988-),男,汉族,湖南娄底人,硕士,主要从事电力系统运行与控制方面工作; 曾斌(1988-),男,汉族,湖南娄底人,学士,研究方向为电力系统运行与控制; 曾敏(1989-),女,汉族,湖南益阳人,硕士,研究方向为电力系统保护与控制。

