基于最大似然的网络拓扑推断技术研究（二）

王 黎，张润生

（中国电子科技集团公司第五十四研究所，石家庄 050081）

基于最大似然的网络拓扑推断技术研究（二）

王 黎，张润生

（中国电子科技集团公司第五十四研究所，石家庄 050081）

（接5月刊）

3.2 广义似然比算法

我们可以通过广义似然比（GLRT）算法［15］构造假设检验来推断两个样本集合的总体均值是否相等。设有两个正态总体f1，f2，均值分别为μ1，μ2，方差为σ12，σ2

2，来自两个总体的抽样集合为S1=｛x1i，i=1，…，m｝，S2=｛x2i，i=1，…，n｝，样本容量分别为m，n，可以构造如下假设检验

H0： μ1= μ2= μ ， H1： μ1≠ μ2（3）

则样本数据关于参数集合｛μ1，μ2，σ1，σ2｝的似然函数为

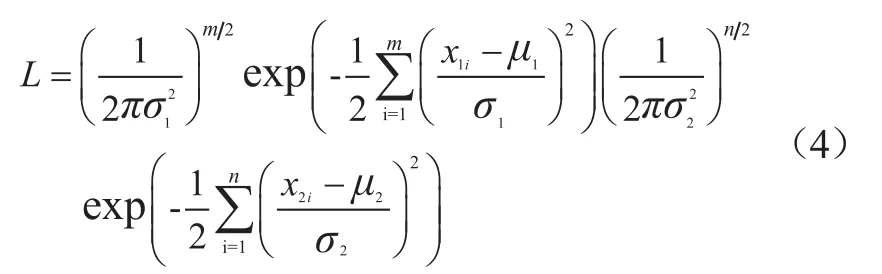
假设σ1

2= σ2

2= σ2得到

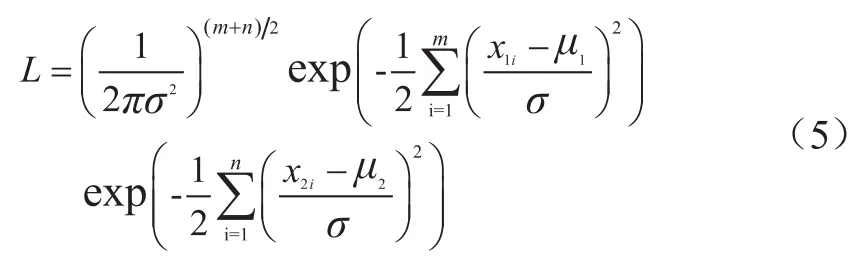
在假设H1下，似然函数可以用（5）式表示，可得μ1，μ2，σ2的最大似然估计为

将（6），（7），（8）式代入（5）得

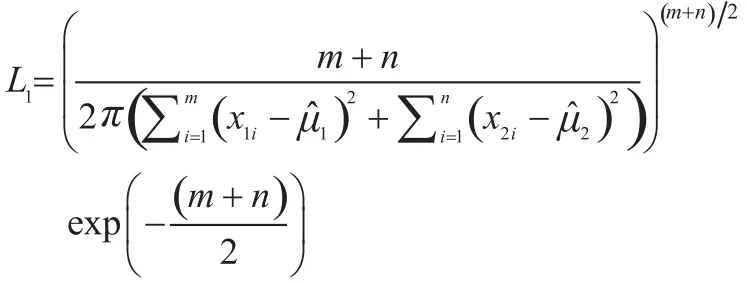
在假设H0下

由（9）可得μ和σ的最大似然估计为

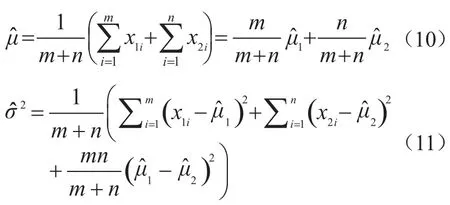
得

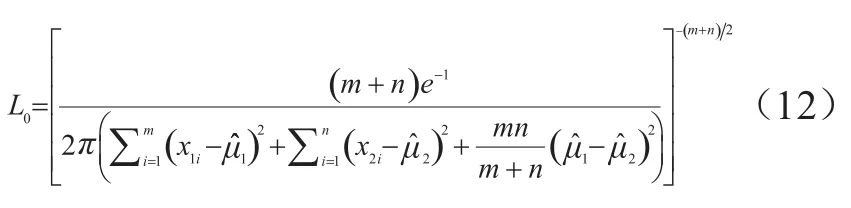
可得广义似然比为

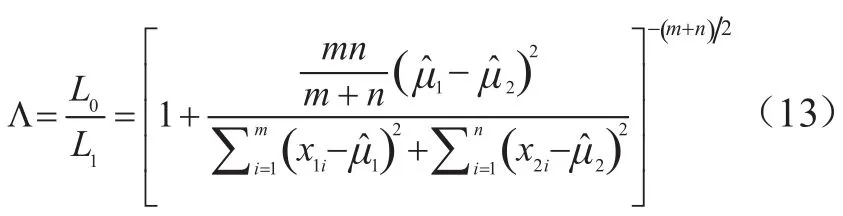
在假设H0下

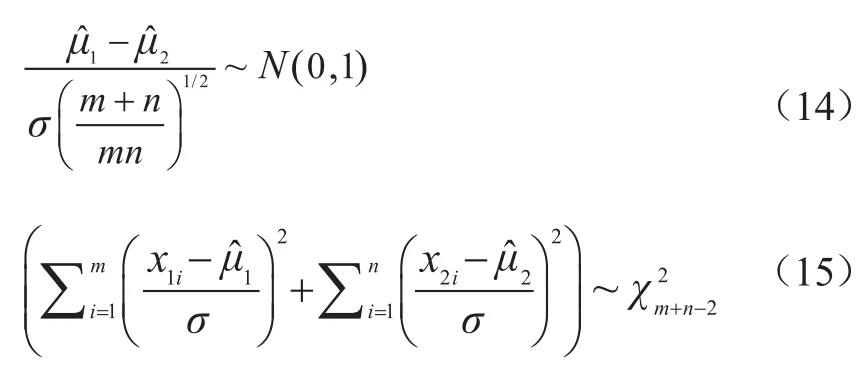
可得

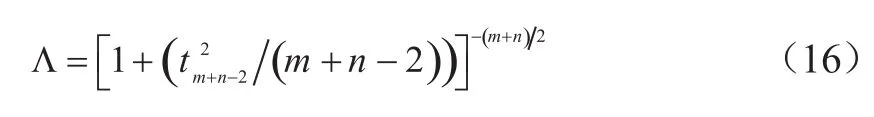
3.3 算法步骤

1）将所有叶子节点看成子树，即令S=D；

3）通过GLRT算法判断｛ i ， j ｝的合并方式，将｛ i ， j ｝合并成子树k，更新集合S，S=S｛ i ， j ｝k；

4）如果集合S中元素个数为1，则结束，否则返回步骤2）。

4　性能分析

通过分析第三节提出的算法，可以发现树状拓扑推断的正确概率由两方面决定，一是最相关子树寻找正确的概率；二是子树合并方式判断中假设检验的正确概率。

由于叶子节点相关性满足单调性，因此在理想情况下，寻找最相关子树不会发生错误，而实际中由于节点相关性测量误差的存在，在测量样本容量不大或者测量样本集合中存在较多野值时，最相关子树的寻找则可能发生错误，我们假设在序贯合并过程中，每次寻找最相关子树的平均错误概率为γ，则随着样本容量。

在判断子树合并方式的假设检验时，我们给定显著性水平为α，即检验犯第一类错误的概率（即两节点是同一节点的情况下，判定为非同一节点的概率）为α。下面我们推导犯第二类错误的概率（即两节点不是同一节点的情况下，判定为同一节点的概率），（14）（15）（16）式都是在假设H0的条件下得出，而在假设H1成立的条件下，设δ=μ1-μ2，则有

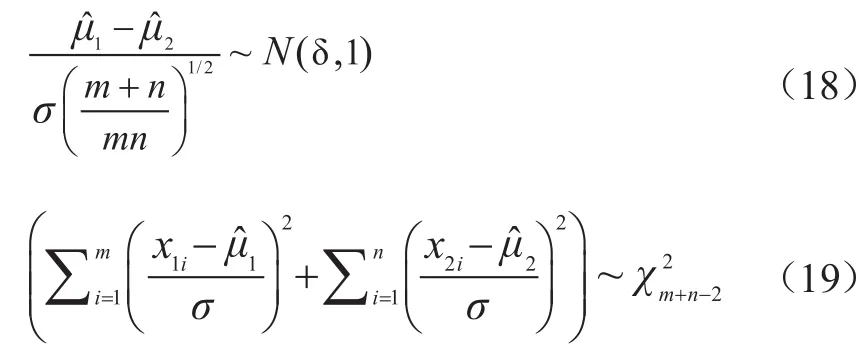
可得

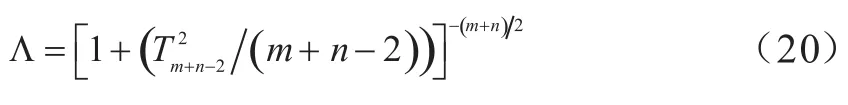
通过分析可得，整个序贯合并过程需要寻找最大相关子树Nr-1次，需要进行M-1次的假设检验，其中Nr为叶子节点个数，M为真实拓扑中内部节点个数。因此，基于假设检验的序贯拓扑推断算法的正确推断概率。

（未完待续）

The Technology of Topology Based on Maximum Likelihood （II）

Wang Li， Zhang Runsheng
（The 54th Research Institute of CETC ， Shijiazhuang Hebei 050081， China）

10.3969/J.ISSN.1672-7274.2016.07.009

TN911 文献标示码：A

1672-7274（2016）07-0022-02