加权马尔科夫链模型在水库含沙量预测中的应用研究

于秀凤，于保慧

（1.辽宁省白石水库管理局，辽宁 朝阳 122000；2.辽宁省水文局，辽宁沈阳110003）



加权马尔科夫链模型在水库含沙量预测中的应用研究

于秀凤1，于保慧2

（1.辽宁省白石水库管理局，辽宁 朝阳 122000；2.辽宁省水文局，辽宁沈阳110003）

［摘 要］本文用加权马尔科夫链模型预测水库含沙量，结合水库实测入库含沙量数据，分析加权马尔科夫链模型在水库含沙量预测精度。研究结果表明：加权马尔科夫链模型适用于水库含沙量的预测，在年尺度上预测值和实测值之间的相对误差在14.47%～19.25%，过程拟合系数0.7以上；在小时尺度上预测值和实测值之间的相对误差低于15%，过程拟合系数可达到0.65以上，预测精度符合入库含沙量预测规范的要求。研究成果对于水库含沙量预测方法提高参考价值。

［关键词］加权马尔科夫链模型；含沙量预测；模型适用性分析；水库

0　引　言

水库泥沙淤积一直是国内外学者关注的热点问题，对水库泥沙淤积进行定量评估和预测的前提需要对水库入库的含沙量进行准确的预测。对于水库入库含沙量预测大致分为两种方法：一种为采用物理模型进行模拟计算［1-3］，该方法的优点在于具有准确的物理意义，缺点在于需要大量的参数设置，且操作较为复杂；另一种方法基于水库实测的入库含沙量数据，采用数学模型，结合数量统计学的方法，寻找含沙量变化规律，依据一定的规律性，进行未来水库含沙量的预测［4-6］，该方法优点在于需求参数较少且操作较为简单，但缺点是需要进行水库较长时间序列含沙量的预测。当前，加权马尔科夫链模型由于需求参数较少，且在变量预测中不需要长序列的序列样本，在水资源领域中得到推广和运用，取得一定的研究成果［7-9］，但是在水库入库含沙量预测中的研究较少，为此，本文引入加权马尔科夫链模型，以辽宁某水库为实例，预测该水库2000—2010年入库含沙量过程，并结合水库实测的含沙量数据，分析加权马尔科夫链模型在水库入库含沙量预测的精度。该成果对于水库含沙量预测的方式和方法上提供一定的参考价值。

1　加权马尔科夫链模型原理

马尔科夫链先计算一组随机变量序列［x，t∈T］为随机生成的一组随机序列，在随机序列中：

对于任意时间变量t≥0以及随机变量的状态值j，i0，i2，i3，…，it-1（i1∈E），都代表

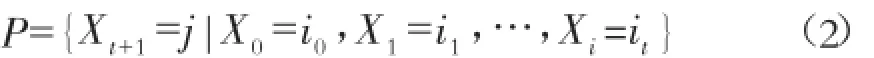
则表示［x，t∈T］为马尔科夫链。通过马尔科夫链的表达式可以看出，马尔科夫链表示的系统含义是t+s时刻变量的一个状态值只和前个t时刻的状态相关，而和t时刻以前的状态无任何关联。

传统的马尔科夫链未能考虑各个变量因子之间的权重系数，在收敛计算时存在收敛异常的情况。为此本文引入改进的马尔科夫链，改进的马尔科夫链主要是通过建立各个因子不同的转移概率权重，利用标准化的各因子的自相关系数作为转移概率权重，将变量的某一个时刻的状态转移概率进行加权，以加权后的概率作为变量在某个时刻的预测值。从而预测该变量标准化因子所处在的变量值。改进的马尔科夫链变量的径流预测的主要步骤为：

1）通过建立各个变量因子的不同等级的标准以及各因子变化转移的概率系数，采用标准方差法进行不同等级的标准化，通过这种方法来确定径流预测不同时刻的状态值。为计算不同等级下的各因子变化转移的权重系数，需要对各个因子的概率权重系数进行相关计算。

2）对各个影响因子进行相关系数的计算，相关系数计算公式为：

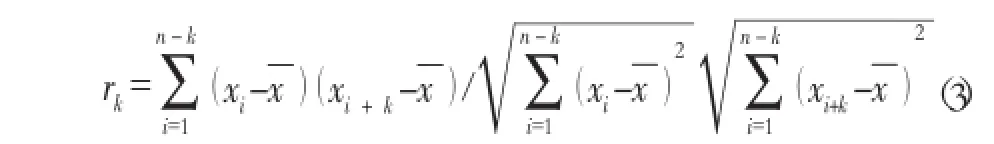
在公式（3）中xi表示的第i个时刻的变量状态值，在文中表示为径流值；x表示为径流的平均值。

对各个变量因子进行标准化处理，标准化处理公式为：

在公式（4）中m代表的物理意义为模型预测计算的最大因子数。

3）结合前面两个步骤中不同时刻的计算值作为初始的状态值，对应各个变量的转移概率加权权重系数，可以推算出下个时刻不同的状态变量值，其中K表示的模型计算时段的步长，本文选用年、月两个时间步长。

4）将处在同一个时间变量的状态预测值和各个因子的权重进行叠加计算，可以表示某个变量在该状态下的概率预测值，表达式为：

该时刻的计算最大概率值表示预测时刻对应下的状态值。

5）基于模糊数学的理论，将各个状态变量不同权重系数可以得到各因子的权重矩阵wi，则可以得到年径流的预测值，表达式为：

其中在方程（6）中T和B分别表示的变量状态的上下边界。

6）结合加权马尔科夫链的游历和方程稳定的特点，可以计算不同状态的变量概率值。

2　模型应用

以辽宁某水库为研究实例，应用加权马尔科夫链模型模拟水库入库含沙量，并结合水库1980—2010年实测入库含沙量数据，其中1980—2000年入库含沙量数据用于模型的参数的训练分析，2000—2010年的入库含沙量数据用于分析加权马尔科夫链模型在水库含沙量预测的精度。2.1年尺度入库含沙量预测对比分析

基于加权马尔科夫链模型，模拟水库2000—2010年入库年含沙量过程，并结合水库2000—2010年实测入库含沙量数据，分析加权马尔科夫链模型在水库含沙量预测的精度。分析结果见表1和图1。

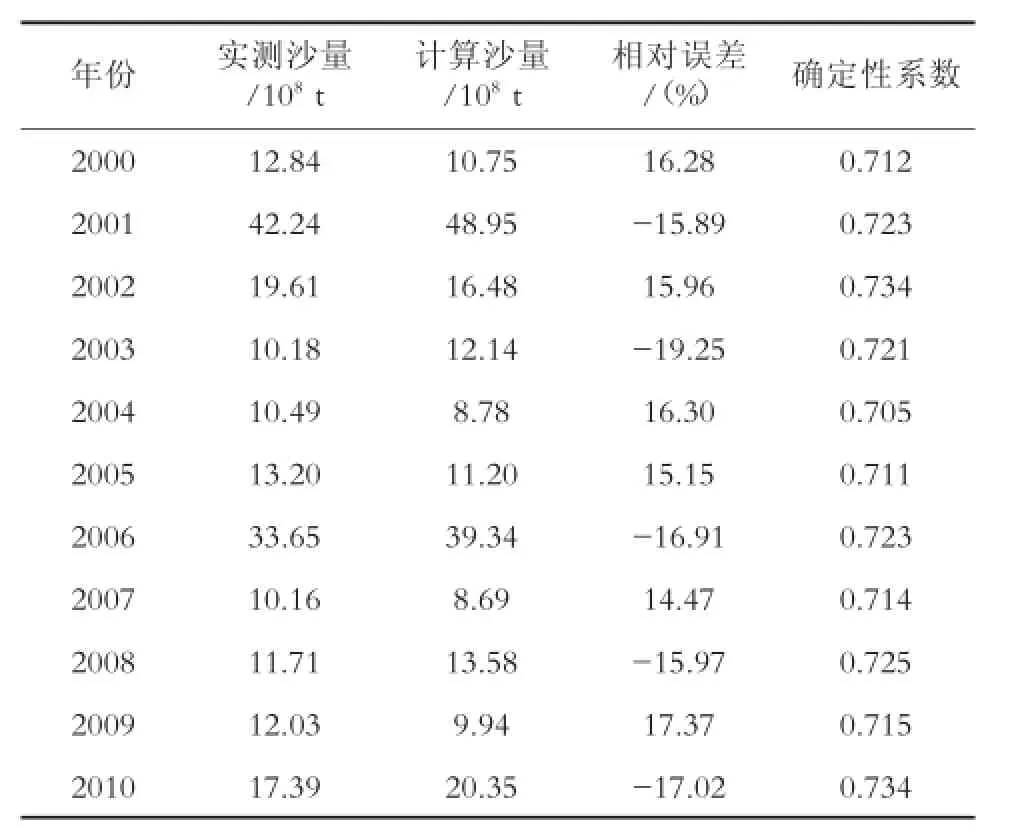
表1　加权马尔科夫链模型在水库入库年含沙量预测精度分析

图1　代表年份加权马尔科夫链模型在水库入库含沙量预测值和实测值过程对比图

由表1可以看出，加权马尔科夫链模型预测的水沙量和实测的沙量之间的相对误差在14.47%～19.25%之间，预测值和实测值之间的相对误差均在20%以内，在沙量上具有一定的精度，可以满足沙量计算规范要求，入库沙量预测计算规范要求为相对误差在25%以内。其次确定性系数是分析水库入库含沙量在过程上和实测入库含沙量在过程上的吻合度。从表1中可以看出，在2000—2010年加权马尔科夫链模型预测的水库入库含沙量过程和实测入库含沙量过程的确定性系数在0.705～0.734之间，确定性系数都高于0.7，可见加权马尔科夫链模型在含沙量过程上的预测也与实测入库含沙量过程较为吻合，这一点也可以从图1中看出。从图1中可以看出2001年和2006年，水库入库含沙量的峰值主要出现在水库的主汛期7月份和8月份，来水量相对较大，因此在这两个月份入库含沙量也相对较大，而加权马尔科夫链模型预测的含沙量过程的峰值也主要出现在7月份和8月份，和实测的入库含沙量过程拟合度较高。综上可见，对于水库入库含沙量年尺度上，沙量和含沙量过程都具有较好的吻合度。

2.2小时尺度含沙量预测对比分析

考虑到洪水过程中水库含沙量较多，为此本文在年尺度含沙量分析的基础上，结合水库10场入库洪水数据，基于加权马尔科夫链模型模型模拟了水库入库小时尺度的含沙量过程，结果见表2和图2。

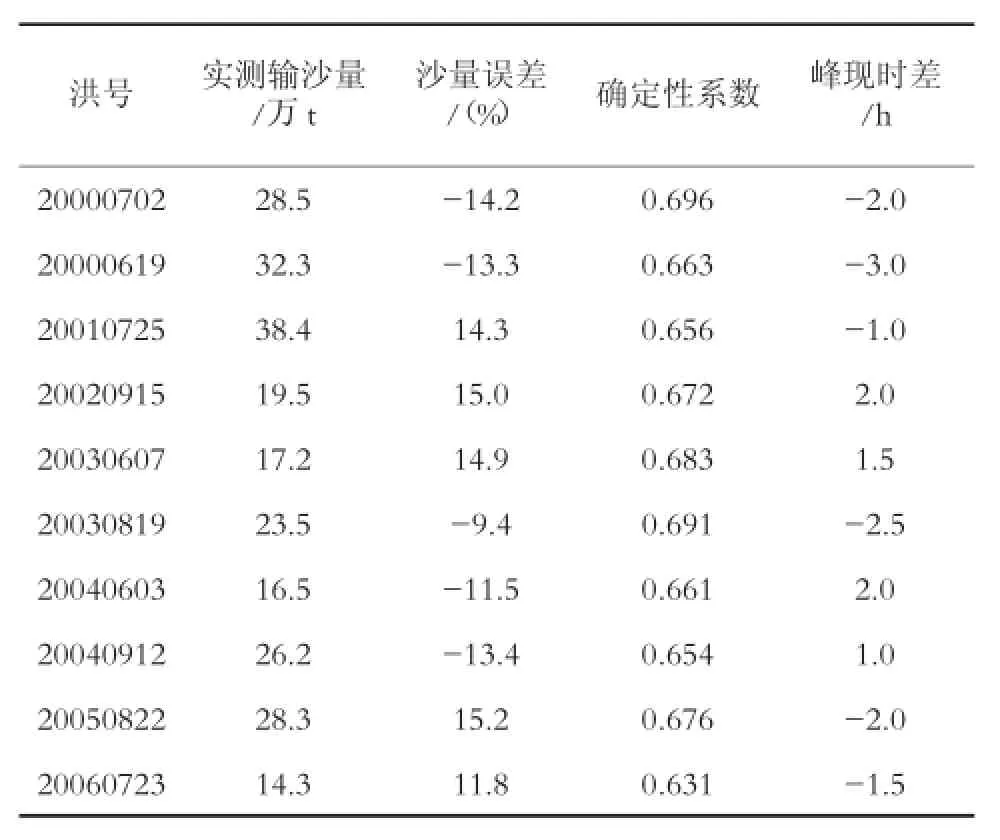
表2　加权马尔科夫链模型在水库入库小时尺度含沙量预测精度分析

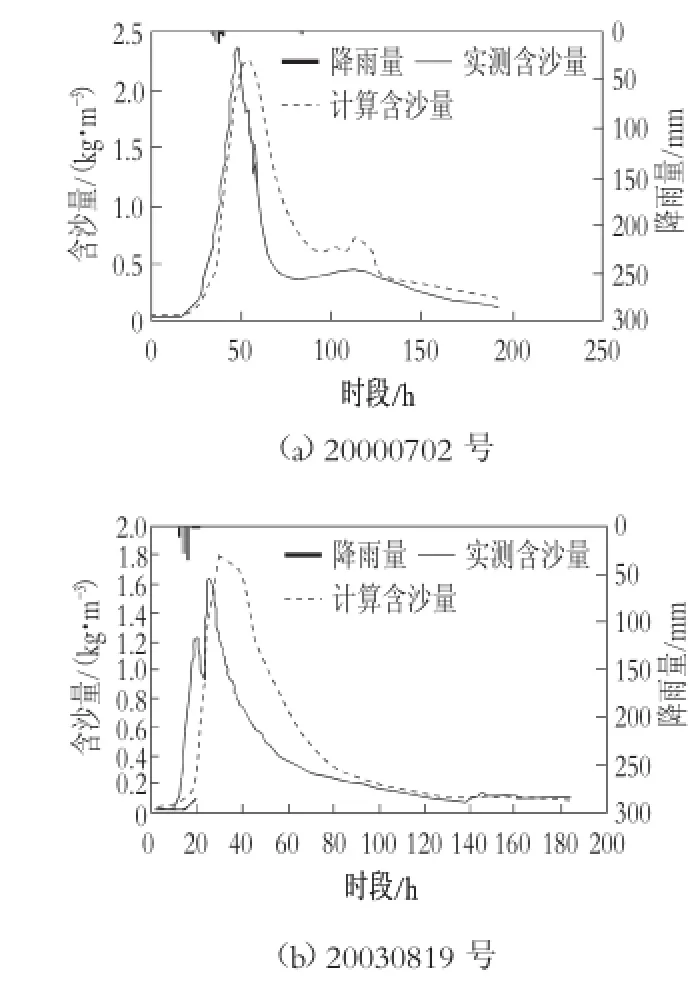
图2　加权马尔科夫链模型水库入库洪水场次含沙量预测值和实测值对比图

表2为采用加权马尔科夫链模型模拟水库10场洪水预测的含沙量，并和实测的水库入库数据进行对比分析，以实测值和模拟值之间的误差、次洪过程模拟的含沙量和实测含沙量的过程的确定性系数以及场次洪水沙峰出现时间的偏差作为模型场次洪水含沙量模拟的精度分析。从次洪含沙量预测结果可以看出，加权马尔科夫链模型预测的次洪含沙量和实测的含沙量之间的相对误差在-9.4%～15.0%。小时尺度含沙量预测相对误差模拟精度好于年尺度含沙量预测的相对误差，但是在次洪入库含沙量预测值和实测值在过程的相关系数均小于0.7，在确定性系数上差于年尺度预测值和实测值的相关系数，这主要是因为次洪含沙量计算时间较短，水量对含沙量的影响较强。在预测的含沙量沙峰出现时间偏差上，用加权马尔科夫链模型预测的沙峰出现时间和实测沙峰之间的误差在3 h之内，在沙峰出现时间上，具有较好的预测精度。从图2也可以看出，加权马尔科夫链模型预测的含沙量过程和实测的含沙量过程具有较好的吻合度。

3　结论

本文采用加权马尔科夫链模型对水库入库含沙量进行预测，并结合水库实测含沙量数据对比分析模型含沙量的预测精度，研究取得以下结论：

1）加权马尔科夫链模型可用于水库含沙量的预测研究，预测精度符合水库入库含沙量预测规范精度要求。

2）加权马尔科夫链模型在年尺度上预测的沙量和实测沙量相对误差差于小时尺度的相对误差，但在过程上吻合，年尺度预测值和实测值吻合度更高。

［参考文献］

［1］李亚娇.水库入库洪水预报与出库含沙量预测［D］.西安理工大学，2003.

［2］万新宇，包为民，王光谦.基于相似性的多沙水库坝址含沙量预测［J］.水科学进展，2010（01）：36—42.

［3］张袁，付强，王斌.基于自由搜索的水库入库含沙量预测模型［J］.南水北调与水利科技，2012（03）：40-43，72.

［4］李亚娇，李怀恩，沈冰.基于RBF网络的冯家山水库出库含沙量预测研究［J］.西北农林科技大学学报（自然科学版），2005（10）：134—138.

［5］刘媛媛.多沙河流水库多目标优化调度研究［D］.天津大学，2005.

［6］曹爱武，顾圣平，何露，国栋.基于小波神经网络的水库泥沙预测［J］.江南大学学报（自然科学版），2015（03）：338—343.

［7］秦松.基于加权的滑动平均—马尔科夫预测模型及其应用［J］.水资源与水工程学报，2013（01）：185—188.

［8］杜川，梁秀娟，王中凯，肖长来，王亮.改进灰色-马尔科夫模型在年降水量预测中的应用研究［J］.节水灌溉，2014（06）：32—36.

［9］冯江浪.改进灰色马尔科夫模型及其在水资源预测中的利用［J］.物探化探计算技术，2010（01）：109—112，122.

［中图分类号］TV145；TV149.2；P332.5

［文献标识码］A

［文章编号］1002—0624（2016）07—0056—02

［收稿日期］2016-05-19