小学数学绘本中数学信息的间接呈现方式

彭丽文

（深圳市盐田区林园小学）

小学数学绘本中数学信息的间接呈现方式

彭丽文

（深圳市盐田区林园小学）

小学生常常“惧”数学，他们觉得数学知识严肃、枯燥、抽象。他们对解决具体的数学问题时如何获取信息、筛选信息存在困难，尤其是相对隐藏的、间接呈现的信息。利用小学数学绘本研究联想、推理、重组等多种间接呈现数学信息的方式，在提升教师的数学专业素养、帮助教师更好地开展数学绘本教学的同时，也为教师提升学生信息能力奠定基础。

数学绘本；数学信息；间接呈现方式

“直接”是指不经过中间事物，直接与既定对象而进行关联。“间接”是在与既定对象发生关联的时候，必须借助一个中间媒介才能产生关联的，没有中间媒介就不会产生关联。虽然间接呈现的数学信息的捕获、转化存在着一定的难度，对于小学生来说存在一定的挑战性，但在这一活动更富有趣味性，更能开拓学生的思维，激发他们的主观能动性，在解决“大坡度”的数学问题中获得更高的成就感。

一、联想呈现

1.由此及彼式

由此及彼式是联想呈现的一种表现方式。数学是一门系统的学科，旧知识的存在常常能成为获取新知识的一种依据。在学习中，面对新的问题，学生尝试通过回忆、联想建立新旧知识间的联系，结合已有的旧识去发现、探索出解决新问题的方法，从而建立新知。

在平行四边形面积计算的相关绘本《歪歪的世界》学习中，平行四边形面积的计算成为孩子们的新挑战。

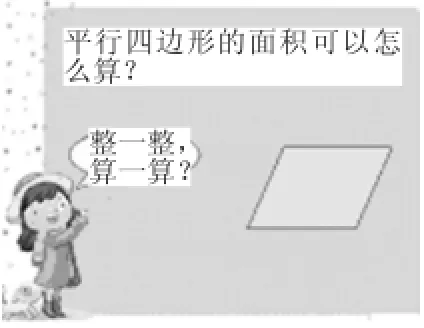
图1　数学绘本《歪歪的世界》

根据图中少量的数学信息如何求出这个平行四边形的面积？讨论中，学生尝试将它和已有的知识建立联系。如，将平行四边形的面积计算和长方形、正方形、三角形面积的计算联系起来，尝试将图形割一割、移一移、分一分。聪明的学生会想到在图上画出一条对角线，平行四边形就变成两个相同的三角形。还有学生会想到用割补法，将它变成长方形。把这样，求平行四边形的面积将转化成求这两个三角形面积之和的问题或者是转化成求一个长方形面积的问题。

假如将平行四边形分成两个相等的三角形：

三角形面积=底×高÷2

平行四边形面积=三角形面积×2=底×高÷2×2=底×高

未知的知识和已知的知识通过联想思维建立的联系，大大降低了解决问题的难度。学生在由此及彼式的回忆、联想中轻松获取新知。

2.触类旁通式

“触类旁通”是指掌握某一事物的变化、趋势及规律，从而类推联想到同类事物的变化、趋势及规律。它拥有比“由此及彼”更丰富的想象力，能将知识融会贯通，灵活运用。

绘本《小熊开店》是关于“口诀求商”数学知识的绘本，它讲述了小动物运用所学的数学知识解决小熊在商店中碰到的数学问题的故事。在故事中渗透了除法计算的方法多样性，突出用乘法口诀求商的方法的优越性。绘本中小伙伴们围绕问题：“20÷5=？”想办法，怎么算？

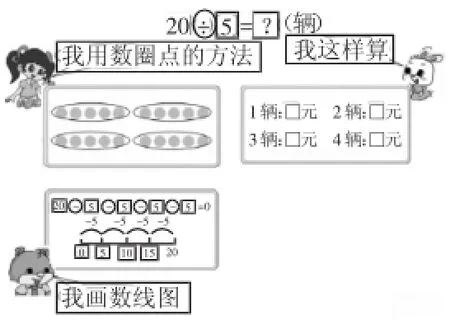
图2　数学绘本《小熊开店》

学生除了回忆起用画圆点、圈一圈；逐个加5；运用数线图等已掌握的老方法来解答，还可能根据“20÷5=？”这个已知除法信息联想到自己脑海中曾建构了关于5的乘法口诀的知识：四五二十。四五二十对应的乘法算式：4×5=20，也就是4个5相加等于20，反之20可以分成4个5，即20÷5=（4）。信息“四五二十”在大跨度的联想中呈现，让问题的解决变得更方便、快捷。

通过由此及彼的回忆、触类旁通的想象加工呈现出新的为学习所用的新的数学信息，这有利于学生温故知新、举一反三，在已有的数学知识网络中建构新的联想网络，锻炼学生动脑能力的同时提高学生的学习兴趣及效率。

二、推理呈现

1.演绎推理式

三年级长方形、正方形面积计算的相关绘本《数地砖》中，学生通过阅读绘本了解小人国的居民们用花瓷砖装饰家园并解决其中碰到的有趣的数学问题的故事。通过分小组模拟铺砖活动，学生发现并总结出长方形面积的计算公式：长方形面积=长×宽，运用公式能快速计算出长方形的客厅、卧室等地的面积，并计算出所用面积为1平方分米的瓷砖数量。绘本的最后留下了一个问题需要大家帮琪琪想办法解决：琪琪的洗手间是边长为8分米的正方形，面积是多少呢？需要几块面积为1平方分米的瓷砖？

图3　数学绘本《数地砖》

思考中，有的学生会发现：既然长方形的计算公式是“长方形面积=长×宽”，正方形又是特殊的长方形，它的四条边都相等，也就是“长=宽”，那么正方形面积就应该是边长乘边长，即“正方形面积=边长×边长”。学生通过已知的“长方形面积=长×宽”“正方形四条边都相等”这两个前提，得出“正方形面积=边长×边长”这一结论。结论通过演绎推理得出，绘本中具体的问题迎刃而解。

2.归纳推理式

归纳推理呈现则是从一些特殊数学信息归纳处理后总结出新的数学信息的过程，它是一个由特殊到一般的过程。在小学数学中，很多的运算定律、法则都是通过归纳推理总结出来的。

一年级的绘本《奇妙的计算》中有许多有待学生发现的奇妙的数学知识。如在开动大脑的活动中解决“99-99=？”“100-99=？”这两个问题。

图4　数学绘本《奇妙的计算》

图5　数学绘本《奇妙的计算》

绘本中没有直接呈现解决这两个问题的信息，需要学生去捕获、转化。学生通过计算左侧的算式，经过观察、比较后归纳总结出两个规律：（1）被减除和减数相同时，被减数-减数=0。（2）相邻的两个整数相减（被减数、减数），得数为1，进而推理出“99-99=0”“100-99=1”。富有逻辑的归纳推理，在激发学生探索兴趣的同时培养了他们有序、有理、有据思维的习惯。

3.类比推理式

类比推理呈现的是一种由“此”及“彼”的信息呈现过程。在呈现的两组或多组有着较多相似性的数学信息中，通过比较，根据其中一组数学信息具有的某一属性，从而推出另一组或其他组数学信息也该有相同或类似的属性。

在学习乘法的初步认识的相关绘本《和多拉一起去探险》中，学生和多拉一起玩闯关游戏，探索趣味数学中的秘密。

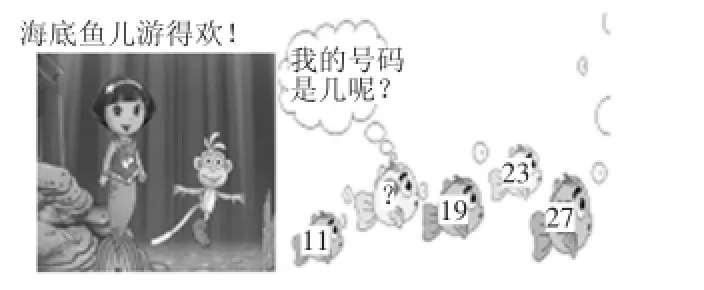
图6　数学绘本《和多拉一起去探险》

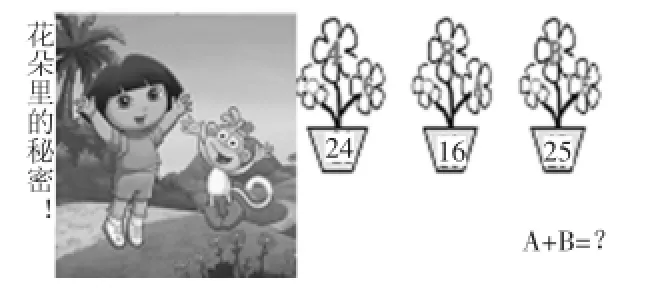
图7　数学绘本《和多拉一起去探险》

在“帮小黄鱼找号码”的活动中，齐列队的每条鱼儿身上带有1个号码，分别是11，（），19，23，27。第2只小黄鱼身上的号码丢失了，会是多少呢？直接呈现的数学信息只有“11，（），19，23，27”，怎么办？聪明的学生通过观察、比较、推理，发现列队中每相邻的两条鱼之间“相差4”的规律这一重要的数学信息，进而找到答案。还有部分学生从另一个角度观察到：小红鱼和小黄鱼是一一间隔排列的，每相邻的2条小红鱼或2条小黄鱼之间存在着“相差8”的规律这一重要的数学信息，进而解答。在“和多拉探索花园里的秘密”活动中，要解决A+B=？这一问题，图中也没有相关的直接数学信息。或许只要破解花盆里的秘密，找出数字A、B，我们才能找到答案。细心的孩子们发现第一个花盆中两朵花相乘的积就是花盆上的得数4×6=24，用类比的方法可以推理出8×A=16，A=2；B×5=25，B=5。找到A和B这两个重要的数学信息，A+B=？这个问题就迎刃而解。借助基础信息通过类比推理呈现出新的中间信息，能很好地为解答服务。

信息的呈现方式多种多样，直接呈现或许简单、具体、明了，但间接地通过推理去呈现新的信息的呈现方式对孩子的学习成长更是必不可少。

三、重组呈现

1.局部重组式

局部重组式即将小片段信息组合成局部信息的方式。

“乘法的初步认识”和“3的乘法口诀”是绘本中数学信息局部重组的最好的例子。绘本《买卖国的乘法队长》中，图文呈现信息：四个香蕉一捆，一共有五捆，香蕉的数量是“4+4+4+4+4”。商贩想了一种简单的记法：每捆数量×捆数，即4×5。学生在相同加数连加的现实场景中，认识了乘法算式，初步理解乘法意义，构建出数学信息片段：“4+4+4+4+4”，记为“4×5”，读作“四乘五”。后续逐个出现零散的数学信息片段：9个一盒的鸭蛋9盒记作“9×9”，读作“九乘九”；3瓶一捆的葡萄酒八捆记作“3×8”，读作“三乘八”……这些零散的数学信息帮学生积累了对“乘法意义”的感性认识，并总结出“每份数量×份数=总数”这一简便、快捷的计算多个相同加数连加的方法。

在学生认识了乘法的意义的基础上，学生阅读数学绘本《数学家阿汤的苦恼》，学习乘法口诀。结合绘本，学生能利用已掌握的知识轻松找出仙人掌每份的盆数、份数和总数间的关系。1捆是3盆：3×1=3；2捆3+3=6盆：3×2=6；3捆3+3+3=9盆：3×3=9。同类型数学信息重现、梳理，有序地将1个3、2个3、3个3相加表示为：3×1=3、3×2=6、3×3=9。通过局部重组，呈现了关于“3的乘法”的信息片段。

2.整体重组式

整体重组式即将局部信息再重组、整合成为整体信息的方式。

“九九乘法表”是绘本中将局部信息进行整体重组的好例子。

在数学绘本《数学家阿汤的苦恼》中结合图文一一呈现了“2-9的乘法”的局部信息后，绘本中聪明的阿汤按照从2到9的顺序最终编制了一个“神奇的九九乘法表”，2～9的乘法信息这一个个局部信息片段经过整体重组呈现。这种由点到线，由线到面的重组呈现形式，利于学生理解，通过梳理归纳、整理成表，便于学生记忆、使用。

这种数学知识、数学信息重组呈现的方式可以迁移运用到对所学知识的整理、梳理上。如，二年级长度单位的认识、学习等。数学的知识都是由知识点的学习，再到整条知识线的学习，最后汇集成知识网，通过对知识不断地充实、梳理、归纳、整理，学生形成愈加丰富的、愈加深刻的、系统的知识体系，这将便于学生理解、记忆，也便于学生以后的提取、运用。

数学绘本的阅读是小学生学习数学的一个良好的平台。在提高学生理解图文、分析问题等能力的同时，也大大提高了学生根据问题筛选出有效信息的敏锐度。

注：本文得到华东师范大学胡东方教授的肯定。

·编辑张珍珍