对流扩散模型的格子波尔兹曼方法及其应用*
郭孟琦 岳 军 黄 攀
(1.青岛理工大学 青岛 266520)(2.海军工程大学 武汉 430033)
对流扩散模型的格子波尔兹曼方法及其应用*
郭孟琦1岳军1黄攀2
(1.青岛理工大学青岛266520)(2.海军工程大学武汉430033)
摘要格子玻尔兹曼方法(LBM)是一种新兴的求解偏微分方程的数值工具,论文提出了一种基于对流扩散方程的图像去噪模型,并运用格子波尔兹曼方法对模型进行了求解。实验结果表明,该模型对含噪图像有着很好地去噪能力,同时还能很好的保持边缘细节信息。与P-M模型的AOS算法相比,在计算效率上有着较明显的优势,并且克服了处理前对阈值参数的选择,进一步地满足了图像处理中实时处理的要求。
关键词格子波尔兹曼方法; 对流扩散方程; 图像去噪
Class NumberP641
1引言
Lattice Boltzmann Method(LBM),即格子玻尔兹曼方法,是20世纪80年代中期建立和发展起来的一种流场模拟方法。LBM直接从离散模型出发,应用物质世界最根本的质量守恒、动量守恒和能量守恒规律,在分子运动论和统计力学的基础上构架起宏观与微观、连续与离散之间的桥梁,从一种全新的角度诊释流体运动的本质问题。
LBM与传统的计算流体力学方法(如有限单元法、有限差分法等)相比,其算法相对简单。简单的线性运算加上一个松弛过程,就能模拟各种复杂的非线性宏观现象。能够处理复杂的边界条件,压力可由状态方程直接求解。同时,它的编程容易,计算的前后处理也非常简单,具有很高的并行性,能直接模拟有复杂几何边界的诸如多孔介质等连通域流场,无须作计算网格的转换。因此,近些年它也成为了一种新的求解偏微分方程的数值工具。其求解偏微分方程的出发点是系统的微观模型,通过微观行为设计格子波尔兹曼方法的演化方程,在对系统进行模拟的同时实现对偏微分方程的数值求解。最早是钱跃竑[1]在1992年提出的,主要是用来求解Navier-Stokes方程的,现在已经在流体力学中得到了广泛的应用。
在图像处理应用方面,Jawerth B[2]运用LBM求解了非线性扩散方程。此方法在保证稳定性的情况下,能实现并行化以及大步长迭代计算以提高计算效率。Chang[3]根据变分模型提出了LBM去噪算法,严壮志等[8~11]通过在LBM的松弛因子中嵌入矢量图像的边缘特征,并定义新的平衡态分布函数,实现了矢量图像的非线性扩散去噪。2013年,柴振华等[12]提出了一种对流扩散方程的LBM。本文提出一种基于对流扩散方程的干涉图去噪新模型,并运用格子波尔兹曼方法对新模型进行了求解。实验结果表明,该模型对图像有着很好地去噪能力,同时还能很好的保持边缘细节信息。
2格子波尔兹曼方法
2.1格子波尔兹曼方法
格子波尔兹曼模型由离散化的计算网格构成,每个网格的值由粒子的分布函数fi(i=0,1,…,q-1)和扩散矢量构成,结构如图1所示。
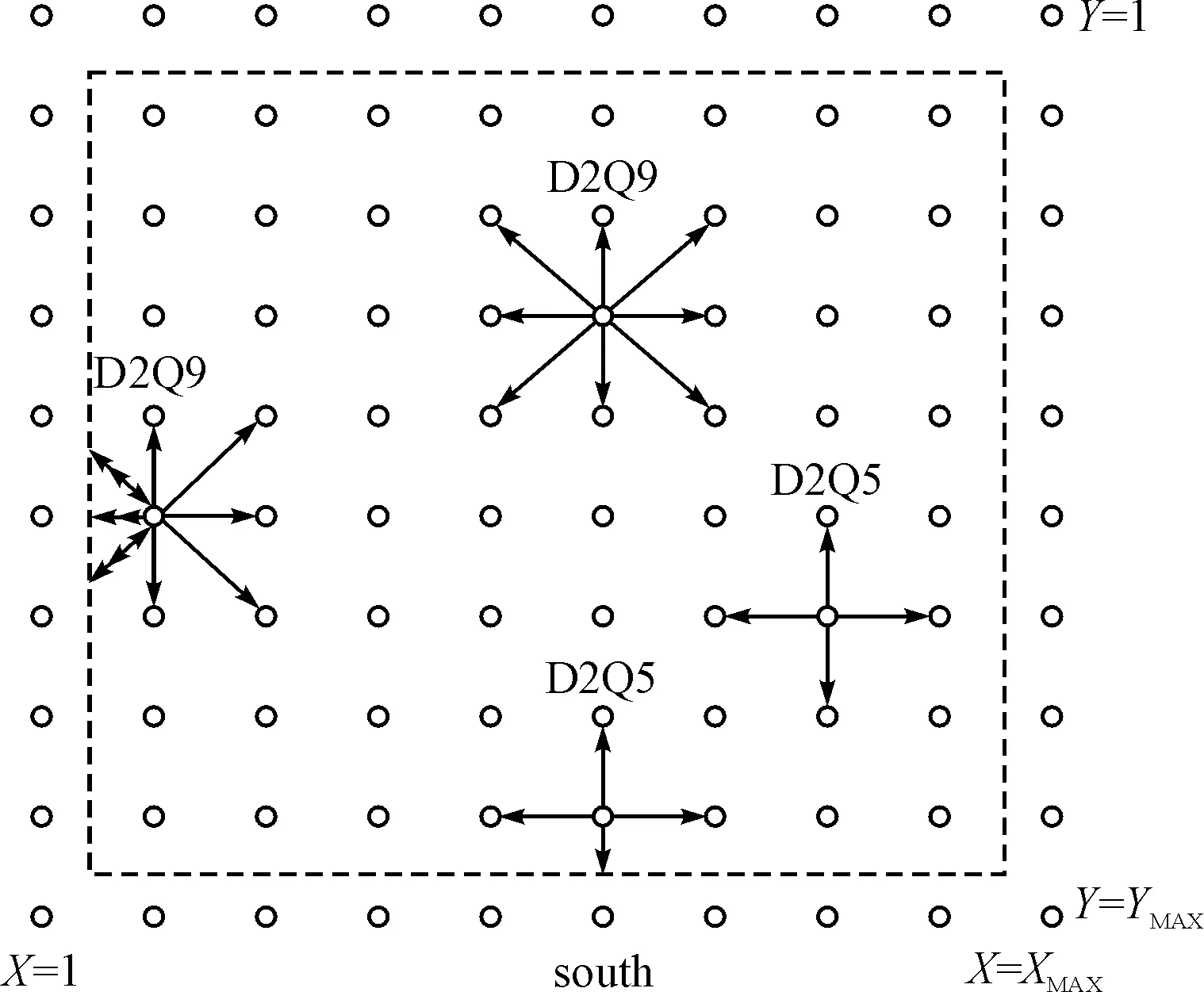
图1 LBM中D2Q5和D2Q9的结构以及半步长边界反弹格式原理图
(1)
对D2Q9模型:
(2)
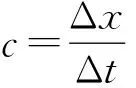
LBM的演化方程:
(3)
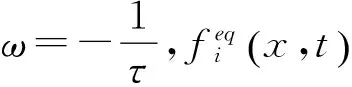
在整个扩散过程中,需满足质量守恒定律:
(4)
其中,I是图像强度(或图像灰度)。
设定D2Q5的平衡态分布函数为
(5)
D2Q9的平衡态分布函数为:
(6)
2.2对流扩散模型的格子波尔兹曼方法
鉴于格子波尔兹曼方法有着算法稳定,可进行大步长迭代,计算效率高等优点,下面对提出的对流扩散模型进行格子波尔兹曼演化。为了方便,本文把对流扩散模型的格子波尔兹曼方法记为LBCDM。考虑求解如下形式的一个偏微分方程:
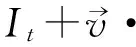
(7)
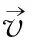

(8)

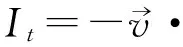
(9)
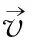
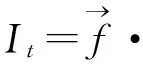
(10)
对方程式(10)做时域上的离散化,则可以做到:
(11)

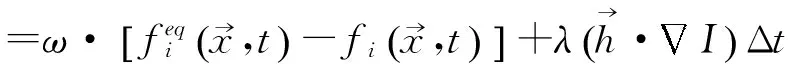
(12)
这里有:
(13)
以D2Q5为例,这里,αi=1/5,i=0,1,2,3,4。
首先,对方程式(12)的左边做泰勒展开:
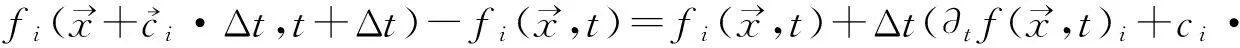
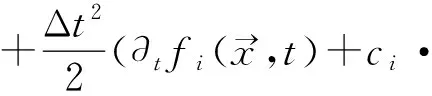
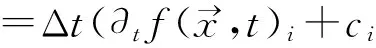
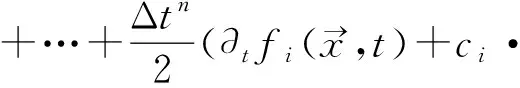
(14)
把式(14)代入式(12)中得:
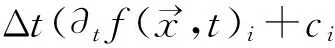
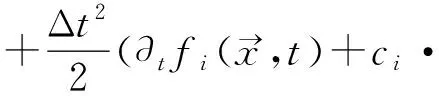
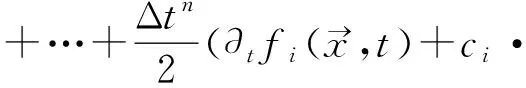
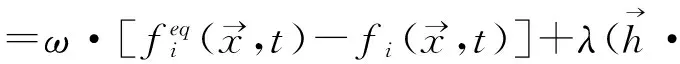
(15)
利用C-E展开并且代入到式(15)中,并在两边同时取O(ε2),可以得到:
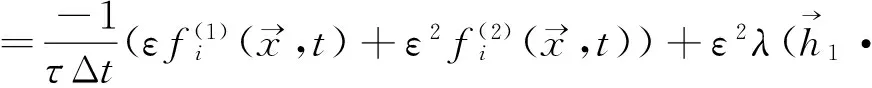
(16)
再对式(16)取O(ε),则可以得到:
(17)
而又因为有
(18)
在式(17)的两边对i求和可以得到:
(19)
再对式(16)两边取O(ε2),则可以得到:
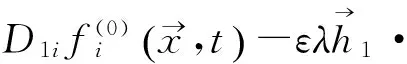
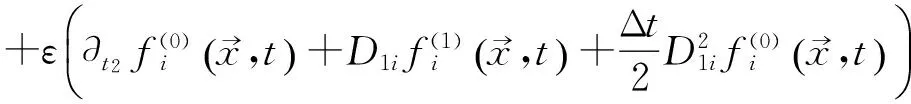
(20)
再把式(17)代入式(20),则有:
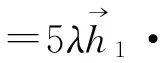
(21)
而由式(17)可以得到:
(22)
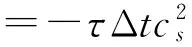
(23)
再把式(23)代入式(21),则有
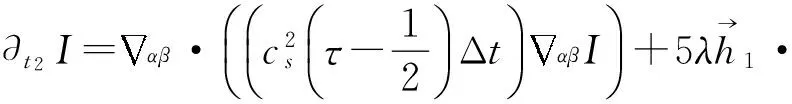
(24)

令式(18)乘以ε再加上式(23)乘以ε2则可得

(25)
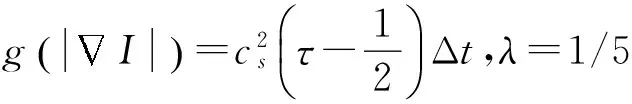

(26)

(27)
3数值实验结果与分析
把格子波尔兹曼方法下的对流扩散模型应用于图像去噪中去,与其他格子玻尔兹曼扩散模型的去噪算法进行比较。这里主要进行比较的模型是改进的P-M模型。
对一般的lena图分别用改进的P-M模型的AOS算法和对流扩散方程的格子玻尔兹曼算法(LBCDM)做数值实验,处理结果如下:
图2是经常用于图像处理的lena图,大小为500×500;图3对原图增加了十倍的随机噪声;图4、图5分别是两种去噪方法对加噪lena图的处理结果,其中时间步长选为0.05,LBCDM迭代次数为20次,边缘截止函数中的阈值为5,改进的P-M模型的迭代次数也为20次,高斯方差为1。

图2 原图

图3 十倍随机噪声图

图4 AOS算法的处理结果

图5 LBCDM的处理结果
从表1可以看出,对流扩散模型的格子波尔兹曼方法(LBCDM)计算时间上是明显优于改进的P-M模型的,这也充分地体现出了格子波尔兹曼方法的优势。其次,在噪声和迭代次数相同的情况下,LBCDM的残余点数少于改进的P-M模型,这就说明了LBCDM比P-M模型的AOS算法去噪能力稍强。最后,在具有较少残余点数目的前提下,LBCDM的边缘保持指数(EPI)也较P-M模型的更大一些,这就说明了LBCDM比P-M模型的AOS算法具有更好的边缘保持能力。

表1 不同降噪模型的处理结果对比
对湖试实验中得到的湖试噪声图分别用各向异性扩散模型的格子波尔兹曼方法(LBADM)、P-M模型的AOS算法和对流扩散模型的格子波尔兹曼方法(LBCDM)做数值实验,处理结果如下。
图6是从湖试试验中得到的带有噪声的湖试噪声图,大小为1080×4000;图7~图9则分别是三种去噪方法对湖试噪声图的处理结果,其中,时间步长均选为0.2,LBADM和LBCDM的迭代次数为3次,边缘截止函数中的阈值为5,P-M模型的迭代次数为5次,高斯方差为1。

图7 AOS算法的处理结果

图9 LBCDM的处理结果
从表3中首先可以看出,各向异性扩散模型的格子波尔兹曼方法(LBADM)和对流扩散模型的格子波尔兹曼方法(LBCDM)计算时间上是明显优于P-M模型的,这也充分地体现出了格子波尔兹曼方法的优势。其次,在具有较少残余点数目的前提下,LBCDM和LBADM的边缘保持指数(EPI)也较P-M模型的更大一些,这就说明了LBCDM和LBADM比P-M模型的AOS算法具有更好的去噪效果和更好的边缘保持能力。最后,LBCDM和LBADM相比,LBCDM相对具有更好的去噪能力和边缘保持能力。
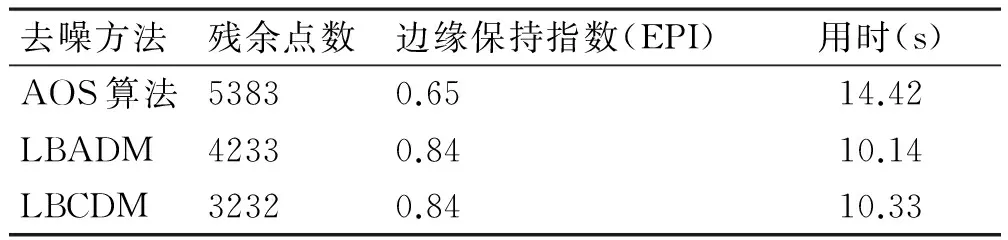
表3 不同降噪模型的处理结果对比
4结语
本文提出了一种基于对流扩散方程的图像去噪模型,并用格子波尔兹曼方法对模型进行了演化,即格子波尔兹曼的对流扩散模型。对图像进行了数值实验,实验表明格子波尔兹曼的对流扩散模型在图像去噪上有着很好的效果,同时对边缘细节信息的保持也有着较好的效果。通过对各向异性扩散模型的格子波尔兹曼方法(LBADM)、P-M模型的AOS算法和对流扩散模型的格子波尔兹曼方法(LBCDM)三种模型处理结果的比较,进一步地显示了对流扩散模型的格子波尔兹曼方法在图像的去噪效果、边缘保持以及计算时间等方面的优势,并且克服了AOS算法中处理前阈值参数选取的困难,进一步的满足了图像处理中实时处理的要求。
参 考 文 献
[1] Qian Y H, D’humieres D, Lallemand P. Lattice BGK models for Navier-Stokes equation[J]. Europhysics Letters, 1992,17(6):479-484.
[2]Jawerth,B.,Lin,P.,Sinzinger,E.:Lattice Boltzmann Method for anisotropic diffusion of images[J].J.Math.Imaging Vis.1999,11,231-237.
[3]Chang Qianshun, Yang Tong. A lattice Boltzmann method for image denoising[J]. IEEE Transactions on Image Processing, 2009,12(18):2797-2802.
[4]Huang Pan, Yue Jun, Chen Ming, Wang Maolin. Study of InSAS Interferogram Denoising Based on Partial Differential Equation[J]. Journal of Qingdao Technological University (in Chinese), 2011, vol.32(6).
[5]Koenderick I J.The structure of image[J].Biological Cybernet,1984,50(5):363-370.
[6]Wilson Au, Ryo Takei. Image Inpainting With The Navier-Stokes Equations [J]. Final Report APMA, 2001,2(8):28-30.
[7]Wenhuan Zhang,Baochang Shi. Application of Lattice Boltzmann Method to Image Filtering[J].Journal of Mathematical Imaging & Vision,2012,43(2):135-142.
[8]王志强,严壮志,张蕊,等.矢量图像去噪的格子玻尔兹曼方法[J].应用科学学报,2009, 37(3): 574-580.
[9] 王志强,严壮志,钱跃竑.图像非线性扩散去噪的格子玻尔兹曼方法[J].应用科学学报,2010,28(4):367-373.
[10] Chen Yu,Yan Zhuang-zhi,Qian Yue-hong.An anisotropic diffusion model for medical image smoothing by using the lattice Boltzmann method[C]//Asian-Pacific Conference on Medical and Biological Engineering,2008.IFMBE Proc.2008,19:255-259.
[11] 陈玉.格子玻尔兹曼模型及其在图像处理中的应用研究[D].上海:上海大学,2008.
[12] Zhenhua Chai, T.S. Zhao. Lattice Boltzmann model for the convection-diffusion equation[J].PHYSICAL REVIEW E,2013,87(6):1-15.
收稿日期:2016年1月8日,修回日期:2016年2月28日
基金项目:自然科学基金课题“多物理场图像处理与应用”(编号:61271015)资助。
作者简介:郭孟琦,男,硕士研究生,研究方向:图像处理的偏微分方程。岳军,男,博士,教授,研究方向:物理海洋中的偏微分方程。黄攀,男,博士研究生,研究方向:干涉合成孔径图像处理。
中图分类号P641
DOI:10.3969/j.issn.1672-9730.2016.07.013
Lattice Boltzmann Method and its Application of Convection-diffusion Model
GUO Mengqi1YUE Jun1HUANG Pan2
(1.Qingdao Technological University,Qingdao266520)(2.Naval University of Engineering, Wuhan430033)
AbstractThe lattice boltzmann method is an emerging tool for solving partical differential equations(PDE) a new image de-noising model is proposed based on convection-diffusion equations and the lattice boltzmann method is used to evolve the new model. Simulation experiment and real experiment data processing results and analysis show that the new model has a good de-noising ability on the interference figure and normal image. At the same time,it also can keep the edge details so well.Compared with P-M model of AOS algorithm, the new model has better computation efficiency and calculation result.
Key Wordslattice boltzmann method, convection-diffusion equations, image de-noising

