EXCEL在最小费用流问题中的应用

方江祎

【摘要】 EXCEL是日常办公软件Office的套件之一，除了常用的报表处理功能外，还有另外一个强大的功能就是管理决策和优化决策的应用。本文针对线性规划中的最小费用流问题，提供了物流配送网络的案例，使用最优化方法并利用EXCEL软件给出最小费用流问题的解决步骤和方法。

【关键词】 最优化问题 EXCEL 最小费用流

一、引言

近几年，网上购物的快速发展，使得物流行业成为国民经济中迅速成长的新兴产业。配送作为物流行业的重要组成部分，是物流业中最有前景和潜能的发展领域。如何合理安排和选择最优的配送线路，使得运输成本最低，成为物流业重要的研究课题。

Excel作为我们日常办公软件Office的套件之一，除了常用的报表处理功能外，还有另外一个强大的功能就是管理决策和优化决策的应用。EXCEL对于处理最优化问题，可以说是简单理解、方便操作的强大工具，也避免了非专业人员使用专业处理软件不熟悉等棘手问题。

本文以某物流配送网络作为最小费用流的研究对象，应用EXCEL软件进行分析和求解，达到对解决其他最小费用流问题举一反三的效果。

二、最优化问题

获得最佳处理结果的问题在数学中被称为最优化问题，这类问题的共同特点就是在所有的可能的方案中，选出最合理的，达到事先规定的最优目标的方案，这个方案是最优方案。针对最优化方案，寻找最优方案的方法称为最优化方法。

最优化方法是近几十年形成的，目的在于针对所研究的系统，求得一个合理运用人力、物力和财力的最佳方案，发挥和提高系统的效能及效益，最终达到系统的最优目标。

最优化方法由目标函数，约束条件和求解方法三个基本要素组成。

三、最小费用流

最小费用流是最优化问题中的一种，同时也是线性规划问题的特殊类型。我们通过建立线性规划模型并求解。

3.1 例子

假设有一物流配送网络，图1中标有LA的节点表示该公司的工厂，工厂共生产100个产品，要送往两个经销商，分别是图中标有LB和LC的节点，其中LB经销商需要60个产品，LC经销商需要40个产品。从LA工厂运送货物到LB和LC，中途会经过几个配送中转的仓库，在图中分别标为D、E、F、G节点，节点之间的弧代表运输路线。

在最小费用流问题中，管理者最希望得到的结果是每条路线运送多少产品，使得运输成本的总和达到最小。根据最优化方法，最小的运输成本总和为目标函数，约束条件则是要遵循的相关规则，解决方法是利用EXCEL线性规划求解。

图2是一个由7个节点，13条弧构成的有向图，图中任意一个箭头上方的数字表示这条运输线路的运输单价，箭头下方带有方括号的数字表示该条线路最大运输的容量。我们可以看到路线有很多条，并且每条路线的运输容量和成本都不同。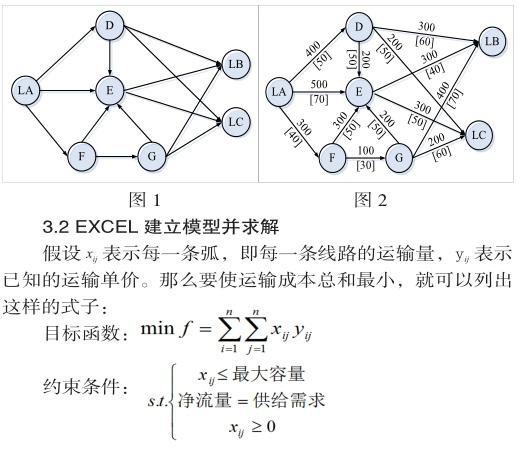

其中供给需求表示该节点上流出量减去流入量的值。

图3是根据该网络规划问题为基础得到的电子表格。

其中B列和C列列出了所有的弧，D列的运输数量表示要求的最优解，F列表示了每一条弧所对应的最大容量，G列是运输单价（价格/容量），D18单元格表示目标函数，在EXCEL中通过函数D18=SUMPRODUCT（运输数量，价格/容量）计算。J列列出了所有的节点，K列确定了每个节点所产生的净流量，在K3：K9中输入的等式用了两个SUMIF函数的差来表示净流量，第一个SUMIF计算该节点的流出值，第二个SUMIF计算该节点的流入值，两者之差就是净流量。

在线性求解参数对话框中，我们将“设置目标”为目标函数单元格，选择求解最小值，可变单元格为（D3：D15）。

之前我们列出的约束条件在这里表示为，第一组：D3：D15≤F3：F15，保证弧的流量不会超过该弧的最大容量；第二组表示为：净流量K3：K9=供给需求M3：M9。为了保证得到的最优解，即最优的运输量为正整数，要勾选“使无约束变量为非负数”。

另外在选择求解方法中选择单纯线性规划。通过求解，就得到了图6中的答案，最小的运输总成本为68000元，最优解就是D3：D15。

图6为得到最优解后，该物流配送网络的路线选择图，任意一个箭头上方的数字表示这条运输线路的运输单价，箭头下方的数字表示该条线路运输的数量。

四、总结

本文介绍了EXCEL线性规划在求解最小费用流问题的应用，既可以对单变量求解，也可以对多变量求解。通过对最小费用流问题的典型案例进行详细介绍，使用者还可以举一反三地解决最优化问题中的最短路径和最大流等问题。EXCEL对于管理者来说，不需要了解复杂的求解过程，只需把数据、目标函数、约束条件等在电子表格中设置好，即可以直接求得所需结果，符合管理者的实用价值，也使得EXCEL软件的使用价值大大提高。

参 考 文 献

[1] 朱德通.最优化模型与实验[M].上海：同济大学出版社，2003.

[2] 顾运筠.Excel规划求解的两类应用[J].计算机应用与软件，2005，22（1）：137-139.

[3]陈士成，李桥兴，何丽红.运筹学网络优化模型的Excel求解的减化方法[J].兰州：兰州大学学报（自然科学版），2010（46）：179-182.

[4]弗雷德里克.S.希利尔，马克.S.希利尔.数据模型与决策[M].北京：中国财政经济出版社，2003.

[5]冯英华.Excel平台下运筹学模型的求解分析[J].长春：长春工业大学学报（自然科学版），2014（4）：472-475.