Parameterization of Sheared Entrainment in a Well-developed CBL.Part II: A Simple Model for Predicting the Growth Rate of the CBL

Peng LIU，Jianning SUN*，2，and Lidu SHEN

1School of Atmospheric Sciences&Institute for Climate and Global Change，Nanjing University，Nanjing210023，China

2Jiangsu Provincial Collaborative Innovation Center of Climate Change，Nanjing210023，China

Parameterization of Sheared Entrainment in a Well-developed CBL.Part II: A Simple Model for Predicting the Growth Rate of the CBL

Peng LIU1，Jianning SUN*1，2，and Lidu SHEN1

1School of Atmospheric Sciences&Institute for Climate and Global Change，Nanjing University，Nanjing210023，China

2Jiangsu Provincial Collaborative Innovation Center of Climate Change，Nanjing210023，China

（Received 10 October 2015；revised 7 February 2016；accepted 23 May 2016）

Following the parameterization of sheared entrainment obtained in the companion paper，Liu et al.（2016），the present study aims to further investigate the characteristics of entrainment，and develop a simple model for predicting the growth rate of a well-developed and sheared CBL.The relative strati fi cation，de fi ned as the ratio of the strati fi cation in the free atmosphere to that in the entrainment zone，is found to be a function of entrainment fl ux ratio（Ae）.This leads to a simple expression of the entrainment rate，in whichAeneeds to be parameterized.According to the results in Liu et al.（2016），Aecan be simply expressed as the ratio of the convective velocity scale in the sheared CBL to that in the shear-free CBL.The parameterization of the convective velocity scale in the sheared CBL is obtained by analytically solving the bulk model with several assumptions and approximations.Results indicate that the entrainment process is in fl uenced by the dynamic e ff ect，the interaction between mean shear and environmental strati fi cation，and one other term that includes the Coriolis e ff ect. These three parameterizations constitute a simple model for predicting the growth rate of a well-developed and sheared CBL. This model is validated by outputs of LESs，and the results show that it performs satisfactorily.Compared with bulk models，this model does not need to solve a set of equations for the CBL.It is more convenient to apply in numerical models.

sheared convective boundary layer，relative strati fi cation parameter，entrainment rate，entrainment fl ux ratio，convective velocity scale

1. Introduction

The depth of the CBL is an important parameter in air pollution and NWP models.In these models，the CBL height is often diagnosed from the critical bulk Richardson number or TKE pro fi le（Skamarock et al.，2008）.These diagnosed CBL heights exhibit large intra-scheme variances（Shin and Hong，2011；Xie et al.，2012；Breuer et al.，2014）.Thus，a proper method to estimate the CBL height is important for numerical models.The growth rate of a CBL is actually the entrainment rate when there is no background vertical velocity.In the 1960s，Ball（1960）and Lilly（1968）proposed a bulk model framework to describe the evolution of the CBL. Since then，the bulk model approach has been widely used to predict the CBL entrainment rate.For a sheared CBL，the results of LESs in Kim et al.（2003）showed that the turbulence in the entrainment zone enhances due to the break of Kelvin—Helmholtz billows at the upper edge of the entrainment zone. As a result，the entrainment process accelerates and the IL deepens.In order to adequately capture the entrainment process in a sheared CBL，at least the fi rst-order model（FOM）is needed（Kim et al.，2006；Conzemius and Fedorovich，2007），and the set of equations for the CBL should be solved.Unfortunately，the bulk model is complex and difficult to apply in numerical models since it includes too many unknown variables.Therefore，it is imperative to develop a simple model for predicting the growth rate of a sheared CBL.

The entrainment rate is associated with the entrainment fl ux ratioAe，which is de fi ned as the ratio of heat fl ux at the CBL top to that at the surface.Kim et al.（2006）proposed a parameterization ofAefor the sheared CBL in the FOM framework.They only considered the sheared CBL under the condition of height-constant geostrophic velocity（GC）. However，the LES results in Conzemius and Fedorovich（2006）indicated that the entrainment process has di ff erent characteristics under the condition of sheared geostrophic velocity with a zero value at the surface（GS）.Following the derivation in Kim et al.（2006），Liu et al.（2016）developed a parameterization ofAefor a well-developed and sheared CBL.This scheme takes into account the buoyancy e ff ect and the shear e ff ect in the surface layer，the mixed layer andthe IL.The shear e ff ect in the IL is represented by local momentum fl uxes and velocity jumps at the CBL top，which is similar to that in Pino and De Arellano（2008）.It still includes many variables and thereby cannot be applied directly. However，if the relations between the entrainment variables（e.g.，the entrainment momentum fl uxes，the potential temperature jump，and the velocity jumps）can be described by external parameters（such as the background strati fi cation，the geostrophic wind gradient，and the surface friction velocity），the parameterizations ofAeand the entrainment rate can be simpli fi ed and become applicable.For this reason，the present study aims to develop a simple model appropriate for predicting the growth rate of the sheared CBL by using external parameters.

The parameterization of the entrainment rate suggested by Sun and Xu（2009）and theAescheme proposed in Liu et al.（2016）are simpli fi ed with some assumptions in this study. The LES outputs obtained in Liu et al.（2016）are used for analysis and evaluation.The paper is organized as follows: Section 2 discusses the theoretical considerations in the FOM framework，and a simpli fi ed parameterization for the entrainment rate is proposed.In section 3，the characteristics of the sheared entrainment are analyzed based on the LES results，and the proposed simple parameterization is veri fi ed using the LES outputs.Conclusions and discussion are given in the fi nal section.

2. Simpli fi cation of the parameterization of entrainment rate

2.1. The CBL structure and de fi nitions of variables

In this study，Θ，UandVrepresent horizontally averaged potential temperature and velocity components，while θ，uandvrepresent the fl uctuation parts of potential temperature and the velocity components.represent horizontally averaged vertical fl uxes of potential temperature and velocity components.γθand γurepresent the vertical gradients of the initial potential temperature and the geostrophic velocity in thex-direction.γθand γuare external parameters，which are assumed to remain unchanged during CBL development.Figure 1 depicts the idealized pro fi les of Θ，UandV，and their fl uxes，in a well-developed sheared CBL.The CBL heighth1is de fi ned as the level at whichreaches its minimum.h0is the fi rst zero-crossing height of thepro fi le.h2is de fi ned as the level toward whichbecomes larger than 10%of its minimum.The layer betweenh1andh2is the inversion layer（IL），in which the idealized Θ increases with height.The IL thickness is Δh21=h2-h1.The layer betweenh0andh2is the entrainment zone，in whichis negative.The entrainment zone thickness is Δh20=h2-h0. Θ1，U1andV1are values of Θ，UandVath1.Θ2，U2andV2are values of Θ，UandVath2.The potential temperature jump is ΔΘ=Θ2-Θ1，and the two components of the velocity jump are ΔU_=U2-U1and ΔV=V2-V1.TheAeis de fi ned asAe=-=h1/h0-1.andare the momentum fl uxes ath1，which are obtained by integratingthe momentum equations from the surface toh2.For further details，please refer to Liu et al.（2016）.

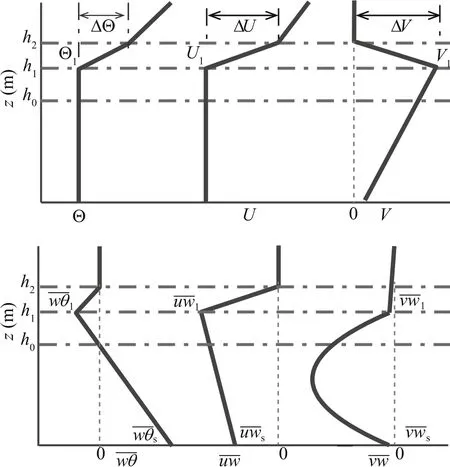
Fig.1.Idealized pro fi les of horizontally averaged potential temperature Θ，velocity componentsUandV，and their vertical fl uxesin the GS cases.Dash-dot lines representh0，h1andh2，and dotted lines represent zero.

2.2. Parameterization of the entrainment rate

In the FOM framework and under the GC condition，the parameterization of the entrainment rate（we）andAeproposed by Kim et al.（2006）and evaluated by Pino et al.（2006）（hereafter KP06）can be expressed as

Following the work of vanZanten et al.（1999），Sun and Wang（2008）derived a parameterization of the entrainment rate for a shear-free CBL，in whichweis normalized byw*and is proportional to the inverse of the convective Richardson number.They argued that their scheme is still valid forthe sheared entrainment process because the scheme is derived from the pro fi les of potential temperature and its fl ux，which have the same shape in both sheared and shear-free CBLs.This argument is supported by the LES outputs for a sheared CBL（Sun and Xu，2009）.The alternative form of Sun and Wang（2008）given in Sun and Xu（2009）is expressed as

where Δh10=h1-h0is the thickness of the lower part of the entrainment zone.As pointed out in Sun and Xu（2009），KP06 and Sun and Wang（2008）are equivalent in describing sheared entrainment，although the expressions are di ff erent.KP06 explicitly includes the e ff ects of shear-produced turbulence，whereas Sun and Wang（2008）uses a geometric relation to implicitly represent the wind shear e ff ects.

In both KP06 and Sun and Wang（2008），the e ff ect of wind shear on the entrainment rate is represented by theAe. It should be noted that Eq.（2）is derived for GC CBLs.A parameterization ofAein a well-developed and sheared CBL is derived in Liu et al.（2016）.The expression reads:

whereVsis the velocity in they-direction at 0.1h1（the top of the surface layer），andis the surface drag coefficient.Note that the geostrophic velocity in they-direction is zero in this study.The coefficients have been determined in Liu et al.（2016），i.e.，A1=0.21，A2=0.01，A3=0.86，andA4=0.70.

The surface drag coefficient in Eq.（5）is not a constant. It is worth noting that an additional term that represents the e ff ect of wind shear in the mixed layer is included in Eq.（5）. In the GC case，Eq.（5）reduces to Eq.（2）.On the other hand，Eq.（5）is the explicit form of Eq.（4）for a sheared CBL.The combination of Eq.（3）and Eq.（5）can be used to predict the evolution of the sheared CBL depth.However，with so many variables in the two equations，they are inconvenient for application.In this study，we attempt to develop a simpli fi ed scheme based on characteristics of sheared entrainment obtained from the LES outputs.

2.3. Simpli fi cation of the parameterization scheme

The relation between ΔΘ/Δh20and γθis often used as a parameter to characterize the thermal structure in the entrainment zone（Deardor ff，1979；Fedorovich，1995；Gentine et al.，2015）.It is called the relative strati fi cation parameter and is de fi ned as

The LES results in Fedorovich et al.（2004）indicate that the dimensionless parameterGis a constant of around 1.2 for shear-free entrainment.Whether it is a constant for sheared entrainment has not been discussed in previous studies.A relationship betweenGandAeis derived from the equation of temperature by order analysis using our LES results（details of the derivation given in Appendix A）.It is expressed as

where the parameterK1is de fi ned asK1=2-Δh21/2Δh20. In order to further simplify the problem，we assume Δh21≈Δh20/2（details aboutGand the validation of the approximation are discussed in the next section）.Thus，K1can be treated as a constant of 7/4，and Eq.（7a）can be written as

Equation（7b）indicates thatGis a function ofAerather than a constant.Substituting Eqs.（6）and（7b）into Eq.（3）and applying the relation Δh20=Δh21+Δh10，we get

In Liu et al.（2016），a new convective velocity scale（wm），which includes the contributions of shear-produced TKE in the whole CBL，is proposed.The results in Liu et al.（2016）indicate thatwmis suitable for characterizing the vertical turbulent motion at the mixed layer top.It is expressed as

Then，Eq.（5）can be rewritten as

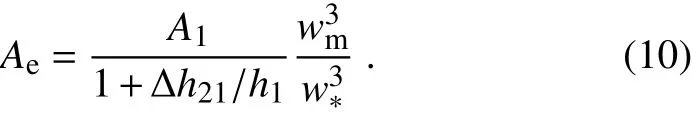
The variation of Δh21/h1is relatively large during the development of a CBL.However，the variation of 1+Δh21/h1is so small（Table 1）that it can be approximately treated as a constant.The LES outputs show that the average value of 1+Δh21/h1is 1.19.Since the value ofA1is set to 0.21（Liu et al.，2016），Eq.（10）is further simpli fi ed to beIt is worth noting that Eq. （11） is not the scheme in the zerothorder jump model （ZOM），although the expression has the same form as that in the ZOM.As shown in Eq.（9），the parameterization is still complex and includes many unknown variables.Thus，how to simplify Eq.（9）is the problem we need to solve.

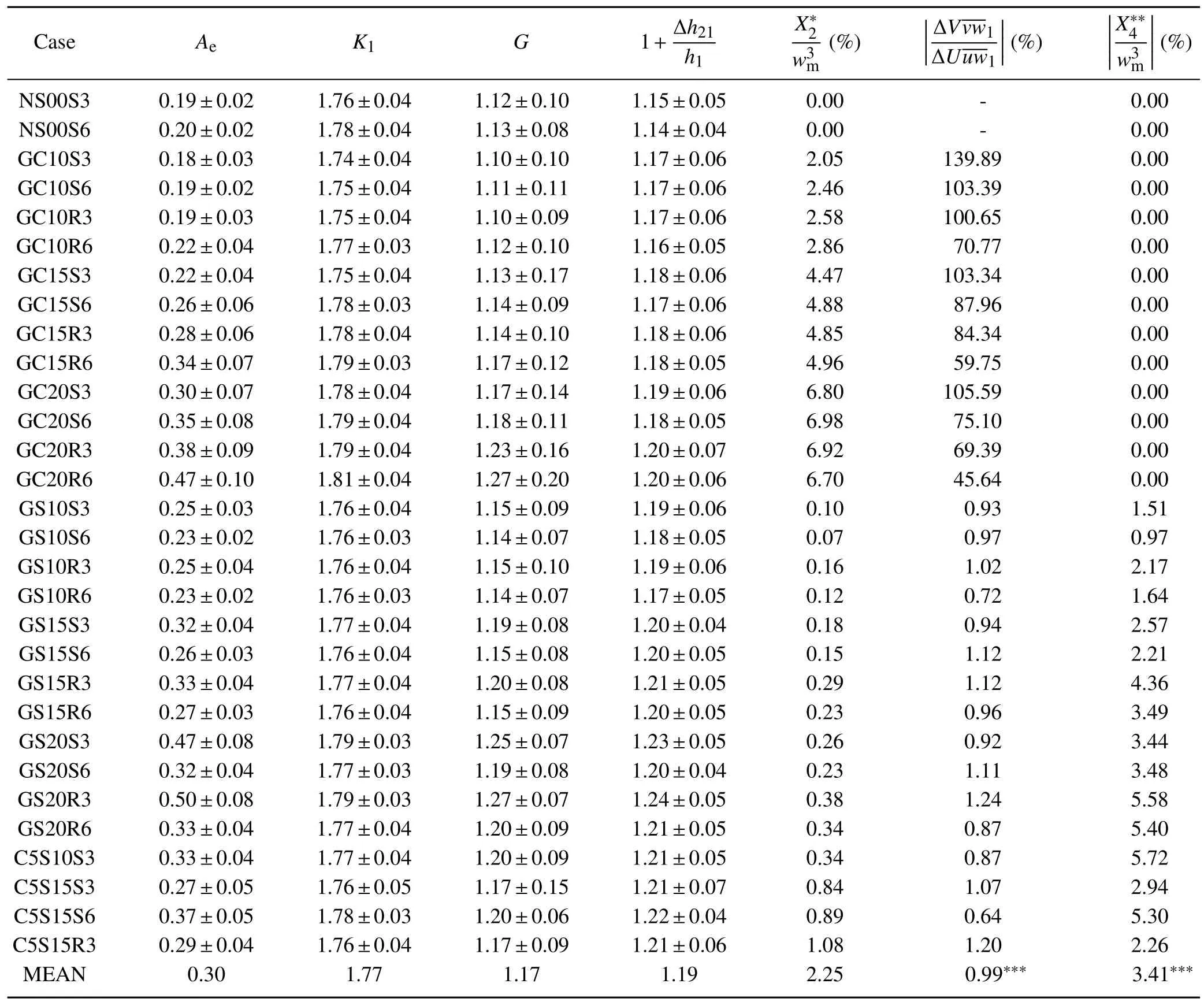
Table 1.Average values of LES data from 4800 s to 28 800 s in the simulated cases.

Liuetal.（2016）showsthatthee ff ectsofwindshearinthe surface layer and mixed layer［the second and fourth terms on the right-hand side of Eq.（5）］on the entrainment fl ux are quite small.Since the terms on the right-hand side of Eq.（9）are proportional to the terms on the right-hand side of Eq.（5），it can be concluded that the second and fourth terms on the right-hand side of Eq.（9）are small when compared with the fi rst and third terms.The ratio of the sum of the second term and the fourth term tois smaller than 5%in most simulated cases（Table 1）.For the purpose of simplicity，the two small terms are neglected in the simpli fi ed parameterization. Therefore，the simpli fi cation of Eq.（9）begins with the third term，hereafter expressed asIn order to derivethe velocity equation is vertically integrated from the surface to the level just above the entrainment zone top.Rearrangement of the integrations yields（see details of derivation in Appendix B）

By using the di ff erential transition，such as∂/∂t=∂/∂h1·∂h1/∂t=（S/h1）∂/∂h1，wherecomesfrom Eq.（8），Eq.（14）becomes

Substituting Eqs.（12）and（13）into Eq.（15），we rearrange the equation to be:

The solution of Eq.（16）can be obtained，in which the coefficients are substituted in for the purpose of simplicity（see details in Appendix C）.It reads:

To solve Eq.（17），we assume that ΔU depends only on h1and 1+Δh21/h1=1.19.Substituting Eq.（17）into Eq.（13）gives a simple expression of.It is written as

where Vg，sand Vg，1are the geostrophic velocity at the surface and CBL top，respectively.

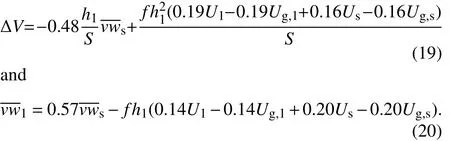
Therefore，in the GC case，the third term in Eq.（9）can be written as（the terms associated with γudiminish because γu=0 in the GC case）

where Ff，GCrepresents the sum of the terms，including the Coriolis parameter（expression not shown）.In order to estimate X3，GC，Eq.（9）with the exact coefficients is written here（the second and fourth terms have been omitted）:

However，for a CBL under the GS condition，V is not constant in the mixed layer，while the shape of theprofi le is di ff erent from that in the GC case.The expressions of ΔV andshould be di ff erent to those in the GC case.The LES results show that，in the GS case，ΔV is far smaller thanΔU，and thus can be neglected（Table 1）.That is，ΔU+ΔV≈ΔU.The LES results also show that， in the GS case，Thereby，X3，GScan be obtained from Eq.（17）and Eq.（18）.It is written as

where Ff，GSrepresents the sum of the terms，including the Coriolis parameter（expression not shown）.When the geostrophic velocity gradient becomes zero（i.e.，γu=0），X3，GSshould reduce to X3，GC.Based on this consideration， we assume that the approximation 0.14（h1/Sis also appropriate for the GS case.Thus，the expression of X3for both the GC and GS cases is

where η is an empirical constant introduced by the above approximations.Replacing S in Eq.（22）by the relation S=［1+（7/4）Ae］/γθ，and further replacing Aeby using Eq.（11），then substituting Eq.（22）into Eq.（9′），we get the following equation:

where a1=4.10η，a2=1.15 and a3=0.57.Since some approximations and assumptions are introduced in the derivation，these coefficients should be adjusted.Multiple linear regression of the LES outputs in the GC and GS cases gives a1=6.02，a2=0.24 and a3=0.86.

Pino and De Arellano（2008）used local momentum fl uxes and velocity jumps to represent the shear production rate of TKE.Equations（17）and（18）indicate that these local quantities are related to surface fl uxes，entrainment rate，CBL height and geostrophic velocity gradient.Equation（22）also indicates that the net shear production rate of TKE in the IL comprises the dynamic e ff ect（second term），the interaction between mean shear and environmental strati fi cation（third term），and one other term that includes the Coriolis e ff ects（ fi rst term）.

Equations（8），（11）and（23）constitute a simple model to predict the height of a sheared CBL.Compared with the KP06 and Sun and Wang（2008）methods，this model doesnot need those variables at the CBL top，such as ΔΘ，Δh21，and so on.Owing to the coarse resolution of NWP and air pollution models，these variables cannot be resolved explicitly（Hong et al.，2006）.Thereby，they must be obtained from a bulk model.However，the input parameters in our simplifi ed model can be easily derived in NWP and air pollution models.andu*can be estimated by a land surface model. γθcan be derived as the mean gradient of potential temperature within a certain thickness（for example，1000 m）aboveh2.γucan be treated as the mean gradient of velocity aboveh2and determined by the same method for the calculation of γθ.In the real atmosphere，the treatment of γumay introduce some errors.However，the CBL’s growth is mainly controlled by surface heating，which explains 70%—90%of this process（Canut et al.，2010；Su¨hring et al.，2014）.This implies that the contribution of entrainment to CBL growth is about 10%—30%.It is expected that the errors induced by γucannot signi fi cantly in fl uence the prediction accuracy.Therefore，this model is more convenient to apply in numerical models.

3. Evaluation and discussion

3.1. LESs

The outputs of the 30 LES runs，described in Liu et al.（2016），are used to verify the parameterizations under the conditions of varying geostrophic wind or wind shear，external strati fi cation，and surface roughness length.The main features of these simulations are described in detail in Liu et al.（2016）.There are two simulations for the shear-free CBL（NS00S3 and NS00S6），while all other simulations are for the sheared CBL and divided into three groups.One group is for CBLs under the GC condition，with vertically uniform geostrophic velocities of 10 m s-1，15 m s-1and 20 m s-1，respectively.The second group is for CBLs under the GS condition，with geostrophic wind gradients of 10 m s-1（2 km）-1，15 m s-1（2 km）-1and 20 m s-1（2 km）-1，respectively，and zero surface geostrophic velocity.In each group under the GC and GS conditions，the simulations are conducted with external temperature gradients of 3 K km-1and 6 K km-1，and surface roughness length values of 0.01 m and 0.1 m，respectively.The name of a simulation case is given according to the simulation conditions.For example，GC20R6 means that the simulation is conducted under conditions ofUg=20 m s-1，a rough surface withz0=0.1 m，and∂Θ/∂z=6 K km-1.In section 2，the derivation of Eq.（23）is based on assumptions and approximations that are obtained from results of the GC and GS cases，and the coefficients are fi tted from simulations of these 24 cases.In order to con fi rm their validity，a third group of simulations are conducted under the CS condition（C5S10S3，C5S15S3，C5S15S6 and C5S15R3）. The CS condition can be regarded as a combination of the GC and GS conditions，in which the geostrophic wind shear exists while the surface geostrophic velocity is not zero.In the four CS cases，the surface geostrophic velocity is 5 m s-1（denoted as C5），while its vertical gradient is 10 m s-1（denoted as S10）or 15 m s-1（denoted as S15）per 2 km，and the meanings of the last two letters in the case names are the same as for the GC and GS cases.The integration covers 28 800 s，and the results from 4800 s to 28 800 s are output at an interval of 100 s for further calculations and analyses.The methods to determine the variables used in calculations and analyses are introduced in Liu et al.（2016）.

3.2. Characteristics of the relativestrati fi cation parameter

According to the de fi nition expressed in Eq.（6），the LES outputs are used to calculate the relative strati fi cation parameterG，and the results are shown in Fig.2（blue dots）.In the GC cases，Ghas a slightly decreasing trend during CBL development.However，the decrease is negligibly small（only about 0.1 in a long period of 24 000 s）.In the GS cases，Galmost does not vary with time.As shown in Table 1，the average value ofGvaries slightly in di ff erent cases.It increases with increasing geostrophic velocity in the GC cases and increasing geostrophic velocity gradient in the GS cases. However，the di ff erence inGamong the simulated cases is very small.The mean value ofGin all of the simulated cases is 1.17（Table 1），which is very close to the result for shearfree CBLs in Fedorovich et al.（2004，thereinG≈1.2）.

The parameterization of the relative strati fi cation parameter，i.e.，Eq.（7a），is derived in the FOM framework.As shown in Appendix A，an approximation is applied to simplify Eq.（A6）.The LES outputs are used to calculate every term on the left-hand side of Eq.（A6），and results indicate that the second and third terms are one order smaller than the other two terms.The LES outputs provide a solid basis for Eq.（7a）.However，Eq.（7a）still includes variables at the CBL top（Δh21and Δh20）.A further simpli fi ed parameterization ofG，Eq.（7b），is obtained by using the assumption of Δh21≈Δh20/2，which may not be true，but the LES outputs show thatK1is almost a constant and approximately equals 7/4（Table 1）.In order to evaluate the performance of Eq.（7b），the LES outputs are used to calculateGaccording to Eq.（7b）.The results are also plotted in Fig.2（red dots）to compare to those calculated according to Eq.（6）［Fig.S1 in electronic supplementary material（ESM）for CS cases］.The spread of LES outputs（especially for GC20 cases when the integration time is longer than 20 000 s）is mainly attributed to the determination method of the upper edge of the entrainment zone，h2，where the instantaneous potential temperature fl ux pro fi le is not equal to zero but fl uctuates around zero. Signi fi cant fl uctuations of Δh21can lead to large fl uctuations of ΔΘ.However，the fl uctuation of Δh20=Δh21+Δh10is relatively small.A small value of ΔΘ always corresponds to a large value ofGcalculated from Eq.（6）.Figure 2 shows that the results from Eq.（6）and Eq.（7b）agree very well in all of the simulation cases，indicating that Eq.（7b）can accurately describe the behavior ofG.

3.3. Evaluation of the CBL height prediction model

Fig.2.Comparison ofG（the relative strati fi cation parameter）calculated from the de fi nition and from the parameterization scheme in the GC and GS cases.The blue dots represent the results from Eq.（6）and the red dots represent the results from Eq.（7b）.

The parameterization of entrainment rate，Eq.（8），is derived from Eq.（3）and Eq.（7b）.Sun and Xu（2009）demonstrated that Eq.（3）works in sheared CBLs.Equation（7b）is validated in the previous section.Thus，we expect thatEq.（8）can predict the CBL height correctly.In order to prove this point，Eq.（8）is solved numerically using the Euler predictor—corrector method over the period from 5700 s to 28 800 s under the CS condition.The time step is 100 s，the same as the time interval of LES outputs.The parameterization schemes ofAeand the convective velocity scale，Eqs.（11）and（23），are used to close Eq.（8）.The LES outputs for the period from 4800 s to 6600 s are averaged to provide the initial condition at 5700 s.Results are illustrated in Figs. 3—5.

Figure 3 shows that Eq.（23）slightly underestimates and overestimateswmat the beginning and end，respectively.This di ff erence is mainly due to the approximation ofand a larger u*gives a larger error. However，thebiasesofestimatedwmareverysmall，makingit reasonable to conclude that the simpli fi ed form of the convective velocity scale Eq.（23）agrees well with its original form，Eq.（9）.Figure 4 shows that theAeestimated by Eq.（11）is in good agreement with that derived from the LESs.As presented in previous studies（e.g.Conzemius and Fedorovich，2006；Pino et al.，2006），the LESAespreads widelybecause it is determined from instantaneous LES pro fi les（calculations show that the spread of LESAeis reduced signi fi cantly when the LES heat fl ux pro fi les are averaged over 500 s）.It is satisfactory that the values of the parameterizedAeare contained within the fl uctuations of the LES outputs.Figure 5 indicates that Eq.（8）can correctly predict the CBL height.

Fedorovich et al.（2004）suggested that，in a shear-free CBL，the CBL √height is proportional to the square root of time，i.e.，h1∝The direct numerical simulations of the CBL driven by a constant momentum fl√ ux in Jonker et al.（2013）yielded the same result，i.e.，h1∝.Our LES results show that this relation also exists in the GC，GS and CS cases（Fig.5 only displays the results in the CS case；see Fig.S2 in ESM for the GC and GS cases）.

3.4. Discussion

The entrainment rate is often parameterized aswe/w*=，whereRi*=（g/Θ0）h1ΔΘ/w2*is the bulk convective Richardson number.In the ZOM，the coefficientAis just theAe.In the FOM，this expression still applies，but the convective Richardson number is di ff erent to that in the ZOM because of the di ff erent de fi nition of ΔΘ.Determination of the coefficientAhas been explored（e.g.，Lewellen and Lewellen，1998；Sullivan et al.，1998；vanZanten et al.，1999；Sun and Wang，2008）.Sun and Wang（2008）gave a relation ofA=（1+Ae）Δh20/h1，indicating thatAis associated with not only theAebut also the entrainment zone thickness and CBL depth.The parameterization scheme for the entrainment rate in Sun and Wang（2008）can be written as Eq.（3）. KP06 provided an equivalent scheme，expressed as Eq.（1）. Both Eq.（1）and Eq.（3）are valid for a sheared CBL，and both imply that the e ff ect of wind shear can be represented by theAe.On the other hand，the two schemes both includethe variable ΔΘ，which is usually unknown.This problem is solved by introducing G.A simple relationship between G and Ae，expressed as Eq.（7b），is derived in this study；and the parameterization of the entrainment rate turns out to be Eq.（8）.

Fig.3.Convective velocity scales calculated from the CBL height prediction model［red line，Eq.（23）］and from LES outputs［blue dots，Eq.（9）］in CS cases.

Fig.4.Aevalues calculated from the CBL height prediction model［red line，Eq.（11）］and from LES outputs［blue dots，Eq.（4）］in CS cases.

For a sheared CBL，the in fl uence of wind shear is included in the Ae.Equation（11）further indicates that the e ff ects of wind shear can be represented by the convective turbulent velocity scale in a sheared CBL，which is always larger than that in a shear-free CBL.Equation（23）gives a parameterization of the convective velocity scale，in which the CBL bulk variables，such as ΔU，ΔV，ΔΘ and Δh21，which cannot be resolved explicitly in most numerical models，are not needed.This is the fundamental di ff erence to the parameterization of KP06.

Actually，Eq.（2）is not the fi nal form of the parameterization of Aein KP06.The fi nal form is expressed as

where Θmis the mean potential temperature in the mixed layerand ΔVeis the velocity jump across the IL.Liu et al.（2016）shows that the value of 1.44 for A3，KPoverestimates the contribution of shear-produced TKE in the IL to entrainment.Our LES outputs are used to optimize the parameters in Eq.（24）.In Kim et al.（2006），ΔVe=0.5（|ΔU|+|ΔV|），and the linear regression yields A1，KP=0.22，A2，KP=-0.54 and A3，KP=2.39.In Pino et al.（2006），，and the linear regression yields A1，KP=0.22，A2，KP=0.23 and A3，KP=0.74.Because A2，KP=（1-α2），A3，KP=2（1-α3），where α2and α3represent the proportions of the dissipation rate to the production rate，and CDis the surface drag coefficient；A2，KPand A3，KPmust be positive and A3，KPmust be less than 2.The negative value of A2，KPand the larger than 2 value of A3，KPimply that the treatment of ΔVein Kim et al.（2006）is not reasonable.In the following calculation，only the ΔVein Pino et al.（2006）is adopted.In order to identify the di ff erences among Sun and Wang（2008），LS（LS is the scheme in this study）and the optimized KP06 schemes，the LES outputs are used to calculate wein the simulated cases，and the relative errors are compared in Fig.6.The relative error is de fi ned as

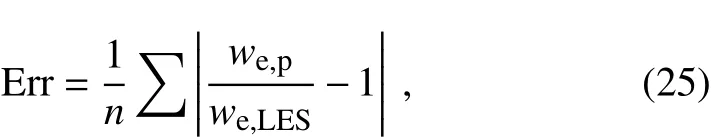
Fig.5.Values of CBL height predicted by the model（red line）and obtained from LES outputs（blue dots）in CS cases. Green squares show the nonlinear fi t of the result of LES CBL height based on the relation that the CBL height is proportional to the square root of time.

where we，pis the predicted entrainment rate，we，LES=∂〈h1〉/∂t，and〈h1〉is the least sq√uares nonlinear fi t of LES h1based upon the relation〈h1〉∝（Fig.5）.In order to understand whether the error of KP06 comes from the parameterization scheme of the entrainment rate［namely，Eq.（1）］or the parameterization scheme of the Ae［i.e.，Eq.（24）］，the errors of the entrainment rate predicted by Eq.（1）and the simplifi ed Aeparameterization scheme［i.e.，Eq.（11）］（denoted as KPLS）are also calculated and shown in Fig.6.Among all the three schemes，the LS scheme performs best，implying that the approximations applied in the derivation of Eq.（23）are reasonable and the derived parameterization can successfully capture the characteristics of the entrainment rate in a sheared CBL.Note that the LS scheme performs better than the Sun and Wang（2008）scheme，although the former is developed on the basis of the latter by using some approximations.The reason is because the spread of instantaneous LES variables（ΔΘ，Δh21，and so on）used in the Sun and Wang（2008）scheme is larger than that of the instantaneous LES variable（namely，h1）used in the LS scheme.KPLSperforms better than the KP06 scheme with optimized parameters but slightly worse than the Sun and Wang（2008）scheme.This suggests that Eq.（1）performs slightly worse than Eq.（3）and the Aeestimated by Eq.（24）has large errors in some cases，even though the parameters have been optimized.The errors of Eq.（24）are partially due to the wide spread of instantaneous LES variables used in Eq.（24）.Based on the above discussion，it is concluded that the assumptions used in the derivations are reasonable and the simpli fi ed parameterizations proposed in this study can correctly predict the Aeand entrainment rate.Meanwhile，the simpli fi ed parameterizations proposed in this study do not include entrainment variables，which may introduce large calculation uncertainties.

4. Concluding remarks

This study aims to simplify the parameterization of the entrainment rate so that it can be conveniently applied to predict the growth rate of a well-developed and sheared CBL. To achieve this goal，G（the relative strati fi cation parameter）is introduced into the parameterization scheme，and the Aeand convective velocity scale in a sheared CBL are simplifi ed according to the characteristics of sheared entrainment，which are derived from the LES outputs.The major fi ndings can be summarized as follows:

（1）G，which is de fi ned in Eq.（6），can be used to characterize the thermal structure in the entrainment zone.Fedorovich et al.（2004）suggested that it is a constant of around 1.2.Theoretical analysis indicates it is a function of the Aeas expressed in Eq.（7b），rather than a constant.This result issupported by the LES outputs.

Fig.6.Relative errors of the entrainment rate predicted by di ff erent schemes against the LES outputs in the simulated cases.

（2）When the relationship between G and the Aeis introduced，the parameterization scheme of the entrainment rate proposed by Sun and Wang（2008）can be rewritten as a simple function of Ae，surface heat fl ux，and the potential temperature gradient in the free atmosphere and the CBL height，as expressed in Eq.（8）.

（3）Shear-produced TKE at the CBL top enhances entrainment.Pino and De Arellano（2008）used the local momentum fl uxes and velocity jumps to parameterize the shear production rate of TKE.Our results show that these local quantities are related to surface momentum fl uxes，the entrainment rate，the geostrophic velocity gradient，the strati fication in the free atmosphere，and the CBL height.The net shear production rate of TKE in the IL is expressed by Eq.（22），which comprises the dynamic e ff ect，the interaction between mean shear and environmental strati fi cation，and one other term that includes the Coriolis e ff ect，and can be approximately characterized by.Based on Eq.（22），the convective velocity scale proposed in Liu et al.（2016）can be further expressed by Eq.（23）.

（4）In the framework of FOM，the IL thickness a ff ects the Ae.The LES outputs show that this e ff ect can be described by a constant，and thus the parameterization of Aeproposed in Liu et al.（2016）is simpli fi ed by Eq.（11）.

（5）The parameterizations of the entrainment rate，Aeand convective velocity scale constitute a prediction model for CBL height.The LES outputs show that it is an appropriate model for a well-developed and sheared CBL.Compared with bulk models，the parameters needed by this model can be easily derived in an NWP or air pollution model.Therefore，this model is more convenient for application.However，the performance in NWP and air pollution simulations needs further validation.

As pointed out in Liu et al.（2016），the parameterizations obtained in this study may only be suitable for welldeveloped CBLs under idealized conditions.The storage term in the TKE budget is ignored in the derivations.However，this term is not negligibly small in the early stage of CBL development.Under this condition，the performance of the simple model needs to be veri fi ed.In this study，the potential temperature gradient in the free atmosphere and the geostrophic velocity gradient are assumed to be constant.For a CBL that is growing through a pre-existing inversion or a residual layer，application of Eq.（7a）becomes problematic，especially when there is a residual layer，because the relative strati fi cation parameter may not exist.How to parameterize the entrainment rate under these conditions needs further investigation.Intherealatmosphere，thegeostrophicwindmay not vary linearly with height.Thereby，the applicability of the simpli fi ed parameterizations under this condition needs more evaluation.As discussed in section 2.3，the simple model developed in this study is convenient to apply in numerical models.Wewillincorporatethisschemeintonumericalmod-els and evaluate its performance under real conditions in future work.

Acknowledgements.This work was sponsored by the National Natural Science Foundation of China（Grant No.40975004）and the State Key Basic Program（973）（Grant No.2013CB430100）. The numerical simulations conducted for this study were performed on the IBM Blade cluster system in the High Performance Computing Center of Nanjing University.The authors thank the anonymous reviewers，whose comments greatly helped to improve the manuscript.

Electronic supplementary material:Supplementary material is available in the online version of this article at http://dx.doi.org/ 10.1007/s00376-016-5209-9.

APPENDIX A

Derivation of Eq.（7a）

As presented in vanZanten et al.（1999）and Kim et al.（2006），by vertically integrating the temperature equation for a sheared CBL from surface toh1，fromh1toh2，and fromh2toh2+ε（ε is in fi nitesimal），and applying the idealized profi les of potential temperature and heat fl ux in the FOM（see Fig.1 or Fig.2 in Liu et al.（2016）），rearrangement of the integrations gives

By using Eq.（6），ΔΘ can be expressed as γθΔh20/G.Thus，∂ΔΘ/∂tcan be written as

By using the geometric relation Δh10=Aeh0=Ae（h1-h10），Δh10can be written asAeh1/（1+Ae），and Eq.（A4）turns out to be

Substituting Eq.（A5）into Eq.（A3）gives

In order to simplify Eq.（A6），each term on the left-hand side is calculated with the LES data.The calculations show that the second and third term are one order smaller than the other two terms and can be neglected.Thus，Eq.（A6）can be approximately written as

From Eqs.（A1），（A2）and（A7），Gcan be solved as

whereK1=2-Δh21/2Δh20.

APPENDIX B

Derivation of Eqs.（12）-（14）

The equation ofUfor a CBL is

Integration of Eq.（B1）from the surface to above the top of the entrainment zone can be separately written as

where ε is in fi nitesimal.By using Leibniz’s rule，the lefthand side of Eq.（B2）becomes

whereUdoes not vary with height from 0 toh1and equalsU1.The right-hand side of Eq.（B2）becomes

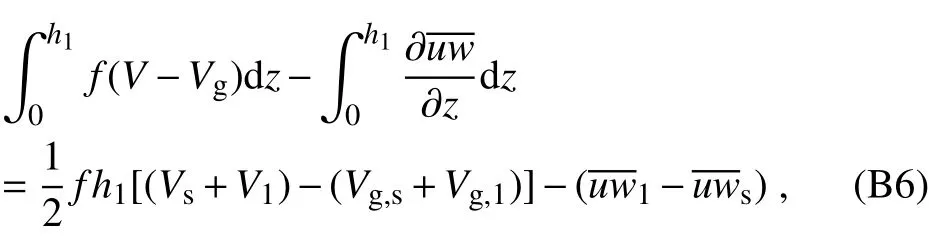
whereVsandV1are the velocity at the surface and CBL top，respectively；andVg，sandVg，1are the geostrophic velocity at the surface and CBL top，respectively.Thus，Eq.（B2）becomes

The above equation is just Eq.（12）.By using Leibniz’s rule，the left-hand side of Eq.（B3）becomes

To derive Eq.（B8），the assumption of∂Δh21/∂t=0 is used，and consequently∂h2/∂tequals∂h1/∂t.The right-hand side of Eq.（B3）can be written as

whereV2，Vg，2andequal zero.Thus，Eq.（B3）becomes

Integrating the left-hand side of Eq.（B4）and using Leibniz’s rule gives

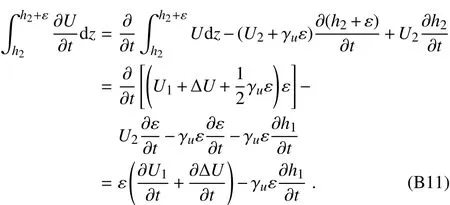
Toderive Eq.（B11），the relationsU2=U1+ΔUand∂h2/∂t=∂h1/∂tare used.It is obvious that the right-hand side of Eq.（B4）equals zero sinceVequalsVganduwequals zero at the height above the entrainment zone.Thus，the right-hand side of Eq.（B11）equals zero，and Eq.（B4）becomes

The above equation is just Eq.（14）.By substituting Eq.（B7）and Eq.（B10）into Eq.（B12）and rearranging the equation，Eq.（13）can be obtained.

APPENDIX C

Derivation of Eq.（17）

The derivation begins with Eq.（16），which is rewritten as

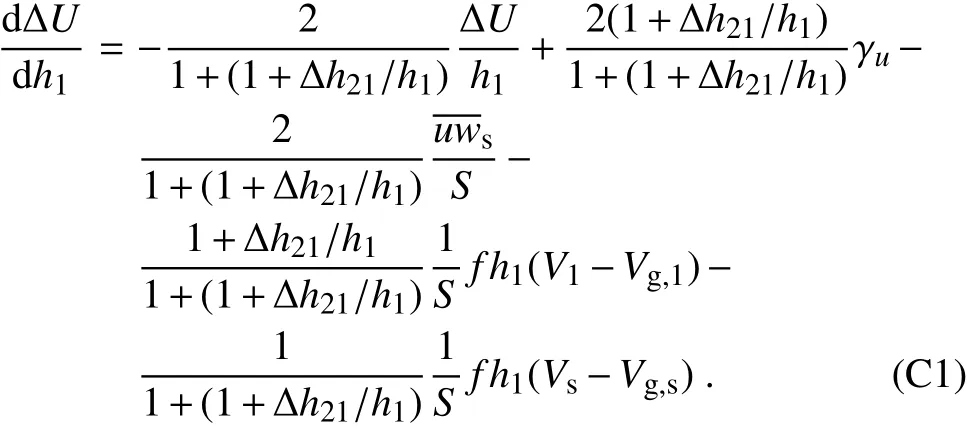
By setting α=1+Δh21/h1and β=1/（1+α），Eq.（C1）be-comes

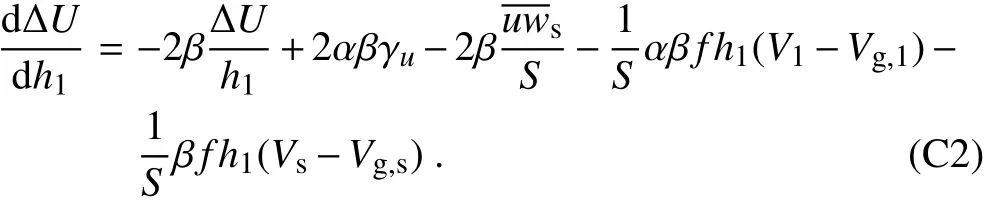
By settinga=2β，b=-αβf（V1-Vg，1）/S-βf（Vs-Vg，s）/S， andc=Eq.（C2）can be written as

Assuming that ΔUdepends only onh1，the solution of Eq.（C3）can be obtained.It reads

Whenh1equals zero，whether ΔUequals zero or not，Eq.（C4）needs Const=0.Thus，Eq.（C4）becomes

Substitutinga，bandcback into Eq.（C5），and，as discussed in section 2.3，using α=1+Δh21/h1≈1.19 to calculate the coefficients，Eq.（C5）turns out to be

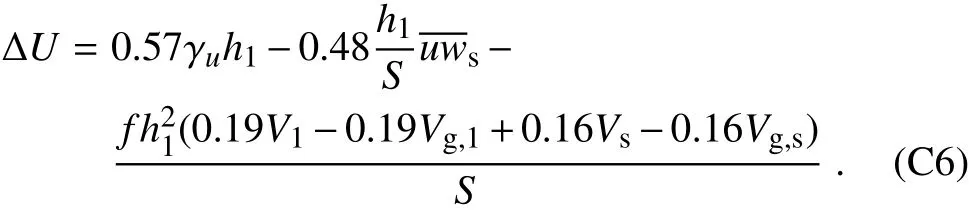
This equation is just Eq.（17）.

REFERENCES

Ball，F.K.，1960:Control of inversion height by surface heating.Quart.J.Roy.Meteor.Soc.，86，483—494.

Breuer，H.，F.´Acs，´A.Horv´ath，P.N´emeth，and K.Rajkai，2014:Diurnal course analysis of the WRF-simulated and observation-based planetary boundary layer height.Adv.Sci. Res.，11，83—88.

Canut，G.，M.Lothon，F.Sa¨ıd，and F.Lohou，2010:Observation of entrainment at the interface between monsoon fl ow and the Saharan Air Layer.Quart.J.Roy.Meteor.Soc.，136，34—46.

Conzemius，R.，and E.Fedorovich，2007:Bulk models of the sheared convective boundary layer:Evaluation through large eddy simulations.J.Atmos.Sci.，64，786—807.

Conzemius，R.J.，and E.Fedorovich，2006:Dynamics of sheared convective boundary layer entrainment.Part II:Evaluation of bulk model predictions of entrainment fl ux.J.Atmos.Sci.，63，1179—1199.

Deardor ff，J.W.，1979:Prediction of convective mixed-layer entrainment for realistic capping inversion structure.J.Atmos. Sci.，36，424—436.

Fedorovich，E.，1995:Modeling the atmospheric convective boundary layer within a zero-order jump approach:An extended theoretical framework.J.Appl.Meteor.，34，1916—1928.

Fedorovich，E.，R.Conzemius，and D.Mironov，2004:Convective entrainment into a shear-free，linearly strati fi ed atmosphere: Bulk models reevaluated through large eddy simulations.J. Atmos.Sci.，61，281—295.

Gentine，P.，G.Bellon，and C.C.Van Heerwaarden，2015:A closer look at boundary layer inversion in large-eddy simulations and bulk models:Buoyancy-driven case.J.Atmos.Sci.，72，728—749.

Hong，S.-Y.，Y.Noh，and J.Dudhia，2006:A new vertical di ff usion package with an explicit treatment of entrainment processes.Mon.Wea.Rev.，134，2318—2341.

Jonker，H.J.J.，M.Van Reeuwijk，P.P.Sullivan，and E.G.Patton，2013:On the scaling of shear-driven entrainment:A DNS study.J.Fluid Mech.，732，150—165.

Kim，S.-W.，S.-U.Park，and C.-H.Moeng，2003:Entrainment processes in the convective boundary layer with varying wind shear.Bound.-Layer Meteor.，108，221—245.

Kim，S.-W.，S.-U.Park，D.Pino，and J.V.-G.De Arellano，2006:Parameterization of Entrainment in a sheared convective boundary layer using a fi rst-order jump model.Bound.-Layer Meteor.，120，455—475.

Lewellen，D.C.，and W.S.Lewellen，1998:Large-eddy boundary layer entrainment.J.Atmos.Sci.，55，2645—2665.

Lilly，D.K.，1968:Models of cloud-topped mixed layers under a strong inversion.Quart.J.Roy.Meteor.Soc.，94，292—309.

Liu，P.，J.Sun，and L.Shen，2016:Parameterization of sheared entrainment in the well-developed convective boundary layer. Part I:Evaluation of the scheme through large-eddy simulations.Adv.Atmos.Sci.，10.1007/s00376-016-5208-x.

Moeng，C.-H.，and P.P.Sullivan，1994:A comparison of shearand buoyancy-driven planetary boundary layer fl ows.J.Atmos.Sci.，51，999—1022.

Pino，D.，and J.V.-G.De Arellano，2008:E ff ects of shear in the convective boundary layer:Analysis of the turbulent kinetic energy budget.Acta Geophysica，56，167—193.

Pino，D.，J.V.-G.De Arellano，and S.-W.Kim，2006:Representing sheared convective boundary layer by zeroth-and fi rstorder-jump mixed-layer models:Large-eddy simulation verifi cation.J.Appl.Meteor.Climatol.，45，1224—1243.

Shin，H.，and S.-Y.Hong，2011:Intercomparison of planetary boundary-layer parametrizations in the WRF model for a single day from CASES-99.Bound.-Layer Meteor.，139，261—281.

Skamarock，W.C.，and Coauthors，2008:A description of the advanced research WRF version 3.NCAR Tech.Note TN-475+STR，77 pp.

Su¨hring，M.，B.Maronga，F.Herbort，and S.Raasch，2014:On the e ff ect of surface heat- fl ux heterogeneities on the mixed-layertop entrainment.Bound.-Layer Meteor.，151，531—556.

Sullivan，P.P.，C.-H.Moeng，B.Stevens，D.H.Lenschow，and S.D. Mayor，1998:Structure of the entrainment zone capping the convective atmospheric boundary layer.J.Atmos.Sci.，55，3042—3064.

Sun，J.N.，and Y.Wang，2008:E ff ect of the entrainment fl ux ratio on the relationship between entrainment rate and convective Richardson number.Bound.-Layer Meteor.，126，237—247.

Sun，J.N.，and Q.J.Xu，2009:Parameterization of sheared convective entrainment in the fi rst-order jump model:Evaluation through large-eddy simulation.Bound.-Layer Meteor.，132，279—288.

vanZanten，M.C.，P.G.Duynkerke，and J.W.M.Cuijpers，1999: Entrainment parameterization in convective boundary layers.J.Atmos.Sci.，56，813—828.

Xie，B.，J.C.H.Fung，A.Chan，and A.Lau，2012:Evaluation of nonlocal and local planetary boundary layer schemes in the WRF model.J.Geophys.Res.，117，D12103.

:Liu，P.，J.N.Sun，and L.D.Shen，2016:Parameterization of sheared entrainment in a well-developed CBL.Part II:A simple model for predicting the growth rate of the CBL.Adv.Atmos.Sci.，33（10），1185—1198，

10.1007/s00376-016-5209-9.

*Corresponding author:Jianning SUN

Email:jnsun@nju.edu.cn