考虑分布式电源最佳接入位置的最大准入容量研究

/西北电力设计院有限公司　王　磊　夏昊君/



技术交流/TECHNICAL EXCHANGE

考虑分布式电源最佳接入位置的最大准入容量研究

/西北电力设计院有限公司王磊夏昊君/

摘要：分布式电源（DG）接入配电网后对节点电压、潮流分布、网损等方面带来的影响与DG的接入位置及容量密切相关。以网损最小为目标函数，针对网络中不同位置的负荷节点对网损的敏感度分析来确定DG的最佳接入位置，进一步以根节点向配电网输出的有功功率最小为目标函数，将电压不越限、网损最小作为约束条件建立了计算DG最大准入容量的数学模型，并采用改进遗传算法（IGA）进行求解。实际算例的仿真结果表明了该算法可以为快速确定DG的最佳接入位置和最大准入容量提供参考决策。

关键词：分布式电源；配电网；最佳接入位置；最大准入容量

0　引言

分布式电源（DG）作为智能电网的重要组成部分，具有减轻环境污染、降低网络有功损耗、改善电能质量等优点［1］。研究表明，DG并网对配电网有很大影响，包括电压水平、网损、可靠性等方面，且其影响程度与DG的安装位置及接入容量密切相关［2-6］。合理的安装位置及接入容量可以有效改善配电网电压质量、减小有功损耗、提高系统可靠性。配置不合理将适得其反，甚至威胁电网的安全稳定运行。因此，为充分发挥DG对配电网的积极影响，在规划阶段应对接入配电网的DG在最佳安装位置与最大准入容量两个方面进行重点研究。

国内外学者从不同角度对DG的最佳安装位置与最大准入容量进行了研究，文献［7］以网损最小为目标，确定了DG的注入容量和接入位置，抽取对线损变化起决定作用的部分网络进行合理的简化等效，分别从DG的注入容量和接入位置两方面对电网线损的影响进行了定量的理论推导，得出了DG注入容量与接入位置之间关系的两个重要公式；文献［8］以分布式光伏电源引起的最大电压上偏差和最大电压波动以及无分布式光伏电源时单纯由负载引起的最大电压下偏差为约束条件，推导出了6种负荷和分布式光伏电源容量沿馈线相同分布条件下能够满足电压质量要求的分布式光伏电源允许接入容量范围；文献［9］讨论了DG优化配置模型，分析推导了配电网中不同位置的负荷节点与网络有功损耗的一般规律，提出了一种DG选址与定容的优化算法；文献［10］建立了以电力公司年综合经济效益最大的优化配置模型，采用改进粒子群算法进行目标函数寻优，最终得到满足目标函数的DG最优配置方案；文献［11］提出了考虑电压调整约束后的准入功率优化计算模型，根据双层优化理论，建立了以准入功率最大化为上层优化目标、满足电压约束为下层优化目标的计算模型；文献［12］建立了负荷和分布式光伏电源引起的电压偏差和电压波动的计算模型，在此基础上定义了分布式光伏电源极端可接入容量极限的概念，即负荷为0的极端情况下不致引起电压偏差和电压波动问题的分布式光伏电源接入容量极限，推导了典型分布情况下线路电压偏差和电压波动不越限时所能允许接入的极端容量极限；文献［13］分析了DG对配电网电压分布和线路潮流的影响以及DG并网位置和功率因数对准入容量的影响，从电力系统静态安全约束的角度出发，建立了计算DG准入容量的数学模型，对于多个DG的情况，提出了准入容量计算的双层优化模型和相应的优化求解算法；文献［14］提出了基于遗传算法求解多个光伏电源同时接入配电网的极限功率的计算方法，该方法考虑了配电网中光伏电源出力突变以及有载调压变压器和并联电容器参与调压的情况，分析了光伏电源接入位置、电网负荷水平以及光伏电源功率因数对极限功率的影响；文献［15］针对DG接入后可能引起电压越限，基于线性化的节点功率方程，提出采用电压灵敏度分析法计算各个节点的DG准入功率。

针对配电网中DG的最佳接入位置和最大准入容量问题，本文研究了配电网中不同位置的负荷节点与网络有功损耗的一般规律，提出了一种确定DG最佳接入位置的算法，同时以根节点向配电网输出的有功功率最小为目标函数，将电压不越限、网损最小作为约束条件建立了计算DG最大准入容量的模型，并采用改进遗传算法（IGA）进行求解。实际算例表明，本文算法是有效可行的。

1　DG最佳接入位置

本文以配电网有功损耗最小作为研究DG最佳接入位置的目标函数［7-9］

式中，f为网损函数；Pi、Qi为支路i末端的有功与无功负荷；Ui为支路i末端的电压；Ri为支路 i 的电阻；n为支路数。

1.1网络中不同节点负荷对网损的影响

假设配电网中仅有节点 i 有负荷，其大小为Pi+Qi，其他节点无负荷时，此时该配电网可以等效如图1所示。

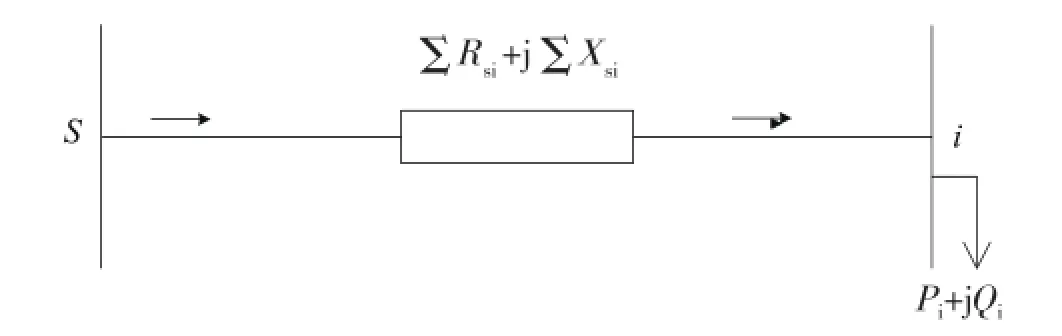
图1　配电网节点i等效图

配电网中其他节点均无负荷，仅由节点i的负荷在整个网络中所引起的有功损耗△Psi为

式中，Pi、Qi分别为节点i的有功负荷、无功负荷；Ui为节点i的电压幅值。

从节点 s 流向节点i的功率为

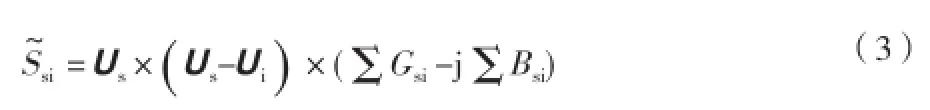
相关研究表明，绝大多数配电网的沿线电压相角变化极小，则

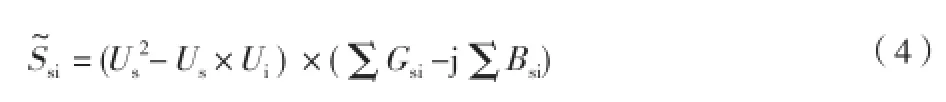
式中，Us、Ui分别为Us、Ui的幅值。

同理，从节点 i 流向节点 s 的功率为

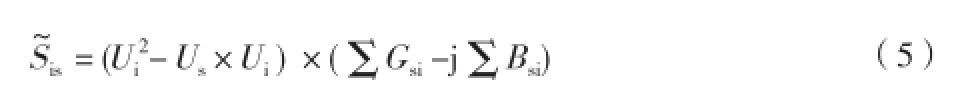
线路的功率损耗为

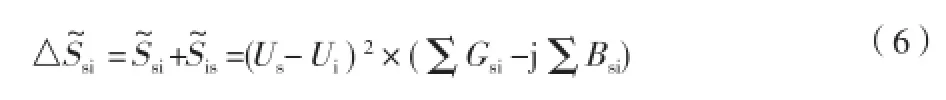
线路的有功功率损耗为

结合式（2）、式（7）可知

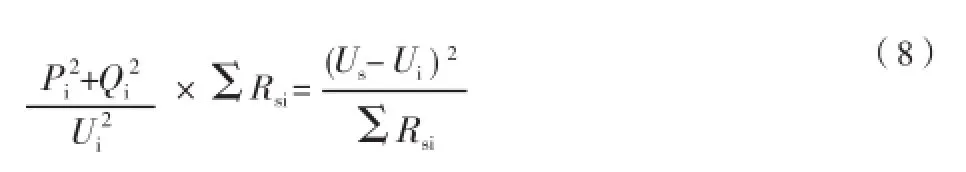
s点的电压可表示为

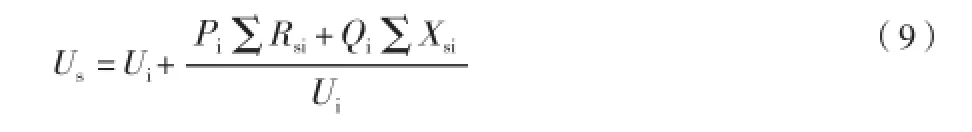
由式（8）、式（9）可知

△Psi可表示为

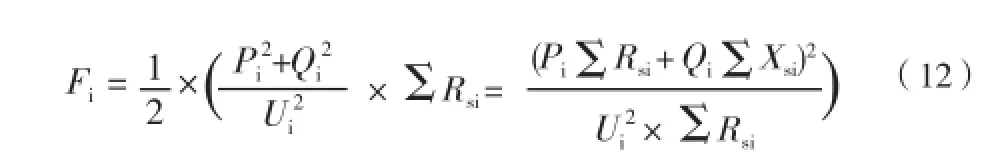
式（12）可理解为：配电网中不同位置的节点 i 对应着不同的和值，即Fi相当于网络中任一节点 i 对网损的函数。

1.2DG最佳接入位置

结合上述分析，同时考虑到有功损耗是由网络中任一节点i的负荷电流流经产生，因此可对式（12）中的求偏导数，此时相当于节点 i 在网络中的位置，即可理解为不同位置的节点对有功网损的敏感度。

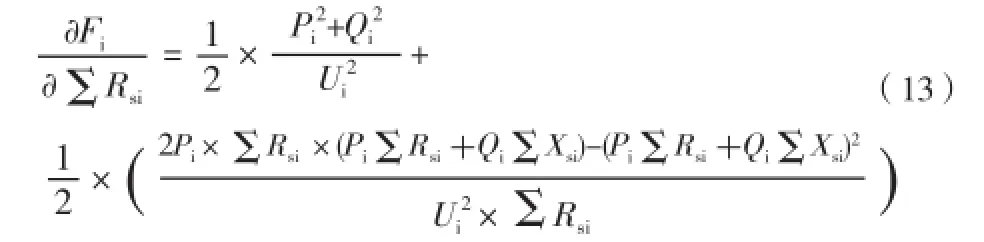
由式（13）可知，欲使节点 i 的负荷电流引起的有功损耗最小，式（13）应满足

式中，Pi定义为节点 i 的负荷电流引起的有功损耗衡量指标。

当式（14）满足时，应有

将式（15）改写为：

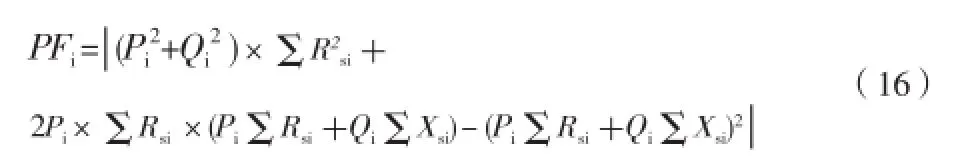
由式（16）可知，节点 i 的 Pi值越接近0其负荷电流所引起的有功损耗越小，反之 Pi值较大的节点其负荷电流所引起的有功损耗越大。

一般情况下，随着配电网络结构的确定，网络中任一节点i的至根节点 s 的和值也相应确定，这是由网络中配电线路的实际参数决定的，无法改变（进行网络重构调整网络结构除外）。而此时能够影响 PFi值的变量就仅有节点 i 的有功负荷Pi和无功负荷Qi，因此，可通过在节点 i 安装DG来起到调整节点 i 的等效负荷从而降低PFi值的作用。

综上可知，应优先在 PFi值较大的节点安装DG。

2　DG最大准入容量

2.1DG并网对配电网电压的影响

DG的接入会影响配电网的潮流分布，从而引起配电网电压变化。单个DG接入配电网的简化电路如图2所示。

图2　单个DG接入配电网的简化电路

图2中，U1为线路首端电压；U2为线路末端电压；R、X分别为线路的电阻和电抗；PL、QL分别为线路末端的有功和无功负荷；PDG、QDG分别为DG的有功和无功输出功率。

DG接入前，线路首端电压U1可表示为

由式（17）可知，没有DG接入的配电网，线路末端电压总是低于线路首端电压。

DG接入后，线路首端电压U1将变化为

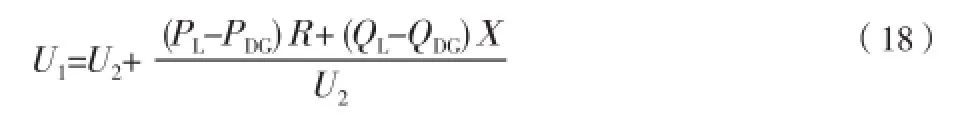
由式（18）可知，DG接入配电网后，将会对配电网的电压产生影响。当DG输出功率过大时，不仅完全平衡接入点负荷，并有盈余功率送入配电网时，此时线路末端电压将有可能高于线路首端电压，严重时甚至可能超过电压允许偏差上限。

2.2DG并网对配电网损耗的影响

DG接入前，线路有功损耗△P可表示为

DG接入后，线路有功损耗△P将变化为

由式（19）、式（20）可知，无论PL与PDG、QL与QDG大小关系如何，△P总大于0。但当DG输出功率过大时，DG接入后线路的有功损耗将有可能反而大于DG接入前线路的有功损耗。

2.3目标函数

根据第2.1节、2.2节分析可知，DG并网将直接对配电网的电压和有功损耗产生影响，具体影响程度与DG的输出功率、线路参数、负荷水平等因素关系密切。在线路参数、负荷水平确定的情况下，DG输出功率过大，将可能导致配电网末端电压升高甚至超过电压允许偏差上限以及有功损耗增加的问题。因此，研究配电网中DG最大准入容量具有重要意义。

DG的最大准入容量目标函数可表示为［16］

式中，P0为根节点向配电网输出的有功功率；PDG、QDG分别为DG的有功和无功输出功率。目标函数表示在正常运行条件下，各个DG最大限度地发出有功功率和无功功率，使P0最小。

2.4潮流计算时DG的处理

考虑到实际情况中，DG一般是安装在负荷的高压母线位置，因此为简化分析，可在仿真计算中DG视为恒功率PQ节点，即假定DG可与负荷就地等效［17］。

当忽略用户变压器损耗等因素，输出功率为 PDG+jQDG的DG接入负荷为 Pi+jQi的母线 i 时，母线 i 的负荷在进行潮流计算时可等效为

3　考虑DG最佳接入位置的最大准入容量

3.1目标函数和约束条件

结合式（1）和式（21），考虑DG最佳接入位置的最大准入容量的目标函数为

式中，△P 为配电网有功损耗。

等约束条件为潮流方程。

不等约束条件如下。

（1）DG无功功率约束

考虑到当前实际DG的制造情况，DG的功率因数cosφ通常在0.85～1之间

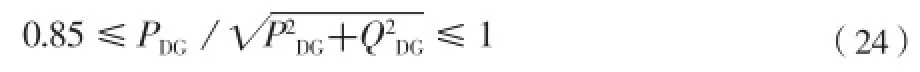
（2）电压偏差约束

由于DG并网改变了配电网的原有潮流分布，因此将会产生电压偏差。一般来说，若电压偏差的允许值较小，是有利于系统正常运行的，但相应的DG的输出功率将被限制；而电压偏差的允许值过大，将会影响电网的安全稳定运行。根据GB/T 12325—2008《电能质量－供电电压偏差》对电压偏差的规定，电压偏差约束为

式中，Ui为节点 i 的电压；UN为系统标称电压；ε1、ε2为国标规定的允许偏差率。

3.2确定DG最佳接入位置

确定DG最佳接入位置的具体流程如下：

1）从根节点开始，计算网络中所有节点（i =1、2、3、…、N）的等值阻抗

2）根据式（16）计算网络中所有节点（i =1、2、3、…、N）的 Pi值；

3）将所有节点的 Pi值按从大到小的顺序进行排列，确定拟安装的DG数量n，前n个节点即为最优安装点。

3.3确定DG最大准入容量

（1）改进遗传算法（IGA）

针对传统遗传算法（GA）在优化过程中计算时间长、收敛速度慢、且易陷入局部最优解的问题，本文采用改进遗传算法（IGA）对DG的最大准入容量进行计算。

（2）染色体编码

以DG输出的有功功率和无功功率为控制变量，将其按一定的组合方式编码成符号串（染色体），每个染色体表示优化问题的一个解。本文采用个体的浮点数编码，个体的染色体编码X可以表示为

式中，N为拟安装的DG数量。Pi的取值范围为0～PL·max（PL·max取值为配电网的有功负荷总和）、Qi的取值范围为0～Qmax（Qmax= Pi×tanφ、cosφ=0.85）。

（3）交叉和变异

式中，α为一随机数，取值范围是［0，1］。

若某一变异点处基因值的范围为 ［ Xmin，Xmax］ ，变异操作就是用该范围内的一个随机数去替换原基因值。

（4）适应度函数

遗传算法在进化过程中需要利用个体的适应度值来进行搜索，适应度值越大的个体对应于更加优化的结果。综合考虑目标函数以及约束条件，同时将问题转化为求最大值，并将式（23）中网损最小的目标函数转换为约束条件（具体表现为在计算DG的最大准入容量时，随着P0的减小、△P也必须同时减小，即不允许出现P0减小△P反而增加的情况），由此建立本文的适应度函数为

式中，A是一个足够大的正常数；k1为网损越限惩罚系数；k2为电压越限惩罚系数；△Pt为正在计算的适应度函数所对应的网损；△Pmin为遗传过程中已计算出的最小网损值。

3.4算法流程

1）输入原始数据，包括配电网的基本参数和遗传算法的操作参数。

2）利用第3.2节所述流程确定DG最佳接入位置。

3）在控制变量约束范围内，初始化种群。

4）设置终止代数tmax，从遗传代数t=1开始，根据种群中不同的染色体各自进行潮流计算以及每个染色体的适应度函数，将其中适应度函数最高的染色体保存为Fbest，并保存对应的染色体。

5）保留当前种群适应度函数最大的前10%的染色体，对其执行选择、交叉和变异操作，再各自进行潮流计算以及每个染色体的适应度函数。

6）对所有染色体的按照其各自的适应度函数进行由大到小的排序，用步骤（5）中保留的10%优良染色体替换当前种群中适应度函数最小的10%的不良染色体，产生新一代种群。

7）将新一代种群中最优染色体的适应度函数值与Fbest进行比较，当其数值大于Fbest时，则将其值重新保存为Fbest，并保存对应的染色体。

8）检查遗传代数t是否等于终止代数tmax，当t=tmax时，算法结束，输出Fbest值及其对应的染色体；否则令t=t+1并返回步骤（5）。

4　算例分析

为验证本文所提算法的可行性和正确性，选择PG&E33标准算例系统［18］进行仿真计算验证。

P G&E 3 3配电网，额定电压为1 2.6 6 k V，总负荷为3715+j2300kVA，共有33个节点（1个根节点、32个PQ节点），37条支路（32条支路、5条联络开关）。拟接入的DG数量为4个，国标规定的允许电压偏差率ε1=ε2=5%，优化参数选取如下：越限惩罚系数k1=k2=2×103，种群大小取100，终止代数取200。

采用本文算法得到的最佳接入位置、最大准入容量如表1所示。

表1　PG&E33系统DG的最佳接入位置和最大准入容量

从表1可以看出，18、25、30、32四个点为DG的最佳接入位置，DG的最大有功输出功率分别为316.86kW、462.42kW、1017.09kW、566.37kW，共2362.74kW；DG的最大无功输出功率分别为196.37kvar、286.59kvar、630.34kvar、351.01kvar，共1464.31kvar。考虑到设备的实际制造情况，18、25、30、32四个点DG的安装容量应分别为400kW、500kW、1100kW、600kW。

表2给出了本文所提算法DG接入前后的潮流计算结果比较。

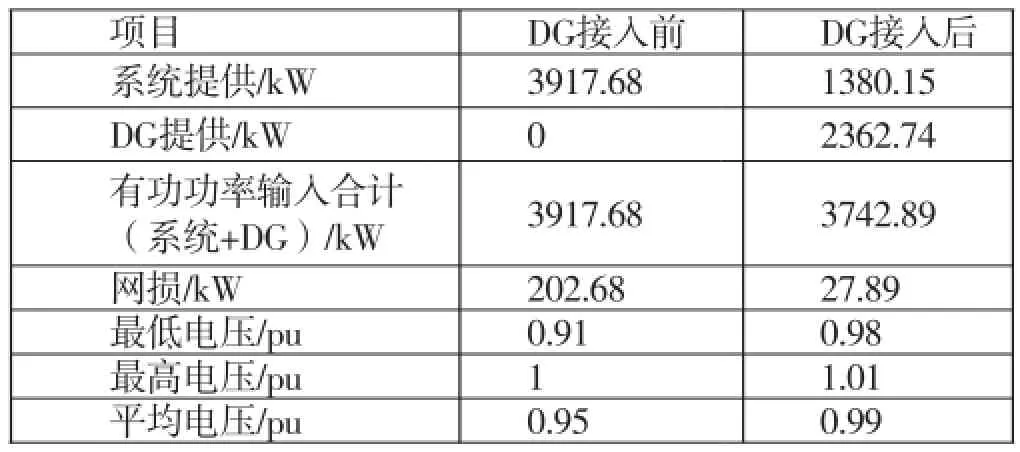
表2　DG接入前后PG&E33系统潮流计算结果比较

从表2可以看出，DG接入后，配电网中各节点的电压升高；此外，DG在向配电网输送有功功率的同时也输送了一定的无功功率。对比各DG的最大准入容量可以看出，负荷较大、较大的节点DG最大准入容量也相对较高。DG接入后平衡节点向配电网输送的有功功率为1380.15kW，说明DG不会向系统输送功率。

从表2还可以看出，DG接入配电网前，为满足负荷供电需求，系统总共需要向配电网提供3917.68kW有功功率，此时对应的整个网络有功损耗为202.68kW；DG接入配电网后，系统和DG总共需要向配电网提供3742.89kW有功功率，此时对应的整个网络有功损耗为27.89kW，相比DG接入前可减少供电/发电侧有功功率输出（即网络有功损耗）174.79kW。可以看出，DG接入对于减少供电/发电侧有功功率输出和网络有功损耗作用明显。

5　结束语

分布式电源（DG）接入配电网后对节点电压、网络潮流、网损等方面将产生影响，具体影响程度与DG的接入位置及容量、线路参数、负荷水平等因素关系密切。

本文以网损最小为目标函数，通过对网络中不同位置的负荷节点对网损的敏感度分析来进行DG选址，敏感度较高的负荷节点引起的网损较大，通过在该节点安装DG对等效负荷予以调整，最后确定网损最小的DG最佳接入位置。进一步以根节点向配电网输出的有功功率最小为目标函数，将电压不越限、网损最小作为约束条件建立了计算DG最大准入容量的数学模型，并采用改进遗传算法（IGA）进行求解。实际算例的仿真结果表明了本文算法可以为快速确定DG的最佳接入位置和最大准入容量提供参考决策。

参考文献：

［1］ 王守相，王慧，蔡声霞. 分布式发电优化配置研究综述［J］. 电力系统自动化，2009，33（18）： 110-115.

［2］ Mendez Q V H， Rivier A J， Gomez S R T. Assessment of energy distribution losses for increasing penetration of distributed generation［J］. IEEE Transactions on Power Systems， 2006， 21（2）： 533-540.

［3］ Lasseter R H. Dynamic distribution using （DER） distributed energy resources［C］ . 2005/2006 IEEE/PES Transmission and Distribution Conference and Exhibition， Dallas， TX， USA， 2006.

［4］ Freitas W， Vieira J C M， Morelato A， et al. Influence of excitation system control modes on the allowable penetration level of distributed synchronous generators［J］. IEEE Transactions on Energy Conversion， 2005， 20（2）：474-480.

［5］Kim T E， Kim J E. Considerations for the operating range of distributed generation interconnected to power distribution system［C］. Proceedings of IEEE PES Summer Meeting， Chicago， IL， USA， 2002.

［6］ 文升，顾洁，程浩忠，等. 分布式电源的准入容量与优化布置的实用方法［J］. 电力自动化设备，2012，32（10）： 109-114.

［7］ 钟嘉庆，叶治格，卢志刚，等. 分布式发电注入容量与接入位置的优化配置分析［J］. 电力系统保护与控制，2012，40（7）：50-55.

［8］ 刘健，黄炜. 分布式光伏电源与负荷分布接近条件下的［J］. 电网技术，2015，39（2）：299-306.

［9］ 庄园，王磊. 分布式电源在配电网络中优化选址与定容的研究［J］. 电力系统保护与控制，2012，40（20）：73-78.

［10］ 贺海，吕娟，王磊. 改进粒子群算法在分布式电源优化配置中的应用研究［J］. 电力科学与工程，2013，29（2）：21-25.

［11］ 胡骅，吴汕，夏翔，等. 考虑电压调整约束的多个分布式电源准入功率计算［J］. 中国电机工程学报，2006，26（19）： 13-19.

［12］ 黄炜，刘健，魏昊 ，等. 分布式光伏电源极端可接入容量极限研究［J］. 电力系统保护与控制，2015，43（3）：22-28.

［13］ 夏成军，崔弘，王强，等. 考虑静态安全约束的分布式电源准入容量计算［J］. 电网技术，2009，33（16）：96-100.

［14］ 丁明，刘盛. 基于遗传算法的多个光伏电源极限功率计算［J］. 电网技术，2013，37（4）：922-926.

［15］ 马越，陈星莺，余昆，等. 基于灵敏度分析法的分布式电源准入功率计算［J］. 电网与清洁能源，2013，29（9）：18-22.

［16］ 苏小玲，韩民晓，赵正奎，等. 配电网中分布式电源最大准入容量分析［J］. 电网技术，2012，36（10）：87-92.

［17］ 陈金富，陈海焱，段献忠. 含大型风电场的电力系统多时段动态优化潮流［J］. 中国电机工程学报，2006，26（3）：31-35.

［18］ 汪兴旺，邱晓燕. 基于改进粒子群算法的配电网分布式电源规划［J］.电力系统保护与控制，2009，37（14）：16-20.