轮廓误差补偿算法研究

高军礼，朱慧华，陈 玮，张小花

(1. 广东工业大学 自动化学院, 广东 广州 510006； 2. 仲恺农业工程学院 自动化学院, 广东 广州 510225)

0 引言

伺服控制技术的高速发展促进数控技术快速发展，尤其在轨迹跟踪控制领域.轮廓误差处理采用两大方案[1]:一种是直接减少轮廓误差，即通过提高单轴的跟踪精度来提高整体的轮廓跟踪精度[1-3]；另一种是间接减少轮廓误差，即通过当前位置得到轮廓误差，解耦补偿各个轴的位置，来直接提高轮廓跟踪精度[4-6].间接减少轮廓误差虽然算法比较复杂，但却是最直接、最快速的补偿算法，其通过当前位置、期望轮廓信息便可以直接对各运动轴实时补偿.

本文以双轴联动系统作为研究载体，以轮廓误差补偿算法为研究对象，分析传统的基于局部任务坐标系的交叉耦合控制算法[7]和最新提出的基于全局任务坐标系算法[8]，对其应用到交叉耦合控制中的理论和仿真进行比较,并对其各自适用场合进行分析.

1 轮廓误差

轮廓误差是指当前位置点与期望轮廓上最近点的垂直距离，如图1所示的Pa1Pc1、Pa2Pc2.间接减少轮廓误差主要采用的控制算法：交叉耦合控制器和基于局部任务坐标系的轮廓运动控制器,解决思路是通过当前点与期望点近似得到轮廓误差之后解耦补偿单轴.另一种是基于全局任务坐标系算法，得到当前运动位置与目标轮廓最近位置的一阶近似值.

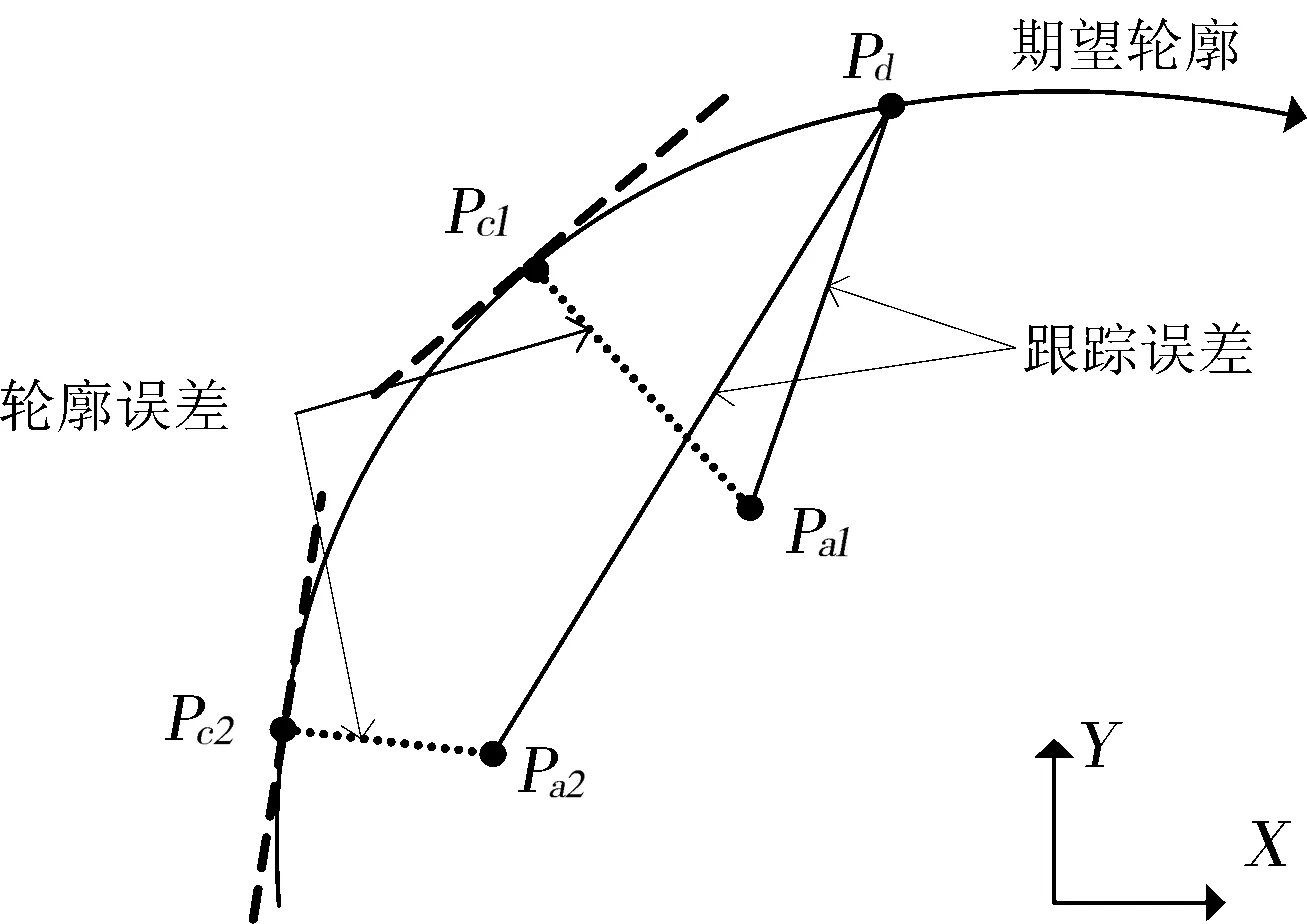
图1 轮廓误差和跟踪误差

2 交叉耦合控制

交叉耦合控制[7]是由Y.Koren以“等位”思想提出来解决双轴进给系统的轮廓运动控制问题，之后Y.Koren等团队又相继提出了变增益交叉耦合控制、轮廓误差传递函数的单变量、任务坐标系的交叉耦合控制等方法[8-9].但这些算法的解决思路都是将实时位置信息反馈给控制器进行计算，近似得出轮廓误差，然后对轮廓误差进行解耦补偿给各个单轴，从而提高轨迹跟踪精度.交叉耦合控制框图如图2所示.

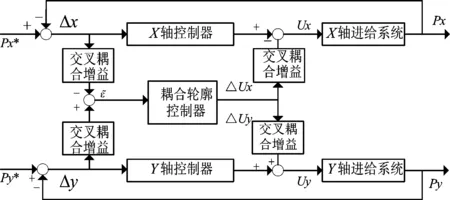
图2 交叉耦合控制框图

假设期望轮廓是一条圆滑轨迹，在某个时刻轨迹跟踪如图3所示.

图3 轮廓误差图

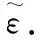
通过建立局部任务坐标系，可得下面推算：

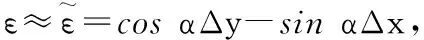
(1)

其中：

Δx=|xd-xa|,Δy=|yd-ya|.

(2)

局部任务坐标系下的交叉耦合控制器只在各轴跟随误差远远小于期望轮廓的曲率半径时，将期望轮廓分段近似为小圆弧的组合.假设轮廓轨迹的中心原点Po(xo,yo)，用ρ来表示参考圆弧的半径，θ为圆弧转动的角度，则近似轮廓误差可以表示为：

(3)

由圆心Po(xo,yo)、实际位置Pa(xa,ya)、期望轮廓位置Pd(xd,yd)，可以得到如下关系

xa=ρsinθ+xo-Δx,ya=-ρcosθ+yo+Δy.

(4)

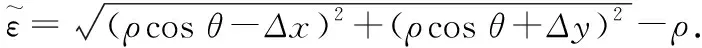
(5)

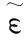
(6)

则交叉耦合增益(Cx,Cy)为

(7)

3 全局任务坐标系

全局任务坐标系是Hu和Yao于1992年在曲线坐标系基础上提出的一种构造正交全局任务坐标系的方法[10].与传统的轮廓误差根据期望位置点与运动目标点近似得轮廓误差不同，其只要求期望轮廓相关的全局任务坐标系算法下的两个任务坐标轴(轮廓误差、运动行程)能够保证在期望轮廓位置上局部正交性.因此可以得到实际运动点能准确地跟踪期望轮廓点，使得实际轨迹与期望轨迹重合，从而提高系统的轨迹跟踪精度，如图4所示.

假设一条光滑的曲线在笛卡尔坐标系(x,y)二维空间中可以表示为：

f(x,y)=0.

(8)

当期望轮廓为光滑曲线时，可构造全局任务空间坐标系r=[rc,rm]T为

rc=f(x,y),rm=g(x,y),

(9)

其中：rc,rm分别表示期望轮廓轴上的法向方向和期望轮廓轴上的切线方向，即rc的值可作为轮廓误差的指标，rm的值期望轮廓上的运动行程.

由期望轮廓曲线坐标可以得到期望轮廓法向的曲线坐标为：

(10)

其中fx=∂f(x,y)/∂x,fy=∂f(x,y)/∂y，可以推导出期望轮廓的法向单位坐标为：

(11)

由式(11)可以得出,曲线坐标rc(x,y)在期望轮廓上的方向和期望轮廓的法向一致，即曲线rc(x,y)在轮廓曲线上值就是实际轮廓误差.

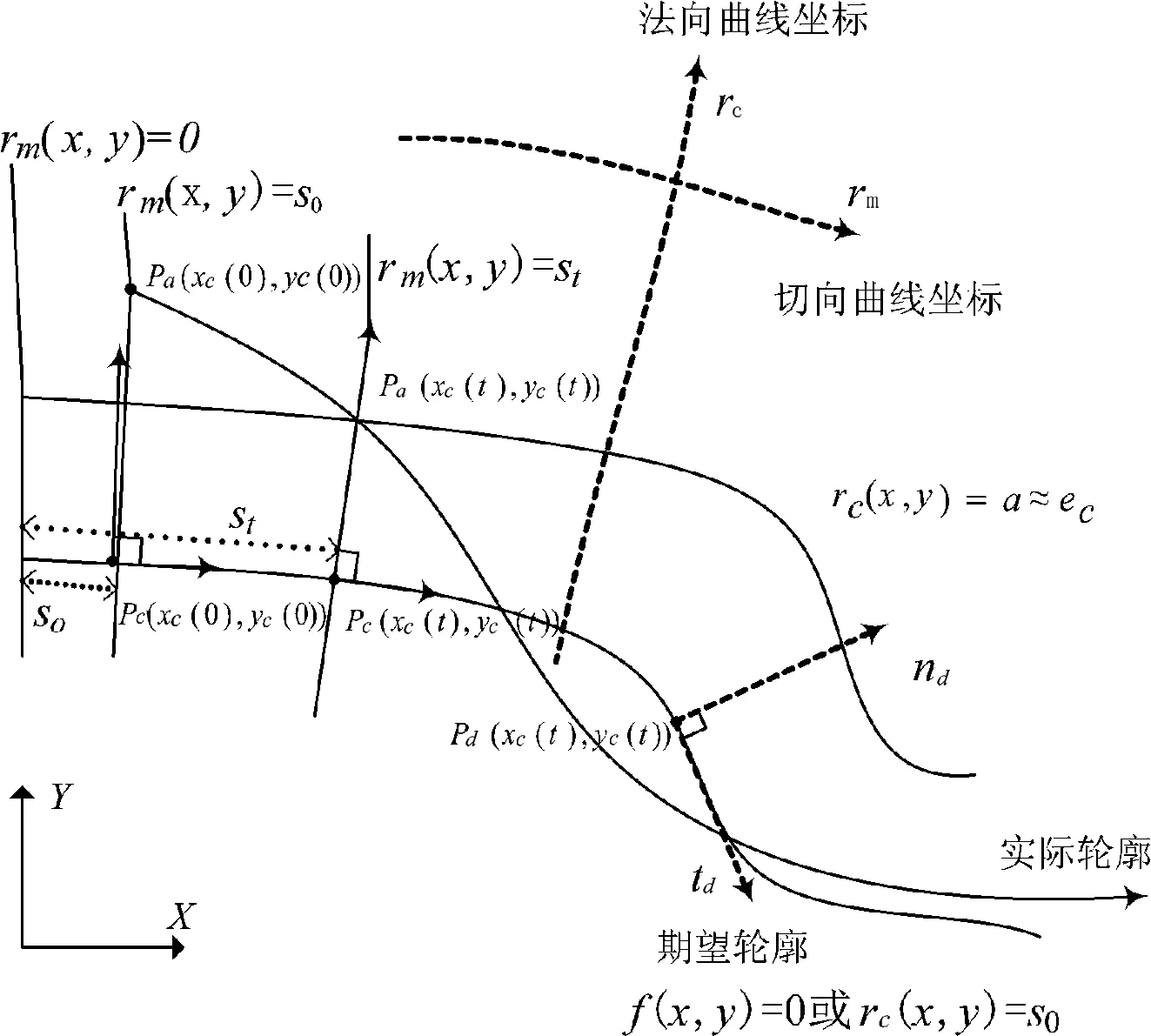
图4 正交全局任务坐标系图

期望轮廓曲线在笛卡尔坐标空间可以由变量ν∈R表示，并且满足下面的两个式子：

qv(v)=[xν(ν),yν(ν)]T,

f(xν(ν),yν(ν))=0,∀ν,

(12)

其中：xν(ν),yν(ν)是分别关于ν的函数，并且存在vx(xv(ν))=ν,∀v.

在笛卡尔坐标空间参数化后，起始点qv(0)沿着期望轮廓到任一点qv(v)之间的行程有下面的积分式子表示：

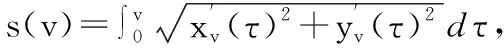
(13)

(14)

则可通过式(14)的方向矢量求得期望轮廓上的单位切向矢量即：

(15)

即通过式(11)和式(15)可知，期望轮廓上的一点对应的轮廓误差rc和运动行程rm方向正交.

4 算法仿真验证

为了验证传统基于局部任务坐标系下的交叉耦合控制算法，将全局任务坐标系算法应用到交叉耦合控制中进行了如下改进与比较.运动控制仿真电机数学模型选用文献[11]，交叉耦合轮廓控制器选用：

交叉耦合控制增益为

假定跟踪的轮廓轨迹为：

(16)

则在全局任务坐标系中根据式(10)可以得轮廓误差rc为：

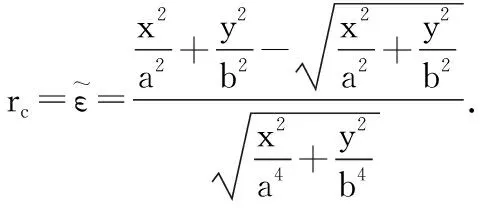
(17)

当a=b时，则跟踪的期望轮廓为圆形轨迹;当a≠b时，则跟踪的期望轮廓为椭圆轨迹;其中Po(xo,yo)代表近似曲线圆点，ω代表曲线的行进速度.在全局任务坐标系中，将采用Matlab里面的m函数方法，计算相应位置的角度信息和对解耦出来的补偿信息补偿到各个单轴.

下面先将a=b，分别选取a=b=1,ω=0.1,Po(1,1)；a=b=10,ω=0.1,Po(10,10)；a=b=10,ω=1,Po(10,10)，得到如下的结果图5所示.

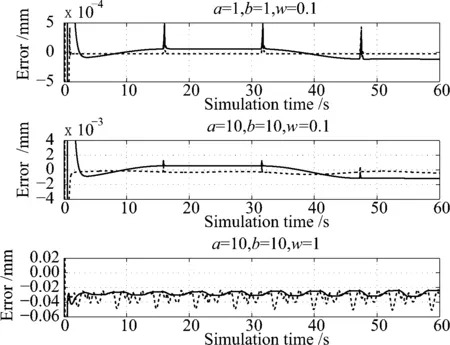
图5 圆轮廓误差对比图

当a≠b时，分别选取a=1,b=0.5,ω=0.1,Po(0.1,0.1)；a=10,b=5,ω=0.1,Po(10,5)；a=10,b=5,ω=1,Po(10,5)，得到如下的结果图6所示.

图6 椭圆轮廓误差对比图

由上面仿真结果图(实线代表全局任务坐标系算法、虚线代表局部任务坐标系算法)可以得出,当期望轮廓为圆形轨迹时，传统的轮廓误差近似算法和全局任务坐标系算法在曲率小并且速率小的情况下，补偿各轴效果基本一致，但局部任务坐标系要优于全局任务坐标系算法;在速率比较大的情况下，全局任务坐标系算法要明显优于传统近似算法的局部任务坐标系算法；而跟踪轮廓为椭圆轮廓时，尤其是在曲率越大,行进速度越快的情况下，基于全局任务坐标系建立的轮廓误差计算方法比传统的交叉耦合控制算法在轮廓补偿效果方面越好.

5 结语

根据传统的交叉耦合控制方法，研究和分析基于局部任务坐标系算法和交叉耦合控制，并将正交全局任务坐标系分析应用到交叉耦合控制器中，验证了全局任务坐标系应用到交叉耦合控制中对期望轮廓特别是曲率大和高速率轨迹跟踪的轮廓补偿具有明显优势.因此，在轮廓误差控制领域中，推广正交全局任务坐标系结合交叉耦合控制补偿算法具有指导意义.